基于三轴加速度信号的心率修正算法

徐 菁 朱 敏

(华东师范大学信息科学技术学院计算中心 上海 200062)

基于三轴加速度信号的心率修正算法

徐 菁 朱 敏*

(华东师范大学信息科学技术学院计算中心 上海 200062)

目前大多数腕带式心率监测设备获得心率的算法主要都是基于光电容积脉搏波描记法PPG(PhotoPlethysmoGraphy)。但是在剧烈运动情况下仅依靠PPG信号获得心率的算法准确度大大降低，并且由于运动伪影MA(Motion Artifacts)的存在大大增加了PPG信号进行频谱分析的难度。为了进一步修正心率检测算法，通过对受测者运动分析，提出一种使用三轴加速度计信号进行修正心率的算法，由运动强度估算出的心率和将PPG信号得到的心率与修正心率通过卡尔曼滤波器处理得到最终心率两部分组成。实验数据记录了由10位受测者以10～16 km/h进行快速跑步的结果，测试数据表明，提出的心率修正算法的绝对平均误差为2.05 BPM。

心率监测 三轴加速度计 卡尔曼滤波器 PPG信号 线性回归模型

0 引 言

心率检测对于运动人群或者是有心脏方面疾病的患者来说具有很重要的作用，目前心率检测的手段主要分为两种：第一种是佩戴心率带，原理是利用心率带上贴在胸口皮肤上的两个感应区块，检测心跳产生的皮肤上的人体生物电变化经过一系列的数值处理得到心率值。此种测量方式是目前最准确的运动心率检测方式，但是由于佩戴舒适度较低的问题使得此种方法并没有推广开来。第二种是佩戴舒适度较高的运动手环，原理是利用PPG血液容积法[11-13]，心脏的周期性波动引起外周血管的周期性收缩与舒张，PPG信号检测装置通过发射绿光照亮皮肤表层，光电传感器接收反射光的强度变化，并通过对PPG信号周期性的检测和分析得到心率值[1-2]。

由于运动过程中PPG信号里存在着大量的运动噪声，通过快速傅里叶算法无法准确的得到心率值，因此提出了大量关于去除运动噪声的PPG信号预处理方法。例如Kim等[3]提出的使用独立变量分析技术(ICA)移除PPG信号里的运动伪影，在他之后Ram等[4]又提出了可以使用自适应噪声消除技术(ANC)去移除运动伪影，这两种方法在运动时对于噪声的移除效果都不太理想。最近Zhang等[5]提出了TROIKA模型，通过对原始PPG信号进行信号分解、稀疏信号重建和谱峰追踪技术来移除运动伪影从而获得心率值。运动伪影移除方法还包括小波去噪[6]，经验模式分解算法EDM(empirical mode decomposition)[7-8]等技术。

在剧烈的运动状态下，PPG信号存在大量无规则的运动噪声，仅仅通过移除运动伪影的方法无法准确地获得心率值得变化。目前大部分的运动手环中都包含三轴加速度传感器，本文提出了利用三轴加速度传感器与PPG信号的结合来获得运动状态下心率的方法。此过程共分为两个主要部分：通过运动强度获得相应心率；利用卡尔曼滤波器得到最终心率。运动强度的增加会导致心率的上升，心率较为缓慢地上升至此时运动强度对应的最大心率。为了克服运动强度的激增与心率的缓慢上升的不平衡性，本文引入了滑动平均滤波器，并且通过50组训练数据得到了较为合理的滑动窗口。

1 问题陈述与动机

在剧烈运动状态下如果将心率监测器佩戴至手腕，那么由于皮肤与检测装置的距离、手腕的复杂运动等因素将产生大量的运动噪声，使得监测器的准确度大大降低。如果只使用PPG信号来获得心率，通常的方法是基于频率分析法[3,5-6]，将三轴加速度的主频通过FFT(快速傅里叶变换)算法算出，并将运动噪声的频率从PPG信号中剔除。最后寻找心率对应的PPG信号中的谱峰，设计一些机制验证所选择的谱峰是否正确。然而用这种算法存在着几个问题。

首先，对PPG信号做频谱分析通常使用快速傅里叶变换，从而得到PPG信号的频率再通过滤波器，将过低和多高的频率给去除掉，但是也会留下过多的噪声频率，而且真实的心率对应频率有可能隐藏在噪声频率的内部。

其次，将PPG信号中的运动噪声去除的过程，有可能把真实的心率对应频率也一并去除，因此会造成检测器的误差。

由此导致在剧烈运动状态下的心率监测器准确度大大降低。剧烈运动会给PPG信号带来大量的运动噪声，然而因为随着运动强度的增减，会导致心率的上升和下降。因此可以进一步研究运动强度与心率之间的关系。

如图1所示。(a)是通过佩戴心率带测得的心率情况，心率带的采样频率为1 Hz。(b)是通过对图(c)中原始运动信号经过滑动平均滤波器处理得到的对应的运动强度，其中采样频率为1 Hz。(c)是通过佩戴运动手环中的三轴加速度计测量得到的x、y、z轴的原始运动信号，原始信号的采样频率为25 Hz。在运动强度有大幅度增加的时候，心率会缓慢增加，随着时间的推移心率会逐渐增加至此时运动强度所对应的心率最大值。可以看出在运动强度开始增加的时候心率并不是立刻增加，而是大约有120 s左右的缓冲时间。在运动过程中，机体会产生一系列的适应性变化。运动时的耗氧量增加，呼吸加快来补充运动时所需要的氧气，而心跳加快能使血液循环加快，使能量输送加快以满足机体临时需要[9-10]。本文提出了一个利用运动强度与心率之间关系的方法，去进一步修正利用PPG信号得到的心率的方法，进一步减小监测器的误差。

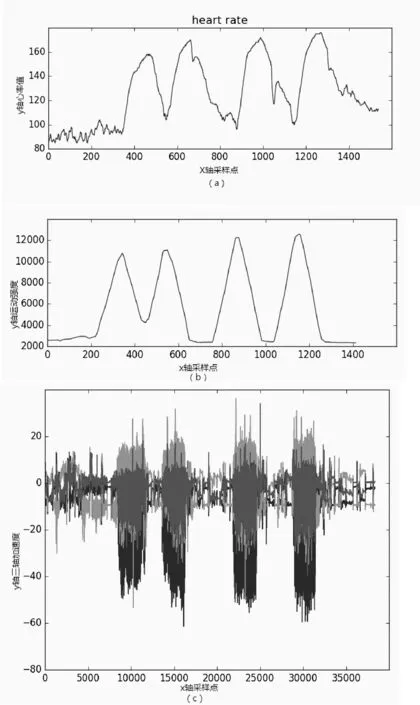
图1 心率和运动强度之间的对应关系

本文提出的心率修正算法，主要包含两个部分：通过三轴加速度计数据计算对应的预估心率值；利用卡尔曼滤波器处理TROIKA框架得到的心率值和预估心率值，从而得到最终心率。

2 心率修正算法实现方法

2.1 数据预处理

在剧烈运动情况下，本文的心率修正算法过程如图2所示，包含：通过运动强度获得相应修正心率、使用卡尔曼滤波器自适应地将PPG信号得到的心率与修正心率以最佳的比例结合。通过PPG信号得到的心率直接使用TROIKA框架[5]即可得到较为准确的心率值。

图2 本文提出的心率修正算法流程图

首先从三轴加速度计得到相应的运动强度，利用三轴加速度传感器采集人体运动加速度并做预处理。以增量为S个采集点的时间窗长为T秒的运动强度(MVL)计算方式如式(1)所示。本文中S=25；T=1；x、y和z代表三轴加速度计采样数据，三轴加速度计的采样频率为25 Hz(用这种处理可以将样本点的频率由25 Hz转变成1 Hz)。

(1)

经过上述滑动平滑处理，已经得到每秒钟的运动强度(MVL)，在运动强度增大的时候，心率会缓慢增加，并随着时间的推移心率会逐渐上升至运动强度对应的最大心率。因此使用滑动平均滤波器处理每秒钟得到的运动强度，使得运动强度与心率之间的数值关系更加明显。本文中滑动平均滤波器的时间窗长为120 s。通过对图1(a)和图3的观察和分析可以看出，在运动强度初步增加的时候心率随之增加，但是随着心率的不断增加，在快到达此时运动强度对应的心率最大值时，心率的增加速率明显减慢。分析结果符合人体学原理，因此考虑运动强度和心率之间在增加的过程中可能属于对数函数关系。图3显示了经过窗长为1 s的滑动平均滤波器处理过的原始三轴加速度信号。图4显示了心率上升段的polar心率带记录的心率值与经过120 s滑动平均滤波器处理过的运动强度之间的散点图。可以看出随着运动强度的变化心率也发生相应的增减变化，虽然每个个体在相同的运动强度下对应的心率最大值可能因为身体素质的差异有所不同，例如男性会普遍高于女性，但是可以准确得到随着运动强度的变化心率的变化趋势。

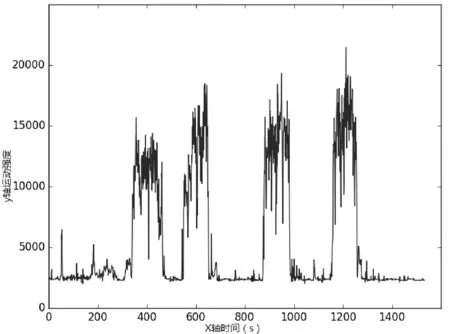
图3 原始加速度信号经过1 s的滑动平均滤波器处理之后得到的三轴加速度平方和

2.2 通过运动强度获得相应心率

观察图4，x轴为心率带测得的心率值，y轴为对应的经过120 s滑动平均滤波器处理过的运动强度——运动积累量。可以明显看出散点图中运动积累量和心率值呈现对数函数的变化趋势。本文采用线性回归模型对散点图进行拟合，从而得出使用运动强度得到心率的对数函数。

图5显示了50组测试数据的心率上升阶段polar心率带记录的心率值与经过120 s滑动平均滤波器处理过的运动强度之间的散点图。其中黑色曲线代表拟合出的对数函数曲线，其中x轴为运动积累量，y轴为对应的心率值。可以明显看出两者有较强的对数函数关系，因此采用线性回归模型得到其线性关系。定义的线性回归模型中代表运动积累量的对数，θ0是回归常数和θ1为回归系数，Y(X)代表通过线性模型预测得到的心率：

Y(X)=θ0+θ1X

(2)

图5 50组测试数据所有心率上升阶段随着运动积累量的对数函数与心率的变化关系

本文所涉及到的线性回归模型的参数估计采用的是普通最小二乘法，定义出n组训练数据的拟合误差平方和J(θ)，其中Y代表对应的真实心率：

(3)

通过最小化误差平方和J(θ)即可得到模型中的回归常数θ0和回归系数θ1：

(4)

通过模型训练可以得到了运动积累量的对数和心率之间的线性关系，并且通过计算线性方程的确定性系数接近于1，表示该线性回归模型的拟合程度较好。

2.3 通过卡尔曼滤波器处理得到最终心率

已经可以通过线性模型利用运动积累量拟合出修正心率，但是包含心率信息最多的应该是PPG信号，假如只使用运动积累量去估算心率，由于个体的差异，将会造成很大误差。因为每个人在相同运动积累量的时候由于身体素质的差异会导致心率变化的不同，但是增长或者下降的趋势几乎都是可以估算出来的。所以应该将PPG信号和运动积累量这两种数据结合共同估算出心率，使其算法的准确率大大提升。因此下面的主要目的是找到通过PPG信号得到的心率值与通过运动积累量估算出的心率值之间的加权因子。为了增加算法的鲁棒性，本文使用卡尔曼滤波器。

卡尔曼滤波器通过计算和更新卡尔曼增益来改变PPG信号得到的心率值与通过运动积累量估算出的心率值之间的加权因子，问题最终会变成最小化代价函数的四个参数的优化过程：

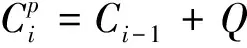
(5)

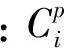
3 实验结果

3.1 实验数据

实验的测试数据有三部分组成：一个单通道的PPG信号、三轴加速度信号、同时记录下来的ECG信号。其中polar心率带得到的心率值是通过ECG信号经过变换处理得出。这三部分数据是在6个男性和4个女性身上测量得到，他们的年龄范围为20～35岁。每一组数据的PPG信号和三轴加速度信号结果都是从手腕部佩戴的运动手环中获得。运动手环中自带脉搏血氧计、LED绿灯和加速度计。而心电图ECG(ElectroCardioGram)信号则是通过胸部佩戴的心率带设备获得。其中PPG信号和三轴加速度记信号的采样频率为25 Hz。

实验记录中的测试者的运动速度为10～16 km/h，并主要记录从静止状态转换为跑步状态的数据。受测人将运动手环佩戴至手腕部。

3.2 算法性能评估

实验将通过每个时间窗内的通过佩戴心率带记录的ECG信号得到的心率值作为真实的心率值。采用多种测量指标来评估使用三轴加速度计信号修正心率算法的性能。BPMtruei表示第i个时间窗内的真实心率值。BPMesti表示第i个时间窗内的使用三轴加速度计信号修正心率算法得到的估算心率值。绝对平均误差被定义为：

(9)

式中：w指的是时间窗的总数。

3.3 实验结果

表1列出了10位受测者分别使用本文提出的心率修正算法和TROIKA心率计算框架的绝对平均误差，TROIKA框架的平均误差为2.97 BPM，而本文提出的心率修正算法的平均误差为2.05 BPM。并且由于此算法运行时空间和时间的消耗也是远小于TROIKA框架，由此可说明该修正算法的必要性和可行性。如图6所示。有三条曲线，分别代表了通过ECG信号(polar心率带)得到的真实心率、TROIKA模型通过PPG信号估算出的心率值和本文提出的心率修正算法得到的心率值。

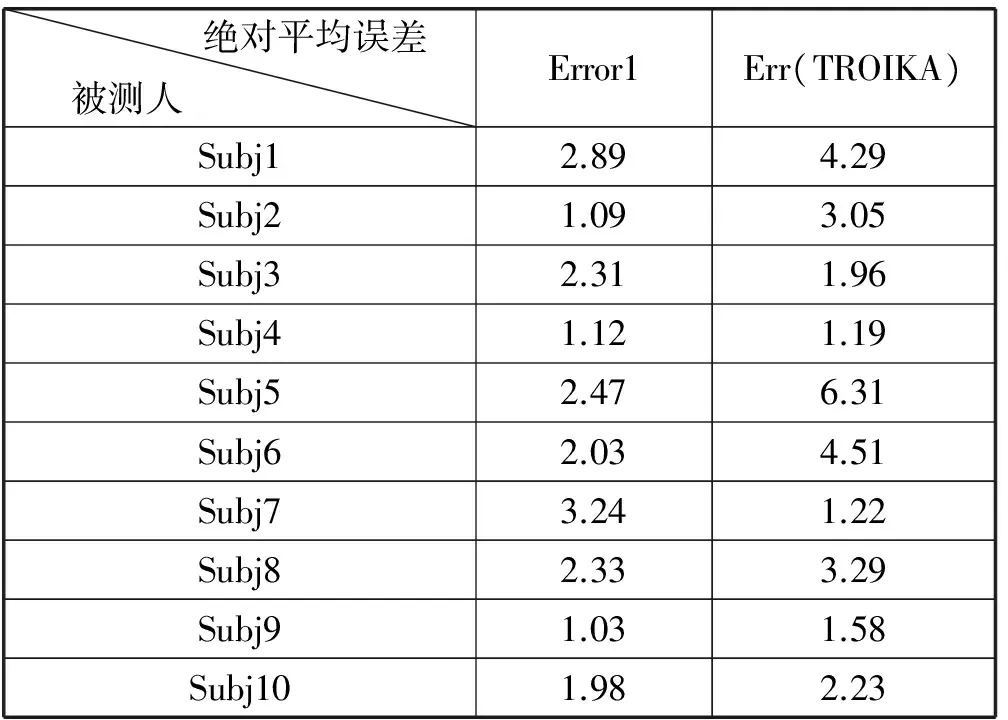
表1 修正算法和TROIKA算法计算出的绝对平均误差

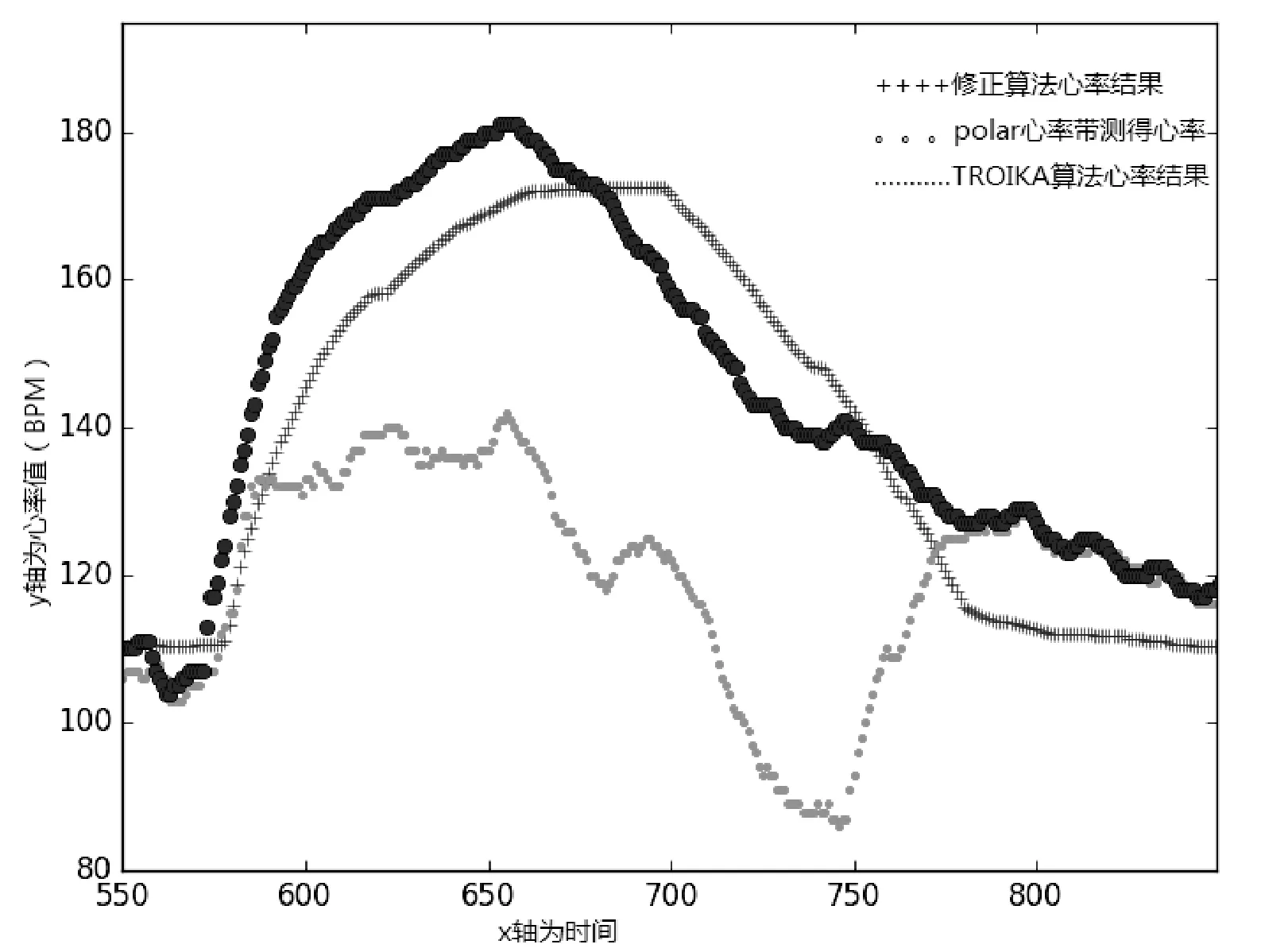
图6 修正算法、polar心率带、TROIKA算法得到的subj5的心率修正结果

4 结 语

本文提出了一种使用三轴加速度计信号去修正心率的算法，可以用来修正从受测者手腕获得的PPG信号估算出的心率值。该算法主要由两个部分组成：使用三轴加速度计信号估算心率，将估算出的心率与PPG信号估算出的心率值通过卡尔曼滤波器进行修正相应比例。实验中的10个被测者得到的数据可以说明此修正算法的准确性。

本文提出的心率修正算法对于只使用PPG信号获得的心率算法有很强的修正性。由于目前市场上绝大多数腕带式运动手环内部的硬件结构都包括三轴加速度计，因此该修正算法对于大部分可佩带运动设备都具有重要的价值。

[1] Hertzman A B,Spealman C R.Observations on the finger volume pulse recorded photoelectrically[J].Am J Physiol,1937,119(334):e5.

[2] Hertzman A B.Photoelectric Plethysmography of the Fingers and Toes in Man[J].Experimental Biology and Medicine,1937,37(3):529-534.

[3] Kim B S,Yoo S K.Motion artifact reduction in photoplethysmography using independent component analysis[J].IEEE Transactions on Biomedical Engineering,2006,53(3):566-568.

[4] Ram M R,Madhav K V,Krishna E H,et al.A Novel Approach for Motion Artifact Reduction in PPG Signals Based on AS-LMS Adaptive Filter[J].IEEE Transactions on Instrumentation & Measurement,2012,61(5):1445-1457.

[5] Zhang Z,Pi Z,Liu B.TROIKA:A General Framework for Heart Rate Monitoring Using Wrist-Type Photoplethysmographic (PPG) Signals During Intensive Physical Exercise[J].IEEE Trans Biomed Eng,2015,62(2):522-31.

[6] Raghuram M,Madhav K V,Krishna E H,et al.Evaluation of wavelets for reduction of motion artifacts in photoplethysmographic signals[C]//International Conference on Information Sciences,Signal Processing and Their Applications,Isspa 2010,Kuala Lumpur,Malaysia,10-13 May.DBLP,2010:460-463.

[7] Sun X,Yang P,Li Y,et al.Robust heart beat detection from photoplethysmography interlaced with motion artifacts based on Empirical Mode Decomposition[C]//Ieee-Embs International Conference on Biomedical and Health Informatics.IEEE,2012:775-778.

[8] Garde A,Karlen W,Dehkordi P,et al.Empirical mode decomposition for respiratory and heart rate estimation from the photoplethysmogram[C]//Computing in Cardiology Conference.IEEE,2014:799-802.

[9] Tulppo M P,Kiviniemi A M,Hautala A J,et al.Physiological background of the loss of fractal heart rate dynamics[J].Circulation,2005,112(3):314-319.

[10] Heffernan K S,Fahs C A,Shinsako K K,et al.Heart rate recovery and heart rate complexity following resistance exercise training and detraining in young men[J].Ajp Heart & Circulatory Physiology,2007,293(5):H3180-6.

[11] Zhang Z.Heart rate monitoring from wrist-type photoplethysmographic (PPG) signals during intensive physical exercise[C]//IEEE Global Conference on Signal and Information Processing.IEEE,2014:698-702.

[12] Zong C,Jafari R.Robust heart rate estimation using wrist-based PPG signals in the presence of intense physical activities[C]//Engineering in Medicine and Biology Society.IEEE,2015:8078-8082.

[13] Mullan P,Kanzler C M,Lorch B,et al.Unobtrusive heart rate estimation during physical exercise using photoplethysmographic and acceleration data[C]//International Conference of the IEEE Engineering in Medicine & Biology Society.Conf Proc IEEE Eng Med Biol Soc,2015:6114.

HEARTRATECORRECTIONALGORITHMBASEDONTHREEAXISACCELERATIONSIGNAL

Xu Jing Zhu Min*

(ComputerCenter,CollegeofInformationScienceandTechnology,EastChinaNormalUniversity,Shanghai200062,China)

Recently, heart rate monitoring using wrist-type PPG (PhotoPlethysmoGraphy) is the main measurement device for the heart rate detection. But it is a difficult problem, since the signals during subjects’ intensive exercise are contaminated by strong motion artifacts caused by subjects’ hand movements. The accuracy of the algorithm based on PPG signal to obtain heart rate is greatly reduced, and the existence of motion artifact increases the difficulty of spectrum analysis of PPG signals. In this study, we propose a modified algorithm for heart rate monitoring based on three-axis accelerometric data, it consists of two key parts, and heart rate estimated by exercise intensity and obtained final heart rate by calman filter. Experimental data recorded the fast running results of ten subjects with 10～16 km/h, and the test data showed the absolute mean error of the proposed heart rate correction algorithm was 2.05 BPM.

Heart rate monitoring Three-axis accelerometric signal Calman filter PPG signal Linear regression model

2017-03-16。徐菁，硕士生，主研领域：信号处理，智能计算与智能系统。朱敏，教授级高级工程师。

TP391

A

10.3969/j.issn.1000-386x.2017.12.055