马尔科夫链蒙特卡洛算法并行化设计与性能分析

周玉科 刘建文 王 妍

1(中国科学院地理科学与资源研究所生态系统网络观测与模拟重点实验室 北京 100101) 2(福州大学空间信息工程研究中心数据挖掘与信息共享教育部重点实验室 福建 福州 350116) 3(中国水利水电科学研究院流域水循环模拟与调控国家重点实验室 北京 100434)

马尔科夫链蒙特卡洛算法并行化设计与性能分析

周玉科1刘建文2王 妍3

1(中国科学院地理科学与资源研究所生态系统网络观测与模拟重点实验室 北京 100101)2(福州大学空间信息工程研究中心数据挖掘与信息共享教育部重点实验室 福建 福州 350116)3(中国水利水电科学研究院流域水循环模拟与调控国家重点实验室 北京 100434)

马尔科夫链蒙特卡洛MCMC(Markov Chain Monte Carlo)算法广泛应用于地球系统模型中参数不确定性分析和模拟。由于地球环境科学数据的高维度、大容量特性，迫切需求高性能的MCMC算法满足应用需求。采用数据分治法实现该算法的多核并行化。利用静态和动态分配策略将算法中的多个输入链分配到各CPU；独立计算并通过共享内存实现进程间通信；主进程回收各单元计算结果，合成最终的马尔可夫链输出矩阵。采用控制变量法分析不同样本和马尔可夫链数量下的算法加速情况。结果表明在计算规模较大、动态负载均衡的条件下易于获得较好的加速比，在4个CPU以内时效果显著，之后随着CPU增加加速效果出现波动或趋于稳定。研究表明并行化MCMC能够利用多核CPU硬件设施获得加速效果，更多核数的加速性能存在进一步优化的空间。

马尔可夫链蒙特卡洛算法 分治法则 多核计算 共享内存 加速性能

0 引 言

在实际生产和科研应用中，经典贝叶斯推断和分析容易受到未知参数后验分布为高维、复杂分布情况的限制，而基于贝叶斯原理的马尔科夫链蒙特卡洛算法MCMC方法能够综合先验和条件信息，并且给出明确的后验信息，可以针对高维积分进行运算。MCMC已经被广泛地应用于统计分析[1-2]、图像处理[3-4]、信号处理[5-6]、金融分析等领域[7]。在地球环境科学领域，MCMC算法主要应用于地球系统模型推断与参数不确定性分析[8-9]、地质化学过程[10-13]等研究。卫星遥感领域，Posselt等利用MCMC算法分析了在劈窗方法下MODIS云数据反演的不确定性[14]。MCMC算法收敛性特征为全局性最小，对应的线性最小二乘法则容易在局部收敛情况下停滞或者由于非线性问题收敛缓慢，同时大量的应用表明 MCMC方法明显优于线性模型[15]。

虽然MCMC算法在理论上容易构建，但在实际操作中比较难以实现[11]，尤其是在地球科学领域数据集通常维度较高，同时大气、海洋、水文等过程模型复杂，这些因素对MCMC的实现也产生严重挑战。因此不断改进MCMC算法的实现模式，增强对地球系统科学数据和模型的适用性是地学领域MCMC算法应用的重要发展方向。随着共享内存式多核计算机的出现，并行计算的格局也从多机集群模式扩展到了单机并行模式，这也使得利用单个高性能计算机实现复杂模型下的MCMC算法成为可能。

MCMC算法输入初始样本和马尔科夫链数量越多，获得的分布函数越逼近于真实的分布函数，因此基于大量样本和马尔科夫链设计分而治之的MCMC算法，充分利用现代高性能计算机的计算能力，有助于提高大规模科研模型和软件的效率，并获得较好的MCMC模拟效果。本文从数据并行的角度出发，根据MCMC算法的特点以马尔科夫链为数据分治对象，将这些对象置于共享内存块中，设计实现多核CPU架构下的并行加速方法。

1 MCMC方法简介

MCMC是贝叶斯推理的标准抽样方法，其是利用Markov链机制探索状态空间以生成样本的方法。通过产生一个待分析概率密度函数为稳定分布的不可分的各态历经的马尔科夫链，并以该链达到稳态的样本作为待分析分布的样本[16]，其重要特性是无后效性，即事物当前状态只与上一状态有关，而与以前状态无关。它突破了传统思维，用相对简单有效的数值方法近似求解贝叶斯推断和分析问题，保持了贝叶斯方法的理论最优性和稳健性。目前MCMC有很多实现算法，如：Metropolis Hastings算法、Gibbs采样等。Metroplis-Hastings(M-H)算法是在概率密度归一化常数(如后验概率中的证据因子)未知条件下的典型MCMC算法，具有适应面广的特点[17-18]。

本文并行化设计方案应用M-H算法(见图1)，其基本思路为：任意选择一个不可约的转移概率q(x,y)以及一个转移概率α(x,y)(0α(x,y)1) ，对任一组合(x,x′)，定义：

p(x,x′)=q(x,x′)α(x,x′)x≠x′

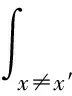
如果链在时刻t处于状态x，即Xt=x，则首先由q(•|x)产生一个潜在的转移x→x′，然后以概率α(x,x′)接受x′作为链下一时刻的状态值，而以概率1-α(x,x′)拒绝转移到x′，从而链在下一时刻仍然处于状态x。

图1 马尔科夫链转移概率示意图

2 MCMC并行化方法

2.1 并行方案

该MCMC多核并行算法遵循分流-合并(Fork-Join)的并行计算模型(图2)，以数据拆分为基础，各计算节点通过共享内存实现参数传递。图2中虚线箭头表示数据到计算节点的流程示意，并非实际的数据分配方案。实线箭头表示算法过程中真实的运算步骤流程。

MCMC并行化过程首先需要进行并行环境初始化，包括检测算法运行平台的可用CPU核数，保证输入多核数量参数不大于可用CPU数量，MCMC标准输入参数的设置(概率函数指针、是否自适应模式、接受率等)。计算环境与算法参数检验通过后进入并行计算过程，输入的马尔科夫链矩阵以行形式存储每条链，根据静态或者动态调度策略，将每行数据分发到各计算单元。实际执行的过程是各计算单元通过内存标记在共享内存中访问对应行的马尔科夫链，然后各子进程独立计算各马尔科夫链。

原始主进程将MCMC概率密度计算表达式分发给各子进程，各计算单元独立计算各自分配的马尔科夫链，最后主进程打开一个管道负责回收各计算单元的计算结果，组合成最终的马尔可夫链矩阵作为MCMC算法输出。其中马尔科夫链的元素按照分布函数随机化生成，因此加载并行程序后还需要初始化随机数序列，为确保每个计算单元采用一致的随机数，主进程将随机数种子发送到各计算单元，初始化时独立产生随机数。

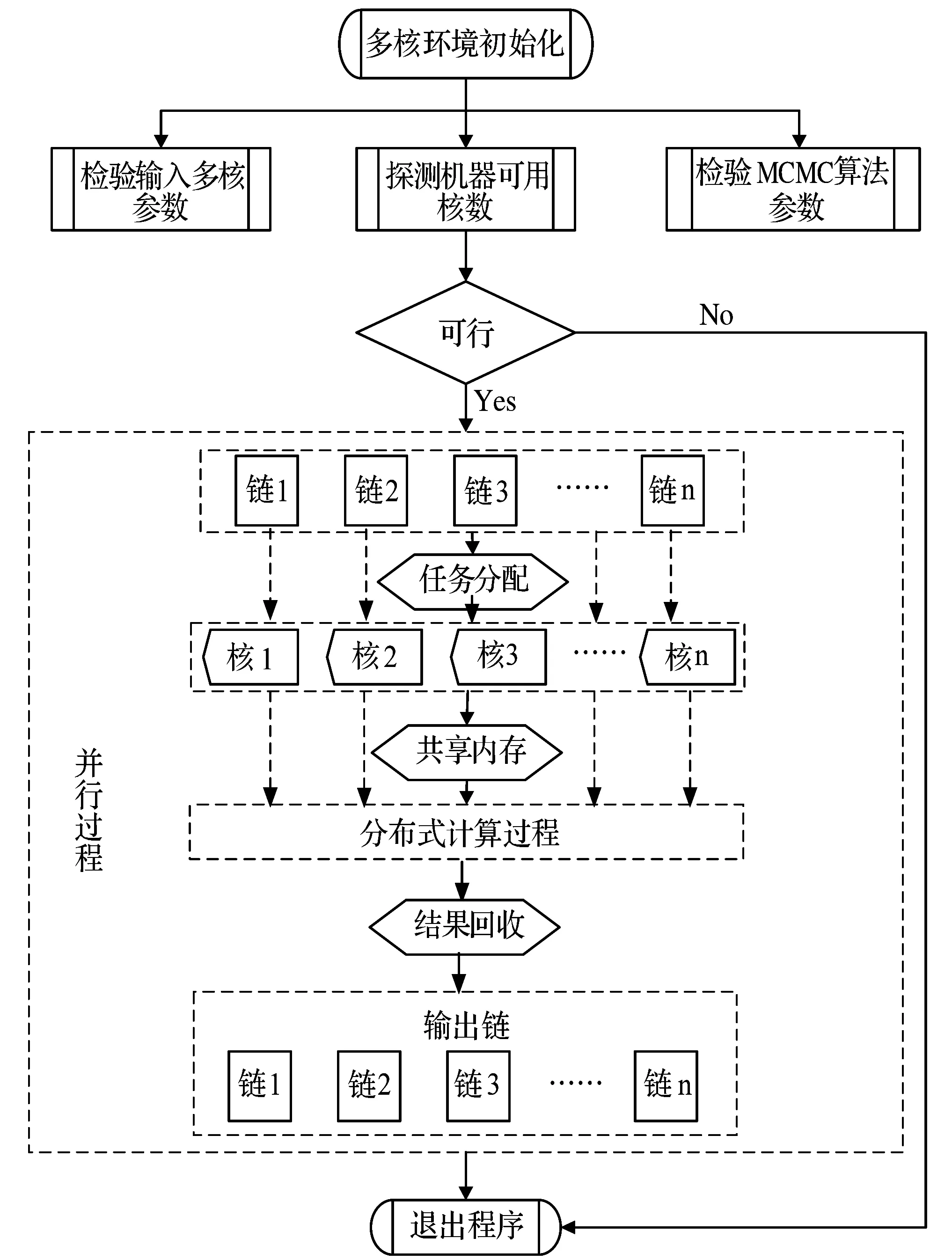
图2 MCMC多核并行计算流程图

2.2 关键技术

2.2.1 概率密度函数分发

本文设计MCMC算法通过构建马尔科夫链从一种banana形式的概率密度分布函数中进行采样，采样中以Log概率密度函数作为MCMC-MH算法中生成样本的来源，Log概率密度函数设置如下(伪代码)：

functionlog．pdf(arrayx){ B<-0．04 -x[1]＾2/200-1/2∗(x[2]+B∗x[1]＾2-100∗B)＾2}

图3为MCMC算法试验的一个串行运行示例，分别采用控制采样数量和自适应模式的方法进行验证。数据的目标分布采用banana形状的概率密度，颜色越红表示分布密度越高，灰色线为等密度线，黑色圈点表示MCMC算法生成样本。从图中可以看出，在采样数量相同的情况下(图3(a)和(b)，图3(c)和(d))，开启自适应模式的MCMC算法生成的结果分布更接近目标分布。比如，无自适应模式的生成样本聚集程度比较高，分布范围相对较小，在某些高密度和边缘区域缺少采样，而自适应模式的采样分布较均匀，覆盖样本区域范围较广。从不同样本数量上分析，增加采样数量不仅能够增加采样密度，而且更加贴近实际分布形状。根据串行运行试验中自适应模式的良好效果，以下的并行版本试验均基于自适应模式进行。

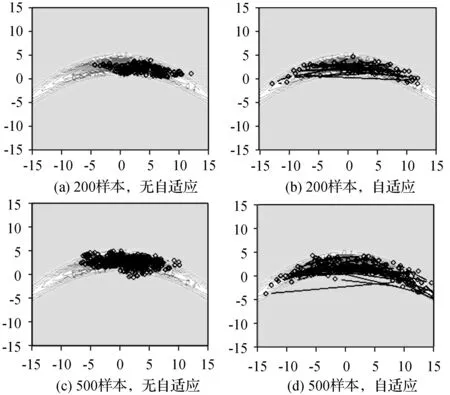
图3 MCMC算法实现示例(不同样本、不同自适应策略)

2.2.2 静态与动态负载均衡策略

本文MCMC并行方法首先采用静态调度策略，主进程根据输入的初始马尔科夫链矩阵行数和设定的CPU核数，将马尔科夫链平均分配到各计算单元进行独立计算，最后主进程收集计算结果。

作为对比和并行优化，同时实现了MCMC多核并行的动态负载均衡策略：如果马尔科夫链的任务队列数量p小于多计算节点(CPU核心)数量n，则计算任务分配个p个计算节点。如果p大于n，那么前n个任务按照顺序依次分配给前n个节点。当某个计算节点第一个任务完成后，该节点成为空闲节点，则第n+1个任务被分配到该节点。按照此顺序一直进行，直到p个任务执行完毕。该策略可以很好地利用集群性能，减少子节点的空转等待时间，但同时也增加了计算节点通信的代价，可能降低并行计算性能。另外，为防止增加更多的计算节点间通信开销，本文方法的负载均衡策略没有设计将指定的任务分配到指定计算节点的方案。

3 性能测试与评价

MCMC多核并行试验使用c语言和OpenMP并行工具库作为开发工具，核心算法采用Metropolis-Hastings算法。实验硬件平台为Dell PowerEdge R720机架服务器，物理8核CPU，主频为2.1 GHz，内存为16 GB，操作系统为Windows Server 2014。实验首先通过控制MCMC算法中关键参数的不同取值，分析其对并行效果的影响；然后在不同的并行调度策略下测试加速效果。

3.1 参数控制并行试验

MCMC 方法依赖于模拟的收敛性，但至今仍没有完全可靠的收敛性诊断方法，这使得收敛性的诊断问题成为MCMC方法实施的难点[4]。为控制不同收敛率带来的并行效果不确定性，本研究MCMC实验均采用相同的收敛率(0.23)。

对于MCMC算法的主要参数配置，并行实验采用1～8个CPU核数递增的测试方案(基于静态调度策略)，对每种CPU核数配置情况进行1 000次模拟实验，取1 000次的平均耗时作为该CPU核数下的并行算法耗时，以降低单次运算带来的误差和不确定性。首先在设定10个马尔科夫链的情况下，采取不同样本数量(1 000，2 000，3 000，4 000个样本)测试并行加速情况，加速时间和加速比结果如图4所示。从加速时间曲线层次排列的情况来看，在相同的CPU核数下样本数量越多运行时间约长。在四种样本数量下试验，运行时间均随着CPU核数的增加而减少，同时可以发现运行时间从1核到3核时急剧减少，此后加速时间微弱减少并趋于平缓，说明在较少CPU核数时加速效果较好，核数量增多加速效果不明显。同时从加速比观察，不同的样本数量加速比呈现多样的波动情况。比如，在3 000和4 000个样本情况下，加速比在5个核数之内呈现显著的上升趋势，之后加速比呈现下降趋势。1 000和2 000个样本下加速比出现波动，加速比在3个核数以后开始下降，而且样本数量越少加速比下降趋势越明显。此部分试验说明增加计算任务量有利于获得更好的加速比，而且可以避免计算任务量不足引起的加速波动。

图4 不同样本数量下的多核并行加速情况

同样在固定样本数量(3 000个)情况下测试多个(6,10,14,18)马尔科夫链的并行加速情况，由图5可以看出加速效果和控制样本数量实验的效果一致。两次试验共同说明增加每个计算单元的任务量有利于持续获取加速效果，但是随着使用CPU核数的增加，各核访问共享内存中数据冲突情况加剧，从而引起加速效果的下降。

图5 不同马尔科夫链情况下的多核并行加速情况

3.2 动态负载均衡的并行实验

在控制马尔科夫链和样本数量两个变量情况下，基于动态调度策略进行实验获取两种情况下(图6(a)和图6(b))的加速情况。在马氏链数量分别设置为6、10、14、18条的情况下，加速时间曲线与静态调度策略下呈现相似的趋势，均是在4个CPU核以内时间减少比较迅速，之后呈现缓慢的降低趋势；从加速比对比分析，在4个CPU核以内加速比与静态策略下基本一致性上升，但是静态策略下4个CPU核以上情况下加速比出现波动现象，并且6和10个马氏链情况下加速比较早出现下降。动态策略下加速比在链数较少和多个CPU核时同样出现下降(如图6(b)在10个链时)，但是整体呈现上升趋势。在MCMC样本数量设置为1 000、2 000、3 000、4 000四种情况下(图7)，动态策略加速时间曲线在小于4个以内CPU核时呈现与静态策略时相似的下降趋势，但是在多于4个核数时波动情况较小，而且仍然有微弱的加速趋势；加速比在多于4个核数时同样比静态调度下波动较少，只是同样的有下降趋势。

图6 动态调度策略下不同马氏链数加速情况

为定量化地比较分析静态调度与动态调度的加速效果，在样本数量和马尔科夫链两个变量控制的基础上，采用动态调度的策略计算运行时间，然后取(Tstatic-Tdynamic)的计算时间差对比分析具体加速效果(图8)。实验结果表明在马尔科夫链数量控制在3 000条的情况下，使用3个CPU核以内时二者的时间差为负数，说明静态调度策略优于动态调度策略，在样本数为2 000时出现个别相反情况。在超过3个CPU核时二者时间差为正数，说明动态调度策略优于静态调度策略。在两种参数控制模式下，3个CPU核内的运行时间差整体小于3个以上情况的时间差，说明计算量是影响调度策略效果的一个重要控制因素。

图7 动态调度策略下不同样本数加速情况

3.3 性能与适用性分析

MCMC算法运行过程中并行部分和非并行部分运行时间不可测度，因此上述试验的运行时间均是算法整体的运行时间。从并行计算的加速效果上分析，MCMC并行实验效果与理想的线性加速比情况相差较远，可以从算法本身特点和并行策略上解释这种差距。首先，MCMC算法的输入马氏链内部的状态矩阵相互依赖性较强，数据的耦合性比较高从而降低了各处理器独立处理数据的几率。后一个矩阵依赖前一个矩阵的状态，因此计算过程存在处理器等待上一次计算结果作为输入的情况。如果某一个状态耗时比较长，会延长整个算法执行时间。其次，分布式计算的各条马氏链特征不尽相同，这种差异也会导致各CPU计算耗时不一致从而引起整体计算时间增加。再次，多核CPU的并行策略是基于共享内存的方式，虽然内存访问效率比较高，但是在大量的并行循环过程中也存在内存访问冲突的情况，多个CPU无法及时地获取输入数据，因此此时并不是并行任务越多利用效率越高的情况。

4 结 语

基于数据分治并行加速的思路，利用多核CPU和共享内存的方法实现了MCMC算法的并行化加速。实验结果表明MCMC算法在不同任务级别下，利用4个以内的CPU核心实现并行化的加速效果比较显著，在4～8个CPU核心上加速效果不明显而且个别案例呈现加速波动情况。采用变量控制法测试了不同MCMC算法参数设置情况下的加速效果，分别控制样本和马氏链数量的实验呈现相似的加速情况，随着样本或者马氏链的增加,运行时间由逐渐增加到趋于平稳。随着CPU核数的增加，加速效果也从逐渐上升到趋于平稳或稍微下降。该分析表明增加MCMC计算规模有利于充分利用多核CPU获得加速效果，由于MCMC算法中马尔科夫链内转移状态的计算过程相互依赖性强(不可并行)，多核并行整体效果跟理想的线性加速比存在一定的差距，但是加速情况已经明显优于串行MCMC算法效率。

[1] Berthelsen K K, Møller J. Likelihood and Non-parametric Bayesian MCMC Inference for Spatial Point Processes Based on Perfect Simulation and Path Sampling[J]. Scandinavian Journal of Statistics, 2003, 30(3): 549-564.

[2] Besag J, Green P J. Spatial statistics and Bayesian computation[J]. Journal of the Royal Statistical Society. Series B (Methodological), 1993,55(1): 25-37.

[3] 成敏,张建州, 于岩. 基于多核的MCMC图像去噪算法并行实现[J]. 计算机工程与应用, 2014, 50(18):152-155.

[4] 李成录,张永仁. 基于贝叶斯与马尔科夫链蒙特卡洛融合算法的图像处理探究[J]. 电子测试, 2013(16): 014.

[5] 靳晓艳,周希元,张琬琳.多径衰落信道中基于自适应 MCMC的调制识别[J]. 北京邮电大学学报, 2014 (1): 31-34.

[6] 李晶,赵拥军,李冬海.基于马尔科夫链蒙特卡罗的时延估计算法[J]. 物理学报, 2014, 63(13): 1-7.

[7] 朱新玲. 马尔科夫链蒙特卡罗方法研究综述[J]. 统计与决策, 2009(21):151-153.

[8] Gallagher K, Charvin K, Nielsen S, et al. Markov chain Monte Carlo (MCMC) sampling methods to determine optimal models, model resolution and model choice for Earth Science problems[J]. Marine and Petroleum Geology, 2009, 26(4): 525-535.

[9] Hassan A E, Bekhit H M, Chapman J B. Using Markov Chain Monte Carlo to quantify parameter uncertainty and its effect on predictions of a groundwater flow model[J]. Environmental Modelling & Software, 2009, 24(6): 749-763.

[10] Korenaga J. A method to estimate the composition of the bulk silicate Earth in the presence of a hidden geochemical reservoir[J]. Geochimica et Cosmochimica Acta, 2009, 73(22): 6952-6964.

[11] Posselt D J. Markov chain Monte Carlo methods: Theory and applications[M]//Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications (Vol. II). Springer Berlin Heidelberg, 2013: 59-87.

[12] 张广智,王丹阳,印兴耀.利用 MCMC 方法估算地震参数[J]. 石油地球物理勘探, 2011, 46(4): 605-609.

[13] 孙海,姚军,张磊,等.基于孔隙结构的页岩渗透率计算方法[J]. 中国石油大学学报: 自然科学版, 2014, 38(2): 92-98.

[14] Posselt D J, L'Ecuyer T S, Stephens G L. Exploring the error characteristics of thin ice cloud property retrievals using a Markov chain Monte Carlo algorithm[J]. Journal of Geophysical Research: Atmospheres, 2008, 113(D24).

[15] Posselt D J, Bishop C H. Nonlinear parameter estimation: Comparison of an ensemble Kalman smoother with a Markov chain Monte Carlo algorithm[J]. Monthly Weather Review, 2012, 140(6): 1957-1974.

[16] Andrieu Christophe, De Freitas Nando, Doucet Amaud, et al. An introduction to MCMC for Machine Learning[J]. Machine Learning, 2003, 50: 5-43.

[17] Metropolis N, Rosenbluth A W, Rosenbluth M N, et al. Equations of state calculations by fast computing machines[J]. Journal of Chemical Physics, 1953, 21: 1087-1091.

[18] Hastings W K. Monte Carlo sampling methods using Markov chains and their Applications [J]. Biometrika, 1970, 57: 97-109.

PARALLELDESIGNANDPERFORMANCEANALYSISOFMARKOVCHAINMONTECARLOALGORITHM

Zhou Yuke1Liu Jianwen2Wang Yan3

1(EcologyObservingNetworkandModelingLaboratory,InstituteofGeographicandNatureResourcesResearch,CAS,Beijing100101,China)2(KeyLaboratoryofSpatialDataMiningandInformationSharingofMinistryofEducation,SpatialInformationResearchCenterofFujianProvince,FuzhouUniversity,Fuzhou, 350116,FujianChina)3(StateKeyLaboratoryofSimulationandRegulationofWaterCycleinRiverBasin,ChinaInstituteofWaterResourcesandHydropowerResearch,Beijing100434,China)

Markov chain Monte Carlo (MCMC) algorithm is widely used in the uncertain analysis and simulation of model parameters in the domain of earth system science. Due to the high dimension and high volume characteristic of earth environment data, it is urgent to develop a high performance version of MCMC algorithm. In this paper, we used the data ‘divide and conquer’ strategy to convert the classic MCMC to a multi-core parallel method. Firstly, the input Markov chains were assigned to multiple CPU cores using static or dynamic load balance plan. Secondly, every standalone core computed the Markov chains assigned by the main process, and the communication between the cores was realized through the sharing memory in the computer. Finally, the main process collected the output Markov chains from every CPU core and aggregated to a Markov chains matrix. The speedup of this parallel MCMC method was tested by selecting different sample size and input Markov chains number. The results indicated that the parallel MCMC got better speedup performance when given more computing task to the CPU cores, as well as using a dynamic load balance

plan when assigned the task to every CPU core. This study showed that parallel version of MCMC method could fully use the hardware of modern computer to obtain acceleration. In our future work, the speedup in the case of more than 4 CPU cores would be further optimized.

MCMC Divide and conquer Multi-core computing Sharing memory Speedup

2017-02-23。国家自然科学基金项目(41601478)；国家重点研发计划项目(2016YFC0500103);中科院STS项目(KFJ-SW-STS-167)；资源与环境信息系统国家重点实际室开放基金项目(2016);中科院地理资源所青年启动基金。周玉科，助理研究员，主研领域：并行空间分析与生态遥感。刘建文，硕士生。王妍，助理研究员。

TP3

A

10.3969/j.issn.1000-386x.2017.12.048