基于Fan模型非负矩阵分解的光谱解混并行计算

江子特 赵辽英 邹佳林

(杭州电子科技大学计算机学院 浙江 杭州 310018)

基于Fan模型非负矩阵分解的光谱解混并行计算

江子特 赵辽英 邹佳林

(杭州电子科技大学计算机学院 浙江 杭州 310018)

基于FAN模型的广义非负矩阵分解是一种非纯像元假设下有效的高光谱图像非线性光谱解混算法。针对基于FAN模型的广义非负矩阵分解算法的快速实现问题，基于CUDA编程模型与存储器模型设计并行优化，对优化后算法的串行与并行部分进行任务分配与线程映射，设计合理的核函数实现各关键步骤。通过真实高光谱数据的光谱解混实验，结果表明CUDA并行优化后的算法相比串行算法，能达到较高的加速比，验证了其有效性。

广义非负矩阵分解 非线性混合模型 并行计算 高光谱图像

0 引 言

高光谱遥感技术以其图谱合一的特点受到国内外的广泛关注，被广泛应用于环境监测、矿产勘察、军事侦察等领域。混合像元的普遍存在是影响高光谱图像实际应用效果的一个重要因素，为此，混合像元分解一直是高光谱图像处理研究的热点。光谱混合从本质上分为线性混合和非线性混合两种[1]，双线性混合模型是非线性光谱解混中用得较多的一类非线性混合模型，包括Fan等提出的Fan模型[2]和Halimi等[3]提出的广义双线性混合模型等。自高光谱遥感出现后，各种线性和非线性的光谱解混技术不断被提出[4-5]，其中非负矩阵分解NMF(Nonlinear matrix fraction)[6]是基于线性混合模型的非监督光谱解混技术的典型代表。由于没有考虑不同端元间的非线性相互作用，NMF不能有效地对非线性光谱混合数据进行光谱解混。针对该问题，文献[7]基于Fan模型提出了称为Fan_NMF的广义NMF算法。

高光谱图像的海量数据使得各种光谱解混算法不能很好地满足高光谱图像的实时应用。由于能够为算法提供接近计算机集群的高计算能力， GPU/CUDA架构已经成为高性能并行高光谱图像处理的一个重要选择[8-9]。罗耀华等[10]提出基于GPU并行实现了高光谱遥感最小噪声分离变换算法，使算法运行速度至少提高了4倍；文献[11]提出了一种基于CUDA的高光谱端元投影向量法的实现方法，使其运算效率提高了十几倍；叶舜[12]研究了基于GPU的稀疏性高光谱图像混合像元分解的并行优化算法，设计了CPU+GPU异构并行计算方法，在Telsa C2050平台上进行实验并取得了14倍的加速比。可见，基于GPU的并行计算可以显著提高高光谱遥感图像的处理效率。

分析Fan_NMF算法过程发现其具有很强的并行性，非常适合GPU加速。本文研究基于CUDA的Fan_NMF并行计算，设计了具体流程和关键步骤的并行计算方法，最后通过实验进行了验证。

1 Fan_NMF 算法

假设R=[r1,…,rN]∈L×N表示高光谱图像数据矩阵，N为像素个数，L为图像的光谱波段数，则rk的Fan光谱混合模型可以形式化表示为:

(1)

式中P为端元个数；M=[m1,m2,…,mP]∈L×P为端元光谱矩阵，sk=[sk1,sk2,…,skP]T∈P中的每个元素ski为该像元中端元mi对应的丰度；ε表示可能的误差或噪声项；⊙表示Hadamard积。

丰度向量sk受到如下两个约束条件的限制：

1≥ski≥0i=1,2,…,P

(2)

(3)

记S=[s1,s2,…,sN]∈P×N，令Mb=[m1⊙m2,…,mP-1⊙mP]∈L×P(P-1)/2，Sb=[s1⊙s2,…,sP-1⊙sP]T∈P(P-1)/2×N，基于Fan_NMF的光谱解混问题可以描述为：给定非负矩阵R,寻找非负矩阵M和S，使得R≈MS+MbSb。

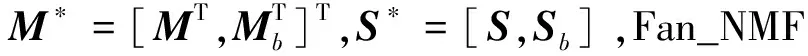
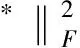
(4)

通过乘性迭代求解目标函数式(4)，得到式(5)和式(6)表示的更新规则：

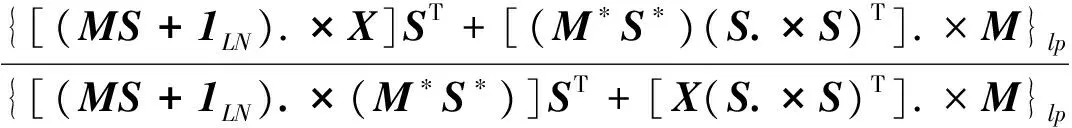
(5)

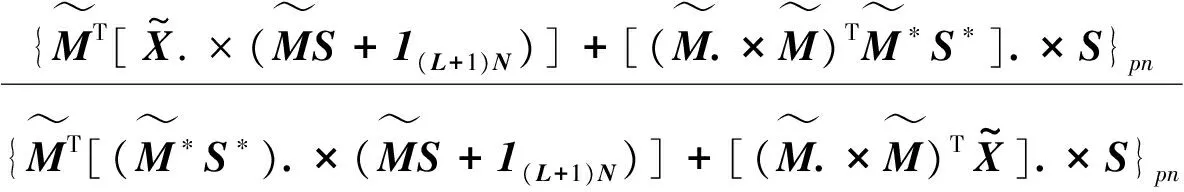
(6)

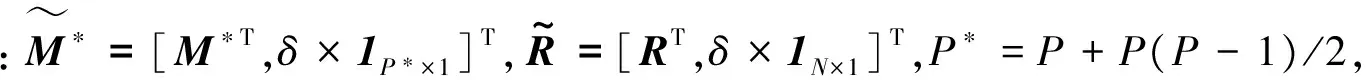
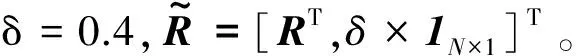
3) 根据式(4)计算目标函数f(M(t),S(t))。

4) 根据式(5)更新M(t+1)，根据式(6)更新S(t+1)。

5)t=t+1，如果t

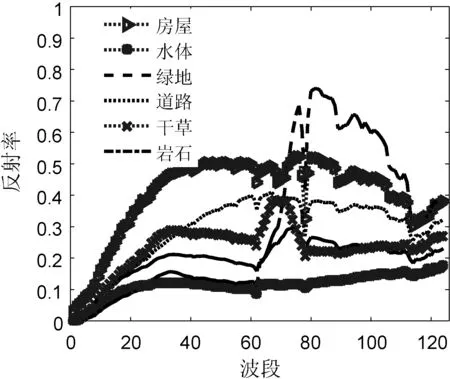
2 基于CUDA的Fan_NMF并行优化

Fan_NMF算法主要运算量在迭代过程，每次迭代要先对端元矩阵和丰度矩阵进行Hardmard积运算，求目标函数，进行端元和丰度矩阵的更新。因此，整个迭代过程由GPU处理，采用CPU+GPU的协同工作达到加速的目的。

并行设计流程图如图1所示。主机端主要负责原始高光谱图像数据的读取操作、初始端元矩阵和丰度矩阵的读取以及端元矩阵及丰度矩阵的主机端存储，设备端则完成算法迭代，最终将计算结果拷贝至主机端。为了简化设计，只以迭代次数满足设定值为迭代结束条件。

图1 基于CUDA架构的FAN_NMF算法结构流程图

下面介绍图1所示的设备端7个步骤的具体设计过程。

Step1端元矩阵M的伪逆计算，利用公式(MTM)-1MT，调用CUBLAS库函数cublasSgemm实现MTM，调用CULA函数culaDeviceSgetrf对MTM进行LU分解，再调用culaDeviceSgetri函数得到(MTM)-1，最后再调用cublasSgemm函数得M的伪逆。各函数启动的线程数量以及每个块的维度依据端元矩阵维度的大小而定。

Step2将高光谱数据及端元矩阵的伪逆作为输入，通过cublasSgemm求解初始丰度，再设计Kernel函数创建N个线程，每个线程计算一个像素的归一化丰度，将结果保存至全局存储器。

Step3以初始端元矩阵为输入，启动点乘Kernel函数，求端元矩阵的Hadamard积。

Step4以丰度矩阵为输入，启动点乘Kernel函数，求丰度矩阵的Hadamard积。

Step5端元矩阵的更新，每个Kenrel启动L×P个线程，具体过程如表1所示。

表1 端元矩阵更新步骤

Step6重复Step3的计算过程，重新计算端元矩阵的Hadamard积。

Step7丰度矩阵更新，每个Kenrel启动L×N个线程，具体过程如表2所示。

表2 丰度矩阵更新步骤

按照Step4-Step7重复迭代，每次迭代结束，迭代次数加1，如果迭代次数大于设定的最大迭代次数，则终止迭代，得到最终的端元矩阵以及丰度矩阵。

3 实验结果及分析

实验数据1：HYDICE采集到的城市高光谱数据集URBAN，如图2(a)所示。图像大小为307×307像素，其包含210个波段。为了提升算法的性能，去除低信噪比和水蒸气吸收波段(1～4，76，87，101～111，136～153和198～210)后剩余162个波段用于本实验，该区域主要包含六种地物：道路、金属、沥青、草地、树木和屋顶。

实验数据2：农作物图，如图2(b)所示，大小为360×550，共124个波段。

图2 真实高光谱图像(第30波段)

实验平台是Windows 7 32位Intel core i5-3580p和NVIDIA GTX 660Ti及CUDA 5.5开发包。实验中用FNSGA方法[14]提取初始端元，全约束最小二乘法[15]求初始丰度。基于CUDA的Fan_NMF并行计算迭代1 000次后，将CUDA处理的实验结果写入txt文件中，通过Matlab显示结果，分别得到图3和图4所示的光谱曲线和图5和图6的丰度图。从图5和图6，可以看出所求的各种地物的分布与图2的目视效果基本一致。

图3 URBAN图端元光谱曲线

图4 农作物图端元光谱曲线

图5 URBAN图的丰度图

图6 农作物图的丰度图

最大迭代次数设置为1 000次时，两幅真实高光谱图像基于CPU和GPU实现Fan_NMF解混的时间比较如表3所示，其中，所有GPU耗时不考虑I/O数据传输以及图像数据的初始化时间，CPU耗时不包括读取图像数据时间。设高光谱图像数据大小为height×width，设置gridDim为[(width+15)/16]× [(height+15)/16]，blockDim(线程块维度)为16，即线程块的大小为256。从表3中可以看出，基于CUDA的并行Fan_NMF算法相比于基于串行CPU实现的Fan_NMF算法性能大幅的提升。基于CUDA的并行Fan_NMF算法处理农作物crops高光谱图像数据时的加速比达到了54.72倍，对URBAN图像进行并行处理加速比为80.96倍。

表3 GPU和CPU运行时间比较

表4给出了基于CUDA并行计算中各部分耗时。从表4中可以看出，在Fan_NMF算法并行实现中，端元及丰度更新操作因为其计算量大，所以占用了相当

部分的并行处理时间，端元扩展以及丰度扩展在计算中耗费的处理时间相对较少，各个Kernel之间进行数据传输也耗费了相当部分的时间，对不同步骤的耗时分析可进一步找出性能优化点。

表4 CUDA实现Fan_NMF算法中各部分耗时 s

4 结 语

本文实现了基于CUDA的Fan_NMF算法并行计算，除了添加虚拟波段操作在主机端Host完成外，其余计算都在设备端完成，减少了主机端与设备端之间的数据交互。在Windows 7 32位的Intel core i5-3580p，NVIDIA GeForce GTX 660Ti实验平台对两幅真实高光谱图像进行Fan_NMF光谱解混，分别取得了54.72倍和80.96倍的加速比。这充分证明了GPU并行计算针对数据量大的高光谱数据解混的优势。本文方法在实现上仍然存在一定的加速空间，例如可以使用共享存储器来提高数据存取效率从而提高加速比。因此，后续工作中还需进一步对程序进行存储器方面的优化。

[1] 童庆禧,张兵,郑兰芬.高光谱遥感——原理、技术与应用[M].北京:高等教育出版社,2006:38-44.

[2] Fan W,Hu B,Miller J,et al.Comparative study between a new nonlinear model and common linear model for analysing laboratory simulated forest hyperspectral data[J].International Journal of Remote Sensing,2009,30(11):2951-2962.

[3] Halimi A,Altmann Y,Dobigeon N,et al.Nonlinear unmixing of hyperspectral images using a generalized bilinear model[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(11):4153-4162.

[4] Bioucas-Dias J M,Plaza A,Dobigeon N,et al.Hyperspectral Unmixing Overview:Geometrical,Statistical,and Sparse Regression-Based Approaches[J].IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing,2012,5(2):354-379.

[5] Dobigeon N,Tourneret J Y,Richard C,et al.Nonlinear Unmixing of Hyperspectral Images:Models and Algorithms[J].IEEE Signal Processing Magazine,2013,31(1):82-94.

[6] 贾森.非监督的高光谱图像解混技术研究[D].杭州:浙江大学,2007.

[7] Eches O,Guillaume M.A Bilinear-Bilinear Nonnegative Matrix Factorization Method for Hyperspectral Unmixing[J].IEEE Geoscience & Remote Sensing Letters,2013,11(4):778-782.

[8] 张舒.GPU高性能运算之CUDA[M].中国水利水电出版社,2009:13-21.

[9] 赵颖辉,蒋从锋.遥感影像的高性能并行处理技术研究[J].计算机技术与发展,2014(7):201-205.

[10] 罗耀华,郭科,赵仕波.基于GPU的高光谱遥感MNF并行方法研究[J].四川师范大学学报(自然科学版),2013,36(3):476-479.

[11] 罗耀华,郭科,赵仕波.基于线性光谱模型的混合像元分解高性能计算研究[J].物探化探计算技术,2013(3):344-348.

[12] 叶舜.基于GPU的高光谱图像混合像元分解并行优化研究[D].南京理工大学,2014.

[13] Bertsekas D P.Constrained optimization and Lagrange multiplier methods[M].New York:Academic,1982.

[14] 王丽姣.基于单形体体积增长的高光谱图像端元提取及快速实现[D].浙江大学,2015.

[15] Heinz D C,Chein-I-Chang.Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery[J].IEEE Transactions on Geoscience & Remote Sensing,2002,39(3):529-545.

SPECTRALUNMIXINGPARALLELCOMPUTINGOFNONNEGATIVEMATRIXDECOMPOSITIONBASEDONFANMODEL

Jiang Zite Zhao Liaoying Zou Jialin

(SchoolofComputerScienceandTechnology,HangzhouDianziUniversity,Hangzhou310018,Zhejiang,China)

The generalized non-negative matrix factorization algorithm based on Fan model is an effective nonlinear hyperspectral unmixing algorithm without the pure pixel assumption. First, the parallel optimization algorithm based on CUDA programming model and memory model was designed for the fast implementation of the generalized nonnegative matrix factorization algorithm based on FAN model. Then, task assignment and thread mapping were performed for the serial and parallel parts of the optimized algorithm and reasonable kernel functions were designed for the implementation of the key steps. The spectral unmixing experiment on real hyperspectral data shows that the CUDA parallel optimization algorithm can achieve higher speedup than the serial algorithm, which verifies the validity of the proposed algorithm.

Generalized non-negative matrix factorization Nonlinear mixture model Parallel computing Hyperspectral image

2017-01-17。国家自然科学基金项目(61571170)；浙江省自然科学基金项目(LZ14F030004)。江子特，本科生，主研领域：计算机应用与软件。赵辽英，教授。邹佳林，硕士生。

TP751.1

A

10.3969/j.issn.1000-386x.2017.12.018