一种基于线性化模型的并网逆变型分布式电源故障特性分析方法

沈渭程，张惠智，马富齐，赵耀，董开松，马喜平

（1.甘肃省电力科学研究院，甘肃兰州 730050；2.西安理工大学，陕西西安 710048）

一种基于线性化模型的并网逆变型分布式电源故障特性分析方法

沈渭程1，张惠智2，马富齐2，赵耀1，董开松1，马喜平1

（1.甘肃省电力科学研究院，甘肃兰州 730050；2.西安理工大学，陕西西安 710048）

随着能源危机的进一步加剧和可再生能源发电技术的快速发展，逆变型分布式电源（IIDG）接入电网成为必然发展趋势。逆变型分布式电源的接入一方面增加了电力系统运行的灵活性、环保性，另一方面也给系统的电压调节、保护协调等带来了新问题[1]。其中，逆变型分布式电源接入后的故障特性关系到电力系统暂态运行的稳定性和可靠性，是最值得关注的问题之一[2]。然而受逆变型分布式电源本身控制方式[3]的影响，其故障特性具有与传统电源完全不同的特征，传统的故障分析方法不再适用于含逆变型分布式电源的系统，这给逆变型分布式电源的故障特性分析带来了很大的困难。

针对这一问题，国内外学者进行了大量研究，研究方法大致可以分为两种。一种方法是将逆变型分布式电源等效为恒功率源，使用潮流计算方法研究逆变型分布式电源的故障特性。如文献[4]以逆变型分布式电源输出正序功率恒定为前提，建立了逆变型分布式电源的恒功率源模型，结合潮流计算和短路计算，得到分布式电源在短路发生时的短路电流值。文献[5]将逆变电源等效为正序恒功率源或者限流模式下的恒流源，进行逆变型分布式电源故障分析。另外一种方法是按照逆变型分布式电源的控制方程，将其等效为正序压控电流源，使用传统的对称分量法进行故障分析。文献[6]通过分析低压穿越控制下的逆变型分布式电源特性，建立了逆变型分布式电源的正序压控电流源模型，适用于对称故障暂态分析。文献[7]提出了在一种限流控制下的逆变电源电流特性，将逆变电源等效为正序电流源与电容的并联模型，进行暂态分析。文献[8]在文献[7]的基础上针对正序分量控制的逆变型分布式电源提出了压控电流源的等值模型，通过建立逆变型分布式电源输出电流与接入点正负序电压之间的关系，构造含分布式电源的配网相间短路故障分析精确模型。

以上两种方法均在一定条件下反映了逆变型分布式电源的故障特性，但是仍存在一些问题。方法一所采用的逆变型分布式电源恒功率源模型建立的前提是逆变型分布式电源输出功率恒定不变，但是对特定的控制方法，在发生不对称故障时，受不对称分量影响，逆变电源的输出功率将产生波动[9]，而模型中仍以输出功率恒定为前提进行计算，必然会导致一定量的误差。方法二使用对称分量法进行故障分析，要求逆变型分布式电源模型具有线性特性，正序压控电流源模型中逆变型分布式电源只输出正序电流，且正序电流只与正序电压相关，满足线性条件。但是在发生非对称故障时，一些逆变型分布式电源会输出负序电流[9]，且正负序电流与正负序电压之间有非线性的耦合关系，则正序压控电流源模型不再适用。

本文在分析现有并网逆变型分布式电源控制策略的基础上，针对逆变型分布式电源非线性的特性，提出了一种线性化的方法，建立了逆变型分布式电源的故障模型，避免了逆变型分布式电源输出功率波动对故障分析的影响，同时使得传统的故障分析方法能够适用于含逆变型分布式电源的系统；利用该方法对含逆变型分布式电源的系统进行了故障特性分析，并将理论分析与实验结果进行了对比验证。

1 并网逆变型分布式电源控制策略及其特性

1.1 并网逆变型分布式电源系统

图1所示为简单的并网逆变型分布式电源系统，包括直流电源、逆变器、滤波器、出口变压器、阻抗、接入系统以及控制回路。其中控制回路采用常见的外环功率内环电流的双闭环控制，功率外环产生电流内环的参考值，由电流内环输出调制信号。

为分析方便，对图1所示系统作如下说明：

图1 并网逆变型分布式电源系统Fig.1 Grid-connected IIDG system

1）逆变型分布式电源故障发生前后有功功率的参考值不发生变化。直流电源受最大能量输出控制，输出能量具有一定惯性，故障发生后有功功率的参考值不发生变化。

2）逆变型分布式电源在故障期间不输出无功。受并网逆变型分布式电源功率因数的限制[10]，通常逆变型分布式电源在正常运行时输出的无功功率接近于0。在故障发生时受逆变器容量限制，大部分的小型分布式电源并无输出无功功率补偿电压的能力[9]。

3）逆变器采用三相三线接线方式，不存在零序分量。

4）逆变型分布式电源输出电流严格跟踪参考电流。

图1所示系统发生故障时，有功功率的参考值为Pref，无功功率的参考值为0，逆变型分布式电源出口处瞬时电压矢量v=v++v-，瞬时电流矢量i=i++i-，v+、v-、i+、i-分别为正负序电压、电流矢量。

1.2 逆变型分布式电源并网控制策略

逆变型分布式电源并网控制策略多种多样，以功率参考值Pref、Qref不变为前提，可使用不同的控制方法实现有功功率波动最小化、无功功率波动最小化、输出电流不对称度最小化、输出电流谐波最小化等目标。现有逆变型分布式电源并网控制策略原理[9]见表1。功率外环参考值Pref恒定，Qref恒等于零。电流内环的参考值ipref随控制目标的变化而改变。控制策略1-5分别实现瞬时有功功率恒定、平均有功功率恒定、负序电流为零、正序电流无谐波、正序负电流无谐波的控制目标。

表1中pref为有功功率参考值，ipref为有功电流参考矢量分别为正负序电流参考矢量，且满足

表1 逆变型分布式电源控制策略原理Tab.1 Control strategies of IIDG

式中：Imax为电流环的限流值。

1.3 逆变型分布式电源控制策略的故障特性

为建立逆变型分布式电源的故障等效模型，从故障条件下功率输出特性和正负序电流特性两个方面对上述5种控制策略进行分析。

1.3.1 功率输出特性

瞬时功率[11]的定义为

当不对称故障发生时，由于负序量的存在，瞬时功率中含有v+i-pref和v-i+pref带来的二次谐波分量[12]，瞬时有功功率和瞬时无功功率均会产生不同程度的波动。定义瞬时功率波动：

可得不同控制策略下故障时的瞬时功率波动，见表2。

表2 不同控制策略下的故障瞬时功率波动Tab.2 Power fluctuations under different control strategies

由表2可见，在不同控制策略下，对称故障时逆变电源输出功率保持不变，非对称故障时受负序电压的影响，会存在不同程度的波动（策略1除外），因此在非对称故障发生时，不能单纯地将逆变电源等效为恒功率源进行故障特性分析。

1.3.2 正负序电流特性

表1所示的五种控制策略下逆变型分布式电源输出的正负序电流如表3所示。

表3 不同控制策略下的正负序电流分量Tab.3 Sequence current under different control strategies

不同控制策略下的正负序电流用通式表达如下：

对于不同的控制策略，α可取值为－1、0、1，β可取值为0、1。上式中α、β均取0时即为控制策略4所对应的正序压控电流源模型。

发生不对称故障出现负序电压时，正序压控电流源模型仅适合分析控制策略4控制下的逆变型分布式电源故障特性。其他控制策略下的逆变型分布式电源输出的电流并不满足正序压控电流源的模型，且正负序电流与电压之间均有非线性的耦合关系，不满足对称分量法所要求的线性条件，因此不能使用对称分量法对式（4）所示的正负序电流源模型进行故障分析。

综上，在现有的并网逆变型分布式电源的控制策略下，采用恒功率源模型或正序压控电流源模型均具有一定局限性，需要寻求新的方法进行逆变型分布式电源故障分析。

2 并网逆变型分布式电源暂态特性分析方法

2.1 并网逆变型分布式电源线性化模型

对称分量法是传统的故障分析方法，适用于对称特别是不对称故障分析。其使用的前提条件是所分析的对象具有线性特性，使正负零序分量满足叠加定理。因此，要建立的逆变型分布式电源模型必须具有线性特性，才能使用对称分量法进行故障分析。而现有控制策略下（除控制策略4之外），逆变型分布式电源均具有非线性特性，为使用对称分量法进行逆变型分布式电源故障分析，本文提出了一种将逆变型分布式电源非线性特性线性化的方法。

发生故障时，逆变型分布式电源输出电流严格跟踪参考电流。输出电流未达到限流值时，将矢量模值展开为矢量及共轭矢量的乘积，根据式（4）可得

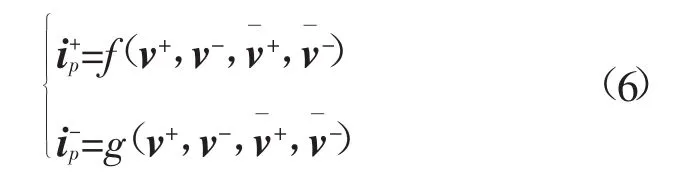
式中，逆变器出口正负序电压v+、v-及其共轭和正负序电流均为未知量。为建立电流与电压之间的线性关系，将在任意取定的非零初值处一阶泰勒展开，得：

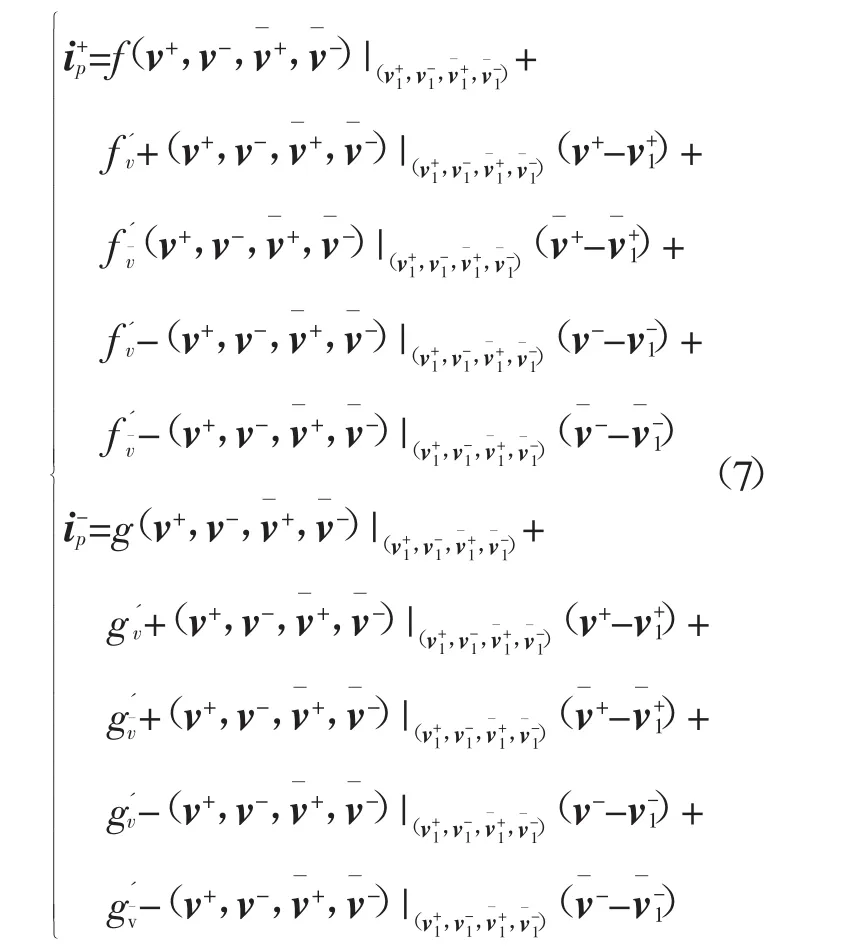
由上式构造分别与正负序电压v+和v-线性相关的电流量

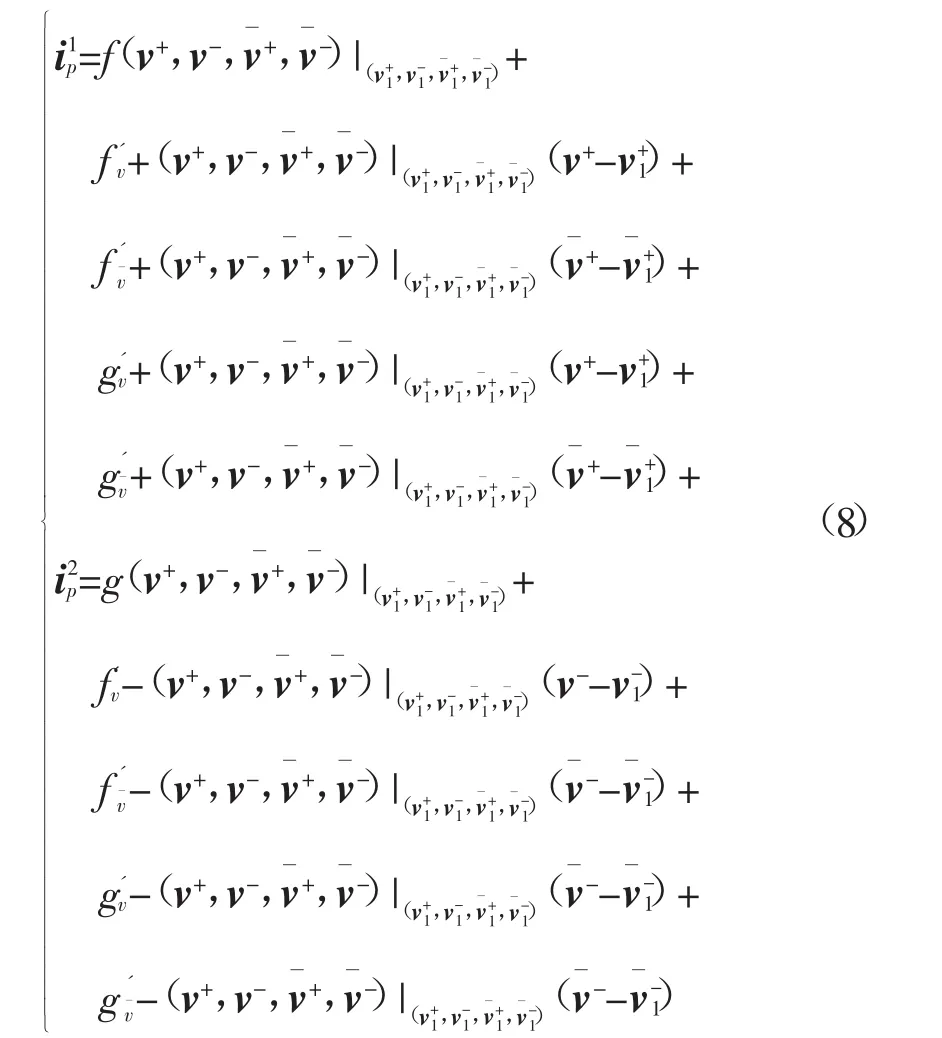
由式（8）可以看出，构造得到的电流之和仍等于正负序电流之和：

图2 逆变型分布式电源的线性压控电流源模型Fig.2 Linear voltage-controlled current source model of IIDG

逆变型分布式电源输出电流达到限流值时，为优先保证正序有功电流输出，同时降低输出电流的不对称度，输出电流方程为

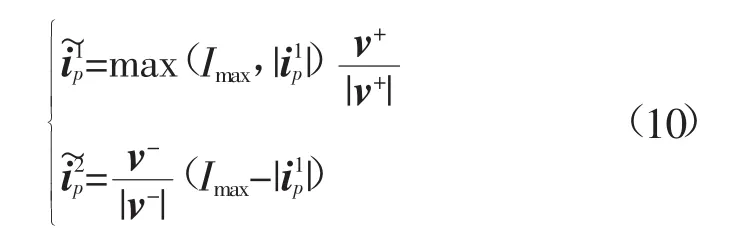
根据上式，可将输出电流达到限流值的逆变型分布式电源等效为如图2（b）所示的受控电流源模型。

图2所示模型不同于恒功率源模型，不受各种控制策略下功率波动影响，同时避免了正序压控电流源模型在负序电流存在时的不适用性。该模型满足电流电压之间的线性关系，且正负序网络之间不存在耦合，可用于分析表1中各种控制策略下发生对称及不对称故障的逆变型分布式电源故障特性。

2.2 并网逆变型分布式电源暂态分析

根据图2（a）所示的逆变型分布式电源压控电流源模型，可以建立图1所示系统的正负序网络图如图3。

图3 正负序分量网络图Fig.3 Positive and negative sequence network

根据不同类型故障的边界条件，将方程（8）与根据复合序网列写的回路电压方程联立解得新的电压（v+，v-），令：

取n=2，代入迭代方程（12）：

停止迭代，得到精确的正负序电压v+、v-，代入式（4）得到正负序电流

图2（b）所示的输出电流达到限流值的模型也可用类似的方法分析。

3 相间短路暂态特性分析

本文以在控制策略1（见表1）控制下的逆变型分布式电源系统发生相间短路为例进行详细说明。

逆变型分布式电源输出电流未达到限流值时，输出的正负序电流方程为：

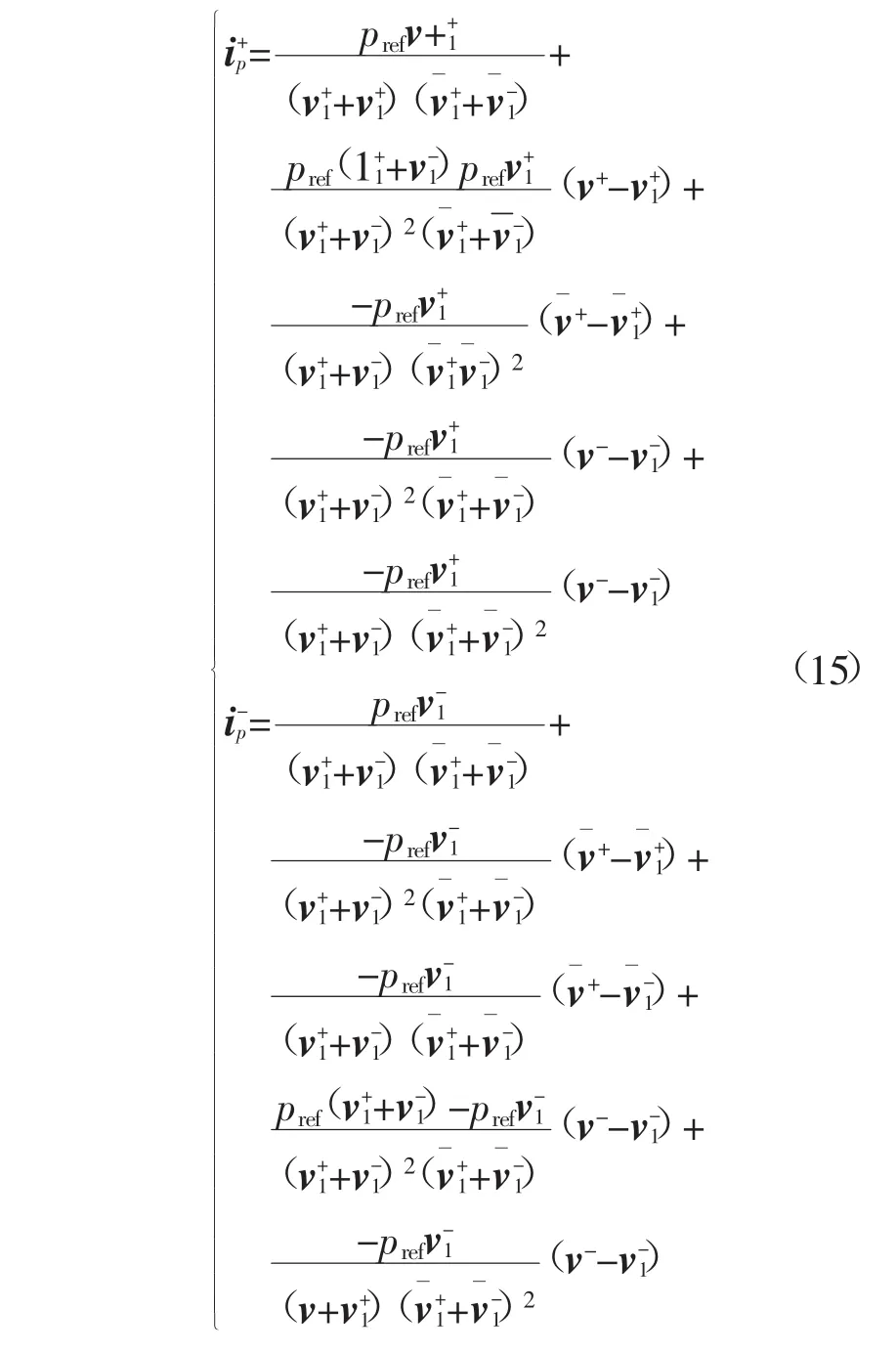
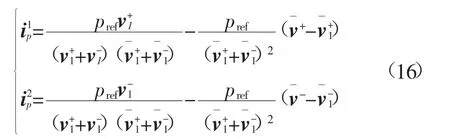
参考图1所示系统，发生相间短路时的复合序网图如图4所示。

图4 相间短路复合序网图Fig.4 Complex sequence network for phase-to-phase fault

图4中：v+、v-为逆变器出口处的正负序电压；为逆变器输出的等效电流；Zline为逆变器出口到故障发生处的等效阻抗（包含变压器阻抗）；Zg为故障发生处到系统的等效阻抗；Zf为单相短路阻抗；us为系统电压矢量。

根据图4列写回路电压方程

与式（16）联立，按照第2节所述迭代计算方法即可得到故障发生后的正负序电压v+、v-，代入式（14）可得电流

输出电流达到极限时，输出电流方程为

同理，可列写电压回路方程

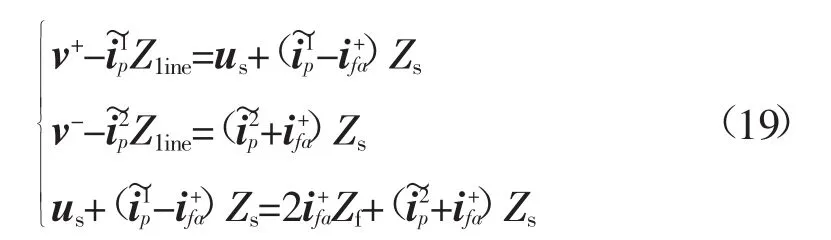
与式（18）联立，按照第2节所述迭代计算方法得到故障发生后的正负序电压v+、v-，代入式（4）得电流

4 实验验证

本文以Aurora公司提供的power-one系列的光伏逆变器为研究对象，搭建了图1所示的实验平台，进行了未达到限流和限流模式下包括对称和不对称短路在内的故障实验。实验系统中：有功功率参考值Pref如表4（直流电源采用最大功率跟踪控制造成有功功率参考值波动），逆变器侧线路阻抗Z1ine为（0.15+0.1j）Ω，系统侧线路阻抗为（0.5+0.4j）Ω，未限流模式下单相接地阻抗Zf为4.85 Ω，限流模式下接地阻抗Zf为0 Ω，系统侧电压为226∠0°。实验系统中采用控制策略1（参见表1），为对比方便，理论分析只给出该策略下的结果。

表4 实验有功功率参考值Tab.4 Reference of active power during experiments

取正负序电压矢量的初值为（200∠0°，1∠0°），以系统电压us的相位为参考相位，将未达到限流和限流模式下的三相短路及两相短路的故障特性理论分析值和实验结果进行对比如表5、6。

表5 未达到限流模式下故障特性理论分析与实验结果对比（序量）Tab.5 Comparison of analysis and experiment results of fault characteristic without current limit（sequence）

表6 达到限流模式下故障特性理论分析与实验结果对比（序量）Tab.6 Comparison of analysis and experiment results of fault characteristic with current limit（sequence）

由表5可见，在未到达限流时，三相短路故障时逆变型分布式电源输出正序电压和正序电流，两相短路时输出正、负序电压和电流。显然，三相短路和两相短路故障特性的理论分析结果和实验结果基本吻合，负序量的出现并未影响算法的精度，证明理论分析方法能很好地用于对称及不对称故障特性的分析。

当逆变型分布式电源输出的短路电流达到限流值时，正序电流被限定在16 A，负序电流被限定在0 A，如表6所示，三相短路时逆变型分布式电源只输出正序电压和电流，两相短路时输出正负序电压和正序电流，理论分析结果同样与实验结果相一致，证明该分析方法同样适用于限流模式下的分布式电源故障特性分析。

为进一步研究逆变型分布式电源在对称及不对称故障下的特性，本文将逆变型分布式电源故障条件下输出的正负序电压、电流转换为相电压、相电流，与正常运行时的电压、电流进行对比，见表7、8。

由表7可见，逆变型分布式电源输出的故障电流未达到限流值时，三相短路条件下输出的三相电压同时减小，三相电流同时增大，故障发生时输出的电压电流仍然保持三相对称。两相短路条件下故障相电压减小，受短路阻抗影响，故障相电压并不相等，故障相电流增大，非故障相电流基本不变。

由表8可见，逆变型分布式电源输出的故障电流达到限流值时，三相短路条件下，三相电压同时减小，三相电流同时增大，受限流作用，电流维持在限定值16 A，三相电压电流均保持对称。两相短路条件下，由于正序电流为限定值、负序电流为零，故障相电压减小，非故障相电压保持不变，故障相和非故障相电流均为限定值，三相电压出现不对称，而三相电流在限流作用下保持对称，这一点与传统的故障特性有很大区别。

表7 未达到限流模式下故障特性理论分析与实验结果对比（相量）Tab.7 Comparison of analysis and experiment results of fault characteristic without current limit（phasor）

表8 达到限流模式下故障特性理论分析与实验结果对比（相量）Tab.8 Comparison of analysis and experiment results of fault characteristic with current limit（phasor）

5 结论

针对在不同并网逆变型分布式电源控制策略下，逆变型分布式电源的功率波动性和非线性特性，本文提出了一种基于线性化模型的故障分析方法。利用所提出的方法对含逆变型分布式电源系统在限流和非限流模式下的对称及不对称故障特性进行了分析，得到了不同条件系的对称和不对称故障的电气量变化特征，从序量特征和相量特征两方面将分析结果与实验结果进行了对比，验证了本文所提出的方法的正确性。

本文所提出的方法适用于各类具有功率波动特性和非线性特性的逆变型分布式电源，解决了恒功率源模型和正序压控电流源模型在特定控制策略下不适用的问题。

本文针对逆变型分布式电源无无功补偿的情况进行了分析，实际上对于具有无功补偿能力的逆变型分布式电源，也可以将其输出的无功电流线性化以后按照类似的方法进行分析。

[1]王成山，李鹏.分布式发电、微网与智能配电网的发展与挑战[J].电力系统自动化，2010，34（2）：10-14.WANG Chengshan，LI Peng.Development and challenges of distributed generation，the micro-grid and smart distribution system[J].Automation of Electric Power Systerms.2010，34（2）：10-14.

[2] BARAN M E，El-MARKABY I.Fault analysis on distribution feeders with distributed generators[J].IEEE Transactions on Power System，2005，2（4）：945-950.

[3]王成山，李琰，彭克.分布式电源并网逆变器典型控制方法综述[J].电力系统及其自动化学报，2012，24（2）：12-20.WANG Chengshan，LI Yan，PENG Ke.Overview of typical control methods for grid-connected inverters of distributed generation[J].Poceedings of the CSU-EPSA，2012，24（2）：12-20.

[4]王成山，孙晓倩.含分布式电源配电网短路计算的改进方法[J].电力系统自动化，2012，36（23）：54-58.WANG Chengshan，SUN Xiaoqian.An improved short circuit calculation method for distribution network with distributed generations[J].Automation of Electric Power Systems，2012，36（23）：54-58.

[5]J.MORREN，S.W.H.DE HAAN，J.A.FERREIRA.Model reduction andcontrol of electronic interfaces of voltage dip proof dg units[C]//PowerEngineering Society General Meeting，2004，2：2168-2173.

[6]吴争荣，王钢，李海锋，等.计及逆变型分布式电源控制特性的配电网故障分析方法[J].电力系统自动化，2012，36（18）：92-96.WU Zhengrong，WANG Gang，LI Haifeng，et al.Fault characteristics analysis of distribution networks considering control scheme of inverter interfaced distributed generation[J].Automation of Electric Power Systems， 2012， 36（18）：92-96.

[7]CORNELIS A.PLET，M.GRAOVAC，TIMOTHY C.Green.faultresponse ofgrid-connected inverter dominated networks[C]//Power and Energy Society General Meeting，2010，MN，USA.

[8]吴争荣，王钢，李海锋，等.含分布式电源配电网的相间短路故障分析[J].中国电机工程学报，2013，33（1）：130-136.WU Zhengrong，WANG Gang，LI Haifeng，et al.Analysis on the distribution network with distributed generators under phase-to-phase short-circuit faults[J].Proceedings of the CSEE，2013，33（1）：130-136.

[9] PEDRO RODRIGUEZ，ADRIAN V.TIMBUS.Flexible active power control of distributed power generation systems during grid faults[J].IEEE Transactions on Industrial Electronics，2007，54（5）：2583-2592.

[10]IEEE Standard for interconnecting distributed resources with electric power systems[S].IEEE15471，2008.

[11]HESAM YAZDANPANAHI，YUN WEI LI.A new control strategy to mitigate the impact ofInverter-based DGs on protection system[J].IEEE Transactions on Smart Grid，2012，3（3）：1427-1435.

Analysis on the Grid-Connected Inverter-Interfaced Distributed Generator Faults Based on a Linearization Model

SHEN Weicheng1，ZHANG Huizhi2，MA Fuqi2，ZHAO Yao1，DONG Kaisong1，MA Xiping1
（1.Gansu Electric Power Research Institute，Lanzhou 730050，Gansu，China；2.Institute of Water Resources and Hydro-Electric Engineering，Xi’an University of Technology，Xi’an 710048，Shaanxi，China）

Due to power fluctuations and non-linearization of the inverter-interfaced distributed generator（IIDG），the existing fault analysis method has some limitations.Based on a study of various control strategies，this paper proposes a novel linear voltage controlled current model applicable in multiple control strategies of the IIDG，and the proposed model can avoid the effect of power fluctuations and facilitate linearization of the output current and voltage of the IIDG.Furthermore，the traditional symmetrical component and iteration method is used to analyze the fault characteristic of the IIDG.The theoretical results have been validated by experiment results.

inverter-interfaced distributed generator;fault response;linearization;symmetrical component method

受逆变型分布式电源功率波动和控制特性的非线性影响，现有的逆变型分布式电源故障特性分析方法存在一定的局限性。在研究现有并网逆变型分布式电源控制策略的基础上，提出了一种适用于多种控制策略的逆变型分布式电源线性压控电流源模型，避免了功率波动对故障分析的影响，同时实现了控制量电压和受控量电流之间的线性化。在此基础上，利用传统故障分析所用的对称分量法和迭代法分析逆变型分布式电源系统的故障特性，并在实际系统中进行了实验验证。

逆变型分布式电源，故障特性，线性化，对称分量法

1674-3814（2017）09-0131-08

TM773

A

国家电网科技项目（522722150012）。

Project Supported by the Science and Technology Program of the State Grid Corporation of China（522722150012）.

2016-11-16。

沈渭程（1987—），男，工程师，主要从事发电企业运营管理工作；

张惠智（1988—），女，博士，讲师，主要研究方向为电力系统自动化；

马富齐（1994—），男，硕士研究生，研究方向为电力系统新能源；

赵 耀（1986—），男，工程师，主要从事电网的运行与故障检测；

董开松（1966—），男，硕士，高级工程师，国网工程技术专家，主要研究方向为新能源发电及并网技术；

马喜平（1987—），男，工程师，研究方向为电网安全稳定运行。

（编辑 李沈）