考虑分布式发电供电概率的配电网重构

殷豪，李德强，孟安波，苏泓霖，黄海涛，洪俊杰

（广东工业大学自动化学院，广东广州 510006）

考虑分布式发电供电概率的配电网重构

殷豪，李德强，孟安波，苏泓霖，黄海涛，洪俊杰

（广东工业大学自动化学院，广东广州 510006）

随着分布式电源（DG）在电力系统中研究的深入，配电网接入DG成为了热门。DG包括可再生和非可再生2部分，可再生DG具有持续利用周期长和污染小的优点，但其供电能量会跟随天气等因素变化，给供电网络带来波动性。非再生DG具有稳定性强和效率高等优点，但是在供电过程中有污染大和持续利用周期短等缺点。从能源持续利用周期角度考虑，可再生DG接入配电网的研究是非常必要的。

传统配电网具有闭环设计、开环运行等特点，正常运行时网络呈现辐射状态，是一个单电源供电系统，通过联络开关和分段开关对配电网进行重构以达到降低网损[1]、均衡负荷[2]、提高电压质量[3]等特性。当配电网接入DG以后会成为一个遍布电源的供电系统，提升了整体网络的可靠性[4-5]但，也降低了网络的稳定性。配电网重构算法大致可分为数学方法[5-6]、启发式方法[7-10]和人工智能算法[11-14]等。文献[15]在配电网重构过程中考虑了可靠性因素和网损，重新构建目标函数，使函数适应于含有DG的配电网系统，仿真部分是标准的IEEE33节点和PG&E 69节点网络，结果证明了配电网接入DG可以提升最低节点电压和减少网损。文献[11]目标函数在网损最小的情况下规定了节点电压的偏差，使得节点电压在重构中进行优化。算法采用的是（particle swarmoptimizatio，PSO）算法，PSO算法在解决多变量非线性的优化问题中具有一定的优势。文献[16]在配电网重构过程中考虑了风电出力的随机性，通过切入风速、额定风速和切除风速将风电出力划分为3种不同的出力状态。根据风速近似服从威尔布分布，计算3种出力状态的概率。

本文在配电网重构过程中加入2种类型的DG，分别是风力和光伏DG，根据风速和光照强度建立不同的概率密度函数，同时考虑不同状态下DG的供电概率进行配电网重构。算法采用纵横交叉算法（CSO），CSO算法由双搜索机制组成，分别是横向交叉机制和纵向交叉机制，2种机制与竞争算子的完美结合，有效解决了重构优化中的问题。

1 DG供电概率模型

1.1 风电功率的概率模型

风能在通过风力发电机转化为电能的过程中，风电功率Pwind与风速v具有一定的函数关系：

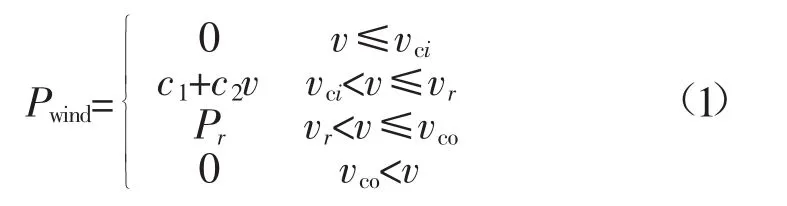
式中：Pr为风力发电的额定输出功率；vci、vr、vco分别为测得的切入风速、额定风速和切除风速；系数c1和c2的表达式为：c1=Prvci/（vci-vr），c2=Pr/（vr-vci）。

风速有4种区间分布，从而产生4种不同的风电输出功率。根据风速与输出功率之间的关系建立3种不同的状态[8]，分别是状态Sw1（v≤vci和vco＜v）、状态Sw2（vci＜v≤vr）、状态Sw3（vr＜v≤vco）。风速近似服从双参数的威布尔分布：

式中：c为尺度参数；k为形状参数。这些参数可以通过实测数据拟合得到。根据风速的概率密度函数，考虑3种不同状态的配电网重构，每种状态都有一定的发生概率：

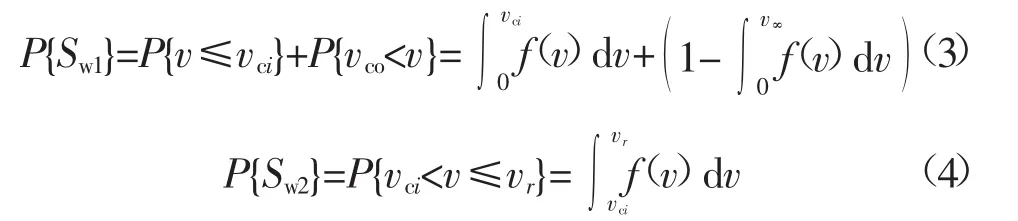
式中：P{Sw1}、P{Sw2}和P{Sw3}分别为状态Sw1、状态Sw2和状态Sw3发生的概率。

1.2 光伏发电功率的概率模型

光伏发电功率与光照强度具有一定的函数关系，光照强度服从Beta分布，其概率密度函数为：

式中：α和β是形状参数，可以通过实测数据拟合得到；rmax和r分别为最大光照强度和实际光照强度；Γ为Gamma函数。

当达到一定光照强度时，会输出相对稳定的功率。根据某地区光照强度与输出功率之间的关系，建立2种不同的状态，分别是Sr1（r≤rmin）、Sr2（rmin＜r≤rmax）。根据光照强度概率密度函数，考虑2种不同光照强度状态情况下的配电网重构，每种状态发生的概率为：

式中：P{Sr1}、P{Sr2}分别为状态Sr1、状态Sr2发生的概率。

1.3 基于供电概率下的网络重构模型

本文以网损最小作为目标函数，同时考虑DG供电概率对配电网络的影响，对风力发电和光伏发电的状态进行组合，得出6种混合状态分别是{Sw1&Sr1}、{Sw1&Sr2}、{Sw2&Sr1}、{Sw2&Sr2}、{Sw3&Sr1}和{Sw3&Sr2}。因2种状态相互独立，得出P{Swi&Srj}=P{Swi}P{Srj}，根据混合状态对网络进行重构，目标函数为：

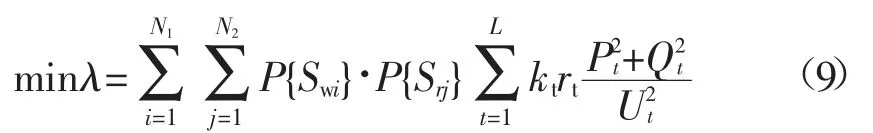
式中：N1为风力发电的状态总数；N2为光伏发电的状态总数；L为系统支路总数；kt为支路通断情况（0表示打开1，表示闭合）；rt为支路电阻；Pt和Qt为有功功率和无功功率；Ut为支路注入节点电压幅值。

1）不等式约束：

式中：Ukmin和Ukmax为节点k的电压上限和下限；Ik，k+1，max为流过k到k+1段的电流最大值；Sk和Skmax为线路流过的功率和最大容许值。

2）网络约束。网络重构后不出现“回路”和“孤岛”。

2 网络编码方式

配电网的编码方式决定程序运行效率，通常所用编码方法有二进制编码、支路编码等，其中二进制编码方式通过0和1来表示网络中开关的通断，这种编码会因为网络规模而出现“组合爆炸”等情况，不利于实际电网的应用。支路编码对网络支路中打开的开关进行编码，一组支路中打开的开关与编码的数字相对应，同时支路编码方法设定某一规则使得打开方式不会产生“孤岛”和“回路”，这种编码方式避免了二进制编码方式产生“组合爆炸”的问题。但是编码方式因为网络支路关联度高而较难设定规则。本文采用环路编码方式化简步骤（见图1）。

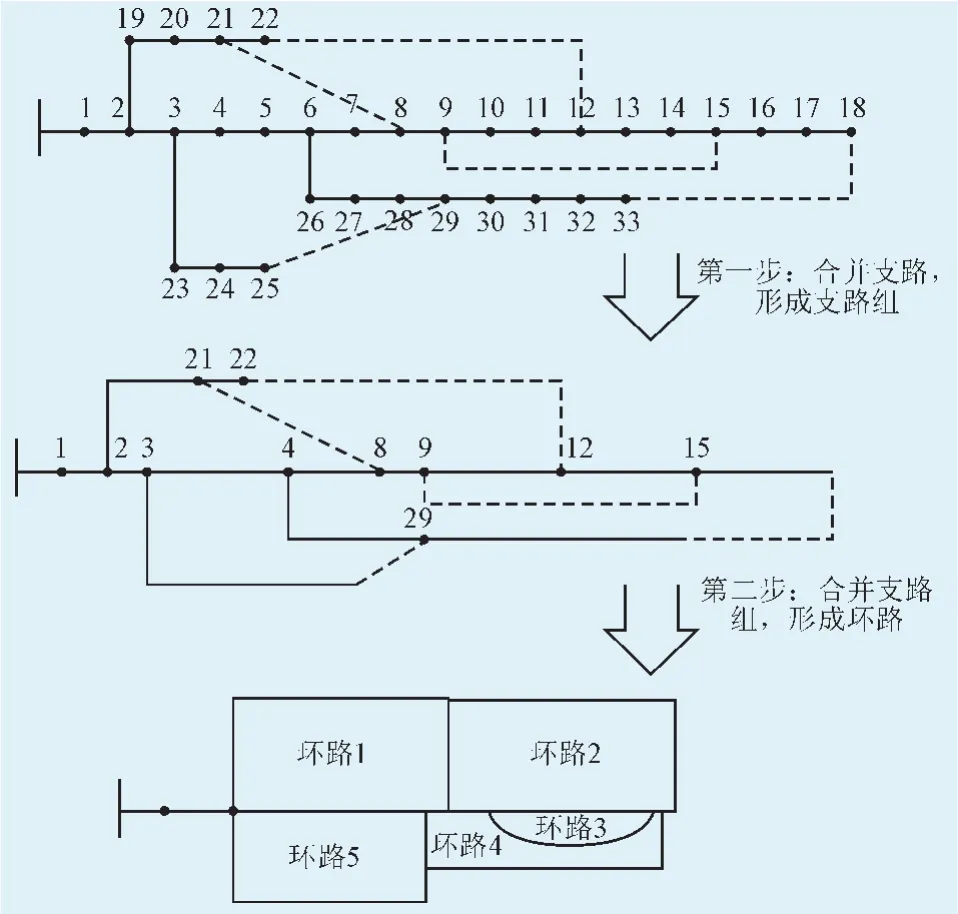
图1 网络化简图Fig.1 Process of the simplifying of distribution network

这种编码方式可以避开二进制编码方式“组合爆炸”的情况，同时仅有2条规则需要设定：

1）断开开关数等于环路总数。

2）相邻环路不在相交支路同时断开。

图1中共包含5个回路，编码有5个维度。每个环路编码的上限由环路中拥有支路总数决定，下限要大于1（每个回路必须要打开一个开关）。例如一个粒子的编码是[1 2 5 8 9]，代表第一环路的第一个开关、第二个环路的第二个开关、第三个环路的第五个开关、第四个环路的第八个开关和第五个环路的第九个开关打开，同时打开开关的组合要满足2条规则，这样就完成了一次编码。

3 CSO算法

纵横交叉算法（CSO）由横向交叉算子、纵向交叉算子和竞争算子3部分组成[17]。其搜索过程是2种交叉算子更新父代种群，从而得到子代种群，通过竞争算子将2代种群中适应度高的粒子保留下来参与下一次迭代。其中的纵向交叉算子可以使陷入局部最优的粒子跳出，加快收敛全局最优解。

3.1 横向交叉算子

横向交叉算子运算过程是将2个不同粒子进行交叉运算，交叉前和交叉后的粒子分别是父代粒子和子代粒子，每个粒子代表配电网重构的一种开关组合。假设同一代的2个粒子分别为X（i，d）和X（j，d），则它们的子代为：

式中：MShc（i，d）和MShc（j，d）为经过交叉运算后的子代粒子；D为解的维度；M为解的规模；r1、r2为介于[0，1]之间的随机数；c1、c2为介于[-1，1]之间的随机数。

3.2 纵向交叉算子

纵向交叉算子运算过程将同一个粒子不同维度进行交叉运算，交叉前和交叉后的粒子分别是父代粒子和子代粒子。假设父代粒子X（i）的第d1维和第d2维进行交叉，则它们的子代为：

式中：r为介于[0，1]之间的随机数；MSvc（i，d1）为父代X（i，di）为经过交叉运算后产生的子代粒子。

3.3 竞争算子

竞争算子是一种淘汰机制，作用是将2代粒子的适应度进行对比，淘汰掉适应度差的解，保留剩余的粒子参与下一次迭代。竞争算子如图2所示。

竞争算子可以设定淘汰率，使其更加适应于整体种群的进化。

经过交叉运算后的粒子并不是整数，不能正确表示环路编码方式的开关组合，这时引入sigmoid将运算后的粒子离散化，使其符合编码方式：

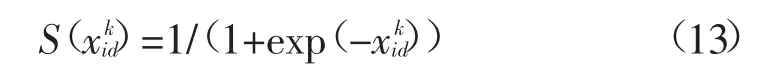
离散化约束条件为：

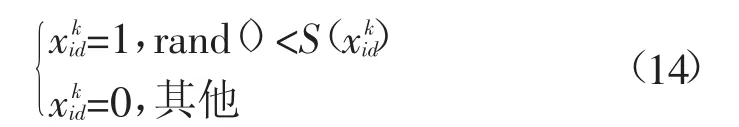
图2 竞争算子的流程Fig.2 Procedure of the competitive operator

3.4 重构流程图

重构首先确定DG的场景，其次根据场景进行划分相应DG输出概率，最后带入带配电网中进行重构，具体流程如图3所示。

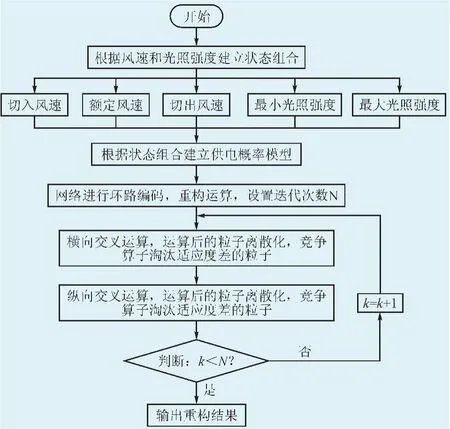
图3 网络重构流程图Fig.3 Flow chart of the network reconfiguration

4 算例分析

4.1 仿真数据

本文以IEEE33节点配电系统和美国PG&E69节点配电系统作为算例。其中IEEE33有37条支路、33个节点和5个联络开关，总负荷为3 715+j2 300 kV·A，额定电压为12.66 kV，网络结构见图1。美国PG&E69节点配电系统有73条支路、69个节点、5个联络开关，总负荷为3 802.19+j2 694.60 kV·A，额定电压12.66 kV，网络结构见图4。潮流计算法方法采用改进的前推回代法[18-19]。

图4 含DG的PG&E69节点系统结构Fig.4 The Structure of PG&E69 nodes system with DGs

同时，2个配电系统接入风力和光伏DG，接入数据见表1和表2。

表1 风力电源数据Tab.1 Data of wind power generations m/s

表2 光伏电源数据Tab.2 Data of photovoltaic power generations

假设风力发电和光伏发电在每种状态下输出稳定的功率，其中风力发电3种状态Sw1、Sw2、Sw3输出的功率分别是0、400 kW、750 kW，概率P{Sw1}、P{Sw2}和P{Sw3}分别是0.442 8、0.395 8、0.161 4（通过式（3）—式（5）计算得到）。光伏发电2种状态Sr1、Sr2输出功率分别是0、300 kW，P{Sr1}和P{Sr2}的概率分别为0.371 9和0.6281（通过式（7）和式（8）计算得到）。根据假设条件将风力发电和光伏发电的状态进行组合，得出6种混合状态。当它们的混合状态是{Sw1&Sr1}时，2个电源的功率输出为0，说明2个DG没有输出功率，这种状态下重构是配电网原始状态下的重构。

本文在重构过程中采用的算法是纵横交叉算法。IEEE33和美国PG&E69节点配电系统均有5个环路，所以解的维度为5。潮流计算方法采用改进前推回代法[10]，使其能适应于含有DG的配电网络潮流计算。设置迭代次数为30次，迭代过程中电压幅值修正量小于10-6kV。

4.2 结果分析

风力发电和光伏发电混合状态下的重构结果如表3和表4所示。

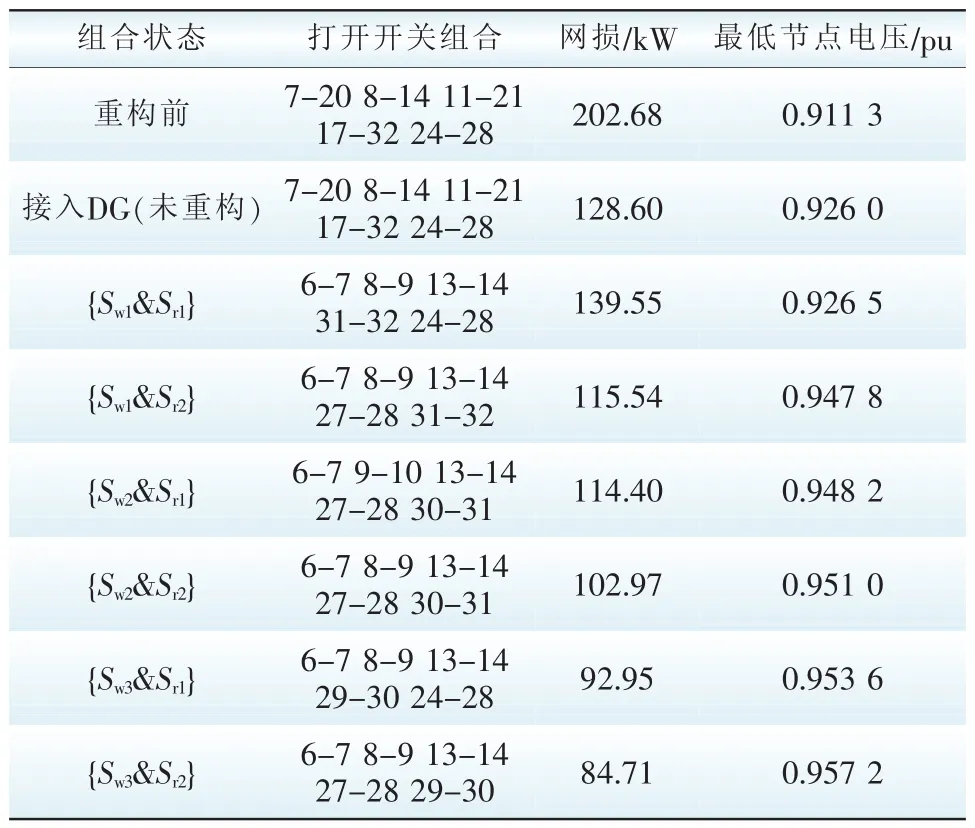
表3 IEEE33节点系统重构结果Tab.3 Result of the reconfiguration on IEEE33

表4 PG&E69节点系统重构结果Tab.4 Result of the reconfiguration on PG&E69

将结果带入式（9）得出值分别是102.31 kW和74.03 kW（IEEE33和PG&E69）。由表3和表4可知，混合状态与原始网络重构结果的网损相比，配电网接入风力和光伏DG后，网损和最低节点电压结果均有改善。同时可以得到配电网接入DG后对进行重构比原始重构所减少的网损进一步增加。当2种DG同时处于最大输出功率时，配电网网损可以减少到原有的61%和63%，IEEE33节点配电系统中DG对网损的影响大于重构的影响，而IEEE69节点重构的影响大于接入DG的影响，说明IEEE33节点和PG&E69节点配电系统接入光风力和光伏DG可以起到降低网损的作用。为不失一般性，将混合状态{Sw2&Sr2}与原始状态中网络的节点电压进行对比，如图5、图6所示。

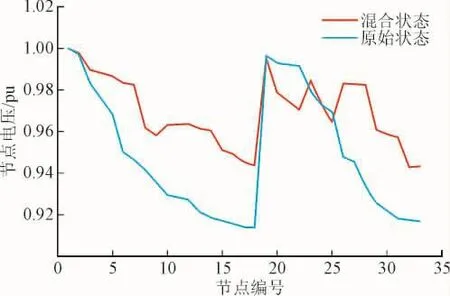
图5 IEEE33节点电压对比Fig.5 Comparison of state voltages in IEEE33 nodes system

图6 PG&E69节点电压对比Fig.6 ComparisonofstatevoltagesonPG&E69nodessystem

由图5、图6可知，在考虑DG供电概率的情况下，IEEE33和PG&E69在接入DG以后大部分节点电压均有提高，说明配电网适当接入DG后可以起到提升电压质量的作用。

为检验算法的优越性，2个配电网络原始状态的迭代曲线，如图7、图8所示。

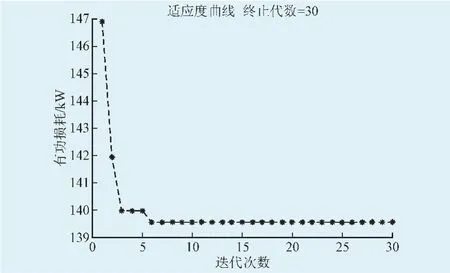
图7 IEEE33节点配电系统收敛曲线Fig.7 Convergence curve of the CSO algorithm on IEEE33 nodes system

图8 PG&E69节点配电系统收敛曲线Fig.8 Convergence curve of the CSO algorithm on PG&E69 nodes system

由图7、图8可知，2个配电系统在重构过程中的第五代左右开始收敛，说明CSO算法搜索能力强，鲁棒性好。

5 结论

本文在考虑风力和光伏DG供电概率的情况下进行配电网重构，同时使用CSO算法进行寻优，得出以下结论：

1）在使用环路编码的条件下，CSO算法具有较强的搜索能力和较好的鲁棒性。

2）当配电网接入风力和光伏DG后，重构后的网损和最低节点电压均有改善。

[1]李振坤，陈星莺，余昆，等.配电网重构的混合粒子群算法[J].中国电机工程学报，2008，28（31）：35-41.LI Zhenkun，CHEN Xingying，YU Kun，et al.Hybrid particle swarm optimization for distribution network reconfiguration[J].Proceedings of the Chinese Society For Electrical Engineering，2008，28（31）：35-41.

[2] 刘柏私，谢开贵，周家启.配电网重构的动态规划算法[J].中国电机工程学报.2005，25（9）：29-34.LIU Bosi，Xie Kaigui，ZHOU Jiaqi.Electrical distribution networks reconfiguration using dymaic programming[J].Programming of the Chinese Society for Electrical Engineering，2005，25（9）：29-34.

[3]毕鹏翔，刘健，张文元.以提高供电电压质量为目标的配网重构[J].电网技术.2002，26（2）：41-43.BI Pengxiang，LIU Jian， ZHANG Wenyuan.Improve voltage quality by reconfiguration of distributed network[J].PowerSystemTechnology，2002，26（2）：41-43.

[4]刘传铨，张焰.计及分布式电源的配电网供电可靠性[J].电力系统自动化，2007，31（22）：46-49.LIU Chuanquan，ZHANG Yan.Distribution network reliability considering distribution generation[J].Automation of Electric Power Systems，2007，31（22）：46-49.

[5] SARMA N D R，RAO K S P.A new 0-1 integer programming method of feeder reconfiguration for loss minimization in distribution systems[J].Electric Power Systems Research，1995，33（2）：125-131.

[6]刘柏私，谢开贵，周家启.配电网重构的动态规划算法[J].中国电机工程学报，2005，25（9）：29-34.LIU Bosi，XIE Kaigui，ZHOU Jiaqi.Electrical distribution networks reconfiguration using dynamic programming[J].Proceedings of the CSEE，2005，25（9）：29-34.

[7] DAS D.A fuzzy multiobjective approach for network reconfiguration of distribution systems[J].IEEE Transactions on Power Delivery，2006，21（1）：202-209.

[8]CIVANLAR S，GRAINGER J J，YIU H，et al.Distribution feeder reconfiguration for loss reduction[J].IEEE Transactions on Power Delivery，1988，3（3）：1217-1223.

[9]毕鹏翔，刘健，张文元.配电网络重构的改进支路交换法[J].中国电机工程学报，2001，21（8）：98-103.BI Pengxiang，LIU Jian，ZHANG Wenyuan.A refined branch-exchange algorithm for distribution networks reconfiguration[J].Proceedings of the CSEE，2001，21（8）：98-103.

[10]LIN Y，ZHIZHONG G.Reconfiguration of electric distribution networks for energy losses reduction[C]//2008 3 rd International Conference on Electric Utility Deregulation and Restructuring and Power Technologies，Nanjuing：IEEE，2008：662-667.

[11]赵晶晶，李新，彭怡，等.基于粒子群优化算法的配电网重构和分布式电源注入功率综合优化算法[J].电网技术，2009（17）：162-166.ZHAO Jingjing，LI xin，PENG Yi，et al.A comprehensive optimization algorithm for injection power of distributed generation and distribution network reconfiguration based on particle swarm optimization[J].Power System Technology，2009（17）：162-166.

[12]靳晓凌，赵建国.基于改进二进制粒子群优化算法的负荷均衡化配电网重构[J].电网技术，2005，29（23）：40-43.JIN Xiaoling，ZHAO Jianguo.Distribution network reconfiguration for load balancing based on improved binary particle swarm optimization[J].Power System Technology，2005，29（23）：40-43.

[13]张凡，张越喜，顾沈卉.基于模拟退火免疫算法的配电网重构[J].南方电网技术，2011，5（5）：42-46.

ZHANG Fan，ZHANG Yuexi，GU Shenhui.Distribution network reconfiguration by simulated annealing immune algorithm[J].Southern Power System Technology，2011，5（5）：42-46.

[14]谢林峰，姚强.基于自适应免疫克隆选择算法的配电网重构[J].南方电网技术，2011，05（6）：81-85.XYE Lienfeng，YAO Qiang.Distribution network reconfiguration based on self-adapting immune clone selection algorithm[J].Southern Power System Technology，2011，5（6）：81-85.

[15]P PAVANI，S N SINGH，Reconfiguration of radial distribution networks with distributed generation for reliability improvement and loss minimization[J].Power and Energy Society General Meeting，2013：1944-9925.

[16]HAO Zhangshuang，MA Gangxu，Network reconfiguration of distribution system with distributed generation using state graph[J].Power and Energy Engineering Conference，2012：2157-4839.

[17]MENG A，CHEN Y，YIN H，et al.Crisscross optimization algorithm and its application[J].Knowledge-Based Systems.2014，67（3）：218-229.

[18]张璐，唐巍，丛鹏伟，等.含光伏发电的配电网有功无功资源综合优化配置[J].中国电机工程学报，2014（31）：5525-5533.ZHANG Lu，TANG Wei，CONG Pengwei，et al.Optimal configuration of active-reactive power sources in distribution network with photovoltaic ceneration[J].Proceedings of the CSEE，2014（31）：5525-5533.

[19]丁明，郭学凤.含多种分布式电源的弱环配电网三相潮流计算[J].中国电机工程学报，2009（13）：35-40.DING Ming，GUO Xuefeng.Three-phase power flow for the weakly meshed distribution network with the distributed generation[J].Proceedings of the CSEE，2009（13）：35-40.

Network Reconfiguration of Distribution System Considering Power Supply Probabilities of Distributed Generations

YIN Hao，LI Deqiang，MENG Anbo，SU Honglin，HONG Junjie
（School of Automation，Guangdong University of Technology，Guangzhou 510006，Guangdong，China）

According to the output of wind and photovoltaic power generations，several power supply states are determined，and the corresponding power supply probability of each state is calculated through the probability density functions of wind speed and illumination intensity respectively.In this paper，the distributed network reconfiguration problem is solved by a novel crisscross optimization algorithm（CSO）which consists of hori zon tal crossover and vertical crossover，in the mixed states which are achieved by combining different states of distributed generations（DGs）.In the CSO，the multiplication of loss and power supply probability is considered as the objective function and the proposed loop encoding strategy is used to avoid“island”and “loops”.In the simulation，IEEE33 and PG&E69 are adopted as the benchmark test systems with the mixed states of wind and photovoltaic power generations considered at the same time.The results show that the network loss can be reduced and the voltage quality can also be improved when the distribution network is integrated with DGs.

distributed generation；distribution network；reconfiguration； power supply probabilities；loop encoding；crisscross optimization algorithm.

根据分布式电源中光伏发电和风力发电的出力情况，划分几种不同供电状态，通过风速和光照强度的概率密度函数，计算它们的供电概率。将2类分布式电源的状态进行组合，得出混合状态，考虑混合状态下的发生概率进行配电网重构，重构目标函数是网损乘以状态发生概率。编码方法采用环路编码方式，通过设定规则避开"孤岛"和"回路"的产生。算法采用纵横交叉算法，它由横向交叉算子、纵向交叉算子和竞争算子组成，搜索过程是2种交叉方式与竞争算子结合的方式进行寻优。仿真部分由IEEE33和美国PG&E69节点配电系统组成，同时考虑光伏发电和风力发电的混合状态及其概率，仿真结果表明配电网系统接入分布式电源以后可以进一步减少网损和提升电压质量。

分布式电源；配电网；重构；供电概率；环路编码；纵横交叉算法

1674-3814（2017）09-0113-06

TM731

A

国家自然科学基金资助项目（51407035）。

Project Supported by the National Natural Science Foundation of China（51407035）.

2017-01-23。

殷 豪（1972—），女，硕士，副教授，研究方向为电力系统稳定与控制；

李德强（1991—），男，通讯作者，硕士研究生，主要研究方向为智能算法在电力系统中的应用；

孟安波（1971—），男，副教授，博士，研究方向为人工智能算法在电力系统中的应用；

苏泓霖（1989—），男，硕士研究生，主要研究方向为智能算法在电力系统中的应用；

黄海涛（1987—），男，硕士研究生，主要研究方向为电力系统中的无功优化；

洪俊杰（1981—），博士，讲师，研究方向为电力电子与电力传动和电机驱动控制。

（编辑 董小兵）