计及需求响应的电动汽车和可再生能源多阶段动态经济环境调度优化模型

侯建朝，侯鹏旺，孙波

（上海电力学院经济与管理学院，上海 200090）

计及需求响应的电动汽车和可再生能源多阶段动态经济环境调度优化模型

侯建朝，侯鹏旺，孙波

（上海电力学院经济与管理学院，上海 200090）

由于化石能源的大量消费，世界各国均面临着严峻的能源和环境问题。为了实现能源和环境的可持续发展，世界各国将风、光等可再生能源作为国家能源发展的战略方向[1-2]。电动汽车与风、光发电协同入网调度，不仅可以提升可再生能源的利用率，而且能够打造一个经济、绿色的电力系统[3-4]。

通过合理地利用需求侧资源，引导电动汽车和用户参与入网调度消纳更多可再生能源发电的问题引起众多学者的关注。文献[5]通过构建电动汽车的智能充电模型，得出电动汽车最优的充电策略，从而提升可再生能源的利用率，但未考虑电动汽车放电的情形。文献[6]建立了同时计及可入网电动汽车、风力发电和光伏发电系统的多目标协同调度模型，采用改进的化学反应算法对电动汽车、风力发电、光伏发电并网调度的多目标优化模型进行求解，结论为：合理地安排电动汽车充放电能够平抑系统负荷波动，增加车主的收益；但风光发电出力有一定误差，没有将其作为变量进行优化。文献[7]运用模糊求解策略将风、光发电与电动汽车多目标优化调度模型转为单目标函数，从而提升风光发电利用率，但没有基于火电机组调度出力进行建模。文献[8]将基于V2G模式下的各时段电动汽车充放电功率和火电机组出力作为变量，建立了包含V2G的电力系统动态经济环境调度（dynamic economic emission dispatch，DEED）模型，对火电机组的发电费用和污染物排放量进行优化，但没有考虑可再生能源入网调度和电力用户的需求响应。文献[9]基于电价响应下多类用户参与电力系统入网调度情景，建立含风电的优化调度模型，得出合理的价格机制能够使发电侧与用户同时获益，但没有考虑光伏发电以及火电机组的污染物排放的问题。文献[10]通过价格机制引导电动汽车有序入网，以负荷方差和车主用电成本最低为目标，建立了风电与电动汽车入网调度模型，但没有涉及不同电价机制对用户负荷的影响。

综上所述，本文将电力需求侧资源与DEED相结合，以用户和车主利益为出发点，依据分时电价响应机制，从电力系统调度的经济性和环保性角度考虑，建立了车网互动、风光消纳、火电机组出力调度的多阶段多目标优化调度模型，将电力系统的供给侧资源与需求侧资源协同配合，以实现削峰填谷和提升可再生能源利用率的目的，最终使电力系统调度的经济和环境成本达到最低。采用基于求取帕累托最优前沿的NSGA-II算法[11-12]，结合模糊隶属函数、最小比耗量准则[13]，对多阶段模型进行求解。最终对3种不同的调度场景和4种不同的分时电价模式的调度结果进行对比分析。

1 用户负荷对分时电价响应下的模型

将分时电价响应下的用户负荷引入到含可再生能源和电动汽车入网的电力系统优化调度中，用户负荷曲线会根据所建立的目标函数做出相应变化[14]。但是，如果不能顾及用户的用电水平，最终会在得出最优调度方案时危及到用户的利益，使需求侧资源难以和可再生能源、常规发电形式协同配合参与调度。为此，综合考虑用户和电力系统双方的利益，制定适宜的分时电价和相应的调度方案，更准确地反映用户对电价的敏感程度，引入电量电价弹性公式。

式中：εst为电量需求弹性系数（用电需求系数）；ΔQdis为第i类用户用电量的相对增量；ΔPdit为第i类用户电价的相对增量；Q（0）dis为实施分时电价前的第i类用户第s时刻的用电负荷；P（0）dit为实施分时电价前第i类用户在第t时刻的用电电价。当s=t时，εst表示当前时段电价变化对当前用电量的影响（自弹性）；当s≠t时，εst表示当前时段电价变化对其他时段用电量的影响（交叉弹性）。由此用户在峰、平、谷3个时段内电量需求弹性矩阵如下所示。

2 计及需求响应的电动汽车和可再生能源多阶段DEED模型

在电力系统的常规调度方案中一般只考虑供给侧与需求侧的一方利益，调度优化方案较为单一。为了使需求侧资源与供给侧资源联合调度[15]，考虑双方利益，计及需求响应以确保用户合理用电和引导电动汽车适时适量充放电，进而消纳更多风力发电和光伏发电，降低火电机组的运行成本和污染物排放量，本文分别建立了参与调度的车网互动模型、风光消纳模型和火电机组的调度出力模型。

2.1 车网互动模型

等效负荷方差最小：

式中：Pload，t为在时刻t的用户负荷需求功率，与常规的用户负荷不同，此用户负荷随电价的变化而变化；Pve，t为电动汽车在时刻t的入网功率，正值代表充电，负值代表放电。

车主用电成本最低：

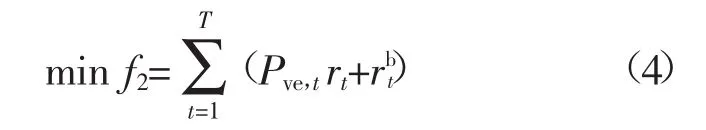
式中：rt代表在时刻t电动汽车入网充放电电价代表电动汽车电池在t时刻的损耗费用，其值为电动汽车电池充放电率乘以电动汽车入网的充放电电量[16-17]，即为了便于对比分析，设置电动汽车充放电电价与分时电价相等。

车网互动模型的约束条件如下。

1）电动汽车电池容量约束

式中：BOCt为t时刻电动汽车的存储电量；η为电动汽车充放电效率；Nve为参与系统调度的电动汽车总数量；BOCdrka，t为t时刻电动汽车行驶耗电量；Φpk，t为t时刻电动汽车的停驶概率；BOCve，av为相邻时间段内电动汽车的平均耗电量；BOCkm为电动汽车行驶每公里的平均耗电量；Vve为电动汽车平均行驶速度；.为保证电动汽车行驶的要求，设置电动汽车电池电量应在一定范围内，Φsd、Φsu分别为电动汽车荷电状态上下限系数，BOCve，max为电动汽车电池的最大储存容量。

2）电动汽车充放电功率约束

式中：Npk，t为t时刻处于停驶状态下的电动汽车数量；Pcha、Prel分别为电动汽车平均充放电功率。

2.2 风光发电消纳模型

在风、光发电消纳阶段，综合考虑风电和光伏发电入网对电力系统反调峰和调峰特性，以及可再生能源入网的间歇性，最大程度利用风光发电的同时，应考虑电力系统负荷的波动性。

等效负荷方差最小：

式中：Pwind，t、Psolar，t分别为风、光发电入网调度功率。

风、光发电消纳最大：

风、光发电功率受风电场、光伏发电场的装机容量的限制，约束条件为

式中：Pwind、Psolar分别为风、光发电场的总装机容量；分别为风、光发电预测功率。

2.3 火电机组调度出力模型

在计及需求响应下得到用户负荷曲线，在此次火电机组调度出力阶段，根据前两阶段得到的电动汽车充放电功率和风、光发电调度功率，综合考虑火电机组的经济和环境成本，确定火电机组的最优运行状态，得出火电机组的最优出力组合。

火电机组总运行成本最低：

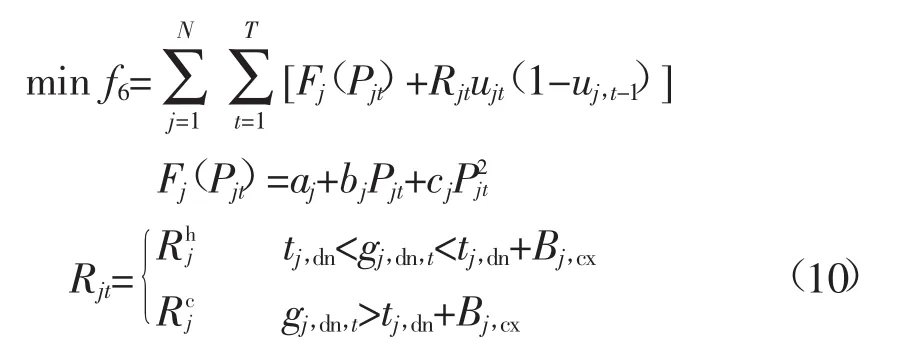
式中：Fj（Pjt）为火电机组的发电成本，aj、bj、cj分别为火电机组j的耗量特性系数；Rjt为火电机组j的启停维护成本；ujt为火电机组j在t时刻的运行状态，ujt为1代表火电机组j运行；ujt为0代表火电机组j停机；Rhj、Rcj分别为火电机组j的热启动成本和冷启动成本；tj，dn为火电机组j的最小容许停机时间；gj，dn，t为火电机组j在第t时刻的连续停机时间；Bj，cx为火电机组j的冷启动时间。

火电机组的污染物排放量最低：

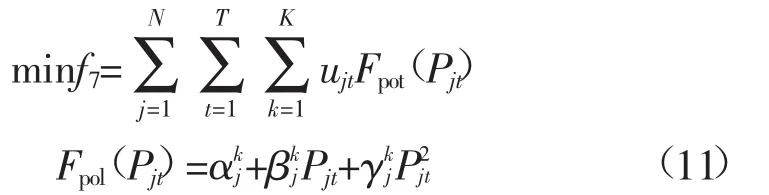
式中：Fpol（Pjt）为火电机组j的污染物排放量；k=1，2，3分别代表CO2、SO2和NOx；αkj、βkj和γkj分别表示火电机组污染物排放系数。

火电机组调度出力模型的约束条件如下。

1）电力系统功率平衡约束：

2）火电机组的出力上下限约束、爬坡约束、旋转备用约束、开停机约束：

式中：Pj，min、Pj，max分别为火电机组j的最小出力和最大出力；Φj，up为火电机组j的最大发电减量；Φj，dn为火电机组j的最大发电增量；Mt为电力系统在时刻t的旋转备用需求；gj，in，t为t时刻火电机组j的连续运行时间；tj，in为火电机组j的最小开机时间。

3 模型求解

3.1 算法求解策略

本文所建的是一个多阶段包含离散和连续变量的非线性多目标优化模型，用常规的优化算法对其求解很难得到精确解，因此本文采用基于求取帕累托解集的改进多目标遗传算法（NSGA-Ⅱ算法）。NSGA-Ⅱ算法是一种新型智能算法，该算法有易于理解、寻优速度快、精度更高、获得的帕累托多目标解更完美等一系列优点。本文采用算法的最大迭代次数为200，种群规模设为150，重复优化10次，变异概率为0.2，交叉概率0.8。

采用NSGA-Ⅱ算法对所建模型进行求解。首先根据电量需求弹性矩阵结合不同的分时电价模式，得出用户负荷；然后再依据NSGA-Ⅱ算法分别对车网互动模型、风光消纳模型进行多目标优化求解，得出各个时刻电动汽车充放电量和风、光发电消纳量；最终结合最优的风、光发电和电动汽车充放电，以最小比耗量准则，对火电机组的调度出力模型进行优化。具体各阶段的模型求解过程见流程图1。

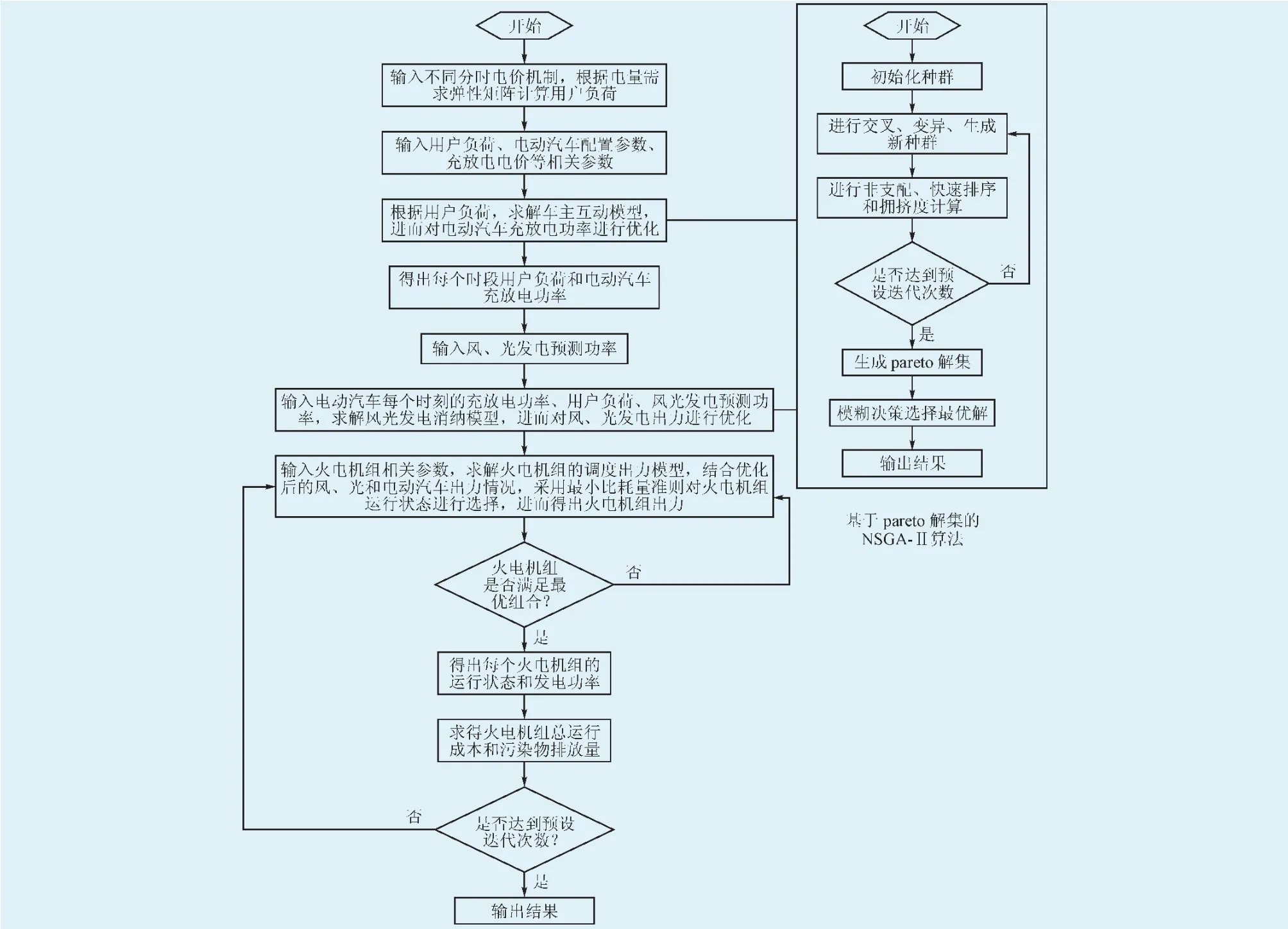
图1 求解流程图Fig.1 Flow chart of solution

3.2 火电机组组合

由于风力发电和光伏发电的间歇性、随机性，其入网调度后很难确定火电机组的运行状态及最优出力组合，本文将火电机组按照最小比耗量Cmin进行开停机顺序选择，进而确定火电机组的开停机顺序，优化火电机组的出力。相应处理如式（14）所示。

3.3 模糊求解

图2和图3分别为车网互动和风光消纳阶段得到的帕累托最优前沿，可以通过模糊决策理论[18-20]，从得出的帕累托解集中选择最优解。本文在求解车网互动模型和风光消纳模型时，分别采用降半梯度隶属函数和升半直线形隶属函数模糊化目标函数，当决策者对目标函数越满意，模糊隶属函数越接近于1，公式如式（15）所示。

图2 车网互动模型的帕累托最优前沿Fig.2 Pareto optimal frontier of vehicle grid interaction model

图3 风光消纳模型的帕累托最优前沿Fig.3 Pareto optimal front of wind photovoltaic consumptive model

式中：fi和Li分别为帕累托最优方案中目标函数i的取值和模糊隶属函数值；fi，min和fi，max分别为目标函数i的最小值和最大值。

4 算例分析

4.1 算例描述

为验证本文所构建模型的有效性，采用风力发电和光伏发电总装机容量分别为100 MW、20 MW，功率预测误差系数为0.1，以10台火电机组[21-22]为例进行多阶段仿真模拟，初始用户负荷见文献[21]，风光发电预测功率见图4，调度周期设为24 h。电动汽车的参数如下：电动汽车充放电功率为5 kW，充放电效率为0.95，平均行驶速度为40 km/h，电动汽车平均耗电量为0.2 kW·h/km，电池荷电状态上限参数设为0.8，下限参数为0.2，电池最大储存容量设为30 kW·h。电动汽车停驶概率[23]见图5。

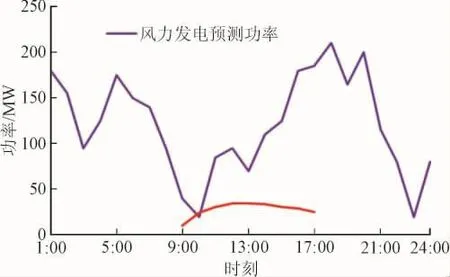
图4 风光发电预测功率Fig.4 Predictive value of wind photovoltaic power generation

电量需求弹性矩阵[24]为

平时段为6：00—8：00、18：00—19：00、22：00，谷时段为23：00—5：00，其他时段为峰时段；设置平时段电价为0.71元/（kW·h），峰、谷时段电价上下浮动比δp为30%，则峰、平、谷时段电价分别为0.71元/（kW·h）、0.923元/（kW·h）和0.497元/（kW·h）。不同模式的分时电价见表1。

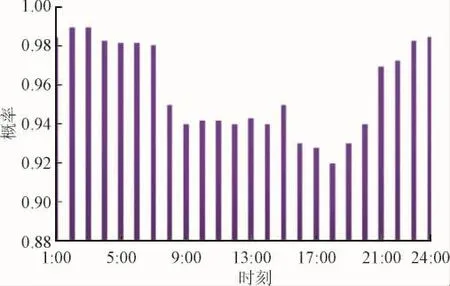
图5 电动汽车停驶概率Fig.5 Suspended probability of electric vehicles

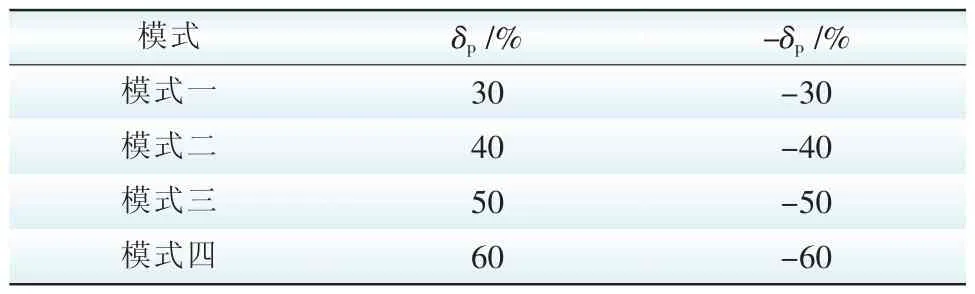
表1 不同模式的分时电价Tab.1 Different modes of time-of-use

4.2 计及需求响应的多阶段DEED结果对比分析

4.2.1 不同场景下的调度结果对比分析

为了充分验证各个阶段所构建模型的有效性和准确性，设置3个不同的调度场景，进行结果对比分析。场景1：不考虑用户利益仅考虑车主利益时的DEED场景。场景2：不考虑车主利益（电动汽车不参与入网调度）仅考虑用户利益时的DEED场景。场景3：既考虑车主和用户利益时的DEED场景。表2列出了不同调度场景下的车网互动模型、风光消纳模型和火电机组的调度出力模型的优化结果，图6给出了在考虑车主和用户利益时，光伏发电、风力发电和电动汽车入网调度功率分布。可知：在考虑车主和用户利益后，风电消纳量最大，光电消纳量变化不大，等效负荷方差、火电机组的总运行成本和污染物排放量最小，并且场景3比场景1和2的等效负荷方差分别减少了19 097.14 MW2、4 427.43 MW2，风电消纳量分别增加了13.26 MW、12.68 MW，火电机组总运行成本和污染物排放量分别减少了104 924元和295.55 t、91 528元和230.12 t。

在考虑车主利益时，车主在电价较高的负荷高峰时段选择放电，向电网送电，在电价较低的负荷低谷时段选择充电，进而消纳更多的风电，起到削峰填谷的作用，使等效负荷方差减小。随着风电消纳量和负荷峰谷差的减小，可以使火电机组的发电成本和启停维护成本进一步降低，由此使火电机组总运行成本和污染物排放量大大降低。

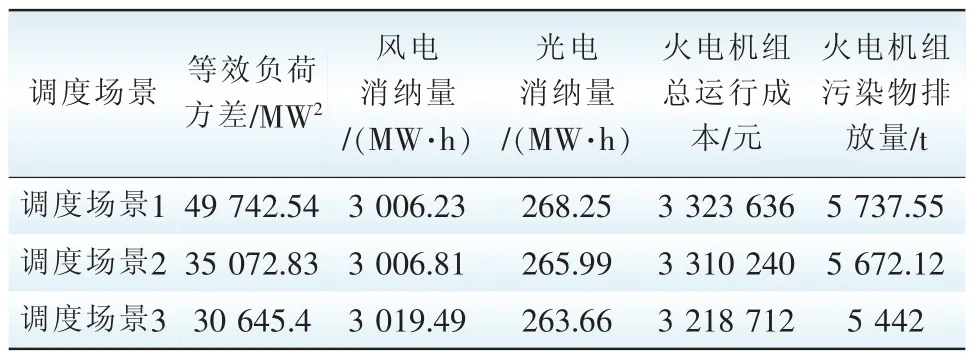
表2 不同调度场景下的优化结果Tab.2 Optimization results in different dispatching scenes

图6 光伏发电、风力发电、电动汽车入网调度功率分布Fig.6 Photovoltaic power generation，wind power，electric vehicles power gird dispatching distribution

在考虑需求侧资源时，用户在考虑自身利益前提下会根据电价的变化选择性用电，进而使等效负荷方差减小。在电价较低的负荷低谷时段，用户大量的用电促使了风电消纳能力的提升，进而使火电机组的总运行成本和污染物排放量降低。

在白天负荷高峰时段，光伏发电入网为火电机组分担出力，提升光电消纳能力，但在同时涉及车主和用户利益时，白天负荷高峰时，光电消纳量略微减小。

4.2.2 不同电价模式下的调度结果对比分析

图7为不同分时电价模式下的等效负荷曲线，图8为不同分时电价模式下电动汽车的充放电功率分布，可知：车主和用户对电价的敏感程度较强，当在电价较高的负荷高峰时段，车主会在满足自身行驶需求的前提下选择放电，用户会根据电价变化选择性用电，在电价较低的负荷低谷时段，车主会选择充电；因此合理的分时电价机制能够引导车主和用户参与电力系统入网调度，不仅可以增加用户和车主的利益，而且使电力系统调度更加安全、经济和环保，实现双赢。

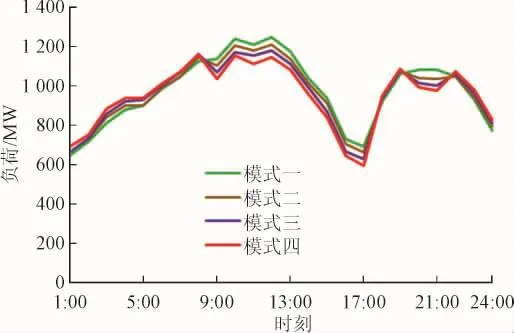
图7 不同分时电价模式下的等效负荷曲线Fig.7 Equivalent load curve in different modes of timeof-use

图8 不同分时电价模式下电动汽车充放电功率分布Fig.8 Power distribution of charging and discharging of electric vehicles of different modes of time-of-use

表3为不同分时电价模式下的优化结果。可知：随着峰、谷分时电价浮动幅度的扩大，风电消纳量逐渐增大，车主用电成本、等效负荷方差、火电机组总运行成本和污染物排放量逐渐减小。这是由于车主和用户会根据不同的分时电价模式选择性用电，在负荷高峰时车主选择放电，用户降低用电水平；在负荷低谷时，车主更多地选择充电，用户更多地选择用电，进而消纳更多风电，提升风电的利用率，由此进一步缩小负荷峰谷差，降低火电机组的经济和环境成本。在白天负荷高峰时，光伏发电入网起到“调峰”作用，但此时车主和用户用电需求降低，光电消纳量呈下降趋势，但变化量很小，对比于分时电价带来的其他优点可以忽略不计。

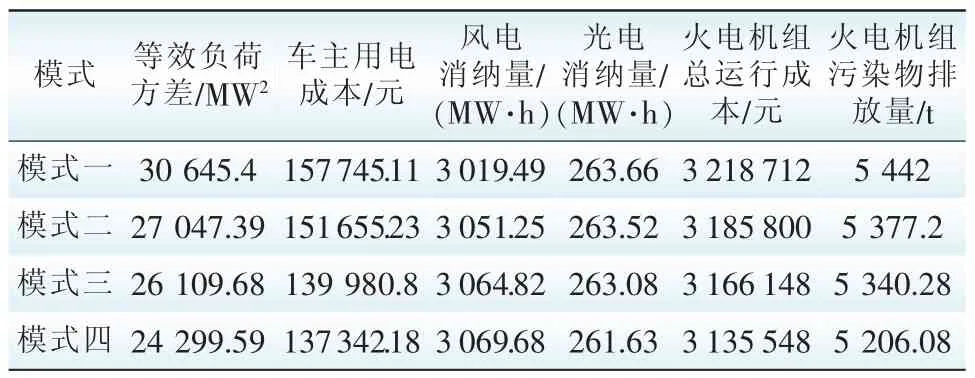
表3 不同分时电价模式下的优化结果Tab.3 Optimization results in different modes of time-of-use

5 结论

1）本文构建了计及需求响应的电动汽车和可再生能源多阶段DEED模型，通过制定合理的分时电价机制确定用户负荷曲线，以等效负荷方差最小、车主用电成本最低、风光消纳量最大等为目标，合理地利用需求侧资源配合可再生能源入网调度，最终得出最优的调度策略。

2）首先为了考虑用户对电价的敏感程度，利用电量需求弹性矩阵得出用户负荷曲线；然后采用NSGA-Ⅱ算法得出车网互动阶段和风光消纳阶段的帕累托最优前沿，为了避免决策的盲目性，配合模糊隶属度函数，选择最优解；最后配合最小比耗量准则确定火电机组的开机顺序，制定火电机组出力的最优组合，进而得出最优调度策略。

3）不同调度场景下的优化结果不同，同时考虑用户和车主利益能够使最终优化结果最理想。

4）不同的需求响应模式下，用户负荷曲线会发生相应变化，车主的用电成本、风光消纳量、火电机组的总运行成本和污染物排放量也不尽相同。合理地制定分时电价机制，能够使电力系统的调度既经济又环保，实现“双赢”。

[1]刘波，邱晓燕，韩轩，等.主动配电网分层分布控制模式切换研究[J].高压电器，2016，52（7）：68-74.LIU Bo，QIU Xiaoyan，HAN Xuan，et al.Research on hierarchical distributed control mode switching of active distribution network[J].High Voltage Apparatus，2016，52（7）：68-74.

[2]邬捷龙，杨健.能源互联网技术的现状及发展趋势研究[J].电网与清洁能源，2016，32（3）：8-12.WU Jielong，YANG Jian.Research on the current situation and development trend of the technology of energy internet[J].Power System and Clean Energy，2016，32（3）：8-12.

[3]郑建涛，徐越，许世森.太阳能-燃气联合循环发电技术[J].热力发电，2014，43（8）：24-28.ZHENG Jiantao，XU Yue，XU Shisen.An overview of in－tegrated solar combined cycle technology[J].Thermal Power Generation，2014，43（8）：24-28.

[4]吴晨曦.风光发电及电动汽车充放电随机性对配电系统的影响研究[D].杭州：浙江大学，2015.

[5]唐晓瑭，倪桦，王永生.电动汽车供电能源优化组合及智能充电策略[J].电力建设，2013，34（12）：111-115.TANG Xiaotang，NI Hua，WANG Yongsheng.Energy supply optimization and intelligent charging strategy of electric vehicles[J].Electric Power Construction，2013，34（12）：111-115.

[6]张智晟，温令云，李国，等.基于改进化学反应优化算法的电动汽车与可再生能源多目标协同调度[J].电网技术，2014，38（3）：633-637.ZHANG Zhisheng，WENG Lingyun，LI Guo，et al.Multiobjective coordinated scheduling of electric vehicles and renewable generation based on improved chemical reaction optimization algorithm[J].Power System Technology，2014，38（3）：633-637.

[7]黄晓倩，汪沨，谭阳红，等.考虑V2G模式的电动汽车与可再生能源协同调度[J].工程设计学报，2016，23（1）：67-73.HUANG Xiaoqian，WANG Feng，TAN Yanghong，et al.Coordinated scheduling of electric vehicles and renewable generation considering vehicle-to-grid mode[J].Journal of Engineering Design，2016，23（1）：67-73.

[8]朱永胜，王杰，瞿博阳，等.含电动汽车的电力系统动态环境经济调度[J].电力自动化设备，2016，36（10）：16-23.ZHU Yongsheng，WANG Jie，QU Boyang，et al.Dynamic environmental and economic dispatch of power system with EVs[J].Automation of Electric Power Systems，2016，36（10）：16-23.

[9]鞠立伟，秦超，吴鸿亮，等.计及多类型需求响应的风电消纳随机优化调度模型[J].电网技术，2015，39（7）：1839-1846.JU Liwei，QIN Chao，WU Hongliang，et al.Wind power accommodation stochastic optimization model with multitype demand response[J].Power System Technology，2015，39（7）：1839-1846.

[10]侯建朝，胡群丰，谭忠富.计及需求响应的风电-电动汽车协同调度多目标优化模型[J].电力自动化设备，2016，36（7）：22-27.HOU Jianzhao，HU Qunfeng，TAN Zhongfu.Multi objective optimization model of collaborative WP-EV dispatch consdering demand response[J].Automation of Electric Power Systems，2016，36（7）：22-27.

[11]AHMED F，DEB K.Multi-objective optimal path planning using elitist non-dominated sorting genetic algorithms[J].Soft Computing，2013，17（7）：1283-1299.

[12]钱国超，马御棠，刘渝根，等.遗传算法在接地网腐蚀故障诊断中的应用研究[J].电瓷避雷器，2014（2）：52-59，65.QIAN Guochao，MA Yutang，LIU Yugen，et al.Research on the application of genetic algorithm in fault diagnosis of grounding grid corrosion[J].Insulators and Surge Arresters，2014（2）：52-59，65.

[13]王开艳，罗先觉，吴玲，等.清洁能源优先的风-水-火电力系统联合优化调度[J].中国电机工程学报，2013，33（13）：27-35.WANG Kaiyan，LUO Xianjue，WU Ling，et al.Optimal dispatch of wind-hydro-thermal power system with priority given to clean energy[J].Proceeding of the CSEE，2013，33（13）：27-3.

[14]李浩闪，李燕青.分时电价下考虑用户侧响应的日前调度计划建模与分析[J].华东电力，2014，42（2）：314-318.LI Haoshan，LI Yanqing.Day-ahead generation dispacth modeling and analysis considering demand response under time-of-use price[J].East China Electric Power，2014，42（2）：314-318.

[15]刘旭，杨德友，孟涛，等.计及需求响应的含风电场日前两阶段动态环境经济调度[J].电力建设，2016，37（9）：146-154.LIU Xu，YANG Deyou，MENG Tao，et al.Day-ahead two-stage dynamic economic emission dispatching in wind power integrated system incorporating demand response[J].Electric Power Construction，2016，37（9）：146-154.

[16]WHITE C D，ZHANG K M.Using vehicle-to-grid technology for frequency regulation and peak-load reduction[J].Journal of Power Sources，2011，196（8）：3972-3980.

[17]杨甲甲，赵俊华，文福拴，等.含电动汽车和风电机组的虚拟发电厂竞价策略[J].电力系统自动化，2014，38（13）：92-102.YANG Jiajia，ZHAO Junhua，WEN Fushuan，et al.Development of bidding strategies for virtual power plants considering uncertain outputs from plug-in electric vehicles and wind generators[J].Automation of Electric Power Systems，2014，38（13）：92-102.

[18]鞠立伟，李欢欢，陈致宏，等.基于两步制自适应求解算法的风电-电动汽车多种并网模式效益对比分析模型[J].电网技术，2014，38（6）：1492-1498.JU Liwei，LI Huanhuan，CHEN Zhihong，et al.A benefit contrastive analysis model of multi grid-connected modes for wind power and plug-in hybrid electric vehicles based on two-step adaptive solving algorithm[J].Power System Technology，2014，38（6）：1492-1498.

[19]刘柏良，黄学良，李军，等.含分布式电源及电动汽车充电站的配电网多目标规划研究[J].电网技术，2015，39（2）：450-456.LIU Bailiang，HUANG Xueliang，LI Jun，et al.Multiobjective planning of distribution network containing distributed generation and electric vehicle charging stations[J].Power System Technology，2015，39（2）：450-456.

[20]李军，颜辉，张仰飞，等.基于改进萤火虫算法的农村配电网分布式电源优化配置[J].电力电容器与无功补偿，2016，37（6）：82-87.LI Jun，YAN Hui，ZHANG Yangfei，et al.Distribution power optimization configuration of rural distribution grid based on improved firefly algorithm[J].Power Capacitor Reactive Power Compensation，2016，37（6）：82-87.

[21]TING T O，RAO M V C，LOO C K.A novel approach for unit commitment problem via an effective hybrid particle swarmoptimization[J].IEEETransactionson PowerSystems，2006，21（1）：411-418.

[22]王抒祥.减排约束下电力资源综合利用优化模型与方法研究[D].北京：华北电力大学，2013.

[23]王亦，吴俊明，翟云峰，等.考虑大规模风电和电动汽车入网的协同优化调度[J].电力科学与工程，2015，31（4）：11-17.WANG Yi，WU Junming，ZHAI Yunfeng，et al.Synergistic optimization scheduling considering large-scale wind power and electric vehicles integration[J].Electric Power Science and Engineering，2015，31（4）：11-17.

[24]谭忠富，陈广娟，赵建保，等.以节能调度为导向的发电侧与售电侧峰谷分时电价联合优化模型[J].中国电机工程学报，2009，29（1）：55-62.TAN Zhongfu，CHEN Guangjuan，ZHAO Jianbao，et al.Optimization model for designing peak-valley time-of-use power price of generation side and sale side at the direction of energy conservation dispatch[J].Proceeding of the CSEE，2009，29（1）：55-62.

Multi-Stage Dynamic Economic Emission Dispatch Optimization Model of Electric Vehicles and Renewable Energy Incorporating Demand Response

HOU Jianchao，HOU Pengwang，SUN Bo
（School of Economics and Management，Shanghai University of Electric Power，Shanghai 200090，China）

This paper presents an related to demand response of electric vehicles and renewable energy multi stage grid dispatchingmodel.Firstly，adopting time-of-use price mechanism to guide the user using electricity reasonably to obtain accurate user load curve.Then in the vehicles gridinteracting stage and wind and photovoltaic consumptive scenery stage，for the purpose of smoothing system load fluctuation，respectively taking the owner of vehicles’lowest cost of using electricity，wind and photovoltaic power consumption as the goal，applying the NSGA-II algorithm to obtain the pareto optimal frontier and fuzzy membership function cope with the electric vehicles charging and discharging，wind power and photovoltaic power output.Finally，in the power generation dispatching stage，taking the thermal power units’economic and environmental costs as the goaloptimize the output of thermal power units.The simulation results show that the reasonable mechanism of time-of-use price can change the owner of the vehicles charging and discharging behavior and users’using electricity behavior，reducing the peak load，improving wind and photovoltaicpower consumptive capacity，reducing the total cost of operation and the pollutant emissions of thermal power units.

electrical vehicles；time-of-use price；the consumption of wind and photovoltaicpower；NSGA-II；demand response

提出了一种计及需求响应的电动汽车和可再生能源多阶段入网调度模型，首先通过分时电价机制引导用户合理用电，得出精确的用户负荷曲线；然后在车网互动阶段和风光消纳阶段，在以平滑系统负荷波动为目的的基础上，分别以车主用电成本最低和风、光发电消纳最大为目标，采用基于求取帕累托最优前沿的NSGA-II算法和模糊隶属函数对电动汽车充放电、风力发电和光伏发电出力进行优化；最后在火电机组调度出力阶段，以火电机组经济和环境成本最低为目标，对火电机组出力进行优化。算例结果表明：合理的分时电价机制能够改变车主的充放电行为和用户的用电行为，减小负荷峰谷差，提升风、光发电消纳能力，减小火电机组的总运行成本和污染物排放量。

电动汽车；分时电价；风光消纳；NSGA-II；需求响应

1674-3814（2017）09-0104-09

TM734

A

教育部人文社会科学研究青年基金（15YJCZH147）；上海市社科规划一般课题（2015BGL002）。

Project Supported by the Youth Fund of Humanities and Social Sciences Research from the Ministry of Education（15YJCZH147）；General Topics of Social Science Planning in Shanghai（2015BGL002）.

2016-12-06。

侯建朝（1973—），男，博士，副教授，中国社会科学院财经战略研究院博士后，主要从事电力能源经济及智能电网需求侧管理的研究工作；

侯鹏旺（1990—），男，硕士研究生，主要研究方向为电动汽车与需求侧管理；

孙 波（1982—），女，副教授，博士，主要研究方向为最优化及智能电网需求侧管理。

（编辑 冯露）