基于隐马尔可夫模型的电力系统连锁故障预测

丁岩，郭和强，王利利，李秋燕，孙义豪，关朝杰

（1.国网河南省电力公司经济技术研究院，河南郑州 450001；2.天津天大求实电力新技术股份有限公司，天津 300001）

基于隐马尔可夫模型的电力系统连锁故障预测

丁岩1，郭和强2，王利利1，李秋燕1，孙义豪1，关朝杰1

（1.国网河南省电力公司经济技术研究院，河南郑州 450001；2.天津天大求实电力新技术股份有限公司，天津 300001）

在国民经济中，电力的地位异常重要，社会的发展以及电网的扩大都离不开供电的可靠性。然而，操作不当、电网结构不合理、短路（或断路）等故障以及其他外界因素的干扰，都可能导致电力系统事故，甚至发生大面积停电[1]。因此，对电力系统连锁故障的预测和诊断有助于电力系统可靠性的提高以及停电损失的减少[2]。一旦发生电力系统大事故或者大面积停电，将会给经济带来重大损失，甚至给社会带来难以预想的重大影响[3]。

随着科技的迅速发展，电路的集成度越来越高，因此电力系统具有更加复杂的结构。电力系统中任何一级发生故障，都会产生很大的影响，特别是连锁故障的发生，影响程度会更大。虽然我们无法避免单个元件发生故障，但是，可以通过各种预测和技术手段，将连锁故障降低到最低。目前，在国外关于连锁故障预测的相关研究已经很多，例如蒙特卡罗抽样法、随机模拟法或N-1判据等方法[4-5]。面对连锁故障或多重故障等较难处理的情况，可以采用N-1判据法来处理；对于不确定事件，可以基于蒙特卡罗抽样的随机模拟来预测初始故障。

在连锁故障预测的研究领域中，解决故障预测主要包括两种方法：一是基于人工智能的方法，二是基于复杂网络理论的方法。人工智能方法又可以分为不同的模型，例如OPA模型、CASCADE模型以及隐藏故障模型等，这种方法的特点是对电力系统的演化过程较为简洁，但是人工智能的故障预测还存在着不足，如果某条线路停止对状态更新，那么这种方法对潮流等方面的模拟将会脱离实际电力系统的运行状态。随着网络理论复杂程度的不断增加，小世界模型实现了对复杂网络理论的连锁故障预测，这种模型主要是从网络结构角度来研究，分析当电力网络遭受各种不同攻击时，电网所能承受的最大限度。此外，如果电力网络被攻击，这种攻击可能会造成连锁故障等问题。在连锁故障预测方面，问题比较复杂，常常存在着隐藏状态，为了能够清晰地将观测状态与隐藏状态的对应关系描述出来，可采用隐马尔可夫模型。

1 隐马尔可夫模型的基本理论

1.1 马尔可夫链

在状态空间和时间参数均为离散的条件下，马尔可夫过程也可以称为马尔可夫链。在马尔可夫过程中，随机过程的将来状态只是与当前状态有关，而与过去状态无关。在数学领域中，马尔可夫链的定义如下：

假设，存在一个随机过程X（t），t∈T，对于S1，S2，…，SN等N个互不相同的状态，其中n=1，2，…，n∈R，X（t）在t时刻可能的状态一定是N个互不相同的状态中的一个，且X（t）只在t1，t2，…，tn个可列个时刻（即时间参数为离散的）发生状态转移。

马尔可夫链描述了随机过程在时间参数为离散值的条件下，随机过程X（t）在不同时刻所对应状态可能发生的概率。随机状态发生概率如下：

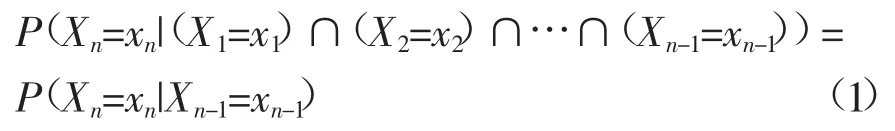
其中，将来状态（t=n时刻）的随机变量值Xn仅仅和当前状态（t=n－1时刻）的随机变量的取值Xn－1有关。状态i到状态j的一步转移概率的表达式如下：

其中，当状态i属于离散空间B时，有：

马尔可夫链具有平稳性、周期性、互通性、普遍性以及常返性等特征。在理想情况下，每一个可以观测到的实际存在的事件，都可以严格地对应马尔可夫链中的一个状态。利用马尔可夫链的性质，在不同的领域中，对不同事件的发生概率进行比较分析，从而可为未来的良好发展提供有力的决策依据。

1.2 隐马尔可夫模型的基本概念

与理想的马尔可夫链的条件不同，在实际分析时，存在着一些无法被观测到的确切状态，将这些无法观测的状态看作另一随机过程，因此，隐马尔可夫模型（HMM）是一个双重随机过程。

隐马尔可夫模型的双重随机过程可以简单地分为马尔可夫链和观测过程[6]。作为第一个随机过程，马尔可夫链描述不同状态之间的转化过程，该随机过程通常用转移概率矩阵来描述。而作为隐马尔可夫模型的第二个随机过程，观测过程主要是描述状态序列与观测序列之间的关系，该随机过程通常用观察值概率矩阵描述。

在隐马尔可夫模型中，状态除了具有不确定性以外，甚至还会有隐藏性。只有通过服从一定规律的随机观测状态，才能将这些不确定的、隐藏的内在状态体现出来。因此，从观测者的角度而言，只能看到观测值，这是因为隐马尔可夫模型中每个时刻的观测值与状态不具备一一对应的映射关系，而是利用一组概率分布来联系观测到的事件与状态。基于马尔可夫链，增加另一随机过程来描述隐藏状态的存在及其特性，该模型称之为隐马尔可夫模型。隐马尔可夫模型的原理示意如图1所示。

图1 隐马尔可夫模型的原理图Fig.1 Schematic diagram of the hidden Markov model

图1中，π为初始概率分布，τ为状态空间维数，Τ为观测空间维数。作为马尔可夫模型的扩展，隐马尔可夫模型主要由5组参数决定，分别是模型的状态数目N，模型每个状态对应的观测特征数目M，状态转移概率分布A，观测特征在各个状态的观测概率分布B以及初始化状态概率分布π。因此，一个隐马尔可夫模型可以记作λ=（N，M，π，A，B），简写为λ=（π，A，B）[7]，典型的隐马尔可夫模型如图2所示。

图2 典型的隐马尔可夫模型Fig.2 Typical hidden Markov model

对参数N，隐马尔可夫模型的实际物理状态是无法直接观测到的，只能通过观测值序列对 该物理状态进行估计。在隐马尔可夫模型中，已知观测序列中各种可能隐藏状态序列可以利用观测序列和观测值概率进行推测。当然，不同观测序列的出现概率也可以由观测序列和观测值概率推测出来。隐马尔可夫模型的隐藏状态序列具有随机性和马尔可夫性，隐藏状态也可能对应着多个观测值概率。

在隐马尔可夫模型中，需要统计每个状态对应的观测特征数目。而观测特征添加了物理系统的输出，在任一时刻，都可能观测到系统的多种特征，这些特征可以用集合的方式表示，即V={v1，v2，…，vM}。在某一段时间内，利用上述的观测特征，便可以得到一组观测序列，记作O={O1，O2，…，OT}，其中ot对应着t时刻的集合V中的某一观测值对象[7]。

状态转移概率分布的表达式如公式（4）所示：

其中，

初始概率分布π的表达式如下：

其中，

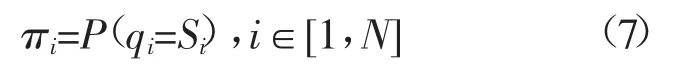
1.3 隐马尔可夫模型解决的问题及其相应算法

隐马尔可夫模型主要解决的基本问题包括解码、评估和学习等3个[8-9]。首先，用一些算法（如Viterbi算法）进行解码。解码过程就是根据已知的模型以及实验得到的观测序列，通过求解找出这组序列中发生最大概率的状态。然后，利用前向－后向算法进行问题评估，即通过已知模型和观测序列求出该序列在模型下出现的概率。最后，利用Baum-Welch算法对大量的观测序列进行训练，从而得到一组模型参数。

隐马尔可夫模型中三大算法（前向－后向算法、Viterbi算法和Baum-Welch算法）之间的关系[10]如图3所示。

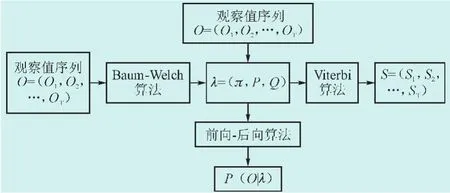
图3 隐马尔可夫模型中三大算法关系图Fig.3 Analysis of three algorithms in hidden Markov model

1.3.1 前向-后向算法

为解决评估问题，作为一种高效算法，前向-后向算法用来求解P（O|λ）的值。在解决概率推理问题的方法中，这是一种最为常用的方法。直观来看，该算法大致分为两个部分，即前向、后向。

在前向算法中，首先需要定义前向变量，如：

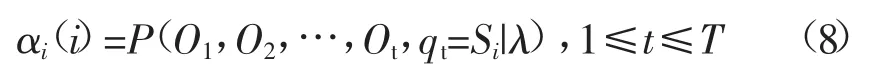
然后，将前向变量进行初始化，之后依次是递归和终结。递归指的是针对每个时刻和每个状态的顺序来建立两个前向变量t时刻与t+1时刻之间的关系，从而得到任一时刻前向变量值。这种前向算法的优点在于复杂度小，它将N（N+1）（T－1）+N次乘法简化为N（N－1）（T－1）次加法，这种算法可以看作是一种典型的格型结构。

后向算法与前向算法相似，也是一种典型的格型结构，其主要步骤依次为：定义后向变量，初始化，递归，终结。在后向算法中，其计算量略大于前向算法，大约在N2T量级。在实际应用中，后向算法所求出的值通常接近于零，因此，在计算过程中常常利用归一化和对数形式求解。

1.3.2 Viterbi算法

Viterbi算法主要是用来解决当观察值序列和模型给定时，在最佳的意义上确定一个状态序列。例如，已知给定的观察值序列和模型分别为O=（O1，O2，…，Ot）和λ=（π，A，B），确定状态序列Q=（q1，q2，…，qt）。在不同情况下，“最佳”的定义也有所不同，而本文中的“最佳”指的是最大的状态序列Q=（q1，q2，…，qt）。

在Viterbi算法中，求解最佳状态序列的主要步骤与前向-后向算法相类似，求解过程如下：初始化，递归，终结和求得状态序列。初始化过程中，可以根据变量定义得到初始化条件。当时间达到最大时，Viterbi算法终止，与此同时解得P*的极大值。

从求解过程不难看出，Viterbi算法也是一种典型的格型结构。它与前向－后向算法的主要区别在于Viterbi算法是求解以前状态的最大值，而前向-后向算法主要是利用求和过程。因此，实际应用时，通常是利用Viterbi算法求解P*。

1.3.3 Baum-Welch算法

Baum-Welch算法，即期望修正法，广泛应用于解决学习问题。Baum-Welch算法的基本原理是利用迭代更新来得到模型参数的局部最优解[8]。首先对隐马尔可夫模型中的各参数π、A、B，即λ=（π，A，B），进行参数重估，得到新的参数模型，然后对隐马尔可夫模型进行迭代更新，最后得到模型参数的局部最优解。

Baum-Welch算法的求解过程也与前两种算法类似，主要步骤依次为：初始化，更新模型参数、终止。所谓的初始化就是根据变量的定义给定模型参数λ=（π，A，B），得到初始条件。在进行参数重估之前，还需要定义两个参数ζt（i，j）和γt（i）。其中ζt（i，j）表示t时刻为Si，t+1时刻为Sj的概率；γt（i）表示，在已知观测序列的条件下，t时刻的状态为Si的概率。利用公式对上述两个参数ζt（i，j）和γt（i）进行计算，并将隐马尔可夫模型中的参数进行重新估计，从而得到新的隐马尔可夫模型参数λ′=（π′，A′，B′）。重复迭代计算Q（λ，λ′），直到满足迭代次数或连续两次概率的增量比设定值小。

1.4 隐马尔可夫模型的分类

隐马尔可夫模型的许多特性都可以用来解决现实生活中的许多实际问题，其分类可以有多种。从处理的数据类型角度来看，隐马尔可夫模型可以分为离散型和连续型。在现实生活中，许多实际的物理量都是连续的，也可认为这需要处理的数据也是连续的，例如语音信号识别，股票几个时间序列预测，人脸识别和人体运动识别等。当然，在现实世界中，也有少数数据是离散的，因此观测值属于离散量，故称为离散型马尔可夫模型。

根据马尔可夫模型实现方式，又可分为遍历型马尔可夫模型、自回归马尔可夫模型、输入输出马尔可夫模型、因子马尔可夫模型和耦合马尔可夫模型[10]。其中，耦合隐马尔可夫模型是指将传统隐马尔可夫模型中的单条马尔可夫链扩展为多条马尔可夫链。耦合隐马尔可夫模型中，虽然各马尔可夫链在时间上可能发生交叉的情况，但是每条马尔可夫链自身是相对独立的，生成的观察序列也是互不影响的。实际上，可以将耦合隐马尔可夫模型看作在多个隐马尔可夫序列之间引入耦合条件概率从而得到多马尔可夫模型[10]。

2 隐马尔可夫模型在电力系统连锁故障预测中的应用

在电力系统中，如果某一级线路发生故障，将会引起下一级的故障。如果能够及时的将单一的故障清除，将不会导致整个系统的崩溃。然而，在某段时间内，如果大量元件因为产生过载保护动作而停止工作，那么，电力系统将会快速的进入崩溃状态。因此，将会出现大面积的停电，给经济带来巨大的损失。利用隐马尔可夫模型，对电力系统中的安全隐患进行预测，大大降低了电力系统事故甚至大面积停电等发生的概率。此外，实验证明，利用隐马尔可夫模型对电力系统进行连锁故障预测，其准确率通常在97.5%左右[11]。

2.1 基于马尔可夫模型连锁故障预测的流程

在利用马尔可夫模型进行电力系统连锁故障预测的过程中，首先需要选择一条故障路线并判断该故障路线的故障原因，该故障原因可定义为故障i。然后任一选取一条路径n作为研究对象，计算线路n发生初始故障的概率P。通过一系列的条件判断后，计算线路n的综合状态转移概率。然后，将该计算结果代入马尔可夫链的预测模型中，从而计算线路的故障概率。通过计算比较，选出故障概率值最大的线路作为当前线路的下一级故障线路，并对整个电力系统进行脆弱性分析。重复上述的预测过程，对电路系统的故障预测进行逐级分析。

通过比较逐级扫描前一级线路切除后其他线路发生故障的概率值，选出最大概率值所对应的线路，利用这种方式，对每条路径的发生故障的概率进行综合评价，针对不同故障概率值，提前采取相关的应对措施，从而减少电力系统连锁故障的发生。

2.2 实例分析

在电力系统中，因潮流转移而引发的线路过载是发生连锁故障的主要原因。此外，由于保护或断路器的错误动作以及系统硬件失效等其他小概率事件，系统状态也会加速恶化，最终导致电力系统崩溃，发生大面积停电事故。

为更好地预测电力系统故障，需要对由潮流转移导致的状态转移概率进行分析和计算。系统的运行状态不同，潮流转移引起的状态转移概率也会有所不同。

以IEEE 10机39节点的系统为例，利用隐马尔可夫模型对电力系统故障进行预测，IEEE 10机39节点系统如图4所示。

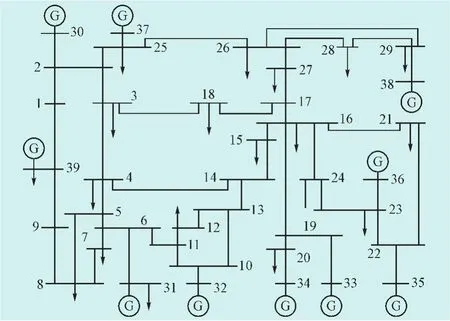
图4 IEEE 10机39节点系统Fig.4 IEEE 10 machine 39 node system

如果该系统发生m级电路故障，根据马尔可夫模型连锁故障预测的流程，不难算出故障线路以外的综合状态转移概率。如果上一级在同一线上发生故障，该线路成为下一级连锁故障的可能性将会受转移概率的影响。一般来讲，转移概率的值越大，该线路越容易成为下一级的故障线路。因此，通过对发生故障以外的线路的综合状态转移概率进行比较，选出概率值最大的那一条作为次级连锁故障。

为计算图4中发生故障时综合状态转移概率（Pm_k），我们做出如下假设：

1）故障级数m=8；

2）将m=2级故障作为前一级故障可能性最大的两条路线；

3）出于某些原因，线路13-14发生故障。

当m=8时，线路4-14和线路3-4的综合状态转移概率分别为0.702 5和0.862 4；当m=7时，线路15-16和线路29-38的综合状态转移概率分别为0.843 4和0.983 1；当m=6时，线路22-23和线路16-19的综合状态转移概率分别为0.683和0.905 8。

由此可见，不同的故障路径所对应的系统脆弱性指标值有所不同。电力系统脆弱性指标是对系统承受干扰或故障的能力的描述，主要包括：负荷损失指标、输电能力下降指标、最大联通与比率指标。以系统脆弱性指标作为辅助依据，有利于运行人员对可能发生的连锁故障进行整体上的掌控。当然，在实际应用中，发生故障的线路不一定是故障概率值最大的路径。因此，在对实际电力系统进行连锁故障预测时，还需考虑其他故障概率较大路径的影响。

3 结论

电力系统的连锁故障将会导致大面积停电事故，给人们的生活带来很多不便。为了能够清晰地将故障观测状态与隐藏状态的对应关系描述出来，通过建立隐马尔可夫模型，能够有效地预测下一级故障的发生概率。本文对隐马尔可夫模型的基本理论和模型构建进行了总结和分析，通过工程实例，进一步分析了基于隐马尔可夫模型进行电力系统连锁故障预测需要考虑的因素，并得出如下结论：

1）在电力系统中，连锁故障之间的每一级都是相互影响的，每级之间都存在着某种对应关系。因此，为了能准确地预测出次级发生故障的概率，需要充分地考虑前后级故障之间的状态转移关系。

2）利用隐马尔可夫模型对电力系统进行连锁故障预测，能够准确地计算出状态转移概率和断路器异常动作概率，从而逐级预测故障的发生。

3）对于电力系统中各模块的退化状态，隐马尔可夫模型可以准确的识别出来，有效地预测连锁故障发生概率。例如在实例分析中，当线路13-14发生故障退出运行后，通过对各级的综合状态转移概率来预测下级发生故障的可能性，从而有效地控制连锁故障的发生。

[1]程林，刘满君，易俊，等.基于运行可靠性模型的连锁故障模拟及薄弱环节分析 [J].电网技术.2016，40（5）：1488-1494.CHENG Lin，LIU Manjun，YI Jun，et al.Fuzzy-chain simulation and weak link analysis based on operational reliability model[J].Power System Technology，2016，40（5）：1488-1494.

[2]吴文可.电力系统故障诊断模型与事故处理辅助决策方法[D].广州：华南理工大学，2013.

[3]程林，刘满君，何剑，等.基于马尔可夫过程的电力系统连锁故障解析模型及概率计算方法[J].电网技术，2017，41（1）：130-136.CHENG Lin，LIU Manjun，HE Jian，et al.An analytical model and probability calculation method for cascading failures in power system[J].Power System Technology，2017，41（1）：130-136.

[4]吴文可，文福拴，薛禹胜，等.基于马尔可夫链的电力系统连锁故障预测 [J].电力系统自动化，2013，37（5）：29-37.WU Wenke，WEN Fushuan，XUE Yusheng，et al.A Markov chain based model for forecasting power system cascading failures[J].Automation of Electric Power Systems 2013，37（5）：29-37.

[5]张桦.配电系统可靠性预测模型及其算法研究 [D].重庆：重庆大学，2016.

[6]夏丽莎.基于隐马尔可夫模型的故障诊断及相关算法研究[D].武汉：华中科技大学，2014.

[7]田沿平，叶晓慧，金川，等.耦合隐马尔可夫在模拟电路故障预测中的应用[J].电子测量技术，2014，37（10）：135-138.TIAN Yanping，YE Xiaohui，JIN Chuan，et al.Application of coupled hidden Markov model in analog circuit fault prediction[J].Electronic Measurement Technology，2014，37（10）：135-138.

[8]刘韬.基于隐马尔可夫模型与信息融合的设备故障诊断与性能退化评估研究[D].上海：上海交通大学，2014.

[9]胡为，高雷，傅莉.基于最优阶次HMM的电机故障诊断方法研究[J].仪器仪表学报，2013，34（3）：524-530.HU Wei， GAO Lei， FU Li.Research on motor fault detection method based on optimal order hidden Markov model[J].Chinese Journal of Scientific Instrument，2013，34（3）：524-530.

[10]龙百元.基于层次分析法和隐马尔可夫模型的风险评估方法研究[D].长沙：湖南大学，2007.

[11]柳楠.基于隐马尔可夫模型的航空机械系统故障诊断算法设计[J].现代工业经济和信息化，2016，6（5）：44-45.LIU Nan.The design of aviation mechanical system fault diagnosis algorithm based on hidden Markov model[J].Modern Industrial Economy and Information Technology，2016，6（5）：44-45.

Power System Cascading Failure Prediction Based on Hidden Markov Model

DING Yan1，GUO Heqiang2，WANG Lili1，LI Qiuyan1，SUN Yihao1，GUAN Chaojie1
（1.State Grid Henan Economic Research Institute，Zhengzhou 450001，Henan，China；2.Tianjin Tianda Qiushi Electric Power High Technology Co.，Ltd.，Tianjin 300001，China）

In recent years，the power system is gradually developing toward a complex，integrated and intelligent system.Cascading failures of power systems will result in blackouts in large areas and brings a lot of inconvenience to people′s lives.Therefore，prediction of cascading failures is getting more and more important in the field of power systems.However，because of complexity of the network，correlation between faults and uncertainty of the power system，the existing fault prediction methods are not applicable any more.To this end，this paper presents a cascading failure prediction method based on Markoff model.Using the hidden Markov model to predict the fault of the power system，it is possible to accurately calculate the state transition probability or the abnormal probability of the circuit breaker，so as to predict occurrence of the fault step by step.The hidden Markov model can identify the degradation state of each module in power systems，and effectively predict the probability of cascading failures.

power system;cascading failure;hidden Markov;faultprediction

近年来电力系统逐渐向复杂化、集成化和智能化的方向发展。电力系统的连锁故障将会导致大面积停电事故，给人们的生活带来很多不便。因此，在电力系统领域，对连锁故障的预测地位日益凸显。然而，网络的复杂性、故障间的关联性和系统的不确定性使得现有的故障预测方法并不适用。因此，提出基于隐马尔可夫模型对电力系统连锁故障进行预测。该模型能够准确地计算出状态转移概率或断路器异常动作概率，从而逐级预测故障的发生。对于电力系统中各模块的退化状态，隐马尔可夫模型可以准确地识别出来，有效地预测连锁故障发生概率。

电力系统；连锁故障；隐马尔可夫；故障预测

1674-3814（2017）09-0093-06

TM76

A

国家自然科学基金资助项目（51190103）；国家电网公司科技资助项目（5217L0150005）。

Project Supported by the National Natural Science Foundation of China（51190103）；the Science and Technology Program of State Grid Corporation of China（5217L0150005）.

2016-10-25。

丁 岩（1988—），男，工程师，本科学历，研究方向：电力系统规划设计。

（编辑 李沈）