从Bloch空间到加权型空间上二阶微分算子与乘子的积
2018-01-02李涛
李 涛
(连云港开放大学,江苏 连云港 222006)
从Bloch空间到加权型空间上二阶微分算子与乘子的积
李 涛
(连云港开放大学,江苏 连云港 222006)
文中讨论了单位圆盘上Bloch到加权型空间上的算子D2Mu的有界性和紧性,得到从Bloch空间到加权型空间上的算子D2Mu是有界算子以及紧算子的充要条件.
二阶微分算子;乘子;Bloch 空间;加权型空间 MR(2000)主题分类:47B38;47B33;30D45;46E15
1 引言
文献[1],[2]分别研究了复合算子和复合算子与一阶微分算子的乘积;文献[3],[4]中研究了一阶微分算子与其它算子的乘积;文献[5]研究微分算子与复合算子的乘积,文献[6],[7]研究了Bloch空间,文献[8]研究了有界解析函数空间上二阶微分算子与乘子的积.文中讨论了二阶微分算子与加权复合算子的积:

得到了从Bloch空间到加权型空间上的算子的有界算子和紧算子的充要条件.文中字母C是一个正常数,不同的地方可以不同.
2 预备引理
引理2.1[5,6]如果,那么对于任意正整数n,

引理 2.2[5]如果f∈B,那么
由紧算子定义以及Montel定理,可得出下面的引理.
引理 2.3如果u∈H(Δ),μ 是权,那么算子D2Mu:B→Hμ是紧算子的充要条件是D2Mu:B→Hμ是有界算子且对于B→Hμ中在Δ的紧子集上一致收敛于0的任意有界列(fk)k∈N有
3 主要定理及证明
定理3.1 设u∈H(Δ),μ 是权,则算子D2Mu:B→Hμ是有界算子当且仅当下列两式成立


证明先假设(1),(2)成立,对于任意 f∈B,由引理2.1,2.2可得
|(D2Muf)(z)|=|(u(z)f(z))"|
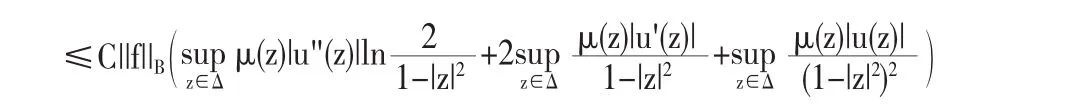
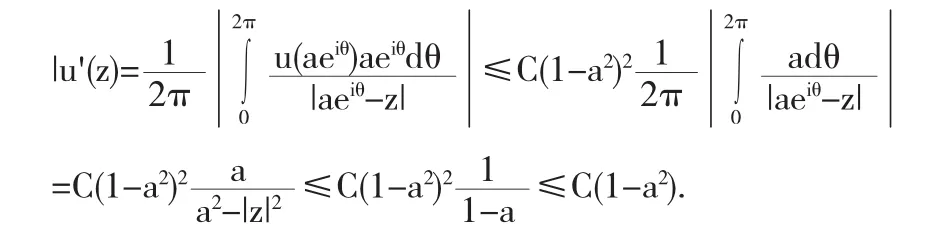
由于所以 |u'(z)|≤C(1-|z|2),所所以D2Mu:B→Hμ是有界算子.
下面假设D2Mu:B→Hμ是有界算子,那么存在一个正常数C使得对于任意f∈B,

取w∈Δ,以及检验函数

满足 fw∈B,supw∈D||fw||B≤C 且
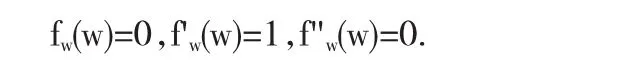
由于D2Mu:B→Hμ是有界算子,所以

取w∈Δ,以及检验函数
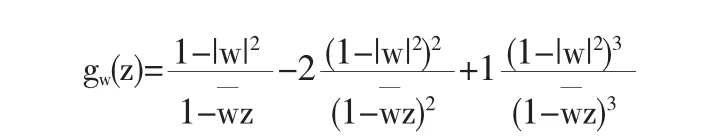
满足 gw∈B,supw∈D||gw||B≤C 且

由于D2Mu:B→Hμ是有界算子,所以
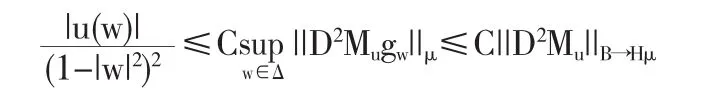
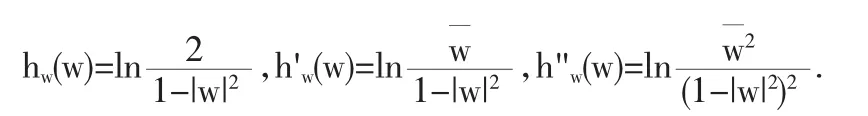
由于D2Mu:B→Hμ是有界算子,所以

定理 3.2设 μ∈H(Δ),μ 是权,则算子D2Mu:B→Hμ是紧算子当且仅当D2Mu:B→Hμ是有界算子,且下列两式成立

证明首先假设D2Mu:B→Hμ是有界算子且(3),(4)成立.
令(ki)i∈N是 B 中使得且Ki是Δ上任一紧子集上一致收敛于0的序列,由假设知∀ε>0存在一个δ∈(0,1),当 δ<|z|<1 时,

因为 D2Mu:B→Hμ是有界算子,由定理 3.1可知(1),(2)成立,由(2)成立可得因为 ki是 Δ 上的任一紧子集上一致收敛于0的序列,由柯西估计可知在Δ的任一紧子集上一致收敛于0的序列,所以∃i0∈N,使得当 i>i0时,有
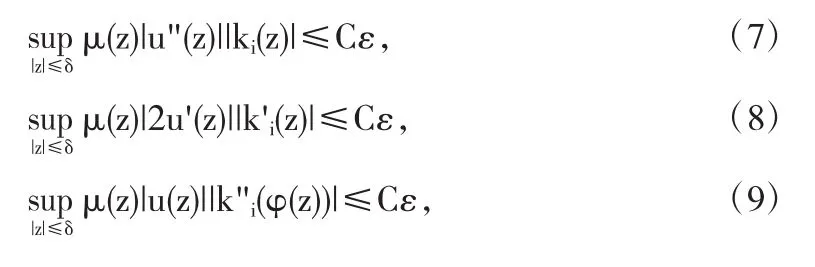
由(5)-(9)以及∀ε>0 存在一个 δ∈(0,1),当 δ<|z|<1 时,可知,当 i>i0时有所以由引理 2.3 可得 D2Mu:B→Hμ是紧算子.

相反地,假设D2Mu:B→Hμ是紧算子,显然D2Mu:B→Hμ是有界算子.令的点列.
取检验函数 fi(z)=fzi(z),那么 fi(zi)=0,f'i(zi)=1,f"i(zi)=0,fi∈且fi在Δ的任一紧子集上一致收敛于0,由引理2.2可得在上式两边令i→∞,可得成立.取检验函数,gi(z)=gzi(z),可得(4)式成立.取检验函数hi(z)=hzi(z)以及三角不等式可得(3)式成立.
〔1〕Zhao Ruhan.Composition operators from Bloch type spaces to Hardy and Besov spaces[J].Journal of Mathematics Analysis and Application,1999,233(2):749-766.
〔2〕Stevi′c S.Composition by followed by differentiation from and Bloch spaces to nth weight-type spaces on the unit disk[J].Applied Mathematics and computation,2010,216(12):3450-3458.
〔3〕于燕燕,刘永民.从混合模空间到Bloch-型空间微分算子与乘子的积[J].数学物理学报,32A(1)(2012):68-79.
〔4〕刘晓曼,于燕燕.从H∞到Zygmund空间微分算子与乘子的积[J].徐州师范大学学报(自然科学版),2011(01).
〔5〕Stevi′c S Composition by followed by differentiation from H∞and Bloch spaces to nth weight-type spaces on the unit disk [J].Applied Mathematics and computation,2010,216(12):3450-3458.
〔6〕Zhu K H,Bloch type spacesofanalyticfunctions,Rocky Mountain J.Math,1993,23(3):1143-1177.
〔7〕张超.单位球上加权Bergman-Nevanlinna空间到Bloch-型空间上乘法,复合,微分算子的乘积(英文)[J].纯粹数学与应用数学,2016,32(3):271-287.
〔8〕高超.有界解析函数空间上的算子D2Mu的有界性和紧性[J].长沙大学学报,2016,30(5):5-6.
O177.2;O174.5
A
1673-260X(2017)12-0001-02
2017-10-13
