三维空间凸透镜成像坐标定位法

刘凯伦

(山东省青岛第二中学 山东 青岛 266061)

学生创新园地

三维空间凸透镜成像坐标定位法

刘凯伦

(山东省青岛第二中学 山东 青岛 266061)

通过深入探究空间点和线段的凸透镜成像规律,概括总结创建出一新的成像方法“凸透镜成像坐标定位法”．突破解决了传统几何光学“透镜成像作图法”所无法解决的一些难题，可精确定位每一像点在坐标系中的位置以及物体凸透镜成像的形状，画出三维空间物体跨越焦平面时的立体发散图像．举例阐明了“凸透镜成像坐标定位法”的作图要点及注意事项.

凸透镜成像作图法 坐标定位法 坐标定位数据表

在几何光学的学习中，当使用“透镜成像作图法”作图时，往往会碰到两类问题无法解决：

一是，物点的两条特征光线接近平行时，无法确定像点的准确位置，图像严重变形；

二是，构成物体的某一线段接近或跨越焦平面时，无法画出它的光路图，得不到物像．

我们的目的就是要找出凸透镜成像更为有效的方法，解决上述难题．

1 建立凸透镜成像的数学模型

1.1 空间点的凸透镜成像坐标定位

首先，假设透镜为理想透镜．建立直角坐标系．

图1 没跨越焦平面线段的凸透镜成像

讨论通过S0的两条特征光线:

由通过光心光线的基本性质，得

(1)

由平行于光轴光线的基本性质，得

(2)

解之得

(3)

(4)

则可以证明，必有

(5)

结论1：对空间任一物点，其对应的凸透镜成像点由公式(3)、(4)、(5)唯一确定．

公式(3)、(4)、(5)被称为凸透镜成像坐标定位公式．

1.2 空间线段的凸透镜成像坐标定位

1.2.1 如果线段S1S2没跨越焦平面F，则其凸透镜成像必为一线段．如图1所示.

证明：在线段S1S2上任取一点S3(X3，Y3)，因S1S2，S3在一直线上，线段S1S3与线段S3S2斜率相等

代入公式(3)、(4)，整理，可得其斜率

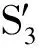
代入公式(3)、(4)，可得其斜率

因为

所以

K1=K2

由数学定理：通过同一点的两直线，如果它们斜率相等，则它们必重合．

图2 跨越焦平面线段的凸透镜成像

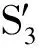
1.2.3 上述两结论，同理也可推广到空间直角坐标系．

结论2：对空间任一线段，第一，若它未跨越焦平面，其对应的凸透镜成像仍为一线段；第二，若跨越焦平面，其凸透镜成像便分裂、向两端发散，变为仍在一直线上的两射线．而且线段与焦平面交点的像，便是此直线的无穷远“端点”．

此结论被称为凸透镜成像坐标定位法则．

2 凸透镜成像坐标定位法作图

2.1 由“凸透镜成像坐标定位公式”可逐点描绘平面图形的精确成像

【例1】画出一不跨越界面F的圆的凸透镜成像图，如图3所示.

图3 不跨越焦平面F的圆的凸透镜成像图

(1)建立坐标系，定焦距f=100；圆的直径为80．

(2)用八边形来逼近此圆，设定拐点坐标．若需要更精细的部位，可多增设几个点；

(3)根据结论1公式(3)、(4)计算出对应像点的坐标．建立数据表(略)．

(4)逐点描绘出图像．

若使用“Excel”或“几何画板”等工具，则数据表和图像都可自动生成，非常方便、快捷．

2.2 由凸透镜成像坐标定位法结论2描绘跨越界面f的图形的精确成像

【例2】精确画出一跨越界面F的三角形的凸透镜成像，如图4所示.

图4 跨越焦平面的平面三角形凸透镜成像图

(1)设定f=60，a，d，g的坐标如表1所示．

表1 跨越焦平面的平面三角形凸透镜成像数据表

(2)由结论1公式(3)、(4)，计算出像点a′，d′，g′的坐标．列出数据表．

(3)由结论2第一条，因线段ag没跨越界线F，可直接连接a′，g′； 由结论2第二条，因线段ad，gd均跨越界线F，故先用虚线连接a′，d′和g′，d′，再反向向两端画延长线．即得完整图形．

2.3 结合凸透镜成像坐标定位法两个结论描绘跨越焦平面F的空间立体图形的精确成像

在空间直角坐标系O-XYZ中，置透镜于OYZ平面，光心与原点O重合、光轴与OX轴重合．

【例3】空间三棱锥凸透镜坐标定位成像(Z坐标：45°，1∶2)如图5所示.

图5 空间三棱锥凸透镜坐标定位成像图

表2 空间三棱锥凸透镜坐标定位成像数据表

从数据表可以看出C点已越过焦平面．所以在作图时，A′，B′，D′之间可直接连接． 但由结论2，所有连接像点C′的线段A′C′，B′C′，D′C′都必须向两端反向延长至无穷．

3 “凸透镜成像坐标定位法”作图要点

由上节所述，可概括总结得出坐标定位作图法的作图要点：

(1)建立坐标系，定焦距f；

(2)在坐标系左侧画出物体图形，设定拐点坐标．应避免将拐点设在焦平面F上；

(3) 根据结论1公式(3)、(4)，计算出对应像点的坐标，建立数据表；

(4) 根据结论2第一条，先画没跨越焦平面F的线段的像线，可直接连接其像点；根据结论2第二条，对跨越焦平面F的线段，应先用虚线连接其像点，再反向向两端画出延长线．即得物体完整的凸透镜成像图．

4 结论

(1) 本文简要地对“凸透镜成像坐标定位法”的创建进行了证明．重点突破传统“透镜成像作图法”存在的问题．精确确定了每一像点的位置，并画出跨焦平面物体的发散光路图．

(2) 举例阐明了“凸透镜成像坐标定位法”的作图方法、要点及注意事项．

(3) 本文所建立的“凸透镜成像坐标定位法” 可广泛应用于几何光学教学、研究，以及教学仪器的设计制作等．

(4) 此方法同样适用于其他各类透镜、反射镜等．

1 李晓彤.几何光学·像差·光学设计(第三版).杭州：浙江大学出版社，2014.2～90

2 王家伟.巧用数学法解凸透镜成像问题.中学物理,2013,31(8):89

3 刘凯伦.凸透镜成像的数学模型——凸透镜数据成像基本原理的探究.第32届青岛市科技创新成果大赛.

CoordinateLocationMethodofConvexLensImaginginThreeDimensionalSpace

Liu Kailun
(Qingdao second middle school,Shandong Qingdao,Shandong 266061)

In this paper, we deeply explore the law of convex lens imaging of spatial point and line segment, a new imaging method "convex lens imaging coordinate positioning method" is summarized. It breaks through some difficult problems that cannot be solved by traditional geometrical optics " The drawing method of lens imaging ",The position of each image point in the coordinate system and the shape of Convex lens imaging can be accurately located, Draw the solid divergence image of the three-dimensional object across the focal plane。The drawing key points and matters needing attention of "convex lens imaging coordinate positioning method" are illustrated by examples

the drawing method of convex lens imaging；coordinate positioning method；coordinate positioning data table

2017-04-12)