基于遗传算法的渡槽传感器优化布置

顾培英， 王岚岚， 邓昌， 王建

(1.南京水利科学研究院 材料结构研究所，江苏 南京210029; 2.水利部 水科学与水工程重点实验室，江苏 南京 210029)

基于遗传算法的渡槽传感器优化布置

顾培英1,2， 王岚岚1,2， 邓昌1,2， 王建1,2

(1.南京水利科学研究院 材料结构研究所，江苏 南京210029; 2.水利部 水科学与水工程重点实验室，江苏 南京 210029)

对于老旧渡槽，科学的损伤诊断有助于及时发现隐患并进行处理，其中传感器的优化布置是损伤诊断的关键。分别阐述了渡槽动力特性研究现状、传感器优化布置的方法以及基于遗传算法的桥梁传感器优化布置，最后分析了渡槽与桥梁的异同。基于遗传算法的渡槽传感器优化布置，可以借鉴遗传算法在桥梁传感器优化布置中的改性方法，综合考虑渡槽槽身底板、侧壁、支撑结构的动力特性，优化传感器的数目和布置位置。阐述和分析结果为基于遗传算法的渡槽传感器布置位置、遗传算法的改进提供参考。

渡槽;损伤诊断;传感器优化布置;遗传算法;动力特性;桥梁

渡槽是南水北调等大型水利工程中的重要建筑物，在跨流域调水过程中发挥着关键作用[1]。实际运行过程中，由于槽内水体和环境因素的影响，造成了渡槽结构不同程度的破坏[2]。渡槽产生的病害症状主要有:表层混凝土剥蚀、蜂窝、钢筋外露、各种原因的裂缝、渗漏、地基不均匀沉降、整体或局部失稳、倒塌、结构内力及变形、挠度过大以及各种材料老化等[3-5]。科学的损伤诊断及安全评价有助于发现渡槽的早期病害，从而及时维修加固，以保证渡槽的结构性能，延长渡槽的使用年限，避免发生灾难性事故[6]。

目前，结构损伤诊断技术广泛应用于航空航天、海洋工程、机械电子等领域，由于渡槽的损伤诊断是近年来遇到的新问题，所以结构的损伤诊断技术暂未在渡槽领域应用。目前，老旧渡槽不断增多，实际渡槽维护工程急需相关标准和规范及渡槽损伤诊断方面的研究成果[7]。

结构损伤诊断的各种方法中无损检测法具有准确、快捷和无破损等特点，在结构损伤诊断中具有重要意义[8]。传统的无损检测技术如超声波法、冲击回波法、声发射法、红外线法和雷达法等均属于局部损伤诊断方面的技术方法[9]，此类方法在应用时工作量大、费用高，而且难以完整、准确地评价整个结构体系。

结构动力特性只与结构本身有关，与荷载等外部条件无关，一旦损伤，必然引起动力特性的改变[10]。损伤动力诊断依据动力测试信号分析结构的固有频率、阻尼和模态振型等动力特性，进而诊断结构损伤位置和程度，最终做出准确的安全评定，因而具有全局性[11]的特点。

分析实际渡槽结构的动力特性时要依赖传感器的测量结果，所以，离不开传感器的布置。考虑到经济性和可行性，一般应尽量布置较少的传感器，故需对传感器的数目及布置位置进行优化，即传感器的优化布置[12-13]。目前，尚未见到渡槽传感器优化布置的国内外相关文献。

渡槽又称输水桥，具有和桥梁相似的受力和传力特点，所以，可以借鉴桥梁结构方面的损伤诊断方法。但渡槽槽内有大量水体，结构头重脚轻，与桥梁结构存在一定差异，因此，若根据桥梁结构的传感器布置来进行基于遗传算法的渡槽传感器优化布置，需要分析渡槽结构的动力特性，改进遗传算法，使得该算法更加适用于渡槽的结构特点，以提高运算效率和准确度，为损伤诊断和安全评价提供基础。

1 渡槽动力特性

渡槽顶部大质量的水体以及环境激励下水体的晃动将影响渡槽结构的动力特性，即流固耦合作用[14]。建立有限元模型是分析槽内水体对渡槽动力特性影响的重要方法。徐建国等[15]为了研究大型双槽渡槽的动力特性，根据Housner理论，即采用多质量块和多弹簧振子模拟槽内水体，分析渡槽空槽和设计水位2种工况下前12阶的频率和振型。结果表明：水体的存在并未改变结构的整体振动形态，有水工况比对应各阶无水工况的振动频率小。董荭、苏小凤等[16-17]采用附加质量法考虑矩形渡槽内不同水深的作用，得出相同的结论。BAI B等分析了设计水位和1/2水位时渡槽结构的动力特性，结果表明，频率随水深的增加而减小[18]。BAI X L等认为水对渡槽结构的模态形状无影响,即有水、无水工况的模态形状外观相似[19]。季日臣等[20]进一步分析了是否考虑水体晃动对渡槽振动频率的影响，指出了不考虑水体晃动、仅将水当作刚体施加于槽身时，将夸大水对渡槽自振频率的影响，同时槽内是否有水也将影响渡槽结构的振型：槽内无水时，该结构的第一阶振型为顺槽方向，第二阶振型为横槽方向;槽内有水时，第一阶振型为横槽方向，第二阶振型为顺槽方向，方向相反。马文亮等[21]认为，随着水深的增加，渡槽的自振频率减小，这是由于水的存在增加了整体结构的质量，且渡槽自振频率变化趋于平缓，因此，水体对渡槽自振频率的影响不大。张成江[22]分析了拱式渡槽无水工况和有水工况(槽内水体以水荷载的方式施加于渡槽槽身)模型提取的振型图，证明槽中水体对渡槽结构振型有较大影响：前7阶振型特征大致相同，幅度不同，出现的顺序一致，从第8到第15阶，振型的特征出现顺序发生了变化。

渡槽动力特性研究除了涉及槽内水体影响，还包括如下因素：截面形式、桩-土相互作用、槽墩高度等。张银芳等[23]针对底部加厚和不加厚两种“U”形截面渡槽结构，进行了渡槽结构的动力特性计算和对比分析。吴泽玉等[24]分析了有肋和无肋的矩形渡槽和“U”形渡槽不同预应力筋配置方式的动力特性，以此选择合适的截面形式。

渡槽的抗震计算常假设地基为刚性，进而直接将渡槽固结于地面上；而实际情况是，在地震荷载作用下，由桩和土间的相互作用引起上部结构振动。王博等[25]为了分析桩-土相互作用对渡槽的动力特性的影响，建立了同时考虑流固耦合和桩-土相互作用的桩-土-渡槽-水三维仿真力学模型。周振纲[26]、李正农等[27]分析了槽墩高度变化对渡槽结构基频的影响。

渡槽结构本身的复杂性使得其动力特性研究多借助软件模拟，但试验方法更直观，是不可或缺的研究手段。顾培英等[8，28]应用应变模态试验技术对简支渡槽模型进行结构损伤诊断研究，分析槽身裂缝损伤程度与应变模态之间的关系。

现场采集渡槽的振动响应受水流因素影响较大，有效信息易被低频水流噪声淹没，据此，张建伟等[29]提出环境激励下基于二次滤波的希尔伯特-黄变换(Hilbert-Huang Transform,HHT)模态参数辨识方法，并将该方法应用于景泰川二期3泵站输水“U”型渡槽工程中，证明了HHT模态参数辨识方法能够滤除运行环境中强噪声的干扰，准确辨识渡槽频率，且识别精度高，但并未分析该方法对结构振型识别的精确性。

渡槽动力特性多通过有限元方法进行模拟研究，采用不同方法考虑槽身与水作用的有限元模型模拟计算结果差别较大，依据模型试验结果的分析较少,对槽内水体对渡槽结构频率变化影响的研究较多，针对振型的研究较少，鲜有关于渡槽传感器优化布置的研究。渡槽动力特性受截面形式、桩-土相互作用、槽墩高度等因素的影响，现有的研究中并未得出渡槽动力特性的统一规律，难以为渡槽结构的损伤诊断提供有用的参考资料。

2 传感器优化布置

2.1 传感器优化布置方法

渡槽损伤诊断的结果很大程度依赖于传感器的优化布置[30]，目的是在考虑经济基础的条件下最大限度地采集监测信息，并通过采集到的信息分析渡槽的动力特性[13]。常用的传感器优化布置方法有：模态动能法、有效独立法、Guyan模型缩减法、模拟退火算法、遗传算法等。模态动能法[31-32]计算结果受有限元网格划分的影响；有效独立法[33]选择的测点应变能不高，易造成信息冗余；Guyan模型缩减法[34-35]能较好地保留低阶模态，但对高阶模态的计算结果误差较大。模拟退火算法[36]需要选择初始温度、退火速度等参数，这些参数随具体问题而变化，较难选择，因此不能控制搜索效率，易导致搜索时间过长。

遗传算法[37]起源于达尔文的生物进化理论，模拟自然界“适者生存”的机制。与上述算法相比具有以下特点：①自组织、自适应和自学习能力，即可根据环境变化自动发现环境特性和规律，因此，可以解决复杂的非结构化问题;②本质并行性，适合大规模并行运算;③搜索范围广，大大减少了陷入局部最优解的可能性;④求解各类问题时只需要定义目标函数，无需梯度等其他信息[38]。因此，采用遗传算法进行结构动力特性传感器优化布置相比于其他算法更具可行性。遗传算法解决问题的一般过程如图1所示，其中参数编码、初始群体的产生、适应度函数的设计、遗传操作的设计、控制参数的设定[39]是遗传算法的5要素，遗传操作包括选择、交叉、变异3个基本遗传算子。

图1 遗传算法流程图

2.2 基于遗传算法的桥梁传感器优化布置

遗传算法不依赖于问题具体的领域，具有很强的鲁棒性，广泛应用于许多学科。大批学者采用遗传算法以及改进的遗传算法进行桥梁传感器的优化布置。

缪长青等[40]在有限元分析的基础上，采用遗传算法布置了润扬大桥的振动传感器，根据大桥前30阶模态，选择基于变形能的适应度，优化振动测点布置。左云[41]用遗传算法进行了茅草街大桥的传感器优化布置。但是，传统遗传算法应用于上述桥梁结构的传感器优化布置计算时存在如下缺点：收敛速度慢，结果的可靠性不高，易陷入局部最优等。

孙晓丹等[30]以高效、准确地找到最优值为原则，改进传统遗传算法。具体操作如下：①采用有条件的2点交叉，并采用不同基因值对换位置的方式变异，使得传感器数目在交叉、变异过程中不变；②采用自适应选择变异，防止不成熟收敛，当搜索沿着较快的寻优方向发展时，采用较小变异率，当连续若干代为恒定值时，则采用较大的变异率多次变异；③适应度最大的个体直接进入下一代以保持增长的趋势。通过哈尔滨四方台大桥模型的仿真分析，证明了改进的遗传算法在搜索能力、计算效率、可靠性等方面相比传统遗传算法有较大改善，搜索能力明显优于经典的序列法。

黄民水等[42]为解决桥梁结构健康监测中的传感器优化布置问题，针对遗传算法的上述缺陷，提出如下改进：①采用二重结构编码遗传算法时，与上述采用二进制编码的遗传算法相比提高了搜索效率；②采用最优保存策略时，保证优良个体不会被交叉、变异等遗传运算破坏，并改进了最差个体，提高了种群整体素质，有效保证了算法的收敛性；③采用部分匹配交叉的方法时，避免了由于交叉操作使得二重编码的上行附加码重复；④采用逆位变异时，确保新产生个体均为可行解；⑤采用自适应的交叉和变异方法时，在保持群体多样性的同时，又保证了遗传算法的收敛性。单德山等[43]选用不同的适应度函数采用相似的方法解决了大跨度铁路桥梁健康监测中的传感器优化布置问题。刘来君等[12]采用与文献[24]相似的方法处理了连续刚构桥的传感器优化布置问题，将部分匹配交叉改为多段交叉，随着交叉段数的增加，模态置信度矩阵的最大非对角元呈下降的趋势，从而防止传统遗传算法收敛过早、陷入局部最优解等现象，能更好地利用初始种群的多样性。

广义遗传算法[44]、混合遗传算法[45]、嵌套层迭遗传算法[46]等应用于桥梁结构传感器的优化布置时，均能改进传统遗传算法优化时的缺陷，提高运算效率。

基于遗传算法的桥梁结构的传感器优化布置时，为了提高收敛速度，增强可靠性，避免产生局部最优解，进行了相关调整，改进主要体现在以下几个方面：编码方式、适应度函数、遗传操作、保存策略、和其他算法相结合等。

3 基于遗传算法的渡槽传感器优化布置

渡槽结构从功能角度可以称为输水桥，是跨越山川、河谷、道路的架空输水建筑物，具有与桥梁结构相似的受力、传力特点[47-48]。桥梁传感器优化布置研究已较成熟，基于各种改进遗传算法的传感器优化布置也在桥梁结构中得到了很好的应用，对传感器在渡槽结构中的优化布置具有借鉴意义。

进行传感器优化布置研究的桥梁单跨跨度一般大于50 m，而渡槽的单跨跨度较小，一般小于50 m，支撑结构高度相对较高，如南水北调某渡槽单跨长40 m、墩高9.50～9.66 m[49]；双洎河大型渡槽的一个典型跨，单跨长40 m、槽墩高度18 m[50]。

渡槽动力特性的传感器优化布置研究选择梁式渡槽模型，主要是由于梁式渡槽结构简单，施工和吊装方便，应用最多[51]；但梁式渡槽的槽身具有承重作用，所以自重较重，跨中弯矩也比较大。这些原因导致了梁式渡槽的跨度较小，适用跨度一般为20 m以内，即使使用预应力技术，跨度仍局限在50 m内[52]。图2为某简支梁桥的动力特性振型图[53]，其中该段桥跨度为11.5 m。图3为简支梁式渡槽某跨的动力特性振型图[54]，其中该渡槽跨长12 m，基础底部到槽顶高18.5 m，槽内为设计水位。

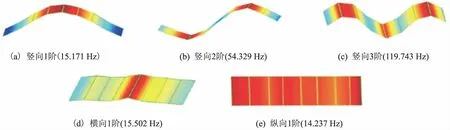
图2 简支梁桥某跨的动力特性振型图

图3 简支梁式渡槽某跨的动力特性振型图

对比分析图2和图3中的振型图得出如下结论：在跨度相差不大的前提下，简支梁桥的振型较简支梁式渡槽的振型简单，渡槽侧壁易产生变形；渡槽中的排架结构在已列出的前5阶振型中均易产生较大变形。

渡槽和桥梁结构相比有很大的区别[55]。渡槽中水体的重量相当或甚至超过结构重量[47]，环境激励下，水体会产生较大的晃动甚至飞溅；而渡槽槽壁相应较薄，在外载和水体晃动的双重作用下，易产生较大变形[56]，动力特性远比桥梁复杂[57]。渡槽结构设计裂缝控制等级高，考虑到渡槽结构长期处于水环境中，防蚀、防渗、防漏是渡槽设计研究的突出问题[58]，传感器布置既要考虑损伤对整体结构的影响，又必须易于判断局部损伤的程度。基于遗传算法的桥梁传感器布设位置大多只考虑桥面，少有将桥面和支撑结构作为整体来分析桥梁结构的动力特性，进而在结构中布置传感器的。

因此，基于遗传算法的渡槽传感器优化布置可以借鉴遗传算法在桥梁传感器优化布置中的改进方法，但布置位置需要结合渡槽本身的动力特性，不能仅布置在槽身底板处，还需要考虑槽壁和支撑结构的动力特性、槽内水体的作用等情况。

4 结语

渡槽动力特性受槽内水体的影响显著，基于遗传算法的渡槽传感器优化布置必须考虑不同水深的作用，使得传感器布设在不改变位置、经济允许的条件下，准确分析出不同工况下渡槽的动力特性，为其损伤诊断提供依据。

采用模型试验和数值仿真计算相结合的方式进行综合研究，以提高传感器优化布置结果的可靠性。

桥梁传感器多布置在桥面，考虑到渡槽与桥梁的差异及动力特性的不同，渡槽传感器优化布置时应综合考虑槽身底板、侧壁、支撑结构的动力特性，通过改进遗传算法的编码、适应度函数、遗传操作、最优保存策略等，提高渡槽传感器优化布置的运行效率，避免陷入局部最优解。

[1] 陈厚群．南水北调工程抗震安全性问题[J]．中国水利水电科学研究院学报，2003，1(1)：17-22．

[2] 陈武,刘德仁,董元宏，等．寒区封闭引水渡槽中水温变化预测分析[J]．农业工程学报，2012，28(4)：69-75．

[3] 单旭辉．放水河渡槽混凝土冻胀裂缝处理技术[J]．南水北调与水利科技，2010，8(1)：133-135．

[4] ZHENG C,PENG H,LIU S,et al.Application research on the temperature control and crack prevention of the large-scale aqueduct in China's South-to-North Water Diversion Project[J].Yellow River,2012,28:635-639.

[5] 许晓会,刘斌．黑河引水工程沣峪渡槽混凝土结构病害治理[J]．水利与建筑工程学报，2010，8(5)：63-65．

[6] 王鹏．模态识别在渡槽结构损伤检测中的应用研究[D]．保定：河北农业大学，2005：3-7．

[7] 张锋．宁夏引黄灌区输水渡槽安全鉴定与评价研究[J]．人民黄河，2016，38(7)：134-137,145．

[8] 顾培英．基于应变模态技术的结构损伤诊断直接指标法研究[D]．南京：河海大学，2006：13-15．

[9] 王志坚,韩西,钟厉，等．基于结构动力参数的土木工程结构损伤识别方法[J]．重庆建筑大学学报，2003，25(4)：128-132．

[10] 吴泽玉,王东炜．基于特征参量控制的渡槽预应力张拉顺序研究[J]．长江科学院院报，2015，32(12)：125-128．

[11] 吕泳．碳纤维智能束的功能特性及其应用研究[D]．武汉：武汉理工大学，2011：18-23．

[12] 刘来君,倪富陶,孙维刚，等．多段交叉遗传算法在连续刚构桥测点优化中的应用[J]．重庆交通大学学报(自然科学版)，2016，35(2)：6-8,88．

[13] 徐峰,孟光,彭海阔，等．沉管隧道健康监测试验中传感器位置的优选[J]．振动与冲击，2008，27(2)：87-90．

[14] 丁晓唐,周逸仁,颜云燕．高阻尼橡胶隔震渡槽的设计和动力性能研究[J]．水资源与水工程学报，2013，24(1)：119-122,126．

[15] 徐建国,张威,王博，等．南水北调双槽渡槽结构动力特性有限元分析[J]．水电能源科学，2011，29(3)：74-76．

[16] 董荭,魏克伦,宋春草．大型预应力梁式渡槽动力特性分析[J]．华北水利水电大学学报(自然科学版)，2014，35(3)：32-35．

[17] 苏小凤．考虑水体质量双槽式渡槽结构地震反应研究[D]．兰州：兰州交通大学，2014．

[18] BAI B,LI Y H,DENG X S. Dynamic characteristics analysis of a large aqueduct[J].Advanced Materials Research,2011,255-260:1130-1133.

[19] BAI X L,SU H L,PAN Q.Influence of supports and water depths on dynamic characteristics of aqueduct structure[J].Advanced Materials Research,2011,243-249:4592-4595.

[20] 季日臣,许涛,苏小凤，等．考虑水体晃动的多槽式渡槽结构地震反应研究[J]．中国安全科学学报，2012(10)：94-100．

[21] 马文亮,张建华,白新理．大型预应力矩形薄壁梁式渡槽静动力分析[J]．人民黄河，2012，34(8)：122-124．

[22] 张成江．大跨度钢筋混凝土拱式渡槽动力特性及地震响应分析[D]．重庆：重庆交通大学，2015：4-25．

[23] 张银芳,乔俊蕾,白新理．基于势流理论的渡槽结构动力特性对比分析[J]．华北水利水电大学学报(自然科学版)，2014，35(2)：51-55．

[24] 吴泽玉,王东炜．预应力效应对渡槽动力特性影响分析[J]．人民黄河，2012，34(10)：131-133．

[25] 王博,申金虎,徐建国．桩-土-渡槽-水相互作用动力特性分析[J]．水电能源科学，2012(11)：101-103．

[26] 周振纲．桩-土-渡槽结构相互作用的拟动力试验及计算研究[D]．长沙：湖南大学，2014：142-151．

[27] 李正农,周振纲,朱旭鹏．槽墩高度对渡槽结构水平地震响应的影响[J]．地震工程与工程振动，2013，33(3)：245-257．

[28] 顾培英,陈厚群,李同春，等．应变模态试验技术在渡槽结构损伤诊断中的应用[J]．河海大学学报(自然科学版)，2006，34(4)：422-425．

[29] 张建伟,江琦,曹克磊，等．基于二次滤波的HHT渡槽模态参数辨识方法[J]．农业工程学报，2015(15)：65-71．

[30] 孙晓丹,李宏伟,欧进萍．大型桥梁动力检测测点优化的改进遗传算法及其应用[J]．西安建筑科技大学学报(自然科学版)，2006，38(5)：624-628．

[31] UDWADIA F E.Methodology for optimum sensor locations for parameter-identification in dynamic-systems[J].Journal of Engineering Mechanics-ASCE,1994,120(2):368-390.

[32] KAMMER D C.Sensor placement for on-orbit modal identification and correlation of large space structures[J].Journal of Guidance Control & Dynamics,1991,14(2):251-259.

[33] GAWRONSKI W,LIM K B.Balanced actuator and sensor placement for flexible structures[J].International Journal of Control,1996,65(1):131-145.

[34] 顾荣荣,童忠钫,程耀东．挠性结构主动减振中传感器和激振器的优化布置[J]．振动与冲击，1995(3)：12-18．

[35] CHEN S T,FAN Y H,LEE A C.Effective active damping design for suppression of vibration in flexible systems via dislocated sensor actuator positioning[J].JSME International Journal Series C-Dynamics Control Robotics Design and Manufacturing,1994,37(2):252-259.

[36] KIRKPATRICK S,JR G C,VECCHI M P.Optimization by simulated annealing[J].Science,1983,220(4598):671.

[37] HOLLAND J.Adaptation in natural and artificial systems:an introductory analysis with applications to biology,control and artificial intelligence[J].Quarterly Review of Biology,1975,6(2):126-137.

[38] 朱宏平,余璟,张俊兵．结构损伤动力检测与健康监测研究现状与展望[J]．工程力学，2011,28(2)：1-11．

[39] 王卫争．高层建筑结构地震反应观测台阵优化布设方法研究[D]．大连：大连理工大学，2007：32-37．

[40] 缪长青,李爱群,韩晓林，等．润扬大桥结构健康监测策略[J]．东南大学学报(自然科学版)，2005，35(5)：780-785．

[41] 左云．茅草街大桥健康监测方案以及传感器优化布置的研究[D]．长沙：湖南大学，2005：48-52．

[42] 黄民水,朱宏平,李炜明．基于改进遗传算法的桥梁结构传感器优化布置[J]．振动与冲击，2008，27(3)：82-86．

[43] 单德山,王振华,李乔．大跨度铁路钢桁斜拉桥传感器优化布置[J]．土木建筑与环境工程，2011，33(增刊1)：156-160．

[44] 李戈,秦权,董聪．用遗传算法选择悬索桥监测系统中传感器的最优布点[J]．工程力学，2000，17(1)：25．

[45] 马广,黄方林,王学敏．基于混合遗传算法的桥梁监测传感器优化布置[J]．振动工程学报，2008，21(2)：191-196．

[46] 张倍阳,张谢东,陈卫东，等．基于嵌套层迭遗传算法的大跨桥梁传感器优化布置[J]．武汉理工大学学报(交通科学与工程版)，2016，40(4)：745-749．

[47] 季日臣,夏修身,陈尧隆．水体晃荡作用对渡槽横向抗震影响的研究[J]．水力发电学报，2007，26(6)：30-34．

[48] 杨立信．国外调水工程[M]．北京：中国水利水电出版社，2003：10-14．

[49] 杨世浩,李正农,宋一乐，等．大型渡槽支座隔震研究[J]．振动工程学报，2009，22(2)：188-192．

[50] 彭云枫．渡槽抗震与抗风研究[D]．武汉：武汉大学，2005：36-44．

[51] 赵文华．渡槽[M]．北京：水利电力出版社，1989：21-23．

[52] 傅志敏．斜拉式大型渡槽槽身优化设计研究[D]．南京：河海大学，2003．

[53] 褚福鹏．基于动力特性试验的某简支梁桥有限元模型修正[J]．公路与汽运，2014(3)：168-170, 171．

[54] 张建伟,曹克磊,赵瑜，等．基于流固耦合模型的U型渡槽模态分析及验证[J]．农业工程学报，2016，32(18)：98-104．

[55] 季日臣,苏小凤,严娟．水体质量对大型梁式渡槽横向抗震性能影响研究[J]．地震工程学报，2013，35(3)：569-574．

[56] 赵堃,王春青,张旸，等．基于ADINA的重力坝流固耦合动力特性分析[J]．科学技术与工程，2012，12(32)：8788-8792．

[57] 刘云贺,陈厚群．大型渡槽铅销橡胶支座减震机理的数值模拟[J]．水利学报，2003(12)：98-103．

[58] 刘东常,吴长征，岳中明，等．大型预应力混凝土梁式渡槽结构分析及设计研究[J]．华北水利水电学院学报，1999,20(4)：16-20．

OptimalArrangementofAqueductSensorBasedonGeneticAlgorithm

GU Peiying1,2， WANG Lanlan1,2， DENG Chang1,2， WANG Jian1,2

(1.Materials and Structural Engineering Department, Nanjing Hydraulic Research Institute, Nanjing 210029, China;2.Key Laboratory of Water Science and Engineering, Ministry of Water Resources, Nanjing 210029, China)

In recent years, the old aqueducts have been increasing, and the scientific damage diagnosis can help to find out the hidden trouble and to deal with them.The optimal arrangement of sensors is critical for damage diagnosis.At present, there are many literatures about optimal arrangement of bridge sensors, but there are not any relevant literatures on optimal placement of aqueduct sensors based on genetic algorithm.In order to fill in the blank, we expound the current situation of the research on the dynamic characteristics of aqueduct, the methods of optimal placement of sensors and the optimal arrangement of bridge sensors based on genetic algorithm. Finally, we analyze the similarities and differences among all the characteristics ofaqueduct and bridge, the analytical results will provide a reference for the placement of aqueduct sensors and the improvement of genetic algorithm.

aqueduct; damage diagnosis; optimal arrangement of sensor; genetic algorithm; dynamic characteristics; bridge

杜明侠)

TV312

A

1002-5634(2017)06-0054-06

2017-04-24

国家重点研发计划课题(2016YFC0401807)；中央级公益性科研院所基本科研业务费专项资金项目(Y417012)。

顾培英(1968—),女,江苏如东人,教授级高级工程师,博士,从事结构健康诊断和安全评估方面的研究。wglaln@sina.com。

王岚岚(1993—),女,江苏连云港人,硕士研究生,从事结构健康诊断方面的研究。E-mail:1774853053@qq.com。

10.3969/j.issn.1002-5634.2017.06.008