预应力高强混凝土波形板桩正截面抗弯承载力的计算模型及分析
2018-01-02胡少伟黄逸群范向前
胡少伟, 黄逸群, 范向前
(1.南京水利科学研究院 材料结构研究所,江苏 南京 210029; 2.河海大学 力学与材料学院,江苏 南京 211100)
预应力高强混凝土波形板桩正截面抗弯承载力的计算模型及分析
胡少伟1,2, 黄逸群1,2, 范向前1
(1.南京水利科学研究院 材料结构研究所,江苏 南京 210029; 2.河海大学 力学与材料学院,江苏 南京 211100)
预应力高强混凝土波形板桩作为一种新型的基坑、边坡支护结构,由于其具有挡土面积大、外观优美等特点,具有很好的工程应用前景。其抗弯承载力及对应变形情况是设计的关键,为了研究波形板桩的抗弯承载力学性能,基于截面等效假定,建立了预应力混凝土波形板桩正截面抗弯承载力的计算模型,得到了中性轴高度、截面弯矩、截面曲率表达式以及挠度的计算方法。为了验证计算模型的合理性,采用有限元单元法对抗弯试验情况进行了模拟,计算结果、试验结果和模拟结果整体吻合良好,3种结果中的抗裂弯矩值、极限弯矩值的误差基本在5%以内。
预应力;混凝土;波形板桩;抗弯承载力;弯矩-挠度曲线
预制混凝土桩作为新型的支护结构正被广泛地用于基坑、边坡、路基等支护工程中。目前,较为常见的预制混凝土桩主要有预应力混凝土管桩、预应力混凝土矩形桩及预应力混凝土空心方桩,且对于这些混凝土桩的应用与研究相对成熟。王广宇[1]针对预应力混凝土空心方桩的生产工艺、设计计算、工程应用及产品标准等方面进行了系列研究,总结了一整套生产工艺技术,并提出了简易的设计计算方法;LIU Hanlong等[2]对现浇混凝土大直径管桩在软土地基中进行路基处理展开了研究,通过对管桩施加荷载,分析了不同土层中管桩的力学响应,提出了一种PCC管桩的新使用方法;俞峰等[3]考虑了混凝土开口管桩的土塞效应和挤土效应,建立了开口管桩的设计模型,通过分析比较得出桩基规范[4]提出的预制桩建议值偏保守,使得经验计算承载力值很可能小于实际值;XING Haofeng等[5]对长预应力高强混凝土管桩打桩时的性能及对桩周围土壤的影响进行了研究,发现轴力沿桩身呈非线性分布,且非线性程度与施加荷载的大小呈正相关; ZHOU Mi[6]等针对现浇混凝土大直径管桩在打入软土的过程中桩尖几何形态对桩管内外土壤流动的影响,进行了大变形有限元分析,得出具有45°尖端角的锥形尖端角为最佳几何尖端角;董金玉等[7]采用自平衡试验法进行桩基的静载试验,并结合有限元模拟技术对桩体的力学特性进行了研究。上述预制混凝土桩的研究及应用较为成熟,且在国内已有相关配套标准及规程[4,8-9]。
预应力高强混凝土波形板桩,简称波形板桩,作为新型的支护结构近几年从国外引进,因其具有挡土面积大、外观优美、性价比高等特点在基坑支护工程中具有很好的应用前景,但目前仅有少量针对这种波形板桩[10-11]力学性能的研究,因此有必要对波形板桩的力学性能开展相关研究。波形板桩的抗弯性能是其重要的力学性能之一,本文针对波形板桩的抗弯性能,对波形板桩在四点弯加载全过程中的正截面抗弯承载力及相应的力学响应进行了分析研究。
1 预应力混凝土波形板桩正截面抗弯承载力计算模型的建立及分析
1.1 波形板桩抗弯加载过程计算模型
1.1.1 截面等效假定
波形板桩截面形式如图1所示,其形状近似为“U”型,若完全根据其截面形状进行计算,则计算过程十分复杂,若从截面抗弯受力的角度分析[11],其受力特点与“工”型截面相近,故在计算时可将“U”型截面等效为“工”型截面,截面等效计算模型如图2所示。

图1 波形板桩截面形式
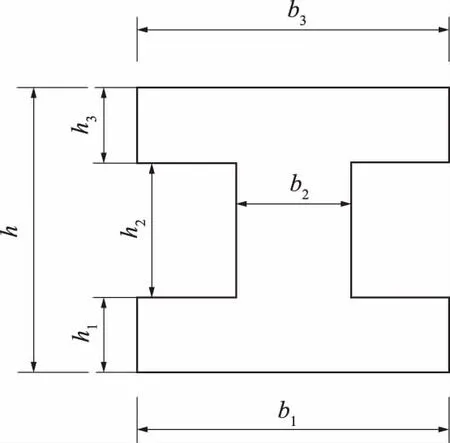
图2 “工”型截面形式
截面等效换算的原则是:等高度、等面积、等刚度。根据上述原则,两种截面在换算中有如下关系:
(1)
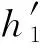
1.1.2 混凝土应变及应力关系表达式
假定波形板桩截面出现裂缝后该截面内应变分布仍为线性,且在中性轴位置应变为零,截面在未裂处满足线弹性应力-应变关系,截面的应变分布及应力分布如图3所示。根据混凝土抗拉应力-应变特征[12],其应力值在达到峰值后会出现相当大程度的应力跌落,出于简化考虑,假定混凝土在达到极限抗拉应变后即开裂,且在裂缝段截面应力为零。

图3 波形板桩混凝土截面沿高度方向应力和应变分布
同时,由于在板桩结构达到失稳破坏状态时,前桩身变形量相较于其整体尺寸较小,可基本认为其变形为小变形,则埋于板桩内的预应力钢棒(钢筋)与板桩混凝土部分不会出现太大滑移,故假定钢棒(钢筋)应变量与混凝土应变一致。
波形板桩在受弯加载过程中底部混凝土达到抗拉极限而出现裂缝,截面应力分布出现变化,中性轴也随之移动,根据上述截面应变线性分布的假定,以截面底部中心为坐标轴原点,则任意受力时刻的截面上任意高度的应变表达式如下:

(2)
式中:y为截面上任意一点的高度值;ε(y)为截面上任意高度位置的应变值;εt为截面底部的应变值;y0为中性轴的高度值。
由于波形板桩在受弯加载之前在截面上施加了预应力,则在受弯加载时,混凝土的极限抗拉强度有所提高,其极限拉应变也随之提高,提高后的极限拉应变表达式为:
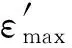
(3)

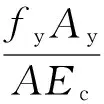
(4)
式中:fy为预应力钢棒单位面积所产生的预应力值;Ay为截面内预应力钢棒的总面积;A为混凝土截面面积;Ec为混凝土弹性模量。
根据上述截面应力分布假定,同时由于截面施加了预应力,混凝土的本构关系出现了相对偏移,如图4所示。
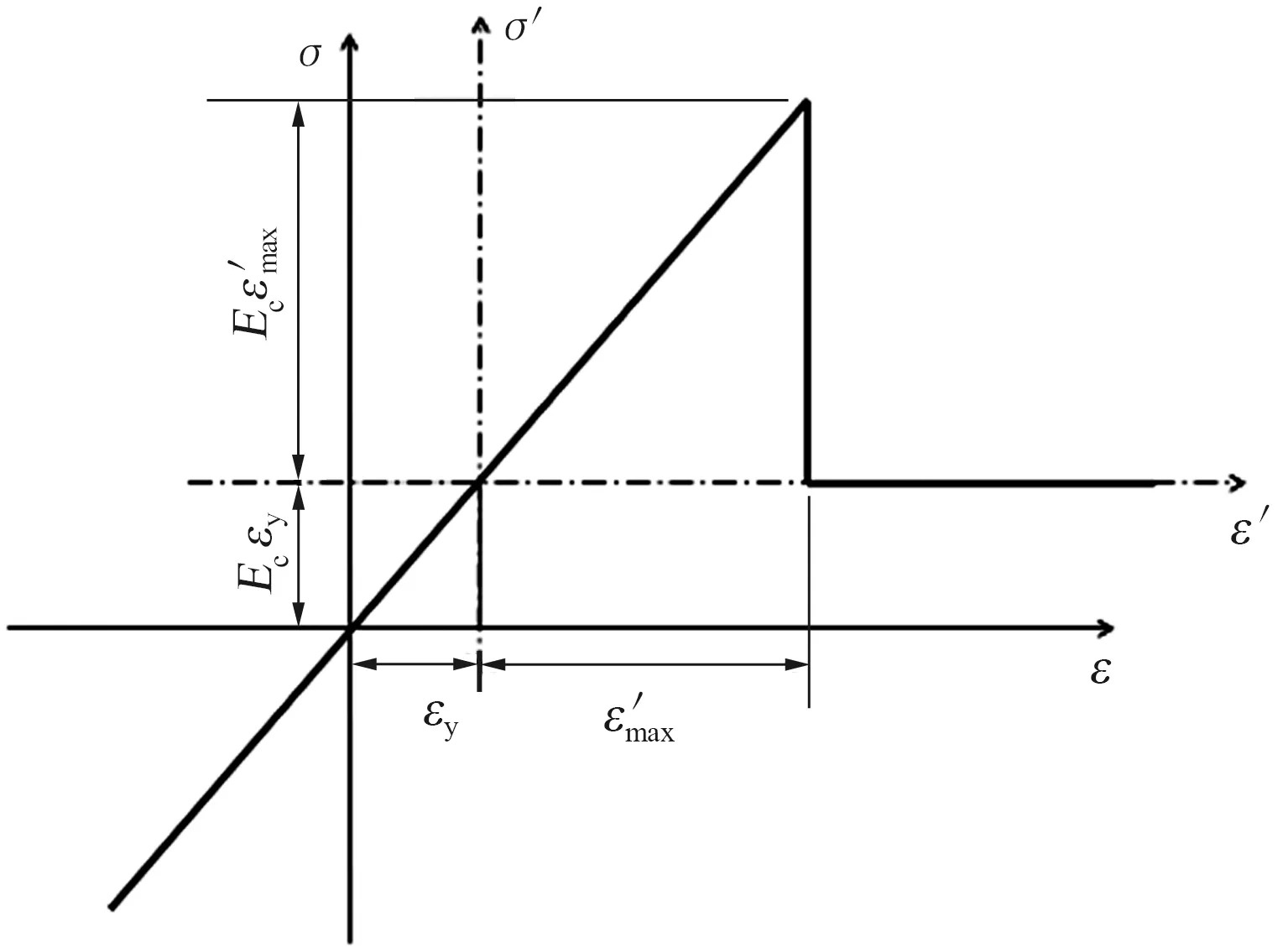
图4 应力-应变关系在预应力施加后的相对偏移
当混凝土失效时,其应力值降至一相对值,则在任意受力时刻,截面上任意高度的应力表达式为:
(5)
1.1.3 截面中性轴的确定及弯矩的表达式
由于板桩受弯时,正截面方向上合力为零,结合上述表达式,则有如下等式:

(6)
式中:F为正截面上的合力;b(y)为高度值为y处的截面宽度;Ey为预应力钢棒弹性模量;yi为第i根预应力钢棒的高度值;As为单根预应力钢棒的截面面积。
已知板桩底部应变εt,且假定在高度yf处,有:

(7)
式(6)可展开为:

(8)
由于yf可用y0表示,则上式是一个关于y0的一元方程,通过求解该方程,则可以得出中性轴的高度y0。对于“工”型截面来说,y0的解析表达式十分复杂,且为分段表达式,故求解时可以考虑采用数值方法直接求解。
在求得截面中性轴高度y0后,根据弯矩的定义,截面的弯矩M可由下式求得:

∑Eyε(yi)As(y0-yi)。
(9)
式中:i=1,2,…,n;n为预应力钢筋根数。
1.1.4 截面曲率及跨间挠度的计算
根据截面曲率的定义,截面曲率κ的表达式为:

(10)
令式(10)中y=0,根据上述坐标轴的定义,此时混凝土底部应变ε(0)即为εt,则截面曲率可简化为:

(11)
由于波形板桩在受弯时沿径向各个截面处所受弯矩不同,中性轴高度及底部应变也不相同,所以上式应该是关于板桩在径向上的坐标x的函数,即:
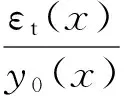
(12)
式中:κ(x)为径向x截面处的曲率;εt(x)为径向x截面处的底部应变;y0(x)为径向x截面处的中性轴高度。
对曲率κ(x)进行二次积分,则挠度函数ω(x)可表示为:
ω(x)=∬κ(x)dx+c1·x+c2。
(13)
式中c1、c2由波形板桩的边界条件确定。
1.1.5 波形板桩的正截面受弯加载计算步骤
由于预应力混凝土波形板桩在受弯加载过程中底部应变随着施加荷载的增加而单调递增,故选取截面底部应变εt为自变量,经过整理,该波形板桩加载过程计算步骤如下:
步骤1指定预应力混凝土波形板桩截面底部应变值εt(由于受拉,为非负值)。
步骤2由式(7)及式(8)联立求解得到该波形板桩截面的中性轴高度y0。
步骤3由式(9)求得桩截面对应的弯矩M,并由式(11)求得桩截面曲率κ。
步骤4对桩截面底部应变值εt增加一个步长量Δε,并重复上述步骤,如此循环若干次,得到κ-M及y0-M关系曲线。
步骤5根据预应力混凝土波形板桩在不同受弯条件的弯矩分布,求得M-x关系曲线,并根据步骤4得到的κ-M关系曲线,联立求得κ-x关系曲线。
步骤6根据κ-x关系曲线,拟合得到曲率函数κ(x),将其代入式(13)得出波形板桩挠度曲线。
1.2 预应力混凝土波形板桩四点弯加载过程的力学响应计算
以A型预应力混凝土波形板桩为例[13],采用上节推导得到的计算模型,对该类型波形板桩的四点弯加载进行了计算并分析其力学响应特性。该波形板桩的截面如图5所示,板桩长度为6 m,支座间跨度为4 m,该波形板桩的四点弯加载布置如图6所示。
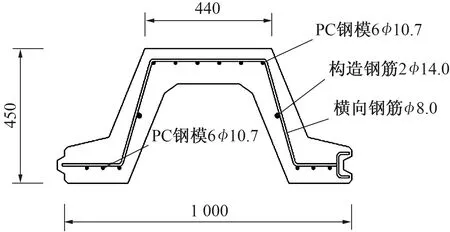
图5 A型预应力混凝土波形板桩截面示意图(单位:mm)

1—加载点;2—支座
计算选取的基本尺寸参数如下:b1为0.45 m;b2为0.26 m;b3为0.44 m;h1为0.14 m;h2为0.19 m;h3为0.12 m。计算采用的基本材料的参数见表1。

表1 基本材料的计算参数
1.2.1A型预应力混凝土波形板桩弯矩-挠度关系
计算所得的加载过程中纯弯段弯矩-挠度曲线如图7所示。
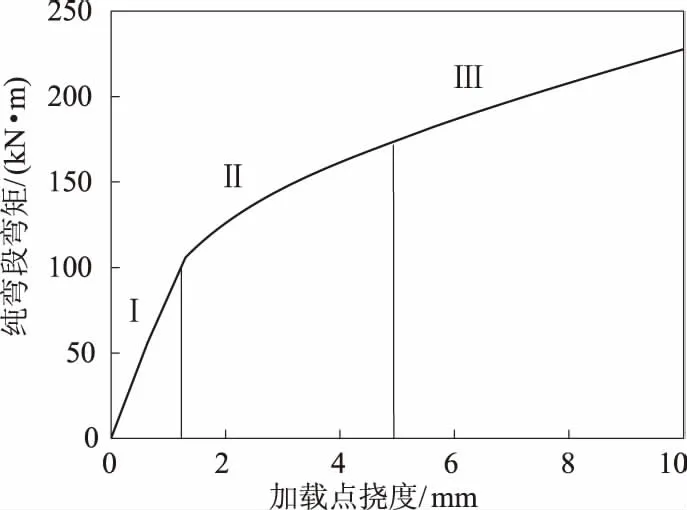
图7 计算得的纯弯段弯矩-加载点挠度曲线
在A型预应力混凝土波形板桩失稳破坏之前,根据曲线斜率的变化情况,加载阶段被分为3个阶段:在加载初期即Ⅰ阶段,截面具有较大的抗弯刚度,且力学响应表现为线弹性,随着荷载的增大,预应力在混凝土受拉区的作用逐渐被抵消;当加载弯矩达到截面抗弯弯矩时,加载进入Ⅱ阶段,底部混凝土开裂且退出受拉工作状态,预应力钢棒开始逐渐承担截面抗弯所需的拉应力,弯矩-挠度曲线斜率的变化率较大,本阶段为结构抗弯性能从弹性转向塑性的调整阶段;进入Ⅲ阶段后,弯矩-挠度曲线的斜率基本为一稳定值,此时结构完全进入塑性阶段,底部混凝土基本退出受拉工作状态,底部受拉工作基本由钢棒承担。
各纯弯段弯矩值所对应的跨间挠度(即图6中两支座间的挠度分布)如图8所示。
第二次测试:用户在8901下面进行激活,同时激活在 SGSN1上,由 8901->8902进行 TAU测试,用户业务中断,看到的现象为:在源MME向目标MME发送relocation req后,等待10s,没有收到response消息,之后又重新发起hand over流程,与此同时SGSN上有对应SGSN1和SGN5之间的gtpc断链告警。
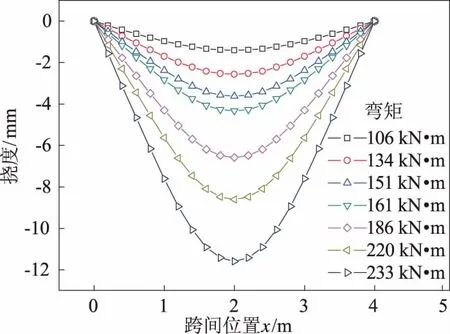
图8 计算所得的不同纯弯段弯矩下跨间挠度分布
图8中,在荷载持续施加的条件下,纯弯段挠度的变化幅度比纯弯段外区域的挠度变化幅值更明显,这是由于纯弯段内的混凝土开裂导致的。
1.2.2 截面中性轴高度与截面弯矩的关系
计算得到的截面中性轴高度-截面弯矩曲线如图9所示。

图9 计算所得的加载过程中预应力混凝土波形板桩中性轴高度-纯弯段弯矩曲线
由图9知,中性轴高度的变化特征同样可分为3个阶段:在Ⅰ阶段,截面中性轴高度基本不随截面的弯矩增大而变化,表明此时整个截面基本处于线弹性状态,且底部裂缝开展程度较轻,尚未对截面抗弯性能造成影响;进入Ⅱ阶段,在较小的一个截面弯矩变化范围内,截面中性轴高度随弯矩的增大急剧上升,这意味着底部混凝土裂缝在这一阶段扩展较快,底部混凝土逐渐退出工作状态,转由预应力钢棒代替其承载;到达Ⅲ阶段,截面中性轴高度的变化率逐渐放缓至几乎不变,这表明在经历了Ⅱ阶段的截面内部受力调整,截面底部抗拉力基本由预应力钢棒承担,截面的受力状态由原来的线弹性完全转变为塑性。
在不同的纯弯段弯矩下,跨间中性轴(即图6中两支座间的中性轴)高度分布如图10所示。
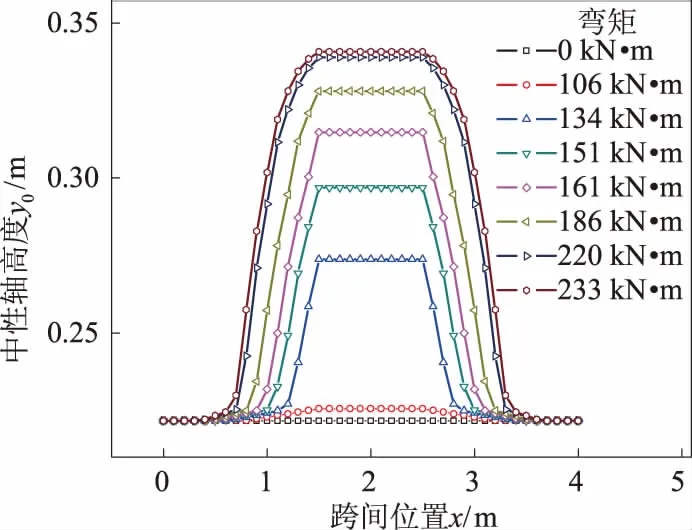
图10 计算所得的不同纯弯段弯矩下跨间预应力混凝土波形板桩中性轴高度分布曲线
由图10知,在加载初期,中性轴高度沿跨间分布情况较为平稳,总体变化不大;在加载中期,中性轴高度沿跨间分布相较于前期更为明显地呈现出中间高、两端低的分布规律,且其随纯弯段弯矩的增大而产生较大变化;进入加载末期,中性轴高度分布曲线随弯矩的增大继续上升,但上升幅度逐渐放缓,直至基本不变。
1.2.3 不同截面预压应力对波形板桩抗弯性能的影响
以上述的A型波形板桩为例,改变预应力钢棒的截面面积,得到的板桩纯弯段弯矩-挠度曲线如图11所示。

图11 计算所得的不同预应力钢棒直径下的纯弯段弯矩-加载点挠度曲线
图11中:在钢棒截面预应力不改变的情况下,板桩截面的预压应力正比于预应力钢棒的截面面积,随着截面预压应力的增大,板桩从弹性阶段进入塑性阶段所需的弯矩值随之增大,即板桩的抗裂弯矩得到了提高;同时发现,各曲线中板桩弹性阶段及塑性阶段的柔度基本不变。这说明波形板桩在失稳破坏前,截面的预应力大小只对其弹性阶段的最大弯矩(抗裂弯矩)以及破坏弯矩有影响,而对其弹性阶段和塑性阶段的柔度基本不产生影响。
2 有限元模拟基本情况及结果分析
预应力混凝土波形板桩在受力上主要由混凝土和预应力钢棒共同承担,故建模时应着重考虑混凝土与预应力钢棒,根据该波形板桩的基本设计参数(见表2),其有限元模型如图12所示,其中,预应力钢棒以埋入的方式置于混凝土模型中。

表2 预应力混凝土波形板桩的基本设计参数
运用先张法将预应力钢棒埋于混凝土中并施加预应力,为了模拟这一过程,对预应力钢棒采用降温法以模拟其预应力的施加情况。降温法温度变化量的计算公式为:

(14)
式中:ΔT为模拟时对预应力钢棒施加的温度变化量;fy为预应力钢棒上的预应力值;Ey为预应力钢棒的弹性模量;α为线膨胀系数(自由定义)。
预应力混凝土波形板桩计算采用的参数见表3,加载的边界条件如图13所示。

图12 波形板桩的有限元模型

材料密度/(kg·m-3)弹性模量/GPa抗拉强度/MPa抗压强度/MPa预应力/MPa线膨胀系数α混凝土2450362.0427.5——预应力钢棒78002001420—6941e-5

图13 模拟采用的边界条件示意图
图13中,左侧采用铰支座约束,右侧采用滑移支座约束,且在上部将两段加载线段的位移耦合于模型外部的一参考点,加载时采用对参考点施加位移条件的方式进行加载。
以A型预应力混凝土波形板桩为例,模拟得到的正截面应力及塑性应变云图分别如图14和图15所示。
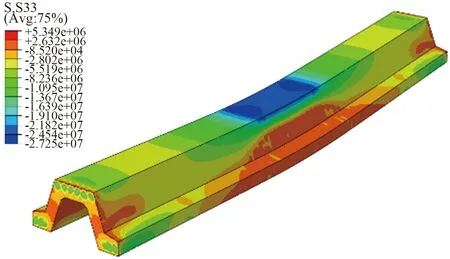
图14 预应力混凝土波形板桩的正截面应力云图
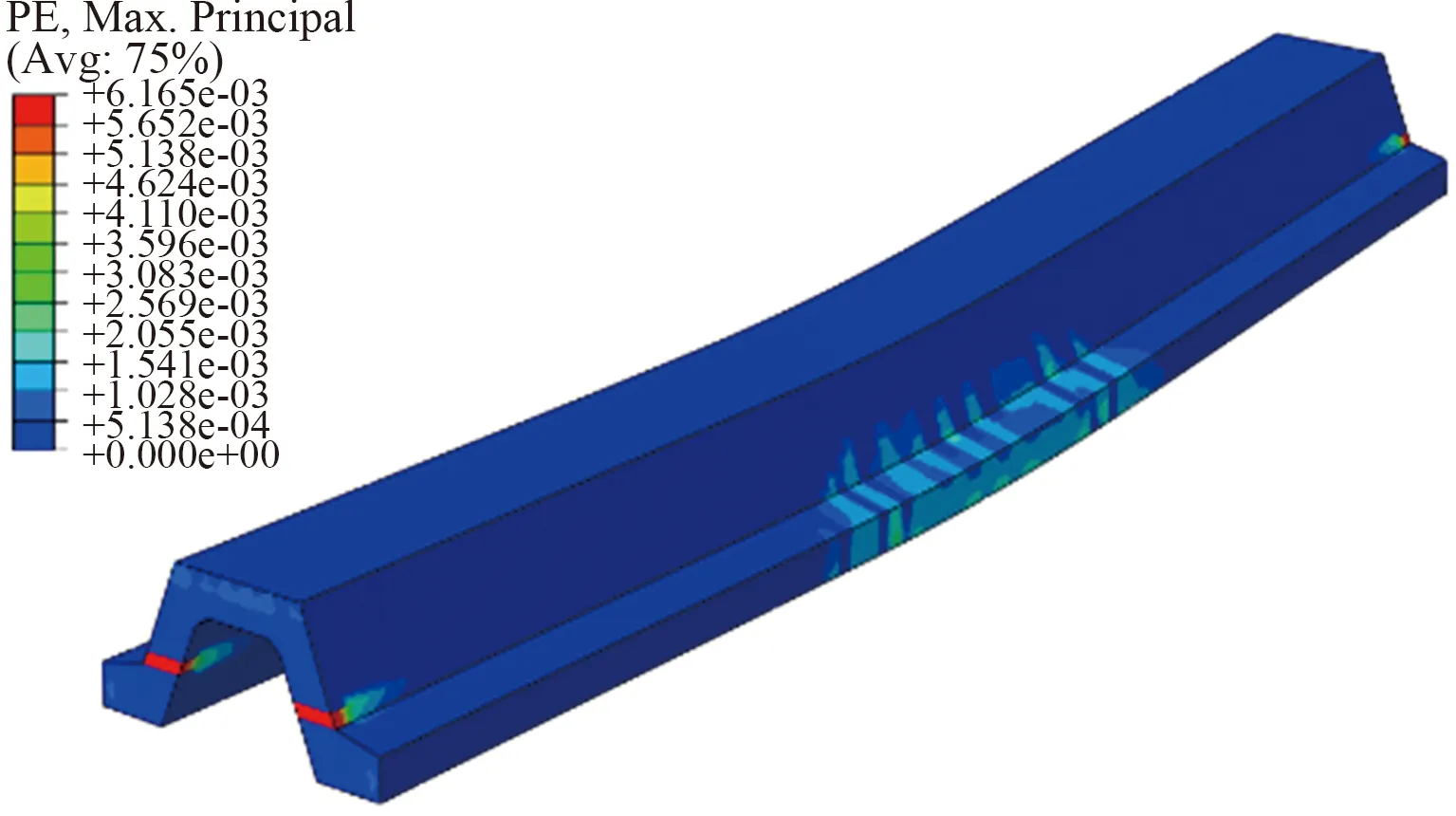
图15 预应力混凝土波形板桩的塑性应变云图
从图14中可以看出,最大拉应力主要集中在纯弯段,这符合试验设计要求。预应力混凝土波形板桩破坏时纯弯段的裂缝开展情况如图6所示,通过对比图15与图16[13]可得,模拟得到的裂缝扩展情况与试验实际观测到的情况相近。

图16 预应力混凝土波形板桩破坏时纯弯段的裂缝开展情况
模拟与试验得到的纯弯段弯矩-加载点挠度曲线如图17所示。由图17知,模拟结果与试验结果的数值相近,且模拟得到的预应力混凝土波形板桩纯弯段弯矩-加载点挠度曲线的变化趋势与试验测得曲线的变化趋势基本一致,说明该有限元方法预测结果具有一定的参考价值。
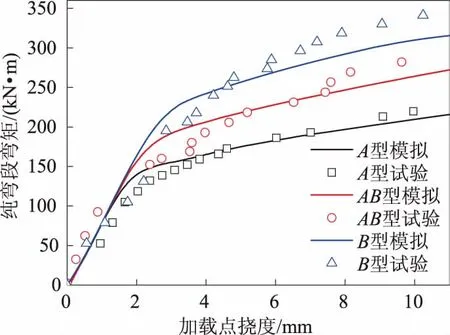
图17 模拟得到的预应力混凝土波形板桩纯弯段的弯矩-加载点挠度曲线
3 理论、试验、有限元结果的对比分析
3.1 纯弯段弯矩-加载点挠度曲线的比较
模型计算时采用表2和表3中的参数,与模拟计算时相同。不同类型预应力混凝土波形板桩的理论计算、试验测定[13]及模拟计算获得的预应力混凝土波形板桩纯弯段弯矩-加载点挠度曲线如图18所示,不同方式得到的该纯弯段弯矩结果见表4。由于裂缝宽度无法计算得到,故采用试验起裂挠度对应的计算弯矩作为抗裂弯矩,试验极限挠度对应的计算弯矩作为极限弯矩。

图18 理论计算、模拟及试验得到的预应力混凝土波形板桩纯弯段的弯矩-加载点挠度曲线

型号抗裂弯矩/(kN·m)理论试验模拟误差分析/%理论模拟极限弯矩/(kN·m)理论试验模拟误差分析/%理论模拟A10614113610.63.52392292184.44.8AB1481641569.84.93183082833.28.1B2002142186.51.93883853280.814.8
通过对比图18中的3条曲线发现,预应力混凝土波形板桩纯弯段的弯矩和挠度的理论计算值与模拟值在受力弹性转折点上均接近于试验值,模拟值偏大;在塑性阶段,该波形板桩纯弯段弯矩-加载点挠度模拟曲线的斜率比理论计算曲线的低;波形板桩纯弯段弯矩的试验值在进入塑性阶段后基本被包含在理论值与模拟值当中,大于模拟值且小于理论值。根据弯矩的误差分析结果知,弯矩的最大误差均不超过15%,且基本在5%以内,在波形板桩的设计中,可通过同时运用模拟计算和理论计算对板桩的抗弯性能进行评价。
3.2 挠度曲线对比
以A型预应力混凝土波形板桩为例,不同纯弯段弯矩下的理论计算与模拟得到的跨间挠度分布曲线如图19所示。
由图19知,在不同荷载下的理论计算挠度分布和模拟所得的挠度分布形状类似且数值相近。挠度曲线为对称弯曲曲线,在荷载较小时,模拟挠度值小于理论计算挠度;而在荷载较大时,模拟挠度值大于理论计算挠度值。在图18(a)中可看到明显的对应关系:经过线弹性转折点后,弯矩较小时,理论挠度大于模拟挠度;弯矩增大到某一值后,理论挠度小于模拟挠度,这是二者计算方式不同导致的结果。

图19 理论计算与模拟所得的跨间挠度分布曲线
4 结语
基于截面等效假定建立了预应力混凝土波形板桩正截面抗弯承载力的计算模型,该模型可计算出波形板桩在受弯过程中的截面抗弯弯矩、中性轴高度以及跨间挠度值。采用上述计算模型对波形板桩四点弯加载进行了计算,并结合数值模拟与试验值进行对照分析,得出以下结论:
1)根据模型计算得到的纯弯段弯矩-挠度曲线的斜率可将波形板桩抗弯过程分为3个阶段:弹性阶段、弹塑性阶段及塑性阶段。截面中性轴高度在这3个阶段中随弯矩的增长率分别表现出基本不增长、迅速增长、逐渐平缓增长的规律;跨间挠度在这3个阶段随纯弯段弯矩的增长率分别表现为:缓慢增长、中速增长、快速增长。
2)经计算,波形板桩抗裂弯矩及极限抗弯弯矩随混凝土截面预应力的增加而增加,但截面预应力的改变并不影响波形板桩弹性阶段及塑性阶段的结构柔度,这与试验得出的规律是一致的。
3)模型计算结果、试验结果与模拟结果吻合良好,三者所得的抗裂弯矩、极限弯矩误差均不超过15%,且基本在5%以内。在相同的计算参数下,波形板桩纯弯段弯矩在塑性阶段的计算值大于模拟值。
[1] 王广宇.预应力混凝土空心方桩成套技术研究[D].北京:中国建筑科学研究院,2007.
[2] LIU Hanlong,CHU Jian,DENG An.Use of large-diameter, cast in situ concrete pipe piles for embankment over soft clay[J].Canadian Geotechnical Journal,2009,46(8):915-927.
[3] 俞峰,张忠苗.混凝土开口管桩竖向承载力的经验参数法设计模型[J].土木工程学报,2011,44(7):100-110.
[4] 蒋元海,匡红杰,钱树青,等.先张法预应力混凝土管桩:GB 13476—2009[S].北京:中国建筑工业出版社,2009.
[5] XING Haofeng,ZHAO Hongwei,YE Guanbao,et al.Effect of driving long pre-stressed high-strength concrete pipe piles in alluvium and its mechanical behavior[J].Bulletin of Engineering Geology and the Environment,2012,71(4):771-781.
[6] ZHOU Mi,LIU Hanlong,HOSSAIN M S,et al.Numerical simulation of plug formation during casing installation of cast-in-place concrete pipe (PCC) piles[J].Canadian Geotechnical Journal,2016,53(7):1093-1109.
[7] 董金玉,刘召善,王国华,等.桩承载力自平衡试验法在某桩基工程中的应用[J].华北水利水电大学学报(自然科学版),2015,36(1):55-60.
[8] 中国建筑科学研究院.建筑桩基技术规范:JGJ 94—2008 [S].北京:中国建筑工业出版社,2008.
[9] 中国建筑科学研究院.预应力混凝土空心方桩:JG 197—2006[S].北京:中国建筑工业出版社,2006.
[10] 张后禅.U形预应力混凝土板桩[J].中国水利,2010(21):67.
[11] 刘林,陈永辉,陈龙.U形预应力混凝土板桩现场试验研究[J].低温建筑技术,2014,36(12):106-108.
[12] 过镇海.混凝土的强度和本构关系:原理与应用[M].北京:中国建筑工业出版社,2004.
[13] 范向前,孙岳阳,王洋.先张法预应力高强混凝土波形板桩结构材料试验与理论分析[R].南京:南京水利科学研究院,2016.
CalculationModelandAnalysisofPrestressedHighStrengthConcreteU-shapedSheetPileunderBendingLoad
HU Shaowei1,2, HUANG Yiqun1,2, FAN Xiangqian1
(1.Material and Structural Engineering Department, Nanjing Hydraulic Research Institute, Nanjing 210029, China;2.College of Mechanics and Materials, Hohai University, Nanjing 211100, China)
The prestressed concrete U-shaped sheet pile has a strong application prospects as a new type of foundation pit supporting structure, and it has the characteristics of big earth-retained area, beautiful shape and so on. For prestressed high strength concrete U-shaped sheet pile, flexural capacity and strain are the key to design.To study the flexural mechanical properties of prestressed high strength concrete U-shaped sheet pile, a calculation model of the cross-section flexural capacity of U-shaped sheet pile under bending load was established based on the equivalent section, the height of neutral axis, bending moment of section, section curvature and deflection could be calculated through the calculation model, and the simulation with finite element method was carried out to verify the rationality of the model. The results show that the model calculation results are in good agreement with the experimental results and the simulation results, and the error of crack-resistant moment and the limited bending moment has been controlled below 5%.
prestress; concrete; U-shaped sheet pile; flexural capacity; bending moment-deflection curve
杜明侠)
TV332;TU473
A
1002-5634(2017)06-0001-08
2017-07-20
国家杰出青年科学基金项目(51325904);国家重大科研仪器研制项目(51527811);国家自然科学基金项目(51309163,51409162,51679150);江苏省自然科学基金资助项目(BK20140081);水利部公益性行业专项经费项目(201501035)。
胡少伟(1969—),男,河南杞县人,教授级高级工程师,博导,博士,从事工程损伤断裂、组合结构等方面的研究。E-mail:hushaowei@nhri.cn。
10.3969/j.issn.1002-5634.2017.06.001
