基于灰色关联分析法的汽车后视镜优化模型

2018-01-02王正坤赵世宇

信息记录材料 2018年2期

关键词：后视镜镜面畸变

王正坤，王鹏，赵世宇

（山东科技大学山东青岛 266590）

基于灰色关联分析法的汽车后视镜优化模型

王正坤，王鹏，赵世宇

（山东科技大学山东青岛 266590）

行车司机能够通过汽车后视镜观察到的视野范围、以及镜面成像的畸变情况对于行车安全具有重要的意义。为了尽可能改良汽车后视镜的设计，市面上推行一种变曲率后视镜。本文主要探讨在镜面外形及尺寸优化方案的设计中，自变量镜面曲率半径、镜面宽度与因变量视野范围、畸变情况的关系。将抽象的视野量化为视角，使其能用数学的语言和符号来进行计算和分析。对于多维的物体畸变，则简单地用二维的成像大小变化来进行估测。根据镜面成像原理，建立模型并与MATLAB软件应用相结合，选出几组相对较优的设计方案组合。对于所得的多个方案，采用灰色关联分析法，根据灰色加权关联度的排序，可选出最优镜面优化方案。

量化；灰色关联分析；视野角度；畸变

1 引言

汽车后视镜的视野范围与图像畸变对行车安全非常重要，增大视野范围可减小司机的视野盲区，扩大道路状况的可视范围；图像畸变可能会使物体在成像时形状、大小等发生改变，使司机难以准确判断后方物体的形状和物体与自己的间隔距离。为增大后视镜的视野范围，可使用凸面镜代替平面镜做汽车的外后视镜，但图像会产生畸变。为兼并平凸两种镜面的优点，可以在内侧使用曲率半径较大、接近于平面镜的凸面镜，外侧使用曲率半径较小的凸面镜，既保证视野较大，又使得离车辆横向距离较近的物体畸变较小。

2 优化方案的设计

2.1 视野的量化以及量化后汽车后视镜视角的计算

图1所示为水平面上由凸面镜的曲率半径R以及镜面宽度w所确定的水平方向的视角，图中s为眼点到凸面中心的连线距离。图中所示的入射线与反射线定义了在图示中的眼点位置以及凸面镜大小下镜面所能反射到的最大视角范围，即入射线与水平轴线所成夹角角度的二倍，设该角度为θ，可得计算θ的公式为：

图2所示为凸面镜偏离水平轴线的情况。此时凸镜位于与眼睛与镜面中心连线成λ角度的位置。对眼睛来说，凸镜在宽度上的减小因数为cosλ，由此将上式改写为：

图2中表示沿车辆纵向从眼点到穿过镜面中心的横向轴线的距离；表示沿车辆向从驾驶员眼睛到通过镜面中心纵向轴线的距离。由此可得：

2.2 图像畸变与曲率半径关系的计算

由成像原理图3可知单个折射球面的物像位置关系计算公式为

此处引入垂直放大率的概念。垂直放大率是探明光学系统成像规律的重要参量，用来描述物体实际高度和成像高度的关系。一般用β来表示凸面镜的垂直放大率。因此可以用垂直放大率来描述凸面镜成像的畸变率。

已知凸面镜成正立、缩小的像，因此垂直放大率的范围应为0＜β＜1，当β值越大时，垂直放大率越大，成像的畸变率越小，当β值越小时，垂直放大率越小，成像的畸变率越大。

在图3中ΔABC～ΔA'B'C'，因此

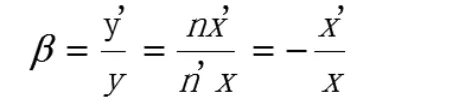
可得出垂直放大率与曲率半径的关系，从而得出成像畸变率与凸面镜曲率半径的关系，即β=1/(1-2x/R)

2.3 灰色关联分析

（1）确定比较对象（评价对象）和参考数列（评价标准）。

评价标准的选取共有三个，即视野范围、垂直变化率和畸变率。

已知畸变率与垂直放大率成负相关关系，设比例系数为η，则存在关系：μ=η/β

为了便于计算分析具体数值，将η视为1来处理，即认为畸变率与垂直放大率成反比。

以视野范围、垂直变化率和畸变率为优化指标。

（2）确定各指标值对应的权重，可用层次分析法等确定各指标对应的权重为ω=[ω1，ω2，ω3]

其中ωk(k=1,2,3)为第k个评价指标对应的权重。

（3）计算灰色关联系数

（4）计算灰色加权关联度,计算公式为

（5）评价分析

根据灰色加权关联度的大小，对各比较对象进行排序，关联度越大，其评价结果越好。

其中ρ∈[0,1]为分辨系数，这里可以取ρ=0.5。计算外侧凸面镜ζi(k)及ri具体数值。

3 检验外侧凸面镜对视野的改变

在后视镜镜面总长度为400mm，总宽度为200mm的情况下，通过计算视野范围、垂直变化率和畸变率可以得到几种可能的方案，再通过灰色关联分析得到最优方案为外侧凸面镜R=350mm，镜面宽度为65mm，镜面其它部分使用平面镜。将宽度和曲率半径代入公式中得出该镜面的视野范围为21.34°，后视镜外侧使用所选凸面镜后水平视野相比于使用平面镜增大了10.67°。