静电场中的镜像电荷对偶方法

蒋铭阳

（成都七中嘉祥外国语学校 四川 成都 610000）

静电场中的镜像电荷对偶方法

蒋铭阳

（成都七中嘉祥外国语学校 四川 成都 610000）

通过库仑定律研究静电场问题，基本出发点是电荷的带电量无限集中于一点，两电荷之间受力的规律与物体间的万有引力形式上是统一的，从这个形式出发，可以采用相似的方法研究点电荷的受力规律，质点与点电荷对等，本文在此基础上引入虚拟的镜像电荷，按照电场叠加等效的原则，利用边界条件认识镜像电荷的物理意义，有助于研究静电场中感应电荷电场分布。

静电场；库仑定律；镜像电荷；感应电荷

本文讨论了几种不同的场景，通过研究静电场中电荷分布的规律，引入了像电荷的观点，像电荷是虚拟的电荷，具有数学上的意义，同时根据电场可以叠加的原理，镜像电荷并未改变局部电场的分布，即像电荷也具有其特定的物理意义。从存在性上讲，引入像电荷是为方便计算而来，它并不存在，但引入像电荷之后，静电场可以看着是原电荷和像电荷的矢量叠加，根据静电场的叠加原理，可以分别求出原电荷和像电荷在空间某点处产生的库仑力，方便了问题的分析和计算。

先考虑一个点电荷与一个接地金属导体球组成的系统，这个系统就是由质点与非质点物体构成的，不能像对两个简单的质点之间的分析一样。由于库仑定律表达式

有类似的形式，考虑到在处理质点与均匀球体之间万有引力时采用的是等效的方法，即将质点对均匀球体的力等效在等效作用点（球心）上，在对一个点电荷与一个接地金属导体球组成的系统进行分析时，可以采用类似的等效法，从而转换为较为方便的、对两质点的分析。需要注意的是，当我们分析万有引力时，将球体的总质量等效为一个质点，不影响球体之间的万有引力的关系。球体的质量分布是不会因质点的存在而改变的，但分析金属球体时，其表面会不均匀地带上感应电荷，可以肯定的是，这个等效点不再是球心。

根据这种对应的形式，本文考虑了点电荷模型，其中点电荷在球壳外，点电荷在球壳内三种场景，讨论应用静电荷中基本定律，求解电场问题的一般方法，在此基础上用虚拟的像电荷等效的概念，将球壳等效为一个未知电量及位置的点像电荷。

为了方便分析，先考虑以下模型：

空间中存在的两个点电荷，相距为d，分别带电+Q与-q。此时理论上可以画出空间中电场线以及等势面，为方便起见，先考虑以无穷远为零电势时电势为零的等势面。若重叠于等势面放置一块金属接地薄板，可以肯定，空间中电场线、等势面分布不会发生改变，金属板所分割成的两个空间的电场因静电屏蔽而不变。此时可以发现撤去一个电荷，另一个电荷所在的分割后的空间电场仍不会变化。

下面对这个等势面进行分析。

利用点电荷在空间中产生的电势U与距点电荷的距离R的关系

以及电势的叠加原理，得到空间中任意一点、距+Q、-q分别为R、r的一点（由于此系统具有二维对称性，所以确定两个坐标量就可以确定该点情况）电势为

建立，以-q为原点，-q指向+Q方向为x轴正方向的坐标系，在二维坐标内一点（X，Y)到两点距离关系有：

由于X2、Y2的系数相等，故上述方程轨迹为一个圆，推广到三维坐标系中，将会形成一个球。在此基础上，可以反向利用该结论，即一个点电荷与一个接地金属导体球组成的系统在球外产生的电场可以等效为两个点电荷的合作用，只是等效的那个电荷的位置和带电量尚未确定。以下将讨论其确定方法。

在此基础上，用以下方法求解：

如图1所示，以球心为原点，考虑一个过球心、实际存在的+Q、虚拟的-q的一个面

图1 镜像电荷计算闭合曲面模型

设-q（x，0），由两个点在球表面上任意一点合电势为零，考虑离+Q最近的球面上的点和离+Q最远的球面上的点电势为零，可以列出下列式子

由上述模型可以发现，金属球壳可以将空间分为两个相互独立的两部分，起到了静电屏蔽的作用，实际上点电荷在金属球壳内产生的场强仍然遵循库仑定律，并没有消失，只是被球壳带的感应电荷所产生的合场强所抵消了。在此基础上，可以知道球壳内一点的电势表达式：

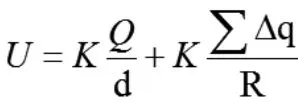
也就是说球内表面所带总电荷量就等于球壳内像电荷所带电荷量，这符合对感应电荷的认知。即电荷不会凭空产生，也不会凭空消失。

通过以上的讨论，在静电场中，电荷是感应出来的，感应现象只是改变了原有电荷的分布，可见电荷总代数和始终是守恒的，镜像电荷的引入，只是一种数学方法，并没有改变物理定律的普遍适用性。

以下对该模型进行讨论

由q、x的表达式可知，q、x均趋近于零，其意义是金属球足够小的情况下，对空间电场分布几乎没有影响，类似于质点是质量的无线集中，在万有引力定律中，将质量集中在一处，也不会改变物体之间的万有引力的大小。在坐点电荷近似后，可以忽略其存在。此处有明确的物理意义，这种近似也是比较合理的。

可以知道此时的像电荷相当于在距球心无限远处放一个电荷，而球心也在无限远处，无法直接分析，为了分析这种情况，先借助以下模型进行分析

空间中存在相距为2L的电荷+q、-q，类似于上面的模型，根据分布的几何对称性，易知此时的零等势面为垂直于两电荷连线的中垂面，是一个平面。在该平面上，原电荷和镜像电荷激发出来的电场，大小相等，方向相反，可以等效为接地面。同样地若在这个平面处放上一块接地金属板，将会把空间分为两个互相独立的部分，且两部分关于金属板对称。于是易得+q、-q可以互为像电荷，而且此时的金属板为无限大平面，可以认为是圆心在无限远处、半径无穷大的球的对应立体角极小的球冠，当对应的圆心角足够小时，每一段弧线就是一段线性微元，满足可积分的条件，这正是所讨论的的情况。

反过来再看q、x的表达式

同理

此结论与上述分析相符。

上述推导过程中，用到了多项式展开的泰勒公式，作为合理的近似，截去高阶无穷小量，仅保留前两项。

在此基础上，理论上可以得到点电荷与无限大接地金属平板组成的系统在空间中产生的电场，这里按照金属板表面附近的电场分析金属板上电荷分布。

由于该系统具有二维对称性，其中y轴在金属板上，x轴通过像电荷与点电荷连线的场景。

分析y轴上一点，设此点与点电荷q的连线与x轴夹角为θ，此点的电场强度

考虑一个以原点为圆心的位于金属板上的一个极细圆环，其宽度对应q处的夹角为dθ微元。

环上任意一点与电荷的连线与x轴夹角可以认为是不变的，均为θ，可以得到此圆环的面积

对此圆环运用高斯定理，取一个封闭曲面即圆环柱，其高度很小，可以得到

解得

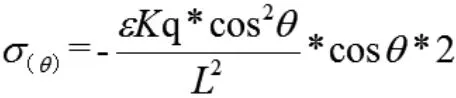
此时已经得到平板作为一个非质点物体的带电面密度关于θ的关系，说明平板的带电情况已经确定，在此基础上，可以求出平板的带电总量

代入σ(θ)、dS的表达式，将上式写为积分形式

求出金属平板的总带电量为-q，同样可以利用之前点电荷在球壳上产生的感应电荷的结论，只不过这个球壳半径无穷大，其总的感应电荷为-q，是符合之前的结论的。

（3）点电荷在金属球壳内

由于之前的模型中被球壳分割的两部分互不影响，所以接地球壳内的点电荷的像电荷为以点电荷作为像电荷在模型“点电荷在球壳外”中所对应原来的电荷。设此时点电荷带电量为q，接地球壳半径为R，点电荷距球心距离为x，像电荷距球心为d，带电量为Q，有

由此确定了像电荷大小以及虚拟的位置。

①镜像电荷使用需要注意的几个问题：

②镜像电荷不能和原电荷在同一侧，否则就不是镜像电荷了；

③镜像电荷和原电荷产生的场，在边界处不改变原来的场线的分布；

④系统总的电荷代数和要守恒；

⑤镜像电荷一般处于与原电荷对称的位置，但不绝对；

⑥镜像电荷的个数可能不唯一；

本文从三个不同的场景分析了镜像电荷的位置和大小的确定方法，总的原则是从系统总的电荷量代数和不变出发，感应电荷只是改变了正负电荷的分布，其总量不变。根据高斯定理，电场属于有源场，即任意一个闭合曲面内无点电荷源，则电通量为0。研究感应电荷的分布时，这个视角可以提供一种方便的分析方法。对于非点电荷的情形，用微元法思想，结合积分等数学工具进行分析，电场力适用矢量的分解与合成，对于更加复杂的情形，分解成本文总结的三种特殊情形后，再矢量叠加即可；本文讨论了一种普遍的分析方法。

像电荷等效的本质是电场的叠加性，通过模拟等效电场，从数学意义上引入了一个位置上对称的点电荷，在用像电荷替换掉球壳之后，电场的分布和大小并未发生变化，但像电荷相当于把电场源等效为一点，这样场的问题就简化为了两个点电荷的矢量叠加，点电荷适用的库仑定律在此情景下就简便很多。

[1]喻莉，杨植宗，何艳.线电荷与圆柱导体间的相互作用[J].物理通报，2011(2)：15-16.

[2]储礼悌.静电场分析[M].天津科学技术出版社，1984.

[3]劳(Rao.N.N.工程电磁学基础[M].机械工业出版社，2006.

[4]李岳鹏.求解镜像电荷的一种简便方法[J].唐山师范学院学报，2003，25(5)：26-27.

[5]汪映海，杨双强.点电荷和介质球系统的镜像电荷分布[J].物理，1986，15(12)：0-0.

TP319 【文献标识码】A 【文章编号】1009-5624（2018）02-0104-03