飞行器偏置制导律研究*
2018-01-02高静金玉华
高静,金玉华
(中国航天科工集团 第二研究院, 北京 100854)
0 引言
目前,空间目标上某些昂贵的、难以获取的零部件可利用冷喷涂工艺来进行修复。冷喷涂工艺是将粉末以超音速冲击受损零件表面,然后在基体表面形成牢固附着的致密的固体材料,从而使零件恢复到原来的尺寸。但这种目标的表面感性/修复需求的提出,对飞行器的制导律提出了更高要求。在修复受损目标表面任务中,需要飞行器从目标旁偏置一段距离,且在偏置过程中提出终端角约束的需求。
目前针对带有撞击角约束的制导控制问题研究不多,其中比例导引形式的设计方法应用普遍,比例导引要求发动机提供的推力是变化的,但大多数研究都未考虑到轨控发动机不能提供变推力的工作原理,只进行了理论分析。Kim和Grider[1]在1973年首次提出将偏置比例导引应用于解决终端角度约束问题,在二维平面内研究了带撞击角约束的比例导引律,在传统比例导引的基础上添加了一个随时间变化的偏置项,从而实现终端攻击时期望角度的约束。Jeong[2]等人在Kim的基础上进一步进行讨论,提出了一种更为简洁的制导形式。上述2种导引律均针对固定目标,不依赖于剩余时间的估计。考虑到垂直打击场景下存在导弹驾驶仪动态因素和重力影响的问题,曹邦武和翁兴伟[3-4]设计了一种能垂直命中目标的偏置比例导引律,但该方法需要获取视线角加速度项和目标的切线加速度,目前难以在实际工程中推广应用。顾文锦[5]通过对虚拟目标的跟踪来实现末段有角度约束的攻击,设计了一种比例导引律。针对导弹速度非定常情况下的制导问题,马国欣[6-7]提出了一种满足攻击时间和攻击角度约束的制导律,该导引律可用于多导弹协同问题。
针对冷喷涂工艺修复受损目标表面的需求,本文提出了一种改进的偏置比例导引律,在考虑到轨控发动机只能提供常推力、能多次启动的实际工作状态,对同时满足终端角约束和实现距离偏置的制导律开展研究。
1 导引律设计
1.1 基本假设[8-9]
(1) 将飞行器和目标看作是同一平面内运动的质点。
(2) 目标速度为常量,水平面速度始终为0;且目标速度倾角为0。
1.2 带有碰撞角约束的二维超前比例导引律设计
如图1所示,基于以上假设条件,俯仰平面内飞行器和目标交会模型可由以下微分方程组表示[10-12]:
(1)
(2)
(3)
传统的偏置比例导引律为
(4)
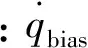
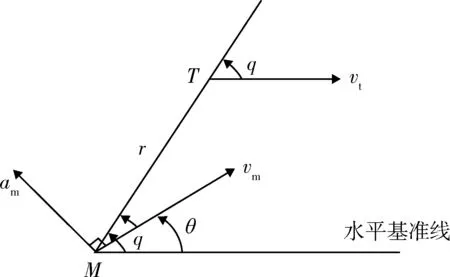
图1 未制导俯仰平面内几何关系Fig.1 Geometry in the vertical plane during terminal phase
(5)
式中:vx为飞行器速度沿视线方向分量;η为一个大于0的常量;N为导引系数。
因此,指令加速度可表示为
(6)

图2 二维平面内视线角与期望角之间的几何关系Fig.2 Geometry relations between LOS angle and expected angle in the two dimensional plane
若要在满足终端碰撞角约束的条件下同时解决测量目标点和瞄准点不重合的问题,还需在偏置项中添加距离项。如图3所示,M为飞行器质心,T′为飞行器的目标点,T为飞行器的的瞄准点,q为飞行器质心与目标点连线的视线角,r为飞行器质心与目标点距离,q1为飞行器质心与瞄准点连线的视线角,r1为飞行器质心与瞄准点距离,目标点和瞄准点之间的距离T′T=h,即偏置距离。其中T′T与目标速度方向一致即本文的瞄准点T必须在目标速度矢量上[13-15]。
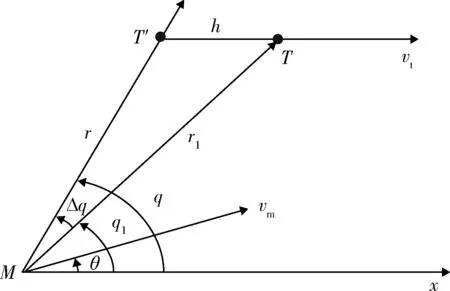
图3 目标点和瞄准点之间的几何关系Fig.3 Geometry relations between target point and aiming point
由图3可得到以下几何关系:
rsin Δq=hsinq1,
(7)
r1sin Δq=hsinq,
(8)
r1cosq1=rcosq+h,
(9)
r1cos Δq=r+hcosq,
(10)
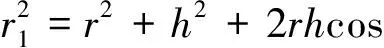
(11)
对式(7)求导有
(12)
再将式(8)~(10)代入式(12)有
(13)
简化得
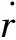
(14)
即
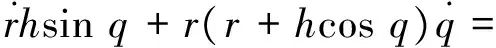
(15)
则有
(16)
因此最终指令加速度为
(17)
1.3 轨控发动机工况
轨控发动机布局如图4所示,在不考虑推力偏心和质心漂移的情况下,本文研究俯仰平面内相对运动,因此只有1,3号发动机工作。
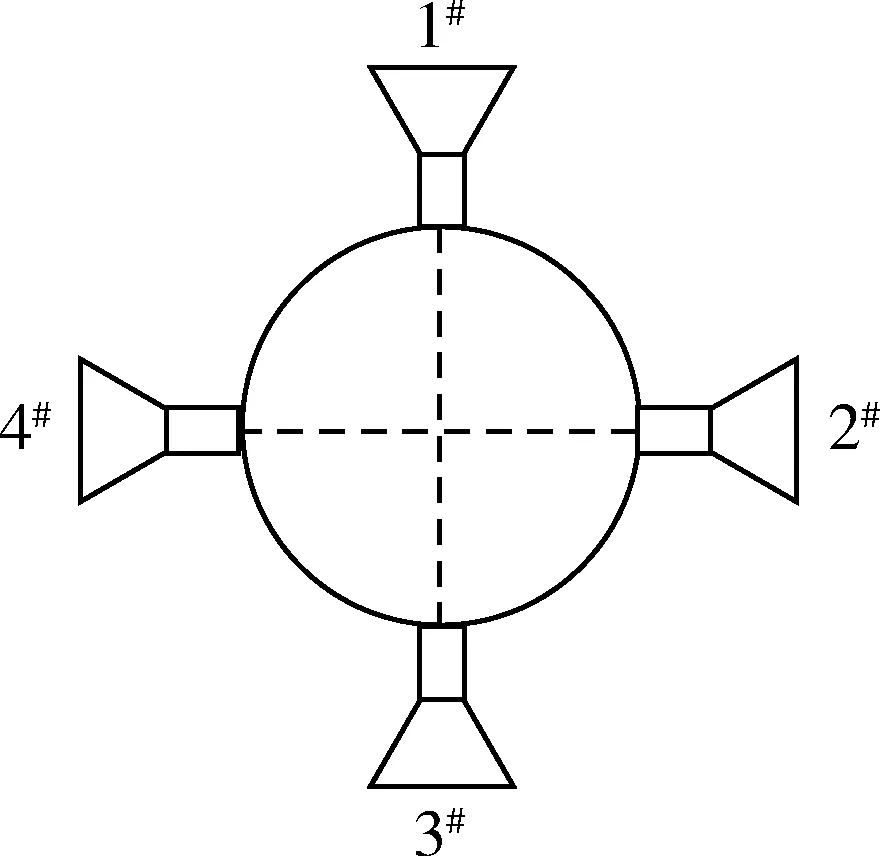
图4 轨控布局(从尾部看)Fig.4 Divert thruster layout(viewed from tail)
本文为提高轨控发动机燃料消耗效率,在考虑到当前轨控发动机的上个周期开关指令和上两个周期的开关指令状态基础上通过动态调节3个发动机阈值确定当前发动机的开关状态。
2 仿真校验
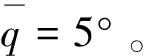
仿真结果如图5~10所示。

图5 相对距离r和r1变化曲线Fig.5 Variation curve of relative distance r and r1

图6 相对距离r和r1终端变化曲线Fig.6 Terminal variation curve of relative distance r and r1
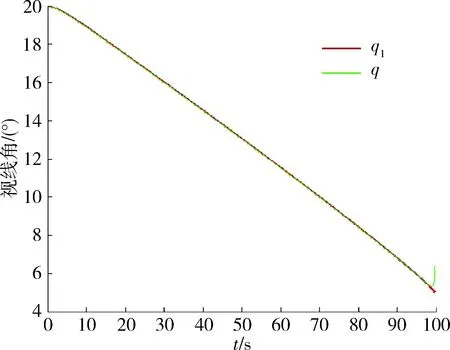
图7 视线角q和q1变化曲线Fig.7 Variation curve of LOS angle q and q1
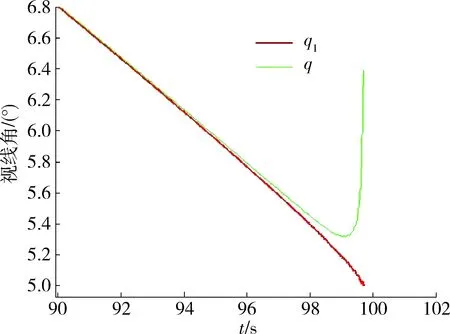
图8 视线角q和q1终端变化曲线Fig.8 Terminal variation curve of LOS angle q and q1
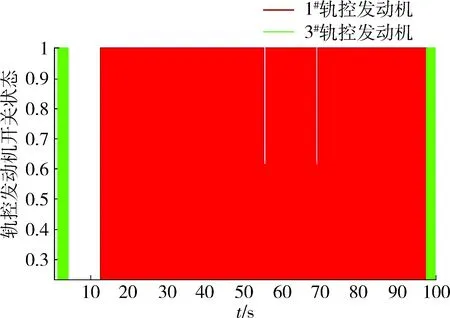
图9 轨控发动机开关状态曲线Fig.9 On and off curve of divert thruster

图10 轨控发动机终端开关状态曲线Fig.10 Terminal on and off curve of divert thruster
3 结论
通过数字仿真,可得以下结论:
(1) 仿真结果显示对瞄准点T的脱靶量为0.320 3 m,成功实现距离的偏置并且满足对命中精度的要求,对探测点T′的脱靶量为10.030 3 m,两者相差近似等于偏置距离h。
(3) 由轨控发动机的开关曲线可以看出,最后要命中目标过程中轨控发动机开关次数明显增加,这是因为在剩余距离为几十米时所需的指令加速度增长速度很快。
(4) 本文提出的偏置制导律是精确有效的,能较好地满足偏置距离和落角约束双重要求。
本文仅在俯仰平面内对同时满足终端攻击角约束和实现与目标速度方向一致的距离偏置的制导律开展分析探讨,三维平面内的制导律正在进一步研究。
[1] KIM M, GRIDER K V. Terminal Guidance for Impact Attitude Angle Constrained Flight Trajectories [J]. Aerospace Electronic Systems, IEEE Transactions on, 1973,9(6):852-859.
[2] JEONG S K, CHO S J. Angle Constraint Biased PNG[C]∥5th Asian Control Conference Melboume, Austrilian, 2004:1849-1854.
[3] 曹邦武,姜长生,关世义.电视指令制导空地导弹垂直命中目标的末制导系统研究 [J]. 宇航学报, 2004,25(4):393-397.
CAO Bang-wu, JIANG Chang-sheng, GUAN Shi-yi. Research on the Vertical Intercept Terminal Guidance System of TV-Command-Guidance Air-to-Ground Missile[J]. Journal of Asrtonautics, 2004,25(4):393-397.
[4] 翁兴伟,黄长强,刘子阳.无人攻击机垂直命中目标的末制导律研究 [J].兵工学报, 2008,29(2):184-187.
WENG Xing-wei, HUANG Chang-qiang, LIU Zi-yang. Study on the Terminal Guidance Law of Hitting the Target Vertically for UCAV [J]. Acta Armamentarii, 2008,29(2):184-187.
[5] 顾文锦,雷军委,潘长鹏.带落角限制的虚拟目标比例导引律设计 [J] .飞行力学, 2006,24(2):43-45.
GU Wen-jin, LEI Jun-wei, PAN Chang-peng. Design of the Climbing Trajectory Using Virtual Target’s Proportional Navigation Method with the Control of Terminal Azimuth of A Missile [J]. Flight Dynamics, 2006,24(2):43-45.
[6] ZHANG You-an, MA Guo-xin. Guidance Law with Impact Time and Impact Angle Constraints [J] . Chinese Journal of Aeronautics,2013,26(4):960-966.
[7] 马国欣.张友安.导弹速度时变的攻击时间与攻击角度控制导引律 [J].飞行力学, 2013,31(3):255-259.
MA Guo-xin, ZHNAG You-an. Impact Time and Impact Angle Control Guidance Law for Missiles with Time-Varying Velocity [J]. Flight Dynamics, 2013,31(3):255-259.
[8] 李朝旭, 郭军, 李雪松. 带有碰撞角约束的三维纯比例导引律研究 [J]. 电光与控制, 2009,16(5):9-12.
LI Chao-xu, GUO Jun, LI Xue-song. Study on Three-Dimensional PPN with Impact Angle Constraints[J]. Elecrtonics Optics & Control, 2009,16(5):9-12.
[9] 钱杏芳, 林瑞雄, 赵亚男, 等. 导弹飞行力学[M]. 北京: 北京理工大学出版社, 2012.
QIAN Xing-fang, LIN Rui-xiong, ZHAO Ya-nan, et al. Missile Flight Aerodynamics [M]. Beijing: Beijing Institute of Technology Press, 2012.
[10] KM B S, SEO J H. The Realization of the Three Dimensional Guidance Law Using Modified Augmented Proportional Navigation [C]∥Proceedings of the 35th Conference on Dicision and Control , Kobe, Japan, 1996(3): 2707-2712.
[11] SRIVASTAVA R, SARKAR A K, GHOSE D, et al. Nonlinear Three Dimensional Composite Guidance Law Based on Feedback Linearization [C]∥AIAA Guidance, Navigation, and Control Conference and Exhibit, 2004, Providence, Rhode Island, AIAA 2004-4903: 1-11.
[12] PAUL L V, RANDALL K L. Target Acceleration Modeling for Tactical Missile Guidance [J]. Journal of Guidance, Control and Dynamics, 1984,7(3) : 315-321.
[13] 陆毓峰, 施志佳. 超前偏置导引律的探讨 [J].弹道学报, 1992(11):30-39.
LU Yu-feng, SHI Zhi-jia. The Study of Proportional-Navigation Guidance Law for Leading of Impact Point [J]. Journal of Ballistics,1992(11):30-39.
[14] 陆毓峰, 施志佳. 超前偏置比例导引律及其实现方法 [J]. 航天控制, 1992(4):1-8.
LU Yu-feng, SHI Zhi-jia. Proportional Navigation Guidance Law for Leading of Impact Point and Its Implement Method [J]. Aerospace Control, 1992(4):1-8.
[15] 施志佳, 陆毓峰, 张殿祜.一种能实现超前偏置的比例导引律 [J].西北工业大学学报,1993,11(2):189-192.
SHI Zhi-jia, LU Yu-feng, ZHANG Dian-hu. A Proportional Navigation Law for Improving Target-Finding Accuracy to Very Small Tactical Missile [J]. Journal of Northwestern Polytechnical University, 1993,11(2):189-192.
