大动态光纤陀螺及其应用*

王磊，陈杏藩，刘承，舒晓武

(浙江大学a.光电科学与工程学院； b.光学惯性与传感国防重点学科实验室，浙江 杭州 310027)

0 引言

运动载体中，导引头的视线稳定[1-2]是高精度追踪的基础；载体的姿态、速度和位置信息的解算也同样是高精度导航的前提。而对于高速旋转载体，沿着横滚方向的旋转，带来了其他方向上的耦合，严重影响视线稳定和姿态精度。

为了消除载体扰动的影响，一般采用稳定平台来实现视线稳定。随着弹载对高精度、小型化的需求，捷联式的稳定平台或回路逐渐成为研究的热点[3]。但是，与平台式相比，高速旋转的捷联系统对角速度传感器的要求更加苛刻。旋转导弹、火箭弹的旋转速度高达1 500 r/min[4-6]，常规陀螺仪无法同时满足测量范围和测量精度的要求。为了解决这一问题，许多学者采用了折中的方案。文献[7]，通过半捷联模拟控制减旋电路设计，在横滚方向上不捷联，当载体旋转时内框反方向运动，从而降低对陀螺仪的动态范围的需求；文献[8-9]，则采用六加速度计配置方式，结合力学编排和解算，代替角速度陀螺仪，提高系统的抗过载能力。这些方案仍存在陀螺精度、系统复杂度和可靠性等问题。

针对高速旋转载体视线稳定和惯性导航的特点，本文介绍了光纤陀螺的基本原理，在此基础上提出大动态光纤陀螺，并讨论该型陀螺在系统中的应用特点。该型陀螺具有测量范围大、精度高、稳定性好和系统配置简单等特点，大大提高了姿态测量精度、减小了系统的复杂度，为弹体高速自旋提供一个有效的检测方案[10-12]。

1 大动态光纤陀螺基本原理

光纤陀螺理论基础为光学Sagnac效应[13]：当环形干涉仪在惯性空间转动时，干涉仪干涉回路中沿不同方向传播的两束光之间将附加产生一个正比于转动角速度的光相位差。通过检测该相位差，可推算干涉仪所在系统相对惯性空间的转动角速度大小。根据Sagnac原理光纤陀螺中转动角速度Ω和旋转产生的光相位差ΔφR之间的关系式为

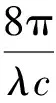
(1)

式中：λ为光波长;c为光在真空中传播的速度;S为光纤环线圈等效面积矢量，方向为等效面积的法线方向;Ω为输入角速度矢量,点乘表示只有投影在等效面积方向的角速度分量才会在干涉仪中产生光相位差。

当有角速度输入时，数字闭环光纤陀螺示意图如图1所示。通过相位调制器(MIOC)和时延差分调制施加一个与Sagnac相位差ΔφR大小相等、符号相反的附加相位差ΔφF，将相位差抵消，使陀螺工作在0工作点位置。

图1 数字闭环光纤陀螺系统构成示意图Fig.1 Illustration of digital closed loop fiber gyroscope

(2)

由于2束光的干涉响应和ΔφR成余弦关系，为保证两者之间的单值对应关系，一般取零点堆对称的单值区间作为陀螺的最大测量范围Ωπ，对应为了[-π，+π]的相位区间，表示为

(3)

式中：L位光纤环中心光纤长度;D为径光纤环的直径。

陀螺的动态范围定义为陀螺最大探测相位差和最小相位差的比值对数值:

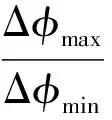
(4 )

典型的光相位灵敏度范围为0.1～10 μrad，对应系统的动态范围在110～150 dB。

由式(4)可以看出，提升陀螺动态范围的有效手段是减小最小检测相位差和扩大最大探测相位差。前者受系统增益和检测电路特性限制，可认为是个常值，而本文采用了后种方案，重点解决增加探测的相位差带来的非单值问题。利用不同级次各级条纹光强的差异性，解调出探测器的直流分量来判断条纹级次；并结合四态方波调制实现在工作

点变化时对级次计数，解算出闭环相位差，拓宽陀螺的动态范围。

改进后的闭环表达式简化为

ΔφR+ΔφF+2nπ≈0,

(5)

式中：n为陀螺工作的条纹级次，n=0，±1，±2，…。

从系统闭环控制角度，不论Sagnac相位差多大，只要能够保证总相位差为0成立，都会被伺服控制在0附近，获得相应的旋转角速度。只是当相位差超出±π时，工作0点在其他级次处。因此，大动态光纤陀螺的技术实现可以归为对条纹级次n的判断和计数。图2是陀螺跨条纹工作的示意图，当相位差超过π时，陀螺的工作点移到更高一级条纹中。

图2 陀螺跨条纹工作的示意图Fig.2 Illustration of gyroscope working on multiple fringes

此时，动态范围公式(4)也相应变为

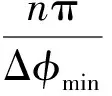
(6)

受光纤陀螺宽谱干涉对比度的限制，理论上条纹级数n可以取到40以上，最大可测量角速度超过40 000 (°)/s。

2 性能评估

陀螺的主要指标包括静态精度(零偏稳定性)和动态性能(标度因数误差)。静态性能的评估遵循国军标光纤陀螺测试方法，采用10 s平滑的方法，零偏稳定性达到0.5 (°)/h，

应用场合的大角速率特点，对陀螺的动态性能更加依赖。动态性能主要由将陀螺数字量与物理量之间的比例关系——标度因数特性和带宽决定。标度因数误差包括非线性和标度因数稳定性。评估采用单轴高速率转台并结合高精度标度因数测试系统，可以实现高达24 000 (°)/s的测量范围以及全速率范围优于5×10-6以下的测量精度。

结合图3和图4可以看出，该型光纤陀螺标度因数全速率非线性度误差小于1×10-5，可测量的速率达到21 600 (°)/s。另外，通过50 d的断电重复性测试，标度因数重复性为3.2×10-5(3σ)，具有较好的稳定性。

图3 陀螺标定曲线Fig.3 Calibration curve of gyro

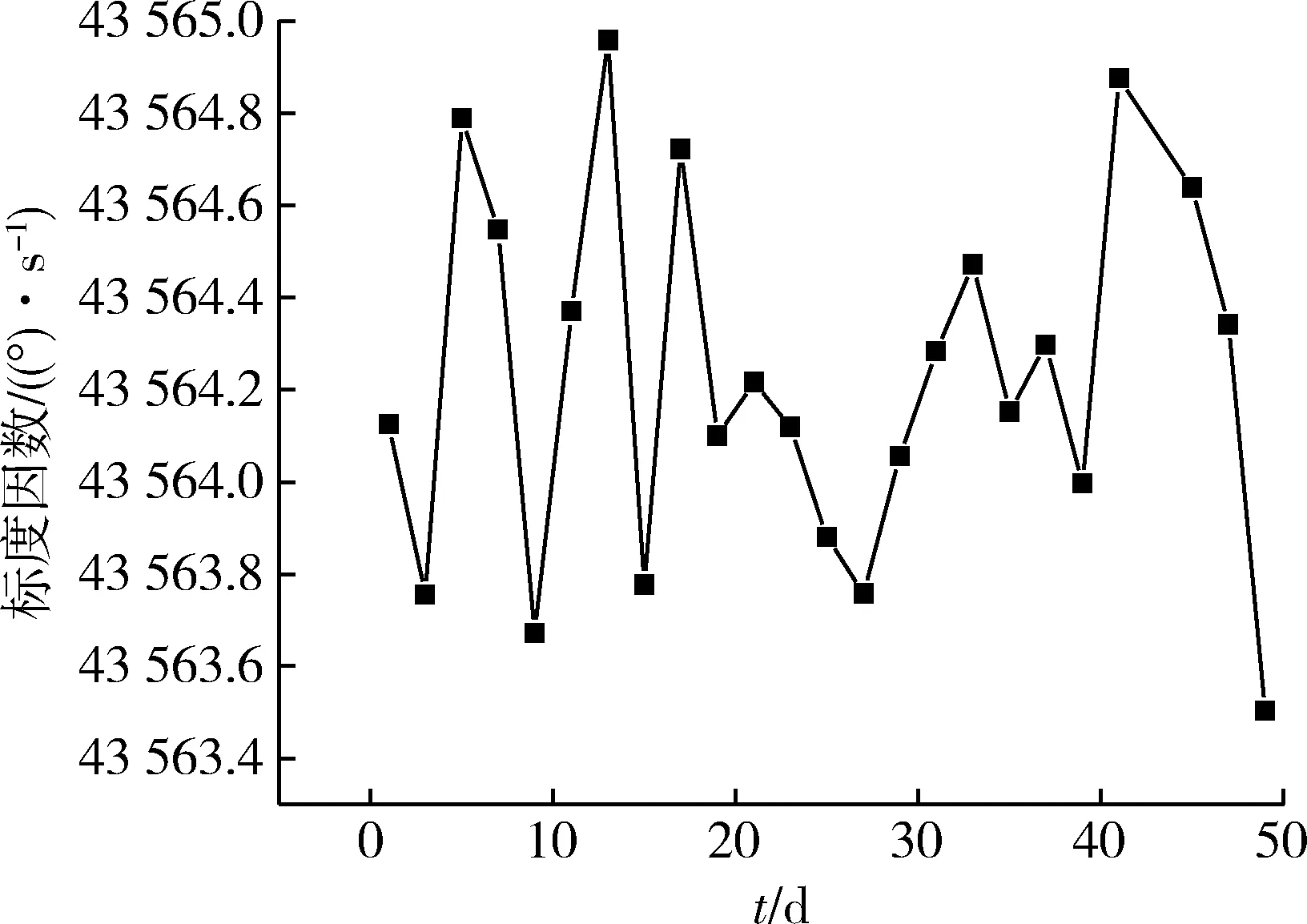
图4 50天重复性测试曲线Fig.4 Curve of scale factor repeatability of gyro

3 大动态陀螺应用

高性能大动态陀螺的出现，改变了传统稳定平台和载体姿态解算的方法。比例导引制导导弹，需要测量弹体视线相对惯性空间的角速度，而导引头本身与弹体固连受其旋转耦合的影响，失去了获取能力。与导引头一起捷联的大动态光纤陀螺能够将弹体本身的视线速率或者角度精确地提供给导引头，保证去耦精度[14-15]。

系统对导引头角度耦合信息的解耦变得简单，通过减去对光纤陀螺角速率积分得到的角度值即可,解耦示意图见图5。但是，与减旋结构的绝对角度位置相比，采用光纤陀螺的纯惯性旋转解耦，仍会存在误差积累的问题，也就是随着工作时间的增加，解耦的效果会渐渐恶化，通过保证陀螺动态精度和稳定性，以及结合多传感器数据融合能够有效改善和提升系统精度。

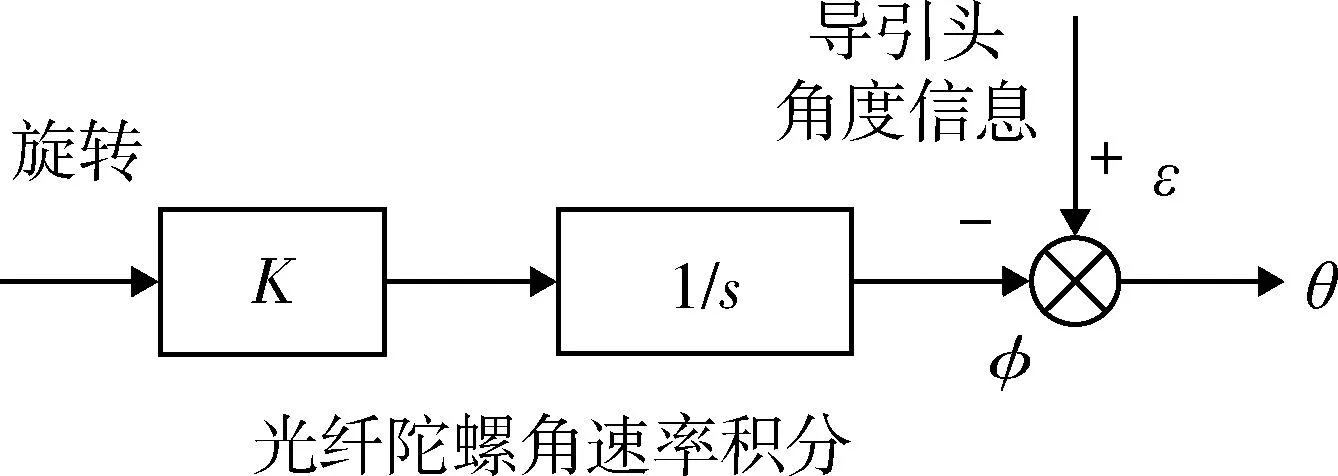
图5 捷联陀螺解耦示意图Fig.5 Illustration of decoupling with strap down gyroscope

4 结束语

对于高速旋转载体中捷联系统的陀螺仪精度和动态范围的需求，本文基于光纤陀螺，提出跨条纹工作实现动态范围的大幅提升，可以保证陀螺精度的基础上，获得大速率范围。通过实验评估，验证了该型陀螺性能的优越性。

[1] HILKERT J M.Inertially Stabilized Platform Technology Concepts and Principles[J].IEEE Control Systems，2008，28(1)：26-46.

[2] KENNEDY P J，KENNEDY R L.Direct Versus Indirect Line of Sight (LOS) Stabilization[J].IEEE Transactions on Control Systems Technology，2003，11(1)：3-15.

[3] 周瑞青，刘新华，史守峡，等.捷联导引头稳定与跟踪技术[M].北京:国防工业出版社，2010.

ZHOU Rui-qing，LIU Xin-hua，SHI Shou-xia，et al.Strap-Down Seeker Stabilization and Tracking Technology[M].Beijing:National Defense Industry Press，2010.

[4] 王晨，董景新，高宗耀，等.火箭弹大动态单轴平台惯导系统姿态算法[J].中国惯性技术学报，2012，20(3)：257-261.

WANG Chen，DONG Jing-xin，GAO Zong-yao，et al.Attitude Algorithm of High Dynamic Range Single-Axis Platform INS on Rocket Projectile[J].Journal of Chinese Inertial Technology，2012，20(3)：257-261.

[5] 王志伟，秦俊奇，狄长春，等.火箭弹载惯导误差分析[J].火力与指挥控制，2016，41(8)：105-108.

WANG Zhi-wei，QIN Jun-qi，DI Chang-chun，et al.Rocket Carrier INS Error Analysis[J].Fire Control & Command Control，2016，41(8)：105-108.

[6] 安亮亮，王良明.高旋火箭弹GPS/SINS组合测姿方法[J].弹道学报，2016，28(1)：39-44.

AN Liang-liang，WANG Liang-ming.GPS /SINS Attitude Measurement Method of High-Spin Rocket[J].Journal of Ballistics，2016，28(1)：39-44.

[7] 祝敬德，李杰，张松,等.半捷联模拟控制减旋电路设计[J].实验室研究与探索，2015，34(6)：46-49.

ZHU Jing-de，LI Jie，ZHANG Song，et al. Semi-Strapdown Analog Control Circuit Design[J].Research and Exploration in Laboratory，2015，34(6)：46-49.

[8] 李玎.基于磁传感器组合的旋转弹体姿态测试方法研究[D].南京:南京理工大学，2009.

LI Ding.Study of Attitude Measurement on Spinning Projectile Based on Magnetic Sensors Unit[D].Nanjing:Nanjing University of Science & Technology，2009.

[9] 李成刚，谢志红，尤晶晶,等.新型无陀螺捷联惯导系统导航方案设计及建模[J].中国惯性技术学报，2015(3)：303-310.

LI Cheng-gang，XIE Zhi-hong，YOU Jing-jing，et al.Gyro-Free SINS Six-Axis Accelerometer Navigation Calculation Basic Inertial Navigation Equation Attitude Update[J].Journal of Chinese Inertial Technology，2015(3)：303-310.

[10] MOSLEHI B，YAHALOM R，OBLEA L，et al.Low-Cost and Compact Fiber-Optic Gyroscope with Long-Term Atability[C]∥Aerospace Conference，2011 IEEE.IEEE，2011：1-9.

[11] CULSHAW B.Optical Fiber Sensor Technologies：Opportunities and Perhaps-Pitfalls[J].Journal of Lightwave Technology，2004，22(1)：39-50.

[12] NAYAK J.Fiber-Optic Gyroscopes：From Design to Production[J].Applied Optics，2011，50(25)：E152-E161.

[13] LEFEVRE H C.The Fiber-Optic Gyroscope[M].Boston:Artech House，2014.

[14] 郭涛，夏群利，祁载康,等.捷联干涉仪导引头旋转弹体角运动解耦设计[J].现代防御技术，2011，39(3)：91-95.

GUO Tao，XIA Qun-li，QI Zai-kang，et al，Decoupling Design of Strapdown Interferometer Seeker with Rolling Body Angular Motion[J].Modern Defence Technology，2011，39(3)：91-95.

[15] 孙高，赵桂军，吕鉴倬,等.半捷联滚仰导引头视线角速度重构提取技术[J].制导与引信，2015，36(2)：10-13.

SUN Gao，ZHAO Gui-jun，LÜ Jian-zhuo，et al.LOS Rate Extraction Technology of Semi-Strapdown Roll-Pitch Seeker[J].Guidance & Fuze，2015，36(2)：10-13.