管梁固定式悬置系统仿真分析及遗传算法优化
2018-01-02周良生
朱 强,周良生
(1.陆军军事交通学院 研究生管理大队;2.军事交通学院运输研究所,天津 300161)
管梁固定式悬置系统仿真分析及遗传算法优化
朱 强1,周良生2
(1.陆军军事交通学院 研究生管理大队;2.军事交通学院运输研究所,天津 300161)
这里介绍一种管梁固定式悬置系统。为了获得管梁固定式悬置系统参数对上装侧倾振动的影响和最优的结构参数,建立了整车多体动力学模型。对上装振动进行仿真分析,并通过遗传算法对管梁式结构参数进行优化。结果显示,管梁固定式悬置系统的扭转刚度参数比位置参数对上装振动的影响程度大。考虑稳定性后,扭转刚度的影响程度也比较大。参数优化后,车辆通过不同路面上装侧倾振动角加速度均有所减小。
管梁;减振;侧倾振动;优化
悬置系统的隔振性能对运输车辆十分重要,它是决定运输车辆效率和寿命的重要因素。管梁固定式悬置系统,对由于路面不平度产生斜对称动载荷给车辆带来的扭转振动能起到明显减弱效果,对上装隔振性能非常好。在悬置系统减振效果进行分析后,需要对悬置系统参数对上装的振动的影响程度进行分析,同时对参数进一步优化。
本文在仿真分析悬置系统的隔振性能后,基于正交试验分析隔振性能对管梁式悬置系统的结构参数的灵敏度。得到各参数对隔振性能的影响程度的不同后,通过遗传算法对悬置系统的参数进行优化,得到最优隔振性能的结构参数,对管梁式悬置系统的进一步深入研究具有比较大的意义。
1 整车多体动力学模型的建立
通过试验获取某运输车辆相关参数,将管梁式柔性体车架通过合理设计安装在整车模型上,获得如图1所示的加装管梁式柔性体车架的整车多体动力学模型。

图1 整车多体动力学模型
2 B级路面仿真分析
在Adams里车辆以60km/h车速在B级随机路面、三角脉冲路面和大扭曲路面进行仿真,通过处理得到其上装质心处侧倾振动角加速度值如表1所示。
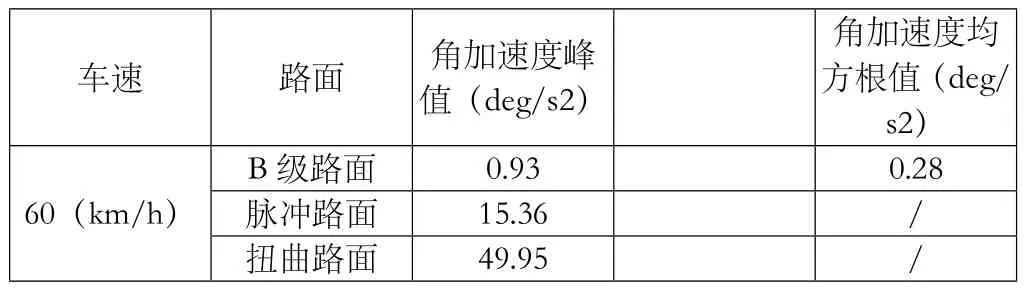
表1 不同路面下上装质心处侧倾振动角加速度
3 利用遗传算法进行管梁固定式悬置系统参数优化
遗传算法是一种模拟自然界生物的遗传法则和自然选择进化论的并行随机搜索的优化方法[4],上个世纪六十年代就由美国人Holland教授提出[5]。主要原理是通过初始化产生种群,种群在进化的过程中进行不断地进行选择、杂交和变异,以获得优良后代的过程。
这里待优化的参数是管梁与车架的固定连接位置X,管梁两端的扭转刚度K1、K2,选取的目标函数为上装质心处侧倾角加速度均方根值(记为R),优化的目的是使得R值最小。
根据悬置结构特性及计算,待优化参数的原始技术参数如表2所示。

表2 待优化参数原始值
优化过程中上装质心处侧倾角加速度均方根值随着迭代数次数的变化如图2所示(横坐标表示迭代次数,纵坐标表示上装质心处侧倾角加速度均方根值)。

图2 上装质心处侧倾角加速度均方根值
由图2可以看出,目标函数随着迭代次数增加时,到第三代之后变化就基本上达到了最小值,再往后基本上不再变化了,算法快速收敛。说明在第三代时待优化参数就达到了最优的取值。经遗传算法优化后管梁与车架的固定连接位置X,管梁两端的扭转刚度K1、K2值如表3。

表3 优化后参数值
经过遗传算法优化后,车辆在通过不同路面时上装质心处侧倾振动角加速度随时间变化曲线与优化前的对比如图3所示。其中红色虚线代表优化后的角加速度随时间变化曲线,黑色实线代表优化前的角加速度随时间变化曲线。

图3 B级路面优化前后上装侧倾振动角加速度随时间变化
优化后,车辆以60km/h车速通过B级路面时,上装质心处侧倾振动角加速度峰值为0.91 deg/s2,均方根值为0.26 deg/s2,分别降低了3.2%和7.1%;遗传算法不仅在悬置系统振动上优化有较好的效果,同时也能通过优化获得更好的参数,对工程实践起到促进作用。
4 结论
(1)以某重型越野运输车为原型,在车架与上装间加装经柔性化处理后的管梁式柔性体悬置结构,通过Adams多体动力学仿真,得到拥有管梁固定式悬置系统的车辆上装侧倾振动的响应变化曲线,结果的精确性比较好。
(2)通过遗传算法对悬置结构参数进行优化,得到优化后目标值除在B级路面外都降低7%以上,效果明显。同时获得了优化后悬置结构的参数值,达到了优化的目的。
[1]王凯楠.运输车辆厢体悬置系统优化设计研究[D].天津大学,2014.
[2]唐天柱.某重型卡车驾驶室振动问题分析及优化[D].湖南大学,2013.
[3]张武,陈剑,陈鸣.采用正交试验的发动机悬置系统灵敏度分析[J].噪声与振动控制,2011,31(05):168-172.
[4]徐利伟.基于改进遗传算法的悬架结构优化[D].河北工程大学,2013.
[5]Nariman-Zadeh N,Salehpour M,Jamali A,et al,Pareto optimization of a five-degree of freedom vehicle vibration model using a multi-objective uniform-diversity genetic algorithm (MUGA),Engineering Applications of Artificial Intelligence,2010,23(04):543-551.
10.16640/j.cnki.37-1222/t.2018.01.002
