运用直观操作构建数学模型

肖雪媛

（晋江市罗山街道荣宗小学，福建 晋江 362216）

运用直观操作构建数学模型

肖雪媛

（晋江市罗山街道荣宗小学，福建 晋江 362216）

《义务教育数学课程标准(2011年版)》强调,数学课堂应重视学生的基本经验的积累和数学思想的渗透，而模型思想又是数学思想的核心思想之一。在教学中，教师应采取有效措施，让学生通过数学活动自己去探索，自己去创造，亲身经历将实际问题抽象成数学模型的过程，进而提升学生的数学素养，培养学生的数学思维。

直观操作；数学概念模型；运算模型；几何公式模型；数量关系模型

2011年版《义务教育数学课程标准》由“双基”变为“四基”。从课程标准的变化看，数学课堂应重视学生的基本经验的积累和数学思想的渗透。因此，课堂上让学生利用典型材料进行动手实践操作，不仅是一种知识和技能的获得，也是对知识产生的一种经历和体验，更是对数学思想的一种感悟，而模型思想又是数学核心思想之一。如何在可操作、可触摸的数学活动过程构建数学模型，发展模型思想呢？

一、运用直观操作，构建概念模型

数学概念是小学数学基础知识的重要内容之一，对于小学生来说，获得精准的概念是一个主动、复杂的过程。由于数学概念的抽象性与小学生思维的形象性是一对矛盾关系。因此，教师要为学生提供丰富而典型的感性材料，让学生通过直观操作、观察分析等实践活动，使抽象的概念具体化，从而正确理解概念，内化概念。教学时，可引导学生进行动手画一画、折一折、分一分、摆一摆、拼一拼等直观操作，为抽象概念的理解打下基础。例如教学“轴对称图形”这一概念时，教师课前为学生准备一些图形卡片，借助对这些图形卡片的分类，找出哪些是轴对称图形？教师追问：“为什么？”然后进行小组讨论，学生经过观察、比较、讨论，对轴对称图形有了初步的感知。教师再次追问：“你们能不能用自己的语言描述什么样的图形是轴对称图形？”学生通过动手操作、观察，最终用自己的语言描述出来，不断丰富和完善轴对称图形的概念的构建。因此在概念教学时，教师可根据概念产生的直观背景设计有效的操作活动，让学生在操作中亲身体验和感悟数学概念的产生和发展过程，促进学生对概念的建构。

二、运用直观操作，构建运算模型

计算教学重在研究在“怎么算”的过程中明白算理，算理本身的抽象性、逻辑性导致数学计算教学枯燥乏味。因此，在计算教学时需结合学生的实际，创造让学生能直接感知的教学情境，通过动手操作实验，帮助学生在轻松愉快的学习氛围中经历计算过程，体验算理，总结算法，构建运算模型。如低年级的运算教学（整数运算）可以让学生利用计数器来拨一拨；中年级的运算教学（小数运算）可以让学生利用百格图来涂一涂；高年级的运算教学（分数运算）可以让学生动手折一折。

师：你能算出结果吗？

借助手中的学具，动手研究，并展示学生的成果：

生1：将一张长方形纸竖着对折两次，取其中的3

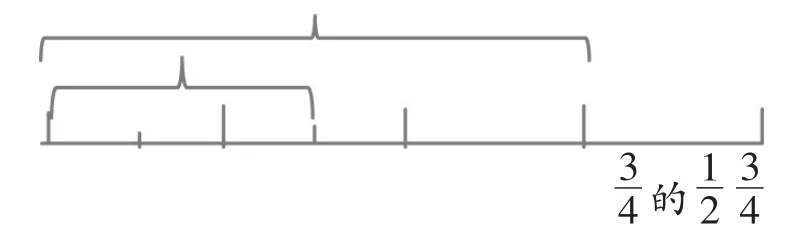
生3：将一个圆形图片平均分成4份，然后将其中的3份再平均分成2份，涂上阴影，也就是3个的。

三、运用直观操作，构建几何公式模型

费赖登塔尔说过：“数学学习是一种活动。”小学生的思维特点是以形象思维为主，逐步向抽象思维过渡。教学中教师应精心设计和组织学生经历实验操作活动过程，让学生自己去拼一拼、摆一摆，仔细观察，详细记录，让学生通过具体操作，思维和语言表达紧密结合起来，在直观操作活动的过程中构建几何公式模型。

例如，长方形的面积计算公式教学，教师为学生准备24个面积为1平方厘米的小正方形学具，请学生摆一摆，摆出不同的长方形并记录，再求出长方形的面积。让学生经历了看似混乱无序的操作过程，学生真实感受到了长方形的面积计算与它的长和宽有关系，从而得出长方形的面积=长×宽。

又如教学“三角形的面积”，课前教师可以为学生准备各种三角形。

师：你可以用什么方法来计算出它们的面积呢？

生1：用格子图数出直角三角形的面积；

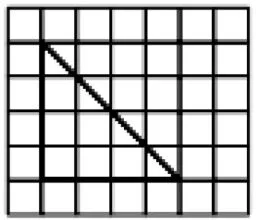
生2：用格子图割补的方法将直角三角形转化成长方形；

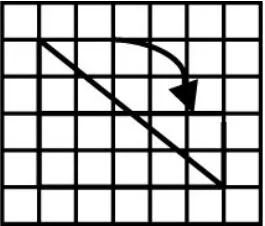
生3：用割补的方法将锐角三角形转化成长方形；

生4：用倍拼法将钝角三角形拼成平行四边形。

大胆放手让学生自主完成对三种不同类型的三角形面积计算公式的主动探索，进而通过深入的分析比较，使学生自然而然地演绎推导出三角形的面积计算公式，从而有效构建几何公式的模型。

四、运用直观操作，构建数量关系模型

数量关系是小学阶段最重要的数学模型之一，可以为学生解决问题提供一些基本的方法。问题解决教学是数学教学的重要组成部分，问题解决的知识又是抽象的，而小学生的思维能力还处于具体形象思维为主的阶段，因此在问题解决教学中，教师要努力为学生搭建探究、发现的学习平台，让学生在直观操作中去探究问题解决的规律。

例如，“小明在一个长25米儿童游泳池里游了4个来回，他一共游了多少米？”小学生对此题的关键句“4个来回”往往难以理解，这时教师可为学生创造一个直观生动的操作平台，让学生把教室的宽当作游泳池的长度，并请一位学生上台表演。当学生从教室一端走到另一端时，教师问：“这是来回吗？”学生自然明白这不是一个来回，只是一个“来”。再让学生返回到原来的位置，又问：“这是来回吗？”这样学生自然能初步理解1个来回是2个25米，再继续追问：“4个来回，应该要走几个25米呢？”然后再让学生2人为一组把课桌的桌面长度看成游泳池的长度来直观操作，进一步理解“一个来回”的意思，再推算出4个来回就是8个25米。又例如，相遇问题中的求“速度和”，学生也是难以理解的，也可以请两位学生进行直观演示。这样的操作将抽象的知识生动化，同时也让学生亲身经历将实际问题抽象成数量关系模型的过程，学生对数量关系的理解更明确，分析问题的能力也得到提升。

学习数学的唯一正确方法是学生再创造，也就是说在教学中，教师应采取有效措施，让学生通过数学活动自己去探索，自己去创造，亲身经历将实际问题抽象成数学模型，这样学生理解了数学模型和它们所表现的数学思想，进而提升学生的数学素养。

［1］教育部.义务教育教学课程标准（2011年版）［S］.北京：北京师范大学出版社，2012.

［2］张海英.数学模型方法及其教学［J］.小学教学教育，2017（5）.

［3］郑毓信.以“深度教学”落实数学核心素养［J］.小学数学教师，2017（9）.

陈志华）