农田表层土壤镉的典型空间插值方法对比研究

张金兰, 欧阳婷萍, 黄铁兰, 喻怀义,刘丽,陈克海



农田表层土壤镉的典型空间插值方法对比研究

张金兰1,*, 欧阳婷萍2, 黄铁兰1, 喻怀义1,刘丽1,陈克海1

1. 广东工贸职业技术学院，广州 510510 2. 中国科学院广州地球化学研究所, 广州 510640

空间插值对于土壤重金属空间分布和污染评价具有重要意义, 以广东省广州市某地区农田表层土壤重金属镉的调查监测结果为例, 选取具有代表性的反距离加权、径向基函数、普通克里金、简单克里金、泛克里金5种空间插值方法, 进行空间插值及土壤等级划分, 比较不同插值方法结果精度, 分析不同插值方法结果差异。研究结果表明: 不同插值方法识别的土壤镉浓度空间分布特征和土壤等级划分存在差异, 主要体现在局部极值向外过渡区域存在较大不确定性, 其中径向基函数精度最高, 克里金插值法对数据存在“压缩”效应较强。因此, 在开展土壤重金属污染调查时应考虑土壤重金属样本数据特征和空间结构特征, 选择合适的插值模型, 并适当加大土壤重金属浓度过渡区域采样密度。

空间插值; 对比研究; 农田表层土壤; 镉

1 前言

我国是耕地资源相对匮乏的国家, 近年来其数量仍在不断减少, 与此同时, 伴随着我国城市化进程推进、工农业生产发展, 人类向土壤中排放污染物质越来越多, 农田土壤环境污染问题越来越突出, 并成为限制农业可持续发展的重大障碍[1-4]。如何全面、准确地掌握区域土壤重金属污染状况, 是防治土壤重金属污染的基础和前提[5-7]。由于土壤异质性以及土壤与重金属间复杂的环境过程, 定量描述土壤重金属空间分布在现有技术上仍存在较大困难[8-11]。目前, 基于地理信息系统(GIS)技术及统计学方法, 通过对离散点数据空间插值进行土壤重金属污染空间识别的技术已取得了较大进展[11]。但是, 目前适用于土壤重金属污染空间插值方法优化的理论尚未形成, 针对不同土壤重金属污染类型的最优空间插值方法仍需要单独研究。

本文以广东省广州市某地区农田表层土壤重金属镉(Cd)为例, 分析5种常用的空间插值方法对镉浓度空间分布识别和土壤等级划分的影响, 通过对比不同插值方法预测误差, 绘制土壤重金属空间分布特征, 对土壤等级进行划分, 对比和分析不同插值方法所得结果, 确定最优插值方法。研究成果可以为区域土壤污染综合防治提供科学依据, 也可以为农产品基地合理规划、优质农产品开发、耕地环境质量保护以及土地可持续利用提供参考。

2 数据来源及方法

2.1 样品采集

本研究区域位于广东省广州市, 面积约为130 km2, 平均气温21.6 ℃, 平均降雨量约为1600 mm, 适宜热带、亚热带作物生长, 是著名的荔枝之乡、鱼米之乡。根据研究区域农田土壤分布, 采用均匀布设原则在整个研究区域内共采集土壤样品93个, 取样深度0—20 cm, 采样时间2013年7—8月份, 图1是研究区域农田土壤以及采样点空间分布情况。采样点用米级GPS定位, 同时记录采样点的土地利用类型及周围环境特征, 采样方法参考《土壤环境监测技术规范》(HJ/T166—2004)。其中有3个样品Cd浓度低于检测线, 将这3个样本点Cd浓度设定为0 mg·kg-1, 根据《国家土壤环境质量标准》(GB156182—1995)Cd二级标准限值(0.3 mg·kg-1), 研究区域pH值均小于6.5, 93个样本中有29个超过二级标准。

2.2 插值方法

目前用于土壤重金属空间插值的方法有很多, 本文采用的是具有代表性的几种插值方法, 有反距离权重法(IDW)、径向基函数法(RBF)、克里金法(Kriging)。

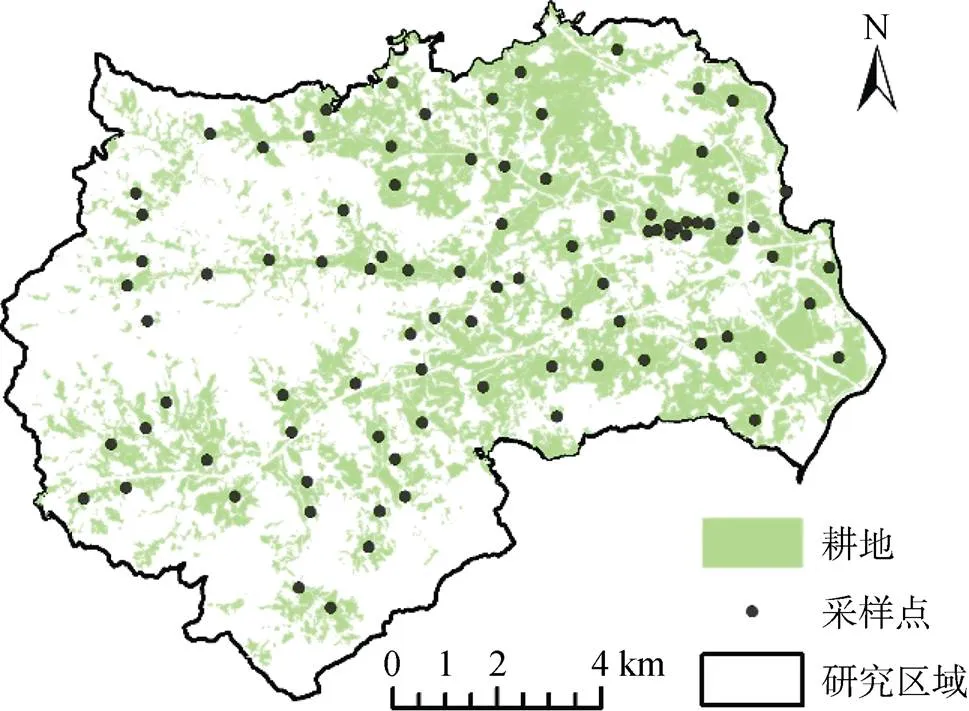
图1 研究区域采样点分布图

(1)反距离权重法(IDW)

反距离权重法(Inverse Distance Weighted, 简称IDW), 是基于距离相似原理, 即距离越近越相似, 考虑空间数据值与距离成相关的空间特性, 其公式为[12,13]

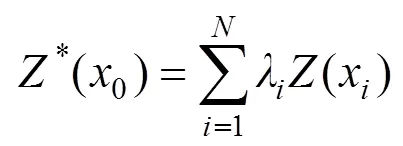
公式(1)中,*(X)为X点处的估值,为用于插值的邻近样点的个数,(X)为样点X处的实测值,λ为第个样点对估值点贡献的权重。

(2)径向基函数法(RBF)

径向基函数法(Radius Basis Function, 简称RBF), 通过基函数计算待估点的一组权系数, 从而实现插值。径向基函数插值法如同将一个软膜插入并经过各个已知样点, 同时又使表面的总曲率最小。径向基函数法与地统计插值方法具有相似性, 它的优点是不需要有关样本数据的任何假设, 但是不具有地统计插值的变差图分析功能。常用的径向基函数有: 规则样条函数、张力样条函数、高次曲面函数、反高次曲面函数、薄板样条函数[12-15]。

(3)克里金插值法(Kriging)

克里金插值法(Kriging)是以空间自相关为基础, 是利用原始数据和半方差函数的结构性, 对区域化变量的未知采样点进行无偏估值的插值方法[3,6]。在满足固有假设的条件下, 其估计公式与IDW的公式相同, 所不同的是其权重系数λ。根据无偏估计和方差最小两项原则来确定加权系数, 其中关键的函数是半方差函数[14]。

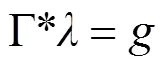
(3)

式中, Γ为所采样点之间对应的半方差函数值组成的矩阵,为权重矩阵,为采样点和预测点对应的半方差函数值组成的向量。γ为第个采样点和第个采样点的权重,为约束预测无偏性变量,γ为第采样点和预测点对应的半方差函数值。将向量乘以Γ的逆矩阵可以求出向量, 根据公式(1)可以求出预测的值。常用的克里金插值法又有普通克里金法(Ordinary Kriging, 简称OK)、简单克里金法(Simple Kriging, 简称SK)、泛克里金法(Universal Kriging, 简称UK)[14]。

2.3 精度评价方法

交叉验证法是一种常见的精度验证方法[3,14,15], 优点在于最大限度的利用观测值, 避免因精度验证需要而减少插值过程的观测数量。常用的交叉验证统计指标主要有平均误差(), 均方根误差(), 可分别表示为:

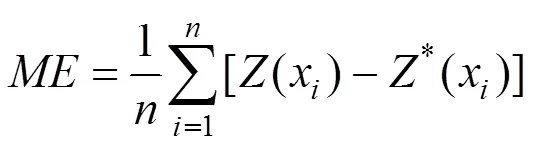
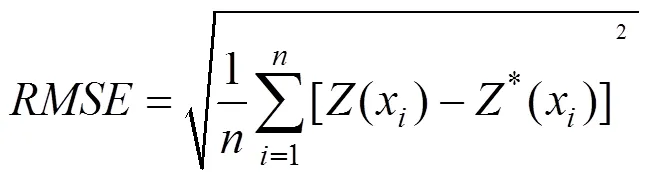
平均误差()是预测无偏的量度, 越接近0说明插值越无偏,是预测精度的量度, 越小越说明插值精度越精确[6]。

2.4 数据处理流程和工具

本文使用ArcGIS10.2软件中Geostatistic Anal­ysis Extension模块对样本数据进行统计分析, 根据克里金插值要求进行异常值处理, 采用GS+9.0进一步分析Cd半变异函数, 确定最优半变异函数。在ArcGIS10.2和Suffer13软件支持下, 针对上述几种空间插值方法, 绘制研究区域土壤Cd浓度空间分布和土壤等级划分, 并进行对比分析。

3 结果与讨论

3.1 土壤Cd统计特征

研究区域农田表层土壤Cd浓度变化范围从0~ 1.89 mg·kg-1, 空间变异系数112.60%, 变异系数大, 峰度系数为27.134, 不成正态分布, 具体见表1。由于异常值对土壤属性空间分布特征干扰较大, 在统计分析时, 变异特别的大样本值甚至对变量的估计有很大的影响; 在土壤重金属空间结构分析中, 异常值会造成土壤重金属空间结构变异増大, 空间相关性减小, 甚至掩盖其固有的空间结构; 在克里金(Kriging)插值时会造成插值连续面中断。因此, 在对变量进行空间结构分析和插值时要对异常值进行处理[16,17]。

参照蔡小冬和钱龙刚异常值处理方法[18,19], 采用阈值法识别特异值, 即样本平均值加减3倍标准差, 在此区间外的数据均定为特异值。当采样数据大于平均值与3倍标准差的和时, 以平均值与3倍标准差的和代替异常值, 反之, 当采样数据小于平均值与3倍标准差的差时, 以平均值与3倍标准差的差值代替异常值。通过异常值处理, 经过对数变换后, 峰度系数为3.361, 基本符合正态分布。

3.2 最优参数确定

插值方法在参数选取不同的情况下会产生不同结果, 故插值方法之间的比较应建立在参数最优前提之下。IDW法和RBF法参数较少, 易于挑选最优参数。本文针对研究区域Cd浓度数据, 采用交叉验证方法进行检验和优选, 确定了IDW法和RBF法最优参数(表2)。

Kriging法参数较为复杂, 主要体现在变异函数拟合上, 经过对变异函数分析拟合, 以决定系数(R)最大和残差()最小为原则选取最佳变异函数模型[3], 最优半方差函数拟合模型及变异参数见表2。

表1 镉数据统计特征值

表2 各插值方法的最佳参数

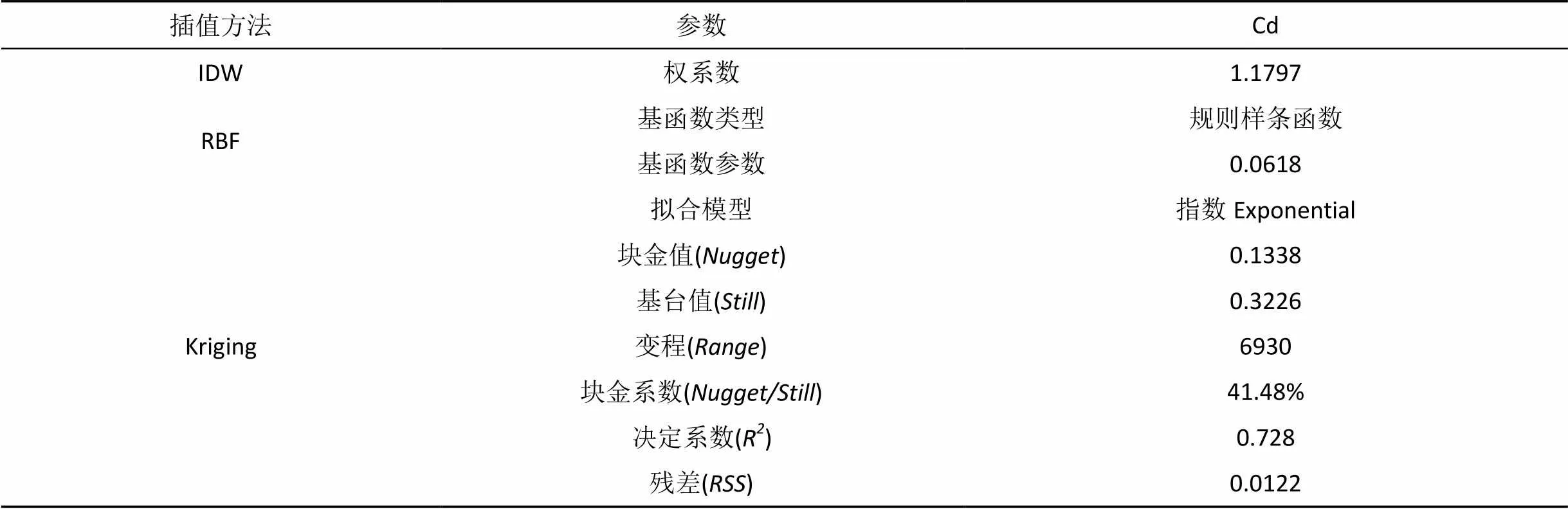
Tab.2 Optimum parameters in interpolations methods

3.3 土壤Cd空间结构特征

在反映区域变量空间变化程度中, 块金系数(块金值与基台值比值)是一个非常重要的指标, 它表明了系统变量的空间相关性程度, 即随机因素造成空间变异性占总变异的比例, 又称为块金效应。通过该比值可以判断影响空间变异的随机因素(人为因素)和结构性因素(自然因素)谁占据了主要作用。块金系数<25%, 说明区域化变量空间变异性以结构性变异为主, 人为因素影响小而受主要受自然因素控制, 各变量之间具有强烈的空间相关性; 25%<块金系数<75%, 表明各变量之间具有程度中等空间相关性; 块金系数>75%, 说明各变量之间的空间相关性比较弱, 以随机性变异为主, 受人为因素影响较大。研究区域Cd块金系数41.48%, 处于25%—75%之间(表1), 属中等相关性, 说明在研究区域土壤镉空间变异既有来自结构性因素(土壤母质、地形等), 又有来自随机因素(灌溉、施肥、耕作措施等)的影响[11,17]。

3.4 不同插值方法的插值精度比较

几种插值方法的交叉验证结果见表3。对比分析可知, kriging法的平均误差较IDW和RBF较大, 三种Kriging方法的平均误差接近。平均误差()最小的是RBF法(-0.0006)。几种插值方法中, 均方根误差()都接近。总体来说, 对于该研究区域土壤Cd浓度最适合的插值方法是RBF, Kriging相对精度较低。

3.5 不同插值方法对Cd污染评价结果比较

5种插值方法下研究区域内Cd空间分布图如图2所示, 几种插值方法预测结果总体趋势上相似, 高值区域集中在研究区域西南部。其中IDW与RBF结果相对更为接近, 三种Kriging方法的结果基本一致, 但与IDW、RBF相比较, 表现出较强的平滑效应, 对数据产生了“压缩”作用, 低值区和高值区且面积较小的区域未能反应出来, 丢失了极大值和极小值信息, 数据比较集中在均值附近。

根据国家土壤环境质量标准(GB15168-1995)对研究区域土壤等级进行划分, 小于0.2mg·kg-1为一级土壤, 0.2—0.3 mg·kg-1为二级土壤, 大于0.3 mg·kg-1为三级土壤[20], 研究区域土壤等级划分空间分布如图3所示, 具体不同等级土壤比例如表4所示。

可以明显地看出, 不同插值方法对土壤等级划分结果不一致, 三种Kriging插值法结果基本一致, 其中OK和UK对土壤等级划分没有区别。Kriging对一级土壤估算面积最大, 比例为30%左右, 对三级土壤估算面积最小, 所占全区比值为24%左右。IDW一级土壤比例最低, 仅为11.9%, RBF三级土壤比例最高, 占32.5%, 比OK和UK高出接近10%。

表3 插值交叉验证误差统计结果

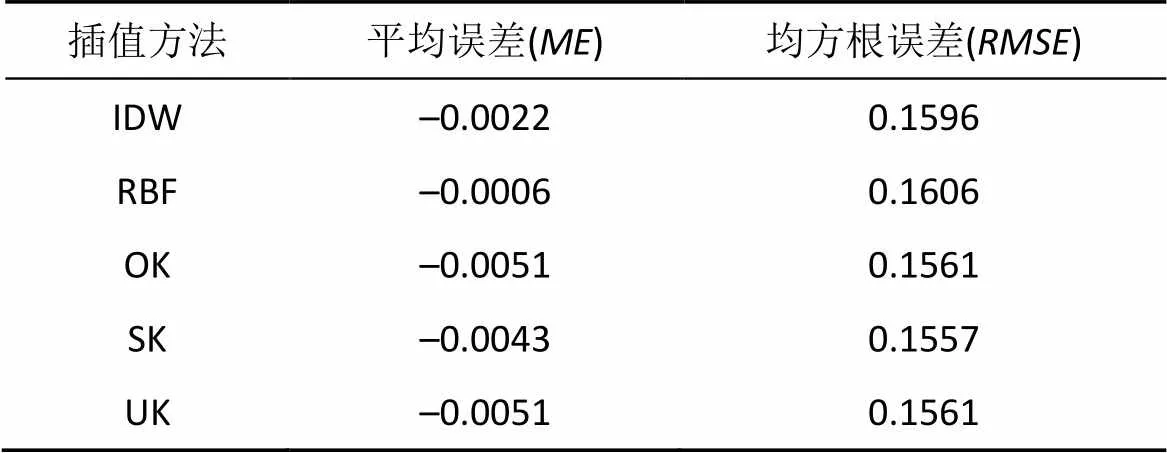
Tab.3 Error statistics of interpolation cross validation

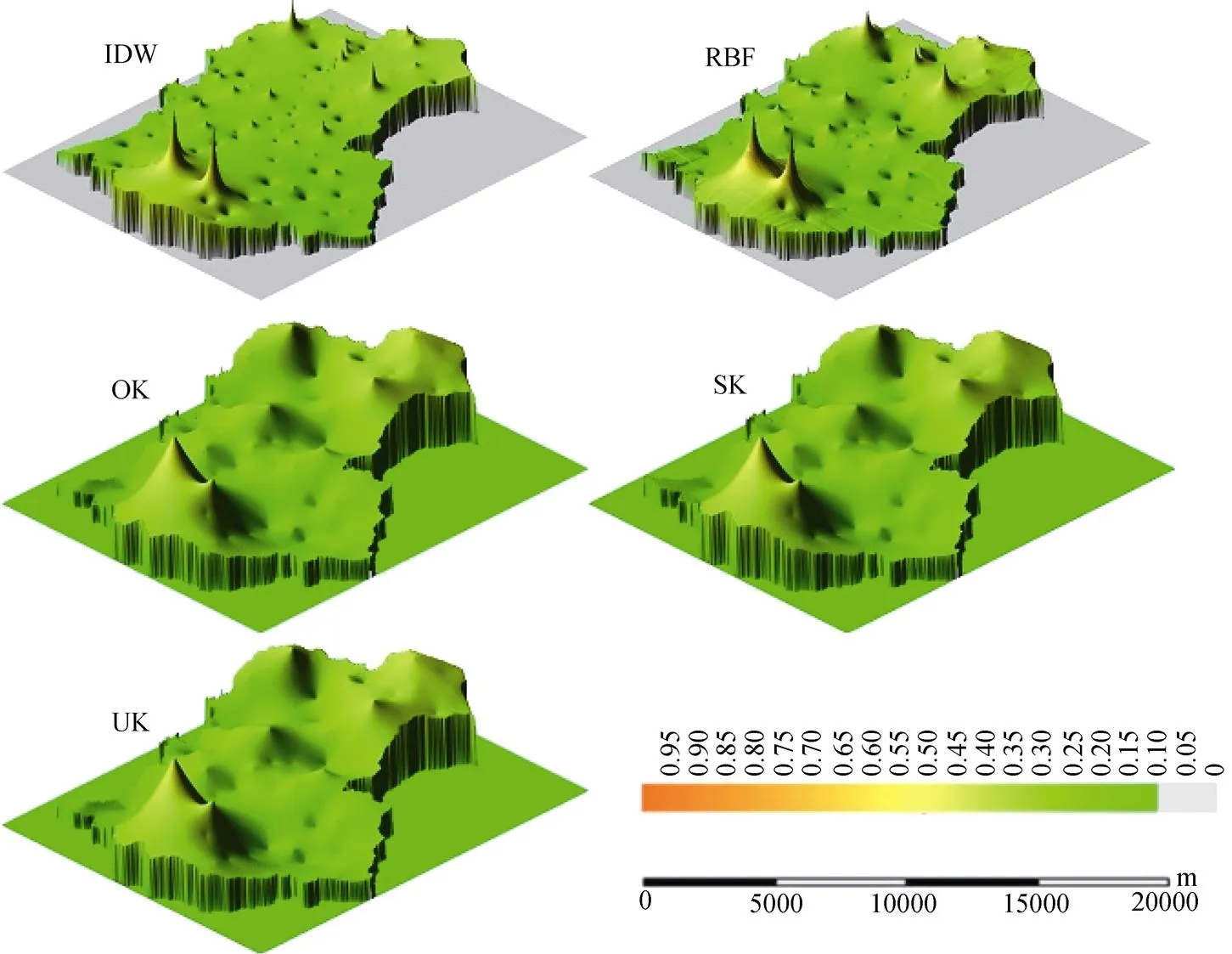
图2 不同插值方法镉的空间分布

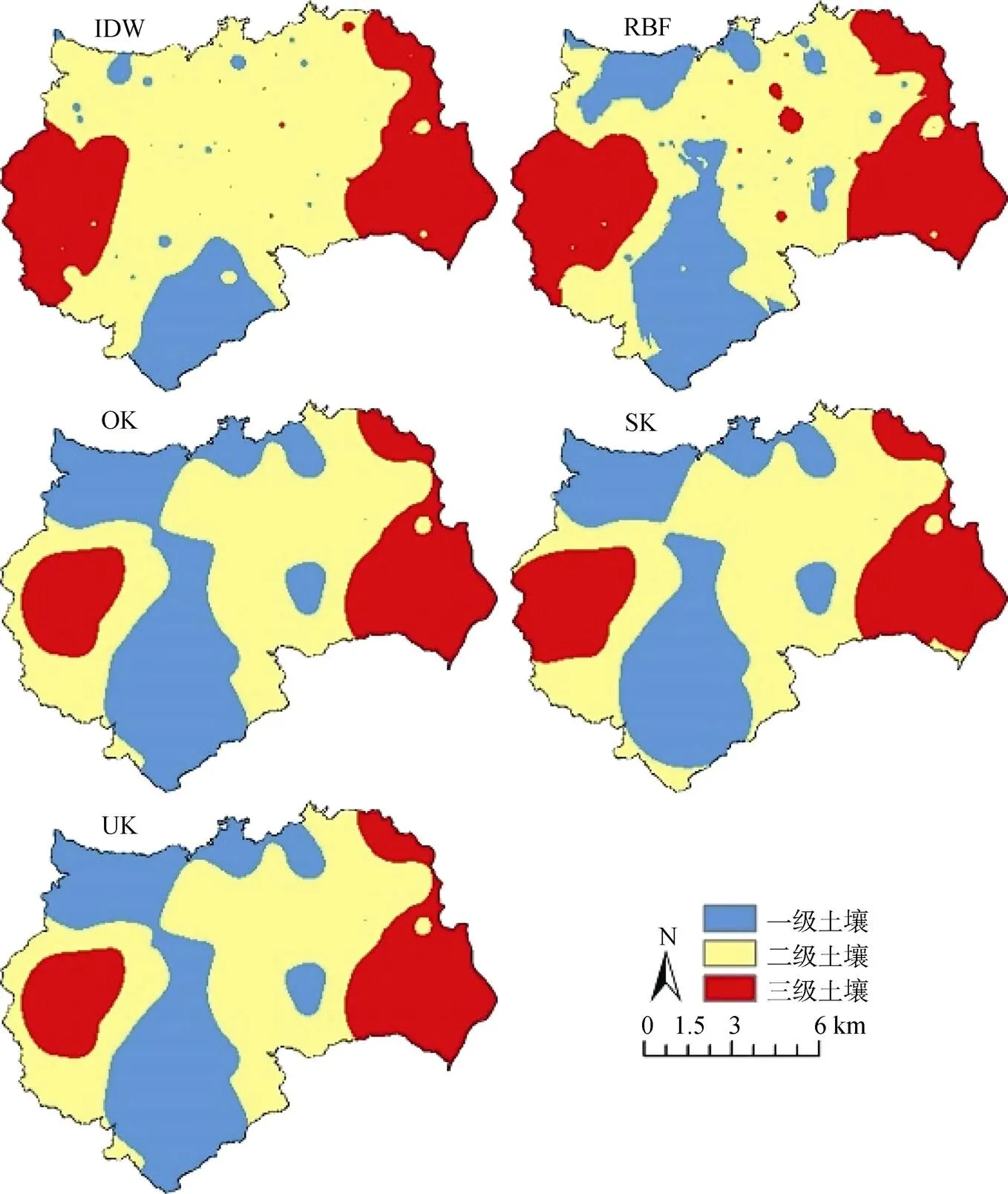
图3 不同插值方法下土壤等级评价

表4 不同插值方法重金属Cd各土壤等级所占比例(%)

空间分布上, IDW和RBF对土壤等级划分比较离散, 结果差异主要体现在: 局部极大值区域和极小值区域, 在高浓度向低浓度过渡区域内或低浓度向高浓度过渡区域, 不同插值方法土壤等级划分边界范围存在较大不确定性。

4 结论

本文从最优参数确定、插值精度等方面比较了IDW、RBF和三种不同克里金插值方法对研究区域内土壤Cd污染格局识别的影响, 得出以下结论:

(1) 基于交叉验证精度评价方法, 对研究区域土壤Cd浓度插值预测, RBF方法和IDW方法优于克里金插值方法, RBF精度最高。

(2) 几种插值方法对研究区域土壤Cd浓度空间分布预测结果总体趋势一致, 浓度较高区域集中在研究区域西南部和东北部。其中克里金方法表现出较强的平滑效应, 丢失了极值信息, 不利于研究区域土壤Cd浓度局部突变特征的展示。

(3) OK和UK所识别的研究区土壤Cd等级划分一致, 其他3种方法均存在差异, 主要体现在局部极值向周边过渡区域, 在过渡区域存较大不确定性。

综上所述, 在进行土壤重金属污染调查过程中, 应当适当加大过渡区采样点密度, 考虑样本点数据特征和空间结构特征, 选择合适空间插值模型, 以提高土壤重金属浓度评估与土壤等级划分精度。

[1] GAO Zhiqun, FU Weijun, ZHANG Meijian, et al. Potentially hazardous metals contamination in soil-rice system and it’s spatial variation in Shengzhou city, China[J]. 2016(167): 62–69.

[2] CHEN Tao, CHANG Qingrui, LIU Jing, et al. Identification of soil heavy metal sources and improvement in spatial mapping based on soil spectral information: A case study in northwest China[J]. 2016(565): 155–164.

[3] 陈思萱, 邹滨, 汤景文. 空间插值方法对土壤重金属污染格局识别的影响[J]. 测绘科学, 2015, 40(1): 63–67.

[4] 李瑞平, 姜咏栋, 李光德, 等. 基于GIS的农田土壤重金属空间分布研究[J]. 山东农业大学学报(自然科学版), 2012, 43(2): 232–238.

[5] 李东升. 施昆, 毕廷涛, 等. 基于GIS的云南省会泽县海镇土壤中重金属插值方法[J]. 科学技术与工程, 2011, 11(10): 2282–2285.

[6] 付传城, 王文勇, 潘剑君, 等. 南京市溧水区土壤重金属污染不同插值方法的对比研究[J]. 土壤通报, 2014, 45(6): 1325–1333.

[7] XIE Yunfeng, CHEN Tongbin, LEI Mei, et al. Spatial distribution of soil heavy metal pollution estimated by different interpolation methods: Accuracy and uncertainty analysis[J]. Chemosphere, 2011(82): 468–476.

[8] 尤冬梅. 农田土壤重金属污染监测及其空间估值方法研究[D]. 北京, 中国农业大学, 2014.

[9] 黄勇, 郭庆荣, 任海, 等. 地统计学在土壤重金属研究中的应用展望[J]. 生态环境, 2004, 13(4): 681–684.

[10] LIN Yupin, CHANG Tsunkuo, TENG Tungo. Characterization of soil lead by comparing sequential Gaussian simulation, simulated annealing simulation and kriging methods[J]. Environmental Geology, 2001(41): 189–199.

[11] 钱翌, 于洪, 王灵. 乌鲁木齐市米东区农田土壤重金属含量的空间分布特征[J]. 干旱区地理, 2013, 36(2): 303– 310.

[12] 李湘凌, 张颖慧, 杨善谋, 等. 合肥义城地区土壤重金属污染评价中典型插值方法的对比[J]. 吉林大学学报(地球科学版), 2011, 41(1): 222–227.

[13] 袁峰, 白晓宇, 周涛发, 等. 元素空间分布插值方法的对比研究: 以铜陵地区土壤中的重金属元素为例[J]. 地学前缘, 2008: 15(5): 103–109.

[14] SUN Yue, kANG Shaozhong, LI Fusheng, et al. Comparison of interpolation methods for depth to groundwater and its temporal and spatial variations in the Minqin oasis of northwest China[J]. Environmental Modelling& Software, 2009(24): 1163–1170.

[15] XIE Yunfeng, CHEN Tongbin, LEI Mei, et. Spatial distribution of soil heavy metal metal pollution estimated by different interpolation methods: Accuracy and uncer­tainty analysis[J]. Chemosphere, 2011(82): 468–476.

[16] 郭旻欣, 喻根, 王晓辉, 等. 基于GIS的淮南市土壤Cu含量克里格插值方法比较研究[J]. 湖北农业科学, 2015, 54(20): 4993–4998.

[17] 余云龙. 基于GIS的海南岛土壤重金属含量空间分布与污染评价[D]. 海口:海南师范大学, 2014.

[18] 蔡小冬. 白银市白银区耕地耕层土壤重金属污染空间分异与环境污染评价研究[D]. 兰州:甘肃农业大学, 2014.

[19] 钱龙刚. 基于GIS的福临农庄土壤重金属空间分布研究和生态风险评价[D]. 扬州:扬州大学, 2014.

[20] 国家环境保护局. GB15618—1995, 土壤环境质量标准[S]. 北京: 中国标准出版社, 1995: 84–86.

张金兰, 欧阳婷萍, 黄铁兰, 等. 农田表层土壤镉的典型空间插值方法对比研究[J]. 生态科学, 2017, 36(6): 130-136.

ZHANG Jinlan, OUYANG Tingping, HUANG Tielan, et al. Comparison of typical interpolation methods for spatial distribution of Cd in soil[J]. Ecological Science, 2017, 36(6): 130-136.

Comparison of typical interpolation methods for spatial distribution of Cd in soil

ZHANG Jinlan1,*, OUYANG Tingping2, HUANG Tielan1, YU Huaiyi1,LIU Li1, CHEN Kehai1

1. Guangdong Polytechnic of Industry and Commerce, Guangzhou510510, China 2.Guangzhou Institute of Geochemistry, Chinese Academy of Sciences, Guangzhou 510640, China

Spatial interpolation played an important role in spatial distribution of heavy metals in soil and pollution assessment. The spatial distribution of Cd and rank of soil on the surface of a region in Guangdong province was studied by five typical spatial interpolation methods, including Inverse Distance Weighted, Radial Basis Functions, Ordinary Kriging, Simple Kriging and Universal Kriging. The accuracy and spatial distribution of different interpolation methods were tested and compared. The results showed that Radial Basis Functions performed best. The spatial distributions of Cd concentration and rank of soil identified by five methods were different. Especially, the uncertainty of the interpolation results among the methods were mainly located in the transitional region around of extreme concentration. The result of Cd concentration by Krigingmethodwascompressed more intensity than other interpolation methods. Therefore, the size and attribute characteristics of sample dataset should be considered in the selection of spatial interpolation method when surveying the soil heavy metal pollution. Meanwhile, the sampling density in the transitional region should be increased to improve the interpolation accuracy.

spatial interpolation; comparative study; farmland soil on the surface; Cd

10.14108/j.cnki.1008-8873.2017.06.018

X53

A

1008-8873(2017)06-130-07

2016-10-21;

2016-12-30

广东工贸职业技术学院科研青年项目(2015-Z-04); 国家自然科学基金委员会广东联合基金项目(U1201131); 国家自然科学基金项目(41272384)

张金兰(1984—), 女, 江西人, 硕士, 讲师, 主要从事遥感与地理信息系统应用研究, E-mail: lanlan1120@126.com

张金兰