基于有效体验下的数学概念教学
2017-12-28胡海光
胡海光
【摘要】体验既是刻画数学活动水平的过程性目标动词,也是学生学习数学的一种很重要的方式,通过创设有效体验,促进学生的数学思考,把数学学习过程变成学生乐于参与、乐于接受、乐于创造的过程是值得我们广大一线教师思考的问题。
【关键词】体验;数学思考;概念教学
体验即“以身体之,以心验之”,简单地说,就是人对万事万物的亲身经历而印象深刻的心灵感悟。《数学课程标准》对体验做了这样的界定:参与特定的数学活动,主动认识或验证对象的特征,获得一些经验。体验既是刻画数学活动水平的过程性目标动词,也是学生学习数学的一种很重要的方式。现代教育理论认为:“最有效的学习是学生对学习过程的体验,它能给学生自主构建知识和情感体验的空间,激发学生的思维。”“课程不再只是文本课程,更是被教师与学生实实在在感受到、领悟到、思考到的体验课程。”因此,如何通过创设有效体验,促进学生的数学思考,把数学学习过程变成学生乐于参与、乐于接受、乐于创造的过程是值得我们广大一线教师思考的问题。下面笔者就以《角的度量》一课为例,谈谈对此的看法。
一、结合已有经验,有效体验概念产生过程
经验是体验的基础。离开了经验的学习,就不是真正的体验学习。教育心理学研究也表明:“当学生学习的材料与已有的经验挂钩时,学生对学习才会充满兴趣。”因此,教师要从学生的“已有经验”出发,结合学习素材,设计引发知识迁移和激发探索心向的导向性问题,从而建立起学生已有知识经验与新知识的联系,使数学概念产生的过程变为真实的、现实的体验。
人教版四年级《角的度量》是这样编排的:用角的大小比较引发角度测量需求,进而认识角的测量单位、测量工具及测量方法。但在实际教学中,按照教材这样设计,学生很难体验角的测量单位产生过程及其含义,教师在实际教学中,常一笔带过角的度量单位的产生过程与认识,把大量的时间用来认识量角器与量角操作,使数学课堂中只有操作,而缺乏深度的体验与数学思考。如何让学生自然而深入地体验角的测量单位产生过程及其意义呢?
【片断1】
1.电脑演示:从一点出发引出N条射线.
观察,你想说些什么?(从一点出发可引出无数条射线;构起了很多个小角等)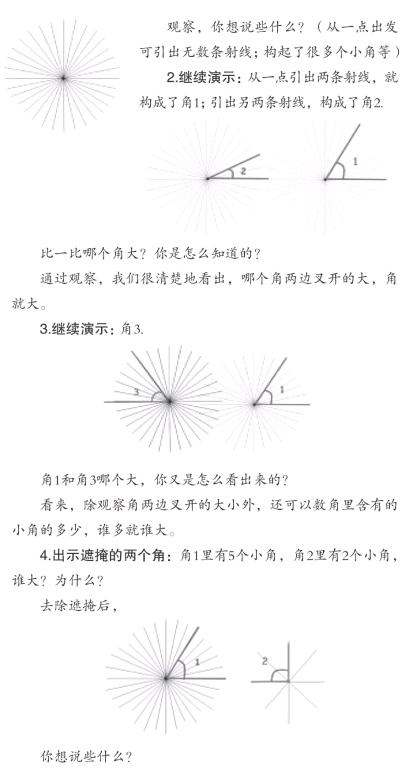
2.继续演示:从一点引出两条射线,就构成了角1;引出另两条射线,构成了角2.
比一比哪个角大?你是怎么知道的?
通过观察,我们很清楚地看出,哪个角两边叉开的大,角就大。
3.继续演示:角3.
角1和角3哪个大,你又是怎么看出来的?
看来,除观察角两边叉开的大小外,还可以数角里含有的小角的多少,谁多就谁大。
4.出示遮掩的两个角:角1里有5个小角,角2里有2个小角,谁大?为什么?
去除遮掩后,
你想说些什么?
▲小结:看来用小角比角的大小,需要统一大小才行。
如果比较这两个角,用哪个角作标准比较好?如果比较更小的角呢?
看来,要准确地比出角的大小,我们不仅要有统一的小角,这个小角的大小还要适度。
《角的度量》是一堂测量课,它与长度的测量、面积的测量无论在结构上、教学方式上都有着或多或少、或明或暗的联系,学生在学习长度的测量、面积的测量中或多或少地积累了学习测量单位及测量方法的经验。这些联系、结构、经验,能够更有效地促进学生对于测量单位度的认识与理解,能更深刻地体验角度单位的形成过程与方法。片断1中,教师充分借助了学生学习长度单位、面积单位的学习经验与活动模式,创设了有小角背景的角的大小比较,让学生自主体验到角的大小比较,不仅可以直观地比较两边叉开的大小,更可以借助于背景小角的数量来比较,进而在小角数量相同但单位小角不同的角的比较情景中,让学生水到渠成地体验到角度测量需要统一单位。
二、遵循认知规律,有效体验概念本质属性
遵循學生的认知规律是体验的前提。对小学生而言,由于年龄较小,缺乏足够的感性材料和实际生活经验,抽象逻辑思维能力、语言理解能力等较差,他们的认知水平基本上停留在感知、动作、表象的水平。因此,教师要遵循学生的实际认知水平,按照知识形成的规律设计教学,从而使数学概念本质属性揭示的过程成为学生自然体验的过程。
【片断2】
1.认识1度
(1)出示关于1度角的规定。让学生读一读。
(2)用手势比一比1度角的大小,说一说对1度角的感受。
(3)在圆形纸上找一找1度角,可以找到几个1度角?
▲小结:每两个刻度线之间所对的角度就是1度,这个圆上共可以找到360个1度。
2.认识几度
(1)认识10度。出示圆上的其中一个10度角,让学生说角度。可以找到几个10度?
(2)学生活动:在圆形图上自己画一个角,并说出这个角的度数。
汇报:选择2至3名学生上台交流,说说这个角是几度,为什么?如果我要找一个5度角,可以怎么找?
(3)深化:要知道一个角的度数,我们只要怎么办就行了?(弄清楚这个角里有几个1度的小角,就是几度了。)
如果角比较大,也是1度1度地数吗?(可以先数几个10度,再数几个1度)
3.小结回顾:看来,一个角有多大,我们只要知道这个角里含有多少个1度的角。
角的度量的本质是角的度量单位的累加。要真正让学生掌握角的度量,就需要让学生真正理解什么是角的度量。在片断2中,让学生经历了从1度到10度再到几度的认识过程,并在这个过程中,让学生通过观察、动手操作、表达、反思,深刻地体验角的度数本质是一个角里含有几个1度角。这些从一到多、逐层深入的体验,让学生真正理解角的度量这个概念的本质,使后续的用量角器量角不再是机械的操作。
三、设计铺垫问题,有效体验概念外延特征
设计铺垫式的问题是有效体验的关键。概念的外延是指具有概念所反映的本质属性的对象。只有把握了概念的内涵与外延,我们才能说理解了这个概念,才能真正融会贯通地应用这个概念。设计铺垫式的问题,通过由浅入深、由易到难,抽丝剥茧式的层层分析,让学生充分体验概念外延的展现过程。
【片断3】
1.看图说度数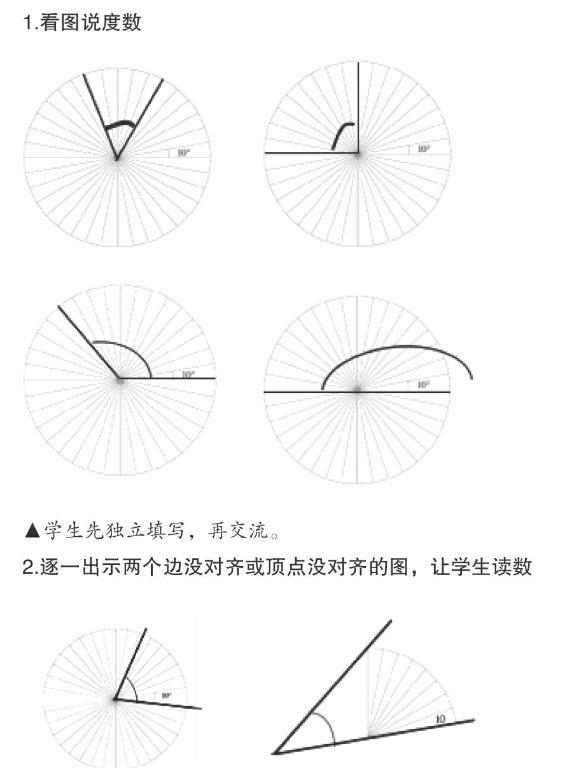
▲学生先独立填写,再交流。
2.逐一出示两个边没对齐或顶点没对齐的图,让学生读数
▲为什么你们不能像刚才那样快速地读出角1的角度?(因为这个角的边没有刚好与圆形图的线对齐,不好数出角度)
▲那么让你来重新放置圆形图,你会注意些什么?(把圆形图的线与角的一条边对齐,这样就比较容易读出角的度数)
▲角2为什么不是80度,这里不是含有8个10度小角吗?(因为小角的顶点没有与角2对齐,所以这些小角不是角2的)
反思:回顾刚才的活动,怎样放圆形小角图,才能又快又对地读出角的度数?
▲相机板书: 线-------边 重合
点-------點
3.估一估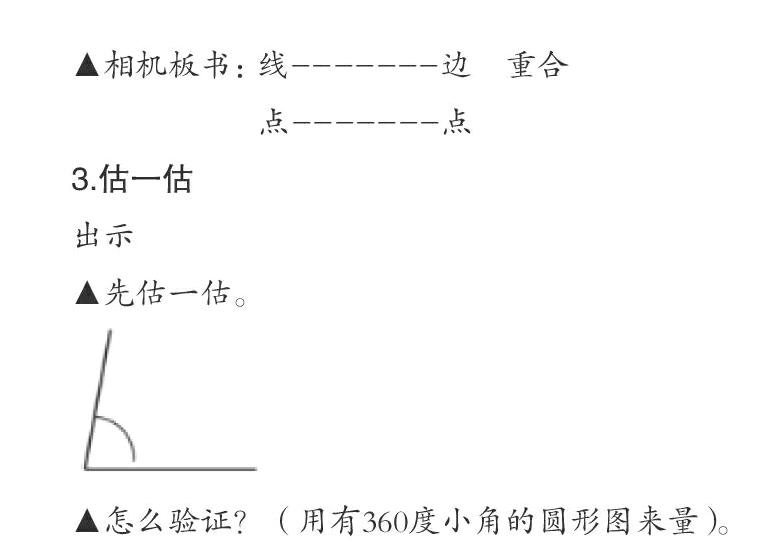
出示
▲先估一估。
▲怎么验证?(用有360度小角的圆形图来量)。
片断3中,通过让学生经历正例、变式、反例等各种情况角度的读数,在肯定例证与否定例证的辨析中,进一步理解角的度量的本质。在这多层次、多维度的练习活动中,也让学生自主感悟、体验到角的度量的外延:在“线边重合、点点重合”前提下的所含有的单位角度的个数。厘清了概念外延,也就为概念的应用做好了准备。
四、开展小组合作,有效体验概念实际应用
小组合作使学习个体之间的互补性得到充分发挥,合作能力、思维能力,创新意识得到整体发展,它是有效体验的生长点。体验学习不仅仅是一种个人学习行为,更应该是一个开放对话的过程。与伙伴讨论交流,发表各自的观点,听取别人的意见,从而使概念应用的过程成为思维碰撞、共享成功、共享智慧的协作体验过程。
【片断4】
1.出示量角器
▲观察并思考:
A:量角器与我们刚才研究的圆形图有什么相同之处?
B:量角器上的这些数是什么意思?
C: 怎样用量角器量角?
同桌商量。
2.汇报交流
▲相机教学量角器的中心点、0度刻度线。
▲先尝试量角1。
▲反馈交流,规范量角方法。
线-------边 点-------点 重合
▲再量角2,量后一生投影反馈,其他核对。
▲小结:量角的时候要注意什么?
用量角器量角的实质是角的度量概念的应用。清晰理解角的度量的概念,并不意味着学生借助这些理解就能正确、熟练地应用量角器来量角度了。片断4中,教师通过创设有要求的活动,让学生通过自主观察比较量角器与圆形图的差异,沟通圆形图的联系,然后尝试量角,使学生体验到用量角器量角实质上是角的度量的概念的应用,然后自主学会量角的方法。
综上所述,概念教学不能仅停留在直观的操作上,而是要用学生的有效体验架起理性思考与实践活动的桥梁,使学生的数学概念学习过程成为一种自我构建的过程。
【参考文献】
[1]杨四耕.什么是“体验”:一个教育学概念的研究[J].今日教育,2009(5):34-37.
[2]林修英.关注概念的形成过程——以《认识几分之一》教学为例[J].福建教育:小学版,2012(7):113-114.
