基于KiK-net强震记录场地放大系数的深度校正因子估计及应用

卞方东，丁海平

（苏州科技大学 江苏省结构工程重点实验室，江苏 苏州 215011）

基于KiK-net强震记录场地放大系数的深度校正因子估计及应用

卞方东，丁海平

（苏州科技大学 江苏省结构工程重点实验室，江苏 苏州 215011）

日本KiK-net强地震动观测台网记录了大量的地表和钻孔下基岩加速度记录，这为分析场地地震效应提供了基础。为保证统计结果的合理性，对震级、震中距及震源距进行了选择，筛选出102个台站1 233组数据记录。利用这些地震记录，采用Cadet提出的场地放大系数的校正因子方法，计算、拟合了基于土层深度的放大系数校正曲线函数，并根据得到的场地放大系数的校正因子，计算了场地影响系数Fa，给出了不同场地影响系数的建议值。结果表明，深度校正因子的估计对基于中国场地分类的场地调整系数有着潜在的研究价值。

KiK-net强震记录；放大系数；校正因子；场地影响系数

场地放大系数对建筑结构抗震设计有着重要影响，在第五代 《中国地震动区划图》（GB 18306-2015）[1]中，增加了考虑场地影响的场地地震动峰值加速度调整系数，《建筑抗震设计规范》（GB 50011-2010）进行局部修订，编制成的《建筑抗震设计规范》（GB 50011-2010）（2016年版）[2]也反映这一结果。一般地，研究场地放大系数最常用的方法——标准谱比法（SSR）[3-8]，即利用土层场地和附近参考基岩场地的强震记录的谱比获得。这一方法存在的问题和困难在于：真正的基岩场地很难找到，因为基岩表面的风化层普遍存在[9]，而非常靠近土层场地的参考基岩场地（都有强震记录）很少。对于国内研究者，还由于国内强震数据的匮乏，常常采用国外地震记录分别进行不同土层类别的地表峰值加速度衰减模型拟合，从而各类场地的放大系数[10]，或计算各类场地的EPA（或PGA），将Ⅱ类场地的EPA（或PGA）作为地震动强度分档指标，将各类场地的EPA（或PGA）均值除以Ⅱ类场地EPA（或PGA）均值，得出场地调整系数[11-13]。由于强震动记录受场地条件影响很大，以及收集资料的代表性和广泛性受到限制，人们利用理论方法和数值模拟手段为场地条件对地震动影响的研究进行了补充[14-16]。

日本KiK-net台阵[17]是含有700多个台站的强地震动观测台网，平均每20 km就有一个台站并覆盖日本。在台站的地表和孔下基岩都各有一对三分量（E-W，N-S，U-D）加速度强震仪。自运行以来，记录了大量强震数据，这给研究土层对基岩的地震动放大效应带来了方便。但由于所有记录位置（台站）并没有公共的露头基岩参考站，传统的SSR不能直接应用于KiK台阵覆盖的区域而获得放大因子。文献[18-19]通过对所有数据进行广义反演获得了放大因子，但反演需要考虑震源、传播途径和各个站点场地等因素，结果并不理想。文献[20-21]则直接利用每个钻孔中地表和基岩记录的比值，得到不同类型场地的放大系数，但由于每个钻孔基岩的深度和各层土介质的波速等参数存在差异，而且也没有考虑地震波在土介质之间的反射影响，得到的结果存在精度问题。为了减小这些影响并提高精度，人们提出了很多改进方法[22-23]。文献[23]亦是以日本KiK-net台阵为基础，利用井下基岩参考谱比法BSR（地表地震动与井下基岩地震动的傅里叶谱比）计算场地放大系数，因上述因素，井下基岩参考谱比法（BSR）与标准参考基岩谱比法SSR（地表地震动与露头基岩地震动的傅里叶谱比）得到的场地放大系数之间存在偏差。文献[23]提出了一个对BSR进行校正的方法，得到的校正因子可以使井下基岩参考谱比法（BSR）与标准参考谱比法（SSR）计算结果比较接近。

文中对KiK-net台阵的强震数据进行合理选取，利用文献[23]的方法进行了校正因子拟合，并给出了不同场地类别的场地调整系数的统计。

1 地震记录的选取

采用的强震数据来自于日本KiK-net强震动观测台网2000年1月1日到2015年12月30日内102个台站1 233组记录，每组数据包括地表及井下的东西、南北、竖向三分量6个记录。地震动的影响参数很多，为了保证数据的合理性，其筛选条件为：①震级高于4.5级；②震源深度小于50 km；③震中距小于100 km。

2 场地校正因子及其拟合

2.1 场地校正因子

参考场地A为土层地表，B为孔底，C位于假定的很深（8 km）的硬基岩处（剪切波速Vs=3 600 m/s），D为假定地表基岩（该基岩满足剪切波速Vs30=800 m/s，卓越频率f0≥8 Hz），如图1所示。这些点的傅里叶谱比SSR=A/D称为标准谱比，BSR=A/B称为井下基岩谱比。理想的SSR可直接利用地表地震动与附近参考基岩场地地震动得到，但并不是所有的KiK-net地震台站都拥有附近参考基岩场地，在KiK-net地震台站都同时拥有地表地震动和井下基岩地震动，可以得到BSR。由于KiK-net各台站的井下基岩深度（通常在100～300 m）、孔底介质波速（VSDH=300～3 300 m/s）差异很大，这大大影响了地震波在台站土介质中的传播，从而导致各台站的BSR与SSR不相等，而场地校正因子的提出是为了使BSR更接近于SSR，从而利用井下基岩谱比BSR代替传统的标准谱比法SSR，具体可参考文献[23]，主要步骤如下。

首先利用日本KiK-net竖向钻孔记录GIFH09（11个真实地震动）和一个假定的场地模型（土层的剪切波速为800 m/s，在1 500 m下的基岩剪切波速2 000 km/s），并以钻孔底部基岩记录作为输入，采用线性化的方法进行土层地震响应模拟，计算不同深度土层（40、80、160、320 m）的地震动及相应深度的加速度反应谱Rsurf，定义钻孔底部基岩加速度反应谱为RDH，得到反应谱比Rsurf/RDH，如图2所示（11条谱比的平均值）。反应谱比 Rsurf/RDH的第一个峰值对应于各自的共振频率 f0，分别为 5、2.5、1.25、0.625 Hz。从图2看出，低频时谱比接近1和谱比幅值从略低于各自的共振频率时开始增加。曲线的值在共振频率时达到最大值，最大值约为3.5，这主要与共振频率有关。对于频率高于3f0的反应谱比（称之为平均校正因子）稳定在1.8。从中可以得出，井下台站的深度会对地震动的放大产生不同的影响，这就需要对深度作一个校正。

图1 土层场地地表与井下基岩模型图

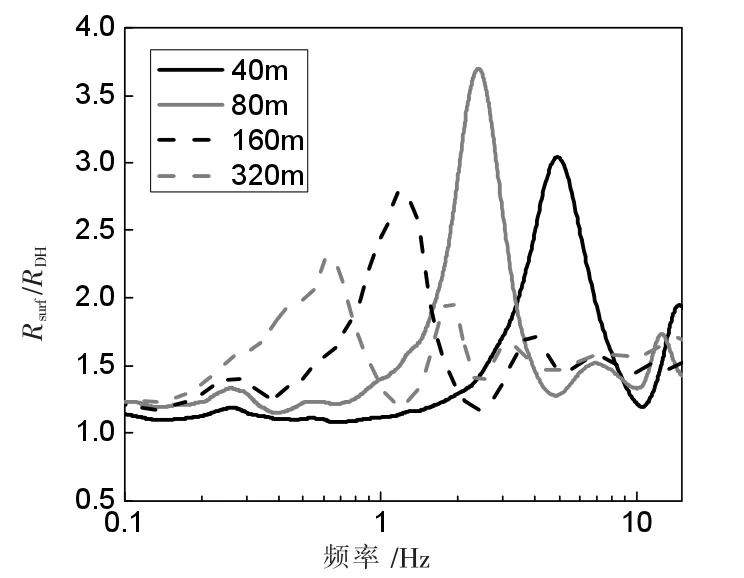
图2 井下40 m到320 m的参考场地的Rsurf/RDH

为了将井下基岩谱比法来代替传统的标准谱比法，文献[23]使用8对KiK-net台站的加速度反应谱比（见图3）定性地分析井下基岩谱比法BSR与标准谱比法SSR的关系。这8对KiK-net台站是由8个土层台站及每个台站附近的露头基岩台站组成，计算露头基岩台站的地表记录/井下基岩记录的加速度反应谱比Rsurf/RDH(Ⅰ)，以及土层台站地表记录/井下基岩记录的加速度反应谱比Rsurf/RDH(Ⅱ)，通过这两个比值得出井下基岩谱比BSR与标准谱比SSR的关系。其中基本频率f0,Ⅱ为露头基岩台站Rsurf/RDH(Ⅰ)与地表基岩台站Rsurf/RDH(Ⅱ)的最大值所对应的频率，而基本共振频率f0,Ⅰ由地表基岩台站Rsurf/RDH(Ⅱ)的最大值所对应的频率确定。

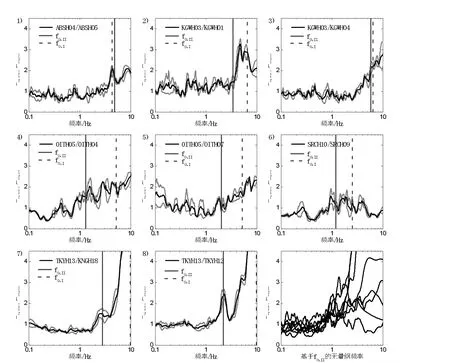
图3 8组场地的露头基岩（I）与井下基岩（II）的反应谱比以及8组场地的露头基岩和井下基岩的反应谱比

仅使用上述8组台站记录，很难从诸多地震影响因素（如局部的不均匀性、传播路径、二维效应等）中得出钻孔深度对场地的放大作用有何种数量关系。但从图3中可以看出，8组台站的Rsurf/RDH(Ⅰ)与Rsurf/RDH(Ⅱ)的比值与上述图2的结果相一致：低频的Rsurf/RDH比值接近1；频率从略低于f0,Ⅱ开始增加，且在高频时达到最大值。由于震源距较大，因此，对于不同场地高频段的Rsurf/RDH(Ⅰ)与Rsurf/RDH(Ⅱ)比值的差异，传播途径不太可能是其影响因素。而文中在筛选数据时考虑了基岩场地的场地影响（井下基岩场地存在异常的剪切波速），所以导致高频段的Rsurf/RDH(Ⅰ)与Rsurf/RDH(Ⅱ)比值差异的原因则可能为8个土层台站附近露头基岩场地的场地影响。

尽管少量场地及其记录相对于整个KiK-net台网不具有代表性，但图3得到的露头基岩台站Rsurf/RDH(Ⅰ)与地表基岩台站Rsurf/RDH(Ⅱ)比值至少定性地证实：井下基岩谱比BSR比标准谱比SSR有更高的幅值。

最后，利用筛选出的102组KiK-net台站的地表与井下记录得到地表与井下的傅里叶谱比BSR_F和理论数值模型来推导出场地的校正因子，该校正因子可以使井下基岩谱比BSR与标准谱比SSR相接近，从而直接利用单个台站的井下基岩谱比BSR推导出场地影响系数。其中，理论数值模型是利用102组KiK-net台站的地表记录（此时的地表记录为露头基岩地震动）和实际场地的土层资料得到，在计算传递函数时采用地表记录作为输入地震动，并选择弹性基底边界。这样，可以得出各层土的传递函数，其中地表传递函数TF是利用理论计算的土层地表地震动和输入地震动的比值，该传递函数对应于地表土层和露头基岩的比值。土层底部的传递函数TFDH是利用理论计算的土层底部地震动和输入地震动的比值，该传递函数对应于井下基岩和露头基岩的比值。钻孔传递函数BTF是利用TF/TFDH，该传递函数对应于地表土层和井下基岩的比值。而在这里，地表传递函数TF对应于KiK-net台站理论的标准谱比SSR，钻孔传递函数BTF对应于KiK-net台站理论的井下基岩谱比BSR_F。于是就可以考虑地表和井下的傅里叶谱比BSR_F与地表传递函数TF及钻孔传递函数BTF与地表传递函数TF之间的关系。

2.2 场地校正因子的拟合

为了得到地表和井下的傅里叶谱比BSR_F、地表传递函数TF及钻孔传递函数BTF之间的关系，利用所有KiK-net中BSR_F/TF的均值、所有KiK-net的数值模型的BTF/TF的均值及不同深度的反应谱比（Rsurf/RDH）model的均值（如图4（a）、（b）、（c）中的黑线）拟合出最佳的校正因子函数 DCF，该校正因子函数是通过拟合上述3个均值曲线得出的最优函数。

2.2.1 曲线拟合 采用文献[23]建议的拟合函数，即

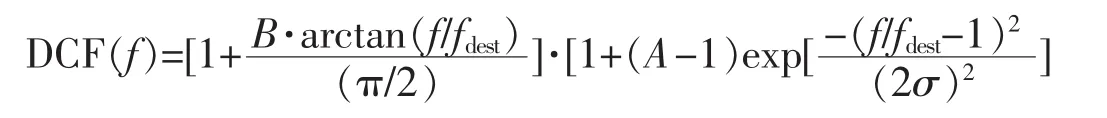
其中，fdest为台站的卓越频率f0，这里f/fdest定义为无量纲频率v，A、B、σ为拟合参数。

首先，对BSR_F/TF的均值、BTF/TF的均值和（Rsurf/RDH）model的均值这三组数据进行一次拟合，记为拟合1；然后，对三组数据进行多次拟合（图4（a）中为27次拟合，（b）为17次拟合，（c）为5次拟合），记为拟合2；对比三组数据给出自定义的B和σ值（这里B和σ值是根据拟合1和拟合2中的相应参数多次取值，并根据新参数重新拟合观察曲线得到的结果）；再根据给定后B和σ值进行一次拟合，记为拟合3；最后为了比较结果的好坏再利用三组数据进行二次拟合，记为拟合4，得到图4，并将确定系数Reduced Chi-Sqr和调整后的确定系数Adj.Reduced Chi-Sqr列于表1。

图4 拟合曲线

图4（a）虚线表示所有KiK-net中BSR_F/TF的均值，实线表示拟议的校正因子；图4（b）虚线表示基于所有KiK-net剪切波速资料的数值模型的BTF/TF，实线表示拟议的校正因子；图4（c）虚线表示不同深度的反应谱比（Rsurf/RDH）model均值，实线表示拟议的校正因子；曲线1为一次拟合曲线，曲线2为多次拟合曲线，曲线3为自定义拟合曲线，曲线4为二次拟合曲线；无量纲频率v=f/fdest。

表1 校正因子的模型参数和拟合优度参数

2.2.2 误差分析 上述SSE、MSE和RMSE越接近于0，说明模型选择和拟合更好，数据预测也越成功。Reduced Chi-Sqr称为方程的确定系数，Asjusted Reduced Chi-Sqr为调整后的确定系数，这两个值的取值范围为0～1，它们越接近1，表明拟合曲线的拟合效果越好。

将上述和方差SSE、均方差MSE、均方根RMSE列于表1，可以看出拟合2和拟合3的结果较拟合1和拟合4更小，而和方差SSE、均方差MSE、均方根RMSE其值越小则说明数据的离散性相对较小，虽然从表1中可以看出拟合2的拟合优度参数更优于较拟合3，但从图4（a）中看出拟合2在低频段误差相对较大。而一般曲线的不确定模型应考虑端点误差和曲线拟合误差的综合影响，由于在图4（a）中可以看出拟合2曲线的端点误差太大，故首先决定拟合2的结果不能作为拟合的最好选择，初步认为拟合3的拟合效果更好。

综合比较表1中的确定系数Reduced Chi-Sqr和调整后的确定系数Asjusted Reduced Chi-Sqr，排除拟合2可以看出拟合3的确定系数Reduced Chi-Sqr和调整后的确定系数Asjusted Reduced Chi-Sqr更大更接近于 1，所以最后的拟合曲线选择拟合 3，拟合参数如表1。 最终的拟合参数B=1.0，σ=0.16，比较图4（a）、（b）、（c）中的 A 参数，取最后的保守值 A=1.79，保留一位小数取 1.8。

2.3 对比分析

将Cadet[23]的校正因子拟合曲线与文中的校正因子拟合曲线作对比，如图5所示。首先通过比较文中与Cadet数据，如表2所示。

图5 文中、Cadet的拟合校正因子曲线

表2 文中、Cadet数据来源的比较

图5中显示，文中的拟合校正曲线位于Cadet拟合校正曲线之上，这是因为地震记录的震中距范围小于Cadet文章中震中距的范围，而近场放大远场抑制是地震动在土层传播中能量耗散的基本规律。

3 场地调整系数

场地调整系数计算时采用强震动记录的相对速度反应谱谱比来替换传统的傅氏谱谱比，主要原因是低阻尼比的相对速度反应谱在波形上近似于傅里叶幅值谱，而且传统的傅氏谱谱比需要大量的平滑工作，在平滑函数和平滑次数上还依赖于人为主观因素，造成谱比结果较大且有不确定性。这种谱比计算方式已广泛应用于场地效应评估研究中[24-25]。

参照《地震动参数区划图GB18306-2015》[1]中地震动峰值加速度分区值方法，将KiK-net台站按场地类别（Ⅰ、Ⅱ、Ⅲ、Ⅳ）和地震动输入水平（地震动输入水平分为 6 个区间：0.04g～0.09g、0.09g～0.14g、0.14g～0.19g、0.19g～0.28g、0.28g～0.38g、0.38g～0.75g）进行分类。 在完成分组后，利用每个台站的地表和井下的实际地震动记录，计算地表地震动和井下地震动的相对速度反应谱比，然后将该谱比除以校正因子曲线得到修正后的相对速度反应谱比，并按照上述分类的组别分别求几何平均值。最后按照周期范围0.1～0.5 s内的平均值得到场地的放大倍数，并假定Ⅱ场地的放大倍数为1，将Ⅰ、Ⅲ、Ⅳ类场地的放大倍数除以Ⅱ类场地的放大倍数，得到Ⅰ、Ⅲ、Ⅳ场地相对Ⅱ类场地设计的场地影响系数Fa与场地类别和峰值加速度的关系，由此再得到场地地震动峰值加速度调整系数Fa（短周期的放大系数）建议值，见表3。

表3 场地地震动峰值加速度调整系数Fa建议值

4 结论

（1）拟合的校正因子曲线的峰值对应于无量纲频率为1，并且拟合的校正因子曲线在低频的时候接近于1，高频的时候接近于1.8的平滑线。一般说来，台站在共振频率时场地的放大效应最明显，而在高频时场地受地震的作用逐渐趋于平缓，并稳定在一个定值。（2）综合表2和图5，文中的震中距的最大范围小于Cadet给出的震中距的最大范围，但得出的场地校正因子比Cadet的大，这样可以得出震中距对场地校正因子有一定的影响，并且震中距越大，则场地放大作用反而会逐渐变小。而地震对结构的影响主要是近震，文中对地震的震中距的选取是采用对结构影响最大的震中距范围。（3）得出场地地震动峰值加速度调整系数建议值如表3所示。

[1]中国地震局.中国地震动参数区划图：GB 18306-2015[S].北京：中国标准出版社，2015.

[2]中国建筑科学研究院.建筑抗震设计规范：GB 50011-2010[S].北京：中国建筑工业出版社，2016.

[3]BORCHERDT R D.Effects of local geology on ground motion near San Francisco Bay[J].Bull Seism Soc Am,1970,60：29-61.

[4]HARTZELL S H.Site response estimation from earthquake data[J].Bull Seism Soc Am,1992，82：2308-2327.

[5]FIELD E H,JACOB K H.A comparison and test o f various site-response estimation techniques,including three that are not reference site dependent[J].Bull Seism Soc Am,1995，85：1127-1143.

[6]KATO K,AKI K,TAKEMURA M.Site amplification from coda waves:validation and application to S-wave site response[J].Bull Seism Soc Am,1995，85：467-477.

[7]SU F,ANDERSON J G,BRUNE J N,et al.A comparison o f d irect S-wave and coda wave site amplification determined from aftershocks of Little Skull Mountain earthquake[J].Bull Seism Soc Am,1996,86：1006-1018.

[8]BONILLA L F,STEIDL J H,LINDLEY G T,et al.Site amplification in the San Fernando Valley,California:variability of site-effect estimation using the S-wave,coda,and H/V methods[J].Bull Seism Soc Am,1997,87：710-730.

[9]STEIDL J H,TU MARKIN A G,ARCHULETA R J.What is a reference site[J].Bull Seism Soc Am,1996,86：1733-1748.

[10]刘铮，沈健文，石树中，等.软土对基岩峰值加速度的放大作用[J].同济大学学报（自然科学版），2009，37（9）：607-611.

[11]赵艳，郭明珠，李化明，等.对比分析中国有关场地条件对设计反应谱最大值的影响[J].地震地质，2009，31（1）：186-196.

[12]栾极.设计反应谱场地放大系数和动力放大系数的研究[D].武汉：华中科技大学，2012.

[13]郭晓云，薄景山，巴文辉.汶川地震不同场地反应谱平台值统计分析[J].地震工程与工程振动，2012，32（4）：54-62.

[14]HWANG H H M,LIN HUI-JIE,HUO JUN-RONG.Site coefficients for design of buildings In eastern United States[J].Soil Dynamics and Earthquake Engineering,1997,16（1）：29-40.

[15]李小军，彭青.不同类别场地地震动参数的计算分析[J].地震工程与工程振动，2001，21（1）：29-36.

[16]吕悦军，彭艳菊，兰景岩，等.场地条件对地震动参数影响的关键问题[J].震灾防御技术，2008，3（2）：126-135.

[17]KINOSHITA S.Kyoshin Net（K-NET）[J].Bull Seismol Soc Am,1998,69（4）：309-332.

[18]MALAGNINI L,MAYAYEDA K.Estimating absolute site effects[J].Bull Seismol Soc Am,2004,94（4）：1343-1352.

[19]OTH A,BINDI D,PAROLAI S,et al.Spectral analysis of K-NET and KiK-net Data in Japan,Part II:On attenuation characteristics,sourcespectra,and site response of borehole and surface stations[J].Bull Seismol Soc Am,2011,101（2）：667-68.

[20]郭锋.抗震设计中有关场地的若干问题研究[D].武汉：华中科技大学，2010.

[21]崔昊，丁海平.基于KiK-net强震记录的场地调整系数估计[J].地震工程与工程振动，2016，36（4）：147-152.

[22]TAKAJI KOKUSHO,KATSUHARU SATO.Surface-to-base amplification evaluated from KiK-net vertical array strong motion records[J].Soil Dynamics and Earthquake Engineering,2008,28：707-716.

[23]CADET H,PIERRE-Y B,ADRIAN R-M.Site effect assessment using KiK-net data:Part 1.A simple correction procedure for surface/downhole spectral ratios[J].Bull Earthquake Eng,2012,10：421-448.

[24]ZHAO J X,IRIKURA K,ZHANG J.An empirical site classification method for strong motion stations in Japan using H/V response ratio.Bull Seismol Soc Am,2006,96（3）：914-925. [25]WEN R Z,REN Y F,ZHOU Z H,et al.Preliminary site classification of free field strong motion stations based on Wenchuan earthquake records[J].Earthquake Science,2010,23（1）：101-110.

Estimation and application of depth correction factor for site coefficient based on KiK-net strong-motion seismograph network

BIAN Fangdong,DING Haiping
（Jiangsu Key Laboratory of Structure Engineering,SUST,Suzhou 215011,China）

There are large amounts of acceleration records both at ground surface and at the bottom of boreholes of KiK-net strong-motion seismograph network,which provides the basis for the analysis of the site effect.In order to ensure the rationality of statistical results,the article selected the strong-motion records such as magnitude,epicentral distance and focal distance,and selected 1 233 sets of data records from 102 KiK-net stations.Using these records and site coefficient of correction factor method proposed by Cadet,this article calculated and fitted the site coefficient correction curve based on the soil depth.Then,according to the site coefficient of correction factor,the site influence coefficient Fa was calculated and the suggested value of the influence coefficient of different site was given.The results show that the depth correction factor estimation has a potential value for the site adjustment coefficient based on the current China code provision.

KiK-net strong-motion seismograph network;amplification factor;correction factor;site coefficient

秦中悦）

P315.9

A

2096-3270（2017）04-0014-06

2016－02-27

国家自然科学基金项目（51278323）；江苏省“333高层次人才培养工程”科研项目

卞方东（1991-），男，安徽天长人，硕士研究生。

丁海平（1969-），男，教授，博士，从事地震工程及防灾减灾工程研究，Email：ustsgjg@163.com。