函数Lipschitz连续的一个充要条件

彭康青，马振明

（1.陇南师范高等专科学校，甘肃成县 742500；2.西北师范大学，甘肃兰州 730070）

函数Lipschitz连续的一个充要条件

彭康青1，马振明2

（1.陇南师范高等专科学校，甘肃成县 742500；2.西北师范大学，甘肃兰州 730070）

导函数有界是函数f( x)在区间I上Lipschitz连续的充分条件，文章证明了它同时也是必要条件。

Lipschitz连续；有界；充要条件

在分析学科，特别在微分方程中，常要求函数Lipschitz连续[1]。于是，关于函数Lipschitz连续的判定就显得十分重要。对于区间I上的可导函数我们已经知道，其导函数有界是其在I上Lipschitz连续的一个充分条件[2]。本文证明这一条件也是必要条件。

证明 设M是集合B的上界，即对任何x和x0∈I，且 x≠x0，有

由函数 在点x0∈I可导，即得，即M也是集合A的上界。

推论 supA=supB。

证 由supB是集合B的上界，即得supB也是集合A的上界，于是就有supA≤supB。

的上界，因此，又有supA≥supB。于是得supA=supB。

综上，可以得出以下结论：

在区间[0，1]上的Lipschitz连续性。

解 该函数在区间[0，1]上可导。由定理3，考察其Lipschitz连续性可归结为考察其导函数在区间[0，1]上的有界性，于是有

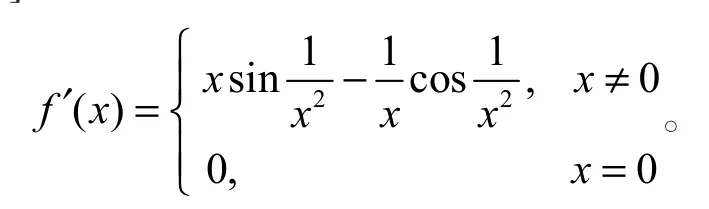
解 该函数在区间（0，+∞）内可导。由定理3，这里的问题是确定α的取值范围，使函数在区间（0，+∞）内有界。易见 α＞1或 α＜0时在（0，+∞）内无界。

当 0＜ α＜1 时，注意到 x→0+时 sinxα～xα，就有

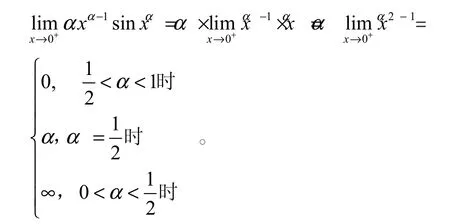
［1］东北师范大学微分方程教研室．常微分方程（第二版）［M］.北京：高等教育出版社，2005：78．

［2］马振民．数学分析的方法与技巧选讲［M］．兰州：兰州大学出版社，1999：51.

［3］王娇娇，李军.局部 Lipschitz连续函数差的刻画［J］.四川理工学院学报（自然科学版），2014，27（1）：94-97.

［4］刘亚军，范胜君.用Lipschitz函数序列一致逼近一致连续函数［J］.高等数学研究，2015，18（5）：7-9.

A Sufficient and Necessary Condition for the Continuity of Function Lipschitz

PENG Kang-qing1，MA Zhen-ming2
（1.Longnan Teachers College,Chengxian 742500，China；2.Northwest Normal University,Lanzhou 730070,China)

Derivative functionis bounded,which is the sufficient condition to assure the Lipschitz continuity of function in the interval I.In this paper we prove the condition is also necessary.

Lipschitz continuity；boundedness；sufficient and necessary condition

O17

A

1674-3229（2017）04-0009-02

2017-06-20

甘肃省陇南市科技计划项目（2016-21）

彭康青（1968-），女，陇南师范高等专科学校数信学院副教授，研究方向：数学分析。