基于流体网络的人体血液体循环分析

徐 克 赵良举 李明阳

（重庆大学动力工程学院低品位能源利用技术及系统教育部重点实验室，重庆 400030）

基于流体网络的人体血液体循环分析

徐 克 赵良举∗李明阳

（重庆大学动力工程学院低品位能源利用技术及系统教育部重点实验室，重庆 400030）

基于中医脉诊原理，研究人体各器官流阻变化对血流动力学参数的影响。建立人体血液体循环流体网络模型，采用10次谐波血流动力学表达式模拟心脏输出。改变各器官流阻，流阻比η分别取值0.5、1.0、1.5、2.0、2.5、3.0，利用平均法求解模型。假设心输出量一定，结果表明：随着流阻增大对应分支流量下降；不同分支流阻增大均能使主动脉平均压力上升，当流阻比η＝3.0时，脑、肝、肾、胃、肠、脾分支流阻增大引起主动脉压力较正常值分别增大23.29%、16.42%、14.67%、9.69%、9.59%、7.82%；肝和肾分支流阻变化对桡动脉影响较大，当流阻比η＝3.0时，桡动脉压力较正常值分别增大22.85%和11.17%，而其他器官分支流阻变化对桡动脉影响很小；对于桡动脉压力谐波振幅，脑分支流阻变化的影响最大，其次是肝和肾，而胃肠脾的影响很小。可见，该模拟研究方法可以得到人体血流动力学参数与各器官流阻变化之间的理论联系，为中医脉诊提供一些理论依据。

体循环；流体网络模型；血流动力学；平均法

引言

流体网络分析在很多领域中都有广泛应用。在生物动力学领域中，人体血液循环系统是一种周期性受迫的复杂流体网络，通过对其建模，可以得到血液流量、压力等血流动力学参数。

在人体血液循环系统建模中，主要采用电路网络模拟和流体网络解算两种方法，而早期研究采用电路网络模拟较多。国外，Mcleod等建立PHYSBE模型［1］，这是一个经典的线性循环系统模型。该模型主要包含左心、主动脉、上肢、下肢、头部、躯干、腔静脉、右心、肺循环部分这九大模块。Rideout等建立整个心血管系统的电路模型，包含主动脉和主静脉等分支结构，对体循环和肺循环系统进行了系统研究［2］。Alessandro等建立具有动脉压力感受器反射控制的心血管耦合数学模型，研究表明，血管阻力波动会造成压力缓冲从而导致血压变化，得到心脏周期与血压之间的正相关关系［3］。由Harvard-MIT建立的心血管系统仿真模型RCVSIM（research cardiovascular simulator）［4］，该模型主要由 3 个模块组成：一是系统的集总参数模型，主要由心脏部分和体循环部分构成；二是实时调节系统模型，包括动脉反馈系统、心肺循环反馈系统等；三是人体静息时物理扰动模型，包括呼吸作用、外界扰动动脉血管时血管阻抗的自动调节等。国内，对生理系统建模的研究较多的有白净、郑振声、樊瑜波、郑泰胜、郝卫亚等人［5-9］，他们建立含多分支的体循环模拟、冠脉循环的仿真、灌注压对左心室壁心肌层间血流影响、左心室心肌局部缺血的模型、心肺交互的心血管系统模型等。血液循环系统建模采用流体网络解算方法的较少，具有代表性的是Hillen等根据Willis解剖图建立的脑循环Willis环等效流体网络结构模型［10］。该模型通过采用平均法分析脑梗塞和椎动脉狭窄病变，得到与临床相符的结果，表明流体动力学方法在心血管系统建模的可行性。

人体血液脉搏波在主动脉近心端产生，经过血液循环系统将血流动力学信号传播到人体桡动脉，中医脉诊正是通过桡动脉的脉搏信号来诊断疾病。本研究基于中医脉诊原理，希望通过模拟计算得到各器官流阻变化对人体血流动力学参数的影响关系，为中医脉诊提供客观依据。当人体器官出现病变时，其血液流动阻力会发生变化，从而对血液循环流体网络造成影响。赵良举提出经络呼吸辅助系统假说［11］，认为当内脏器官出现炎症等症状时，代谢加强、CO2产生增多，如果不能及时排出，局部流阻和压力将增大，造成局部血液循环障碍。针刺穴位可以通过经络将CO2排出从而降低血流阻力，起到疏经活血的作用。

由于人体血液循环系统的复杂性，目前对包含人体主动脉、主要动脉分支、主要器官动脉及毛细血管网分支、四肢动脉及毛细血管网分支和主要静脉分支等的血液流体网络研究很少。本研究采用流体网络建模方法模拟人体血液体循环系统，分析人体各器官流阻变化对血流量、压力等血流动力学参数的影响关系。

1 方法

1.1 概述

首先，建立人体血液体循环流体网络模型，如图1所示。根据流体网络理论将模型分为树和连支两部分，计算模型中每条分支的参数。其次，采用10次谐波血流动力学表达式模拟左心室动脉血流输出信号。最后，通过改变各器官流阻，利用自适应控制方法中的平均法分别求解模型。

在求解过程中，假设心输出量一定，同时将人体器官病变等价为模型中各器官分支流阻的变化。本研究通过建模计算，得到不同器官流阻变化对相应分支的血液流量，主动脉和桡动脉平均压力以及桡动脉压力谐波振幅的影响关系。

1.2 模型的建立

1.2.1 模型简介

流体网络建模具有如下特点：首先，流体轴向流动速度远大于其横向流动速度，因而可以略去横向流动速度分量，且认为所有流动参数（流量、压力等）是在沿管路横截面上求平均值的；其次，流动参数是轴向距离与时间t的函数，称为一元不定常流动；再次，流体网络动力波形可以是正弦波、矩形波，也可以是按一定函数规律变化的规则与不规则波形；最后，流体传输与瞬变往往是在以网络形式出现的管网中进行的。

人体血液循环系统属于复杂流体网络，从而具备上述所有特点。此外，血液管内流动还受血流惯性、黏性、压缩性、血管几何形状和大小等因素影响。所以，建模过程中还需要作出以下假设：血液是牛顿流体，且不可压缩；血管的顺应性是线性的；不考虑血管瓣膜的防倒流机制；人体血液循环流体模型可以使用集总参数模型求解。

本研究在前人建立的心血管系统电路模型、RCVSIM的集总参数模型、体循环动脉模型和脑循环Willis环流体网络模型等的建模思路下，结合人体主要血管分布，创新性地建立人体血液体循环流体网络模型，如图1所示。

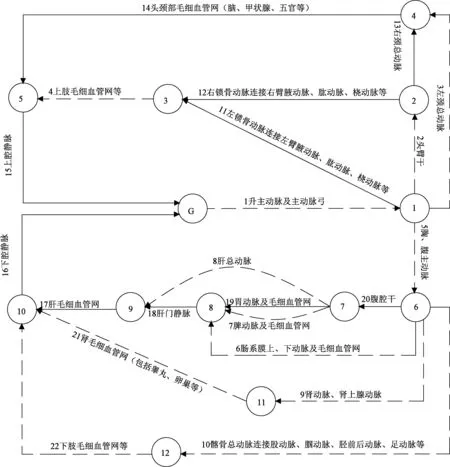
图1 人体血液体循环流体网络模型Fig.1 The fluid network model of systemic circulation of human blood

在体循环建模过程中，将心脏模拟成一个泵，作为模型的动力执行机构，在图1中由G点表示。模型中其他小圈中的数字分别代表流体网络模型的各个计算节点，节点与节点之间的连线（实线和虚线）表示简化的各类血管段分支。每条血管分支把同类血管视为并联，不同类血管视为串联。每条分支代表的血管类型在模型中已详细地标示。模型中主要反映人体主动脉及其动脉分支和器官动脉及其毛细血管网分支等，同时将静脉简化为上下腔静脉回流分支。

网络模型结构中共有22条分支，其中独立分支数n＝20（1～20），独立节点数nc＝11（在计算过程中，将节点1的压力等价为主动脉压，节点3的压力等价为桡动脉压）。根据流体网络理论［12］，网络连支数l＝n-nc+1＝10，网络树支数为n-l＝10。选择该流体网络11～20分支作为网络的树支（实线），对应的分支参数的角标为a。选择2～10分支作为网络的连支（虚线），对应的分支参数的角标为c。连支1为模型的动力连支。网络树枝模型不包含动力执行机构。

1.2.2 模型参数

流体网络建模过程中已经假设血液是牛顿流体且不可压缩，则血液在每根血管内的流动可以认为是泊肃叶（Posiseuille）流［13］，则根据泊肃叶定律，有

式中：Q为通过某一段血管血液流量，mL/s；ΔP为每条血管分支的压降，mmHg；μ为血液黏度，Pa·s；r为血管半径，cm；l为血管长度，cm。

根据流阻定义计算公式，有

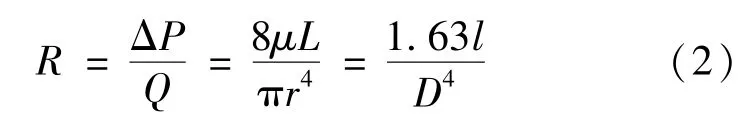
式中：R为血管流阻，dyn·s/cm5；D为血管直径，cm。

由式（2）可知，如果给出血液循环流体网络模型中每条分支的压降以及各条分支的血流分布，则可以得到相应分支的流阻大小。由式（2）还可知，血管流阻的大小可视为血管长度l与直径D的函数，即求出每条分支的流阻和已知的每条血管分支的长度，则可以得到每条血管分支的等效直径和横截面积。表1、2分别表示通过文献总结的人体血管构型及其内压和人体平静时各器官的血流量分布情况［14-15］。

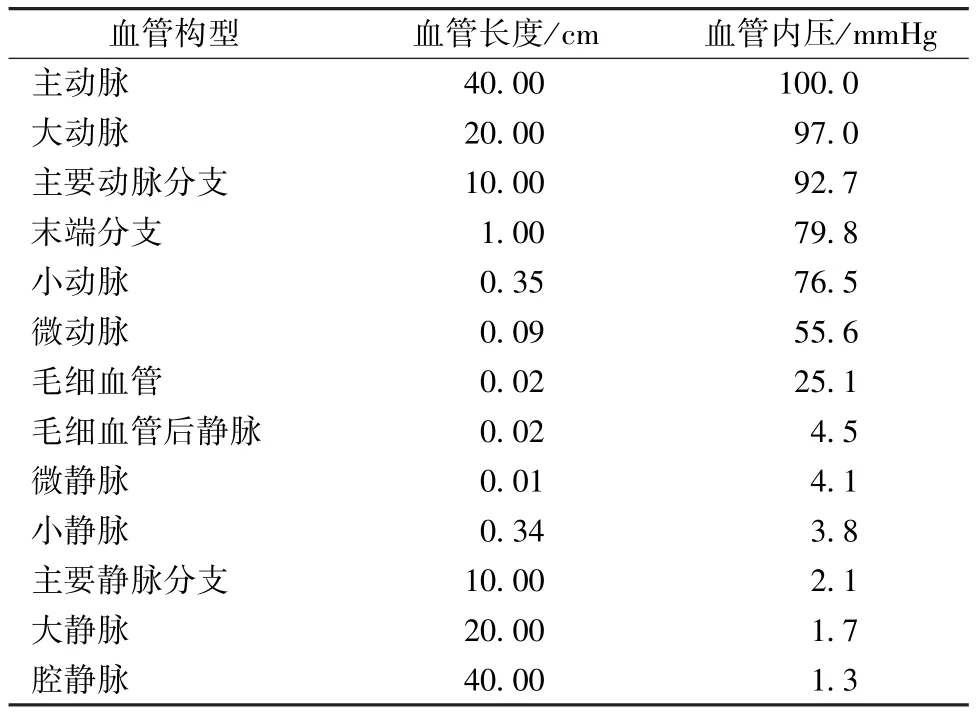
表1 血管构型及其内压Tab.1 The intravascular pressure of different configurational blood vessels

表2 人体平静时各器官血流量Tab.2 The blood flow of each organ in a calm state

定义血液流体阻力系数T值的计算公式为

式中：ρ为血液密度，取值1.056 g/cm3；S为血管横截面积，cm2。

由表1、2设定的对应分支流量初始值及分支压降，则可通过式（2）、（3）计算得到网络各分支流阻R及阻力系数T等参数，如表3所示。

表3 模型参数计算结果Tab.3 Calculated results of model parameters

1.3 血流动力学表达式

将每次心脏输出的时间间隔作为一个周期Tn，心脏输出的血液流量或压力波f（t）可分解为各种简谐波的组合［16］。当心跳速率为72次/min时，心跳的第一谐振波频率即为1.2 Hz，第二谐振波频率为2.4 Hz，第三谐振波频率为3.6 Hz……心跳的第一谐波振幅C1，第二谐波振幅C2，第三谐波振幅C3……可以视为血液分配在各种频率的能量指标。由于心脏输出信号的直流部分Q0与C1、C2、C3等10次谐波的能量已占了脉搏能量的大部分，所以采用10次谐波就可以模拟心脏输出的血流动力学的血流表达式，即

其中，脉搏谐波频谱分析［16］如表4所示。

1.4 平均法

血液循环流体网络模型中每一条分支均可以用如下流体动力学方程来描述［17］，即

表4 人体脉搏谐波频谱分析Tab.4 Harmonic spectrum analysis of human body pulse

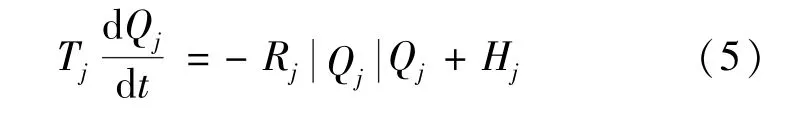
式中，Qj是通过分支j的流体流量，Rj是流体阻力，Hj是分支压降，Tj是阻力系数。

根据式（3）的定义，阻力系数可表示为

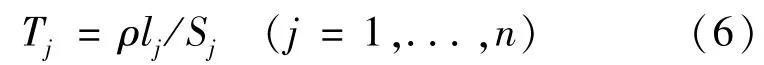
式（5）的向量形式为

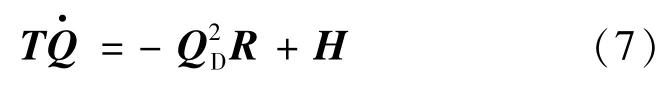
如同一个电网络，流体网络也满足Kirchhoff电流定律，即任何节点流体流出量等于流入量。因此，流体网络的Kirchhoff电流定律可以表示为

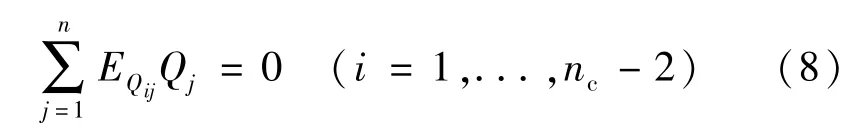
或

式中，EQ＝［EQc｜EQa］，nc表示网络节点数，Q是流量矩阵，EQ＝［EQij］是一个（nc-2）×n的满秩矩阵。

EQij的值定义如下：如果分支j与节点i相连且流体流出此节点，则EQij＝1；如果分支j与节点i相连且流体流入此节点，则EQij＝-1；如果分支j与节点i不相连，则EQij＝0。

通过对周期性受迫血液循环流体网络进行网络建模，并利用平均法进行分析，可得到如下结论［18］，定义矩阵为

式中，矩阵Tc和Ta分别代表流体网络连支和树支的阻力系数的对角矩阵，EQc是将EQ＝［EQc｜EQa］中将EQa化为单位矩阵得到的连支网络系数矩阵。定义矩阵为

式中，Qc0（R，E，Q0）表示l维二次方程组的解，即

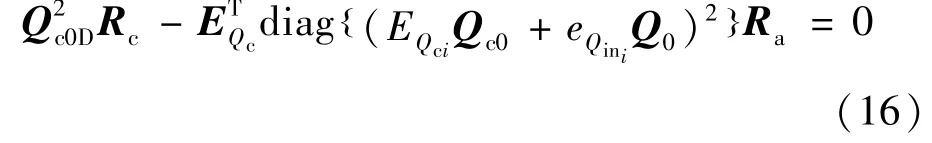
此非线性方程组只有数值解而无解析解，采用Matlab中fsolve函数进行迭代求解，将解代入矩阵V和W，得到的矩阵V为非奇异，且是Hurwitz的，且对于给定的Q0＞0，存在足够小的Ck和足够大的ω，使描述的流体网络系统渐近指数收敛到的领域，将以上计算结果代入下列方程组，即可得到流体网络各连支和树支的平均流量矩阵表达式，有

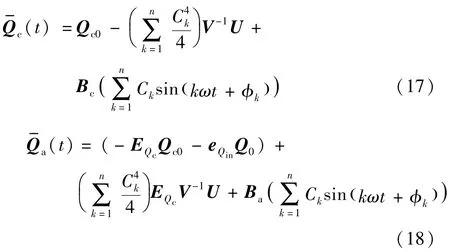
平均系统不依赖于相应的相位φk［19］。按照上述计算方法，得到流体网络模型中各分支流量方程，通过计算也可以求出各节点压力表达式。

2 结果

定义无量纲流阻比η＝R′/R，其中R′和R分别表示变化后的流阻和正常流阻，则η反映器官分支流阻的变化情况。器官病变将导致流阻增大，一般η＞1，分别取值1.5、2.0、2.5和3.0进行模拟计算。为对比分析，同时计算η取0.5和1.0的情况。

2.1 流阻变化对血流量的影响

研究表明，在心输出量一定的条件下，不同器官分支血流量都会随其流阻的增大而减小。下面给出了肝分支血流量随流阻变化情况，如图2所示。由图可知，随着η的增大，流量幅值下降。计算得出，肾、胃、肠、脾和脑分支的血流量随相应分支流阻变化的趋势与肝分支一致。

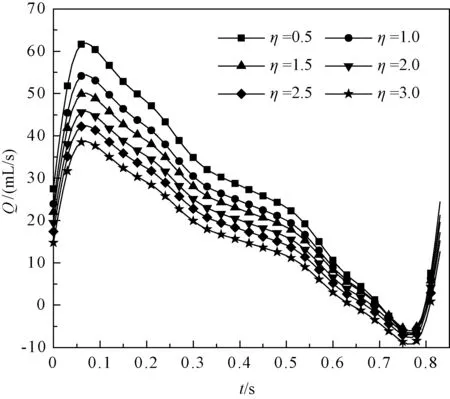
图2 肝分支血流量随其流阻变化Fig.2 Change of liver branch flow rate with the flow resistance

2.2 流阻变化对主动脉和桡动脉压力的影响

图3、4分别表示肝分支流阻对主动脉和桡动脉压力的影响关系。研究表明，在心输出量一定的条件下，主动脉和桡动脉压力幅值随肝分支流阻的增大而均增大，且由图可知，肝分支流阻变化对主动脉和桡动脉压力影响都非常明显。计算得出，随着肾分支流阻增大，主动脉和桡动脉压力也均增大，但肾分支流阻变化对主动脉和桡动脉压力的影响比肝分支较小。

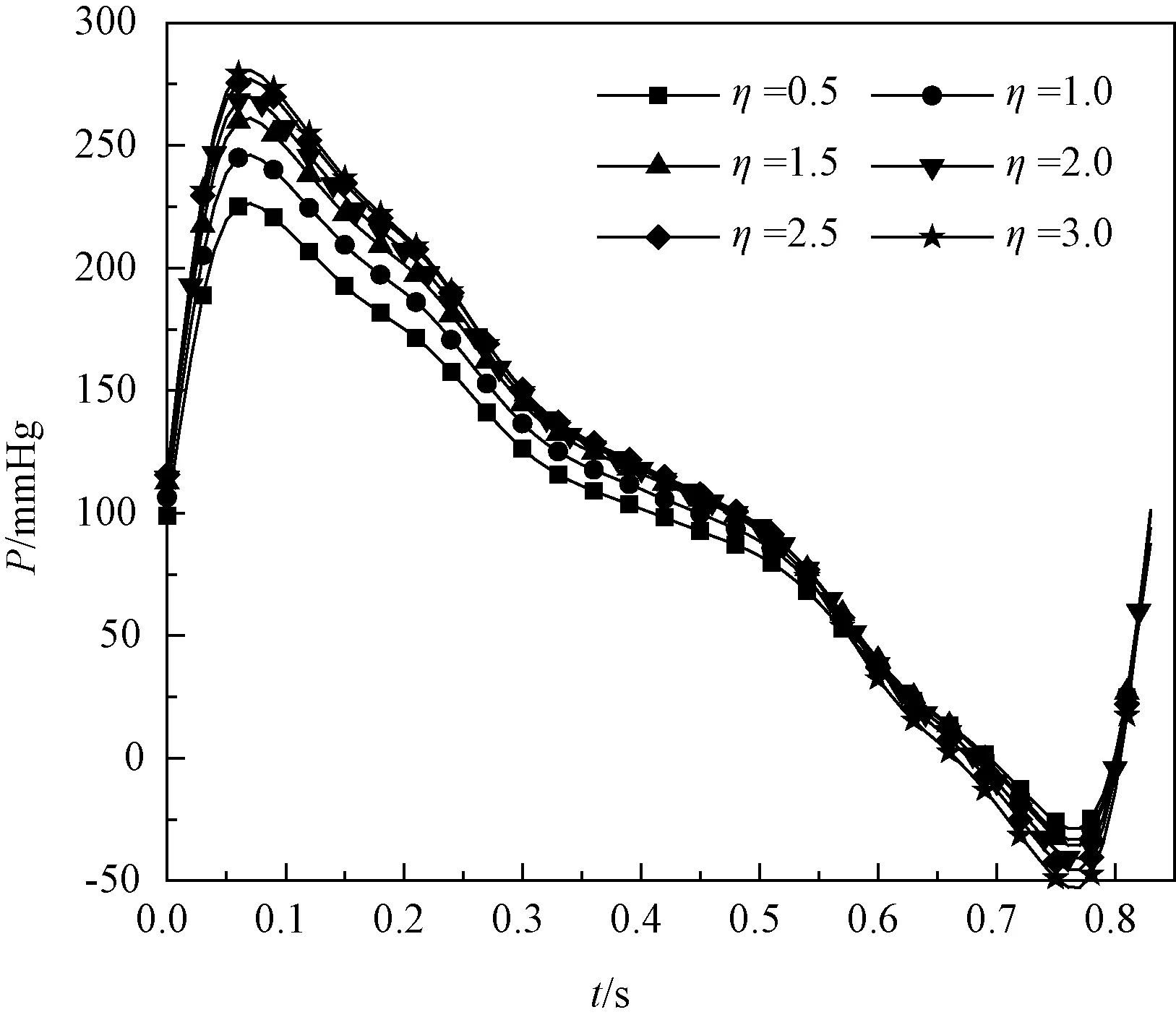
图3 主动脉压力随肝分支流阻变化Fig.3 Change of the aortic pressure with the liver branch flow resistance

图5、6分别表示胃分支流阻变化对主动脉和桡动脉压力的影响关系。从图5可以看出，当胃分支流阻增大时主动脉压力幅值增大，但增大的趋势较小；从图6可以看出，胃分支流阻变化对桡动脉压力的影响很小。通过与胃分支对比，脾和肠分支流阻变化对主动脉和桡动脉压力的影响和胃分支基本一致。

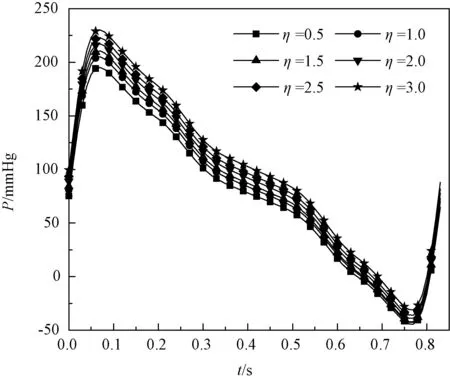
图4 桡动脉压力随肝分支流阻变化Fig.4 Change of the radial artery pressure with the liver branch flow resistance

图5 主动脉压力随胃分支流阻变化Fig.5 Change of the aortic pressure with the stomach branch flow resistance

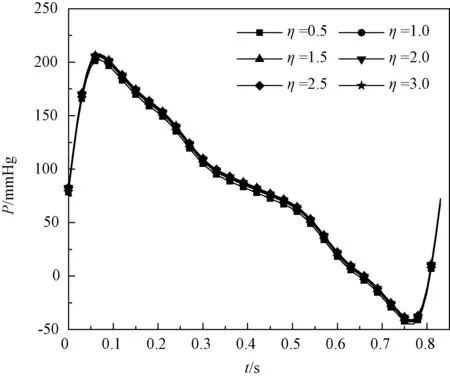
图6 桡动脉压力随胃分支流阻变化Fig.6 Change of the radial artery pressure with the stomach branch flow resistance

图7、8分别表示脑分支流阻变化对主动脉和桡动脉压力的影响关系。从图7可以看出，随着脑分支流阻增大，主动脉压力增大，且相比于其他器官分支，脑分支流阻变化对主动脉压力的影响最大。但从图8可以看出，脑分支流阻变化对桡动脉压力影响较小。

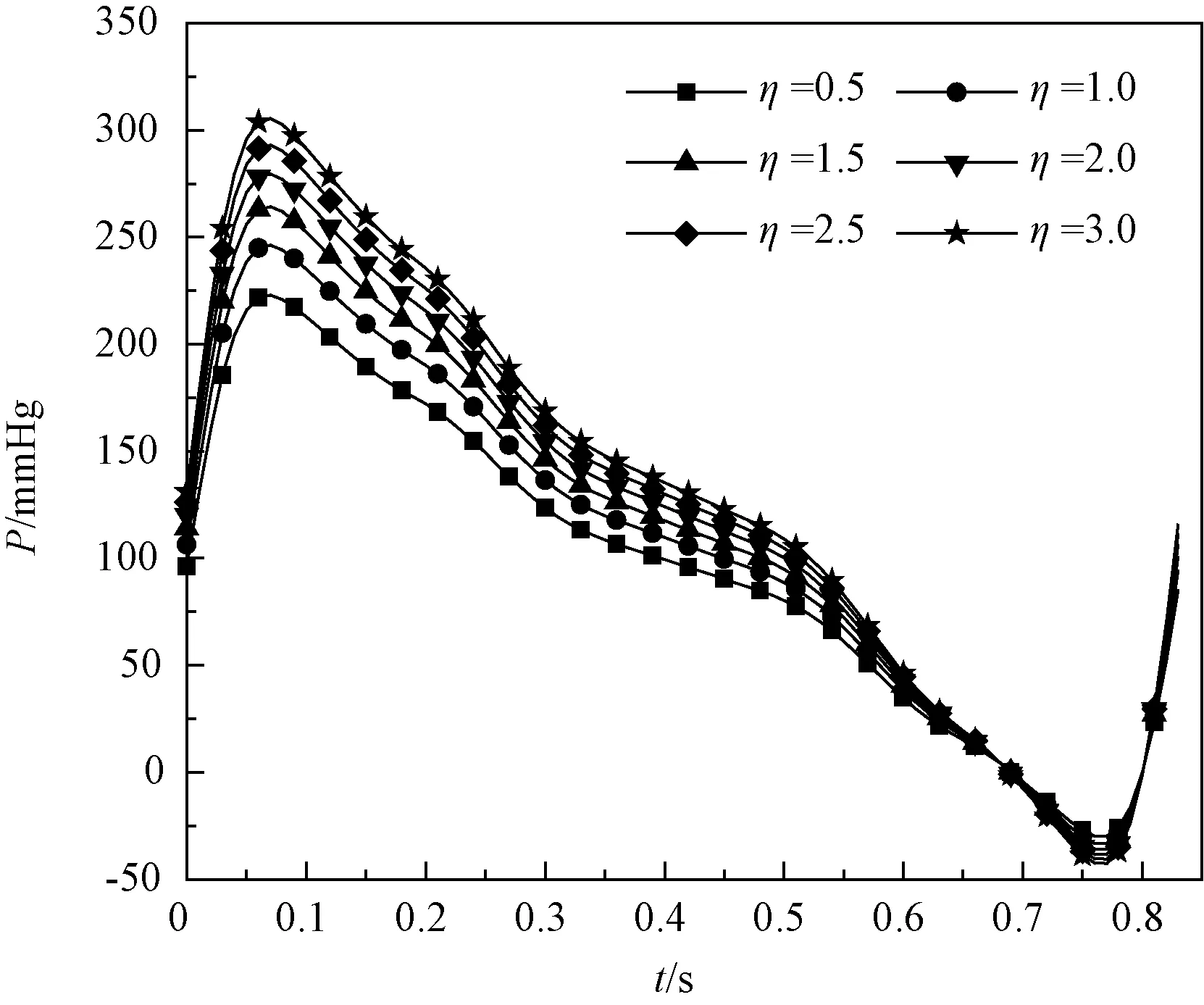
图7 主动脉压力随脑分支流阻变化Fig.7 Change of the aortic pressure with the brain branch flow resistance

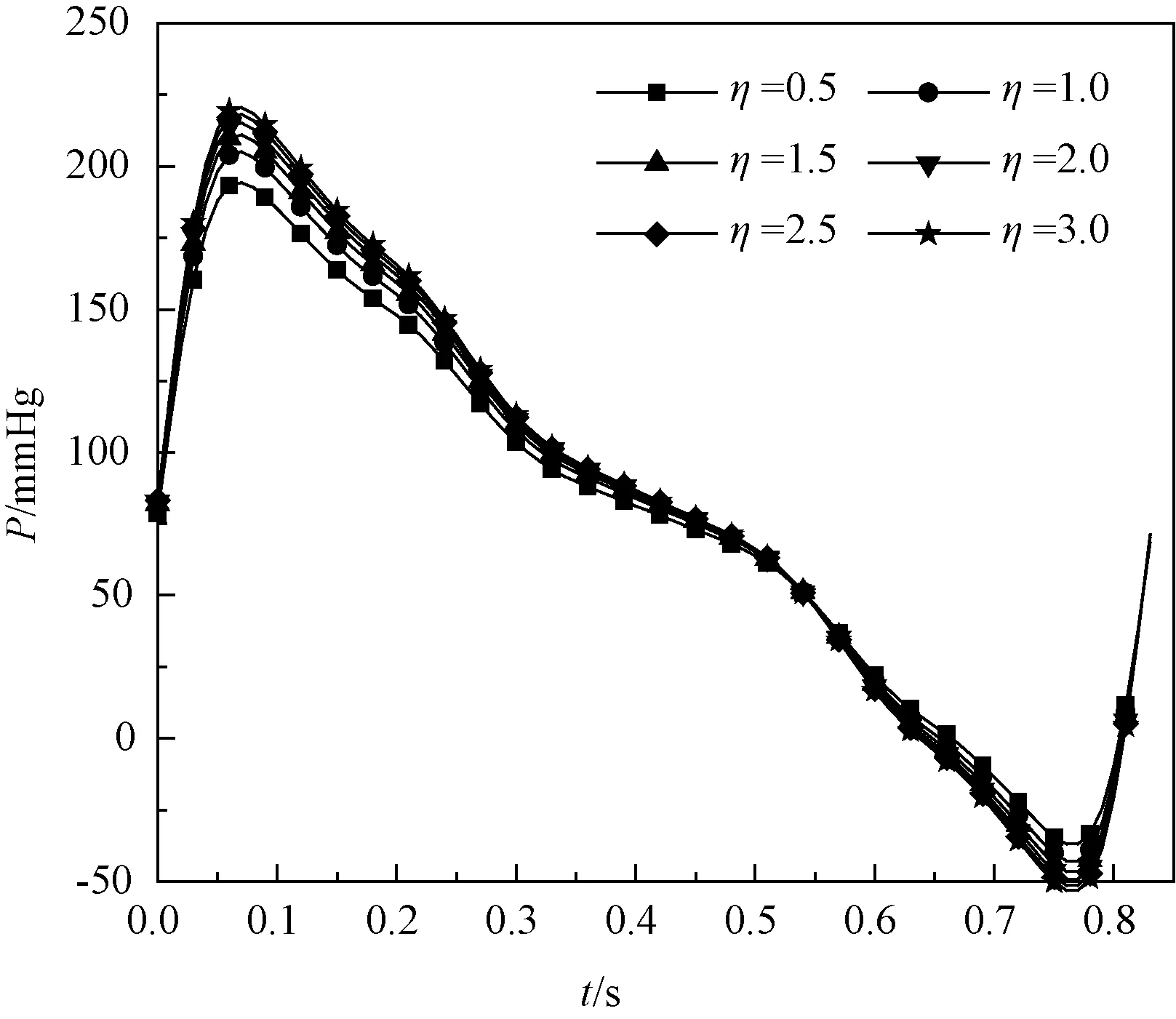
图8 桡动脉压力随脑分支流阻变化Fig.8 Change of the radial artery pressure with the brain branch flow resistance

对上述计算得到的主动脉和桡动脉压力谐波在一个周期内求傅里叶平均值，对比分析不同器官流阻变化对主动脉和桡动脉平均压力的影响关系。

不同器官流阻变化对主动脉平均压力影响的对比曲线如图9所示。由图可知，人体主动脉正常平均压力约为106.3 mmHg（η＝1.0时）。在心输出量一定的条件下，随不同器官流阻增大，主动脉平均压力均增大。当流阻比η＝3.0时，脑、肝、肾、胃、肠和脾分支流阻增大为3倍时，引起主动脉压力较正常值分别增大为23.29%、16.42%、14.67%、9.69%、9.59%和7.82%。

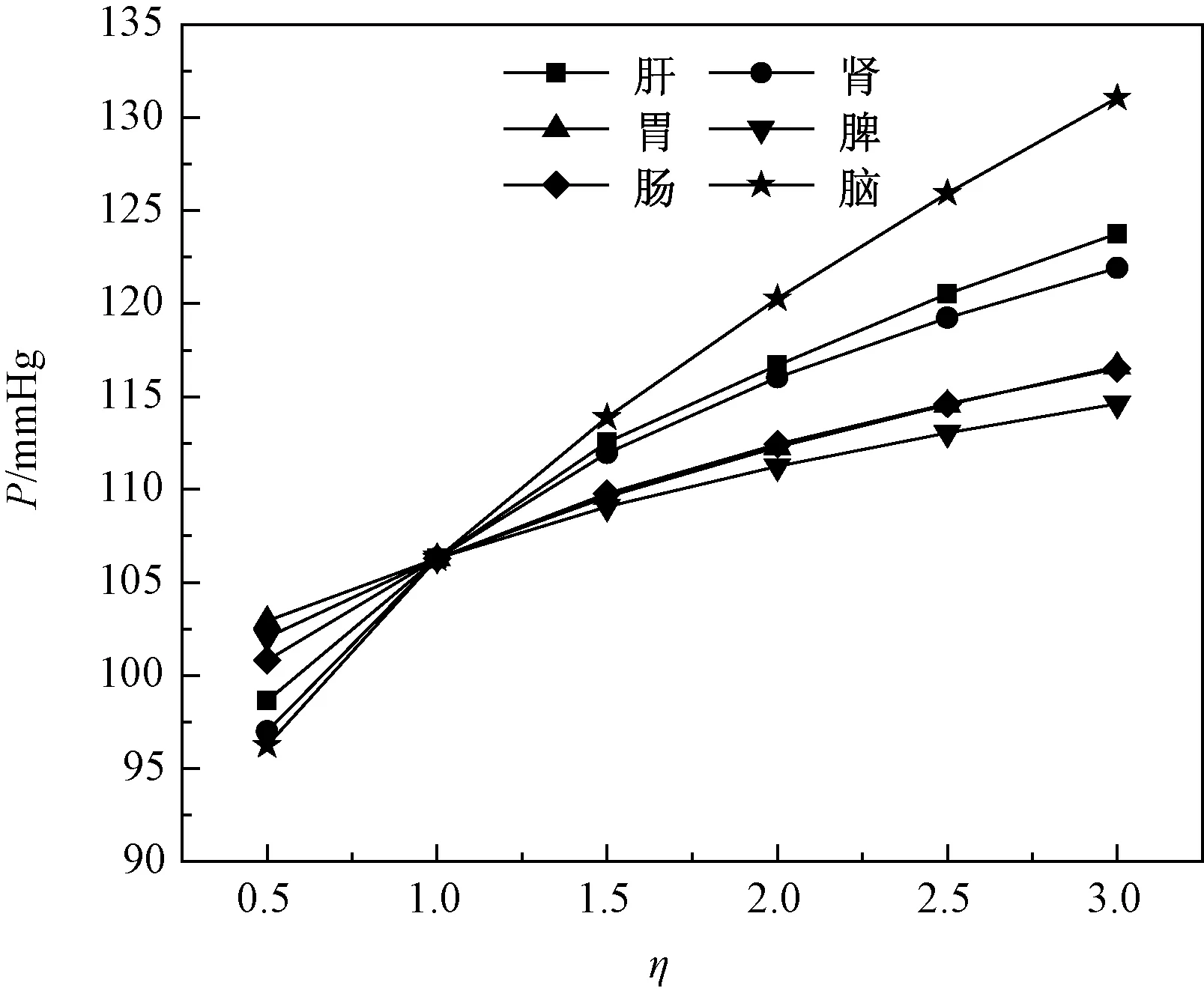
图9 主动脉平均压力随流阻变化影响对比Fig.9 Change of the aortic mean pressure with the flow resistance

不同器官流阻变化对桡动脉平均压力影响的对比曲线如图10所示。由图可知，人体桡动脉正常平均压力约为80.9 mmHg（η＝1.0时）。在心输出量一定的条件下，随不同器官流阻增大，桡动脉平均压力均增大。肝分支流阻增大对桡动脉的影响最为显著，且增大的趋势越来越大，肾分支流阻对桡动脉影响也较显著，胃肠脾和脑分支的影响较小。肝、肾、胃、肠、脾和脑分支流阻增加为3倍时，桡动脉压力较正常值分别增大22.85%、11.17%、2.92%，3.08%，0.98%和3.09%。

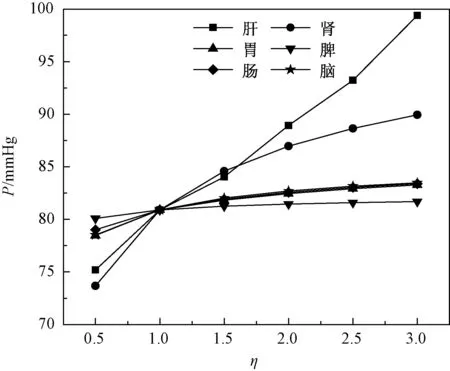
图10 桡动脉平均压力随流阻变化影响对比Fig.10 Change of the radial artery mean pressure with the flow resistance

2.3 流阻变化对桡动脉压力谐波的影响

对桡动脉压力谐波进行傅里叶变换，求出桡动脉各压力谐波振幅，并对比分析各器官流阻变化对不同谐波振幅的影响关系。

图11给出了桡动脉压力谐波振幅C1随各器官流阻的变化情况。计算得出，不同器官流阻变化对桡动脉压力其他谐波振幅的影响与C1一致。研究表明，脑分支流阻变化对桡动脉压力谐波振幅的影响最为显著，且呈平缓趋势，其次是肝和肾，而胃肠脾对桡动脉压力谐波振幅的影响很小且基本相同。

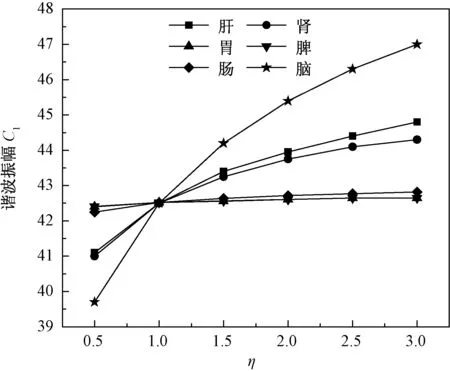
图11 桡动脉压力谐波振幅随流阻变化影响Fig.11 Change of the harmonic amplitude of the radial artery pressure with the flow resistance

3 讨论和结论

本研究表明，不同器官分支的流量随着该分支的流阻增大而减小，这为病理学“血瘀”［20］研究提供了依据。当人体器官出现病变时，其血流阻力增加，血流量下降，引起血液循环障碍最终导致病症的产生。中医经络理论认为，可以通过针灸、中药调理等治疗方法减小器官血流阻力，从而增加血液流量，促进其新陈代谢，恢复健康。

不同器官流阻变化对主动脉和桡动脉压力均有影响，这为中医脉诊提供了依据。研究表明，主动脉平均压力随不同器官流阻增大而增大，其中脑分支流阻增大对主动脉影响最大，其次是肝和肾，而其他分支影响较小。对于桡动脉平均压力，肝分支流阻变化对桡动脉的影响最为显著，其次是肾分支，而其他分支的影响较小。中医脉诊是根据人体桡动脉脉搏波信号来诊断疾病的，通过本研究得到了不同器官流阻变化与主动脉和桡动脉压力的理论联系。

王唯工提出心跳谐振波与器官共振的物理模型，以模拟体内血液循环与寸口脉诊波形的变化关系，并据此讨论各脏腑不同共振特性对血压波形的可能影响［16］。本研究也尝试讨论流阻变化对谐波振幅的影响关系，发现脑分支流阻变化对桡动脉压力谐波振幅的影响最为显著，其次是肝和肾，而胃肠脾对桡动脉压力谐波振幅的影响很小且基本相同。有关心脏输出信号谐波与各器官流阻之间的理论联系需要进一步深入研究探讨。

本模拟研究为体循环研究提供了一个新的方法，通过建模计算得到较好的理论结果，表明所建立模型的有效性及求解方法的可行性。目前与本研究内容相关的临床实践研究相当缺乏，具有代表性的是日本Takayama等的实验研究，涉及血液循环流阻变化，以及血流动力学参数与流阻的关系［21］。该实验通过针刺太冲穴位测量肱动脉和桡动脉的血管直径和血流量变化，发现针刺时肱动脉和桡动脉的血流量下降，针刺后180 s，肱动脉和桡动脉的血流量上升，他们认为针刺前后影响了植物神经的调节，使肱动脉和桡动脉的流动阻力发生改变，从而得到这样的实验结果。而赵良举的经络呼吸辅助系统假说，认为针刺太冲穴时，肝经内的气体释放，降低了肝的内环境压力，增加了肝毛细血管的渗透压，减少了肝毛细血管的阻力，使肝的血流量增加，相应的肱动脉和桡动脉血流量下降；针刺后肝毛细血管的阻力增加，肱动脉和桡动脉的血流量回升［11］。Shirai等针对文献［21］，建立了血流动力学模型并进行计算，得到与实验相符的结果［22］。本课题以器官病变等价为模型中相应分支流阻变化这一思想进行模拟研究，研究结果与文献［21-22］的研究结果相符合，从而使该理论研究有了一定的实验支撑，但仍需要进一步的临床实践验证。

［1］ Mcleod J.PHYSBE.A physiological simulation benchmark experiment ［J］.Simulation Transactions of the Society for Modeling＆ Simulation International，1966，7（6）：324-329.

［2］ Rideout VC. Mathematical and computer modeling of physiological systems ［M］.New Jersey：Prentice-Hall Inc，1991：1-65.

［3］ Alessandro S，Mauro U.Mathematical modeling of cardiovascular coupling：Central autonomic commands and baroreflex control［J］.Autonomic Neuroscience，2011，162（1-2）：66-71.

［4］ Goldberger AL，Amaral L，Glass L，et al. PhysioBank，PhysioToolkit，and PhysioNet：components of a new research resource for complex physiologic signals ［J］.Circulation，2000，101（23）：215-220.

［5］ 郑泰胜.冠状与系统循环血动力学关系的模型研究［J］.中国生物医学工程学报，1997，16（2）：108-114.

［6］ 樊瑜波，陈君楷.含动脉分支的体循环模拟实验系统 ［J］.实验力学，1995，10（1）：1-10.

［7］ 王怀阳，郑振声，吴晓明，等.灌注压对左心室壁心肌层间血流影响的建模与仿真研究 ［J］.医用生物力学，2000，15（3）：152-156.

［8］ 郝卫亚，李为慧，白净.左心室心肌局部缺血的生物力学模型及计算机仿真研究［J］.航天医学与医学工程，2001，14（5）：350-354.

［9］ 李新胜，白净，崔树起，等.心肺交互作用的心血管系统模型及仿真研究 ［J］.中国生物医学工程学报，2003，22（3）：241-249.

［10］ Hillen B，George F.Analysis of flow and vascular resistance in a model of the circle of Willis ［J］.Journal of Biomechanics，1988，21（10）：807-814.

［11］ Zhao Liangju.Acupuncture meridian of traditional Chinese medical science：An auxiliary respiratory system ［J］.Journal of Acupuncture＆ Meridian Studies，2015，8（4）：209-212.

［12］ 刘剑，贾进章，郑丹.流体网络理论 ［M］.北京：煤炭工业出版社，2002：1-185.

［13］ 丁光宏，覃开荣，高健，等.脑循环血液动力学研究：Willis环定常流力学模型［J］.中国生物医学工程学报，1998，17（1）：88-95.

［14］ 陆健敏，陈惠中，叶抗生.袖珍常用医学数据手册 ［M］.北京：金盾出版社，1996：15-25.

［15］ 唐元升，张秀珍，等.人体医学参数与概念 ［M］.济南：济南出版社，1995：63-78.

［16］ 张修诚，王唯工，陈荣洲，韩殿存.脉搏谐波频谱分析——中医脉诊研究新方法 ［J］.中国中西医结合杂志，1995（12）：743-745.

［17］ Hu Y，Koroleva OI，Krsti c′M.Nonlinear control of mine ventilation networks［J］.Systems ＆ Control Letters，2003，49（4）：239-254.

［18］ 隋金雪，杨莉.复杂流体网络分析与控制 ［M］.北京：电子工业出版社，2013：69-109.

［19］ 韩曾晋.自适应控制 ［M］.北京：清华大学出版社，1995：171-192.

［20］ 李同宪，李月彩.中西医融合观续——气血津液与内环境的融合［M］.西安：第四军医大学出版社，2012：71-78.

［21］ Takayama S，Seki T，Watanabe M，et al.Brief effect of acupuncture on the peripheral arterial system of the upper limb and systemic hemodynamicsin humans ［J］. Journalof Alternative ＆ Complementary Medicine，2010，16（16）：707-713.

［22］ Shirai A，SuzukiT，SekiT. Numericalreproduction of hemodynamics change by acupuncture on Taichong（LR-3）based on the lumped-parameter approximation model of the systemic arteries［J］.Integrative Medicine Research，2015，11（3）：161-170.

The Analysis of the Systemic Circulation of Human Blood Based on Fluid Network

Xu Ke Zhao Liangju∗Li Mingyang
（Key Laboratory of Low-grade Energy Utilization Technologies and Systems of Ministry of Education，College of Power Engineering，Chongqing University，Chongqing400030，China）

Hemodynamic parameters will be studied under the changes of different organs flow resistances，based on the principles of traditional Chinese medicine pulse diagnosis.A fluid network model of systemic circulation of human blood is established.Utilizing a 10 times harmonic hemodynamics expression of cardiac output and the average method of adaptive control，the model is solved whenηis respectively set to 0.5，1.0，1.5，2.0，2.5 and 3.0.With the cardiac index keeping constant，the results show that the average flow rate decreases with the increase of flow resistance of corresponding branch.The aortic mean pressure increases with the rise of flow resistance of organ branch.Whenηis setted to 3.0，the aortic mean pressure increases 23.29%，16.42%，14.67%，9.69%，9.59%and 7.82%higher than normal by the flow resistance increase of brain，liver，kidney，stomach，intestine and spleen branch respectively.The flow resistance of liver and kidney branch has the great effect on the radial artery mean pressure，which respectively increases 22.85%and 11.17%whenηis setted to 3.0.While the other organ branches have less influence.For the harmonic amplitude of the radial artery pressure，the biggest affecting factor is the brain branch flow.The liver and kidney branch have less influence than the brain.The stomach，intestine and spleen branch have little impact on it.In this paper，we have found the relationships between the hemodynamic parameters and the changes of different organs flow resistances by the simulation method，and it can provide some theoretical basis for traditional Chinese medicine pulse diagnosis.

systemic circulation；fluid network model；hemodynamics；average method

R318 文献标志码：A 文章编号：0258-8021（2017）05-0580-09

10.3969 /j.issn.0258-8021.2017.05.010

2016-08-17，录用日期：2017-04-07

∗通信作者（Corresponding author），E-mail：zhaolj@cqu.edu.cn