基于回归预测的肺4D-CT多相位配准

刘月亮 房诗婷 张 煜∗

1（南方医科大学生物医学工程学院，广州 510515）

2（广东省医学图像处理重点实验室，广州 510515）

基于回归预测的肺4D-CT多相位配准

刘月亮1，2房诗婷1，2张 煜1，2∗

1（南方医科大学生物医学工程学院，广州 510515）

2（广东省医学图像处理重点实验室，广州 510515）

针对由于灰度不均和局部形变较大引起的肺4D-CT图像配准精度不足问题，提出基于回归的逐块预测初始形变的方法。新方法的核心思想是：配准一幅浮动图像至参考图像时，利用与浮动图像相对应的不同相位的图像信息进行形变场预测。首先，利用已有配准算法配准不同相位的图像至参考图像，得到各图像对应的形变场；再将图像和对应形变场分块作为训练集，利用多维支持向量回归机建立回归模型；将浮动图像分块输入回归模型中，预测出初始形变场，从而得到中间图像，并最终细化配准中间图像与参考图像。采用由德克萨斯安德森肿瘤中心DIR实验室采集并公开的数据集，评价所提出的算法。实验量化评价结果表明，与传统的Active Demons算法、Spectral Log-Demons算法相比，图像的均方误差平方和显著降低（Active Demons算法49.34±23.92，Spectral Log-Demons算法31.81±15.09，所提出算法18.97±5.75，P＜0.05），相关系数显著提高（Active Demons算法0.952±0.022，Spectral Log-Demons算法0.967±0.015，所提出算法0.980±0.006，P＜0.05）。同时，视觉评价结果显示，所提出算法能够获得更准确的配准图像。

肺4D-CT；图像配准；形变预测；多维支持向量回归机

引言

在肺癌的诊断和治疗之中，肺4D-CT图像有重要的指导价值，它包含肺部呼吸运动信息，为肿瘤和放射区域的定位以及放射剂量的确定提供了真实依据。

肺4D-CT的配准是肺部医学图像分析的基础，其用途广泛，主要有肺部分割、利用配准传递像素标签［1］；跟踪肺部器官组织的运动，最大可能防止肿瘤的误诊和漏诊；同时，配准同一病人不同时间拍摄的肺部图像，可以监控疾病的发展与治疗效果等。

图像配准可映射为目标函数最优化的问题。针对肺部图像的配准，其精度受到以下因素影响：一是当前基于灰度配准方法的前提是假设图像对应的灰度不变。在肺图像的配准中，也需假设在呼吸过程中肺部图像的灰度值不随时间发生改变。该假设对于肺部以外的体元是完全成立的，但对于受激发空气影响致使密度发生改变的肺而言，灰度不变假设理论并不完全成立［2］。激发的空气使整个肺部的密度减少，肺的底部比顶部的密度改变更为明显，这种效应对配准精度尤其对靠近膈肌部位的配准会产生显著影响。二是由于肺部纹理干扰、心脏搏动、肺呼吸运动导致的局部大形变等因素的影响，肺图像的配准较易出现局部误配准或陷入局部极值。

为了减少灰度不均的影响，Sarrut等采用了一种肺密度校正的预处理方法，以提高肺部图像配准的精确性［2］。Yin等考虑到呼吸运动时肺组织密度的变化，提出了一种新的相似性测度［3］，称为平方组织体积不同（The sum of squared tissue volume different，SSTVD），将灰度变化与肺体积变化联系起来，设定肺组织密度与局部体积成一定反比，以提高配准精度。类似的，Gorbunova等也提出了相似的思想来提高肺配准精度［4］。Castillo等提出了结合块匹配和L1优化的约束B-spline肺图像配准方法［5］，以处理形变较大而陷入局部极值的问题。但肺图像配准精度的提高，仍需要继续深入研究。

本研究中，笔者提出了基于学习预测的肺4DCT图像配准方法。基于学习的思想在图像超分辨率重建［6］、图像分割［7］等方面得到了成功应用。在本研究中，由于呼吸运动的相似性，笔者们利用肺4D-CT图像的多相位特点，提出一种基于自身数据的逐块预测初始形变的方法，利用多维支持向量回归机（multi-dimensional support vector regressor，MSVR），预测待配准图像配准至参考图像的初始形变场，得到中间图像。相比初始待配准图像，此中间图像与参考图像更相似。而后，再分别用已有配准算法配准中间图像至参考图像，实现图像的最终配准。实验结果表明，与常用配准算法 Active Demons和Spectral Log-Demons［8］相比，本方法在视觉和量化方面都能获得更好的结果。

1 方法

1.1 基于回归预测的配准框架

回归预测的核心思想在于基于已知图像表观和对应形变场的样本集，学习训练一个非线性回归模型。而后利用该模型，预测新图像的初始形变。

基于回归预测的图像配准框架如图1所示。对于肺 4D-CT 数据I（I0，I1，I2，…，In），n＝9，其中Ii表示每个相位图像。设I0为参考图像，其余各相位为待配准图像。

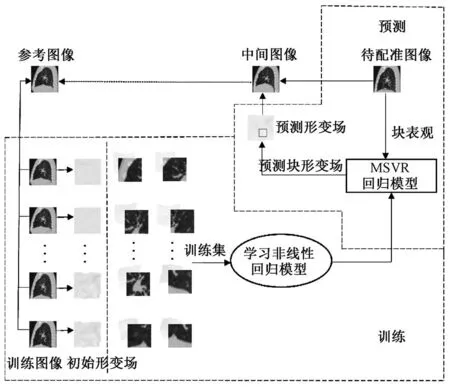
图1 回归预测配准框架Fig.1 Framework of regression prediction registration

以配准In为例，详细说明训练集的构建以及配准过程。配准过程主要可分为两个部分，训练过程与测试过程。

训练过程：用初始算法将I1，I2，…，In-1作为训练样本，分别配准至参考图像I0，得到每个训练样本图像对应于参考图像的形变场。之后将训练图像与其对应形变场分块构建训练集，利用MSVR学习图像块表观与形变场之间的非线性回归模型，即表观-形变回归模型。

预测过程：基于训练过程学习到的回归模型，根据待配准图像的表观，逐块预测出待配准图像In的块形变场，拼接整合得到初始形变场；再根据初始形变场，得到与待配准图像相对应的中间图像；最后利用已有配准算法，细化配准中间图像与参考图像。

获得In的形变场后，将In及其形变场放入训练集，以I1，I2，…，In-2，In作为训练集，重新预测配准In-1。如此循环，直至完成所有相位图像的配准。

由于回归预测得到的中间图像与参考图像之间的相似度更高，局部形变小于待配准图像与参考图像之间的形变，因此细化配准的效果将优于直接配准的效果，尤其对于待配准图像与参考图像之间形变较大的情况，效果提高显著。

1.2 图像表观-形变场回归模型

本研究以分块的图像和对应形变场作为训练集，采用多维支持向量回归机（MSVR）建立回归模型求解回归参数，以下详细介绍方法。

1.2.1 图像及形变场分块

首先配准各训练相位图像至参考图像，得到各自对应的形变场。由于对整幅图像进行处理时，存在维数太高、样本数目少以及局部细节［9］丢失等问题，且肺部图像局部结构差异比较大，因此本研究采用分块策略，将图像及其形变场分块之后作为训练集。本研究采用由左至右、从上到下的扫描式重叠方法分块［10］。利用图像块灰度表观作为输入、块形变场作为输出，构建基于多维支持向量回归机的非线性模型。

1.2.2 多维支持向量回归机

表观-形变回归模型是利用训练集中已知图像块表观和形变学习一种非线性映射函数，有

式中，X是输入图像块的表观，即图像块像素灰度，Y是输出图像块所对应的像素形变场。

本研究利用多维支持向量回归机（MSVR），求解该回归问题［11-12］。

MSVR是一种稀疏核机并且能够建模一个高维的非线性映射函数，它能够同时且独立地预测每个输出维度，使得空间相关性得到充分利用［7］。

MSVR目的在于学习以下回归函数，即

式中，φ(X)：Rm→Rh是一种非线性映射，从m维映射到更高维h空间。

从已知训练数据样本D＝ ｛(Xi，Yi)｜i＝ 1，2，．．．，n｝中，求解该回归函数主要的最优化参数W＝［w1，w2，．．．，wl］T和b＝［b1，b2，．．．，bl］T。其中，X∈Rm是图像各像素点灰度输入，Y∈Rl是图像各像素点对应形变输出，n为训练样本个数。

通过下述最优化问题求解W和b，得

W的最优解是训练样本在高维特征空间的一种线性组合［14］，即

结合式（3）～（5），通过迭代变权最小二乘法（IRWLS）［15］，可求得最佳W。求解得到之后，对于一个新的图像块表观的输入X，可由

求得其形变场。其中，K(Xi，X)＝φT(Xi)φ(X)是一个核函数，代表一个新的测试样本X与训练样本Xi在特征空间φ的点积。

核函数可以解决特征映射至高维空间时出现维数灾难问题，一旦明确了核函数，就无需知道映射φ的具体形式了，避免了在高维空间的计算［13］。几种常用的核函数是：高斯径向基函数、线性核函数、多项式核函数和Sigmoid核函数等。

本研究所选用的是线性核函数K(Xi，X)＝〈Xi，X〉，〈Xi，X〉 表示Xi和X的点积。线性核函数的参数较少，计算简单。实验表明，线性核函数能满足本研究需求，取得了较好的实验结果。

1.3 预测初始形变场

得到回归模型之后，即可预测出待配准图像的初始形变场，从而得到与之对应的中间图像。

将待配准相位图像分块，块表观作为输入，预测出图像块形变场，拼接为整幅图像形变场，对整个形变场进行高斯平滑，得到最终预测初始形变场以及中间图像。图2给出了图像利用 Active Demons形变预测的典型例子，其中（a）、（b）分别为参考图像和待配准图像，（c）为（b）中方框内图像的放大显示，（d）为根据图像整体预测形变场构建的中间图像，（e）为（c）由 ActiveDemons配准得到的块形变场，（f）为通过回归预测得到的（c）的预测块形变场，（g）为（b）由ActiveDemons配准得到的整体图像形变场，（h）为通过连续块预测后整合而成的整体图像预测形变场。可以看到，由预测形变场得到的中间图像与参考图像在整体上更加接近，尤其在运动幅度比较大的肺下部区域。

图2 预测初始形变场以及中间图像。（a）参考图像；（b）待配准图像；（c）（b）中方框内图像块的放大显示；（d）中间图像；（e）（c）中图像块的 Active Demons配准块形变场；（f）（c）中图像块的回归预测块形变场；（g）Active Demons配准形变场；（h）回归预测配准形变场Fig.2 The initial deformation field and the intermediate image.（a）The reference image；（b）The floating image；（c）The enlarged image in block areas of（b）；（d）The intermediate image；（e）The block deformation field by Active Demons algorithm in（c）；（f）The block deformation field by regression-based method in（c）；（g）The deformation field by Active Demons algorithm；（h）The deformation field by regression-based method；

得到中间图像之后，只需要配准形变较小的中间图像与参考图像，这就避免了由于待配准图像与参考图像之间形变较大、配准容易陷入局部极值的问题。

1.4 图像配准结果量化评价

实验数据是由DIR实验室提供的公共可用的肺4D-CT数据集［16］。该数据集包含多组肺4D-CT数据，每组数据包含了10个呼吸相位。数据层内的体素尺寸范围为0.97 mm×0.97 mm～1.16 mm×1.16 mm，层间间距为2.5 mm。分别用 Active Demons算法、Spectral Log-Demons算法以及本研究所用的回归预测算法进行配准，并进行比较分析。

采用均方误差平方和（SSD）以及相关系数（CC），作为比较传统的Active Demons算法、Spectral Log-Demons算法与本研究提出的回归预测配准方法的量化评价指标。量化评价指标分别为

式中：N为图像像素个数的总数；Fi为参考图像，为参考图像像素灰度的平均值；Ti为配准后图像，为配准后图像像素灰度的平均值。

SSD值越小，说明图像相似程度越高；CC值越大，说明两幅图像相关性越大，配准效果越好。

2 实验结果

2.1 视觉评价

图3、4给出了典型的 Active Demons、Spectral Log-Demons以及本算法配准的实验结果。从中可以看出，相比直接配准浮动图像至参考图像，所提出的方法获得了更好的配准结果，由差分图像可进一步验证了这一点。

图3 Active Demons算法、Spectral Log-Demons与回归预测算法配准实验结果。（a）参考图像；（b）待配准图像；（c）Active Demons配准图像；（d）Active Demons配准差分图像；（e）Spectral Log-Demons配准图像；（f）Spectral Log-Demons配准差分图像；（g）回归预测配准图像；（h）回归预测配准差分图像Fig.3 The view of registration results by use of different methods.（a）The reference image；（b）The floating image；（c）The result of registration by Active Demons algorithm；（d）The difference image by Active Demons algorithm；（e）The result of registration by Spectral Log-Demons；（f）The difference image by Spectral Log-Demons；（g）The result of registration by regression prediction method；（h）The difference image by regression prediction method

图4 Active Demons算法、Spectral Log-Demons与回归预测算法配准实验结果（图像排列方式与图3相同）Fig.4 The view of registration results by use of different methods（The arrangement is same as Fig.3）

2.2 量化评价

表1针对DIR数据集其中的8组数据，分别使用Active Demons算法、Spectral Log-Demons算法、本算法进行配准，之后计算各相位的平均SSD。为了使评价结果更直观，表1给出了二者与本算法之间的SSD减少百分比。本方法的平均均方误差和明显低于传统Active Demons和Spectral Log-Demons算法，说明本方法的配准更为准确。

将表1中3种不同方法的平均SSD进行非参数独立样本的Kruskal-Wallis检验，P＝0.004＜0.05，按α＝0.05的检验水平，差异具有显著性，可认为本算法的SSD低于Active Demons算法和Spectral Log-Demons算法。

图5是由 Active Demons算法、Spectral Log-Demons算法与本算法配准后图像与模板图像之间相关系数的柱状图。可以看出，本研究方法配准得到的相关系数比Active Demons算法以及Spectral Log-Demons算法配准得到的相关系数值大，表明配准后图像与参考图像的相关性增强。

同时，将上述3种不同方法的平均CC进行非参数独立样本的 Kruskal-Wallis检验，P＝0.01＜0.05，按α＝0.05的检验水平，差异具有显著性，可认为本算法的 CC高于 Active Demons和 Spectral Log-Demons算法。

表1 Active Demons配准、Spectral Log-Demons与回归预测配准的平均SSDTab.1 The average SSD by Active Demons registration，Spectral Log-Demons and our proposed methods

图5 Active Demons配准、Spectral Log-Demons与回归预测配准的平均相关系数Fig.5 The average CC by Active Demons registration，Spectral Log-Demons and our proposed methods

3 讨论和结论

本研究对于灰度均匀性差、局部形变大的肺部4D-CT图像配准问题，提出了一种提高配准精度的算法。先利用多维支持向量回归机，建立图像表观与图像形变场之间的回归模型；再通过逐块预测的方法，得到待配准图像的初始形变场。该方法的关键在于利用了不同相位的图像信息来预测待配准图像的初始形变场，减少了待配准图像与参考图像之间的显著形变，提高了配准准确性。

肺部图像的配准，是对肺疾病、肺运动等进行纵向分析的辅助手段之一［4］。由于主客观原因的影响，不同诊断治疗时段甚至于不同呼吸时刻获得的肺部图像，都可能存在影响肺部疾病分析的形变。由于肺部图像本身的特殊性，精确配准肺部图像始终是研究的热点方向。本研究提出了一种基于预测的肺4D-CT多相位图像配准方法，实验表明，该方法能对肺4D-CT的配准取得较好的效果，同时也为需要进行纵向分析的其他医学图像配准（如大脑追踪研究等）提供了参考手段。

本研究所提出的算法时间开销主要包含4个部分：训练集构建配准过程，即使用初始算法配准训练相位图像至参考图像所用时间；训练过程，即利用训练集学习回归模型参数；预测过程，即预测初始形变场所用时间；精配准时间，即完成细化配准所需时间。其中，训练过程、预测过程和精配准过程为较一般直接配准方法所增加的时间开销。训练过程所需时间消耗为51.84 s，所需预测时间为224.28 s，而精配准时间约为初始配准所需时间的53.10%。这是由于经过预测后，配准形变较小，故精配准收敛速度有所提高。

值得一提的是，在对各相位进行训练和预测过程中，只需在原有的训练集中进行图像和形变场的更替，无需再进行配准过程，这在很大程度上节省了本方法的时间开销。在下一步工作中，拟探索更加快速、优质的训练和预测方法。同时，在肺部图像中，肺内部与肋骨之间存在不连续的滑动［17］，这在一定程度上影响了肺部图像的配准。而在许多临床应用研究中，通常只需要对肺内部的结构进行研究，因此考虑先将肺部图像进行分割，再进行更准确的配准。

实验结果表明，本研究提出的基于回归预测的配准方法能有效实现肺部图像的配准，增强结构细节的配准精确性，在视觉和量化比较方面均优于传统的 Active Demons和 Spectral Log-Demons算法。肺部4D-CT在肺癌的个体化治疗中发挥着重要的作用，而肺部图像的配准，对于肺的运动估计、肺肿瘤的定位和放射治疗的精准性有实际意义。本研究的方法，为配准肺部4D-CT图像提供了一种可能的新方案。

［1］ Sluimer I，Prokop M，Van GB.Toward automated segmentation of the pathological lung in CT ［J］.IEEE Transactions on Medical Imaging，2005，24（8）：1025-1038.

［2］ Sarrut D，Boldea V，Miguet S，et al.Simulation of fourdimensional CT images from deformable registration between inhale and exhale breath-hoet al.ld CT scans ［J］.Medical Physics，2006，33（3）：605-617.

［3］ Yin Y，Hoffman EA，Lin CL，et al.Mass preserving nonrigid registration of CT lung images using cubic B-spline ［J］.Medical Physics，2009，36（9）：4213-4222.

［4］ Gorbunova V，Sporring J，Lo p，Loeve M，et al.Mass preserving image registration for lung CT ［J］.Medical Image Analysis，2012，16（4）：786-795

［5］ Castillo E，Castillo R，Fuentes D，et al.Computing global minimizers to a constrained B-spline image registration problem from optimal L1 perturbations to block match data ［J］.Medical Physics，2014，41（4）：041904-041904.

［6］ Yang J，Wright J，Huang TS，et al.Image super-resolution via sparserepresentation ［J］.IEEE Transactions on Image Processing，2010，19（11）：2861-2873.

［7］ Wang Z，Zhen X，Tay KY，et al.Regression segmentation for M3 spinal images ［J］.IEEE Transactions on Medical Imaging，2014，34（8）：1640-1648.

［8］ Lombaert H，Grady L，Pennec X，et al.Spectral Log-Demons：Diffeomorphic Image Registration with Very Large Defoemation［J］.International Journal of Computer Vision，2014，107（3）：254-271.

［9］ Kim M，Wu G，Wang Q，et al.Improved image registration by sparse patch-based deformation estimation ［J］.NeuroImage，2015，105：257-268.

［10］ Wang T，Cao L，Yang W，et al.Adaptive patch-based POCS approach for super resolution reconstruction of 4D-CT lung data［J］.Physics in Medicine and Biology，2015，60（15）：5939-5954.

［11］ Rez-Cruz F，Camps-Valls G，Soria-Olivas E，et al.Multidimensional function approximation and regression estimation［C］ //International Conference on Artificial Neural Networks.Madrid：CANN，2002：757-762.

［12］ Sanchez-Fernandez M，De-Prado-Cumplido M，Arenas-Garcia J，et al.SVM multiregression for nonlinear channel estimation in multiple-input multiple-output systems ［J］.IEEE Transactions on Signal Processing，2004，52（8）：2298-2307.

［13］ 张学工.模式识别［M］.3版.北京：清华大学出版社，2010：109，114-115.

［14］ Scholkopf B，Somla A，Learning with Kernels［M］Cambridges：MIT Press，2002.

［15］ Perez-Cruz F，Alarcon-Diana P，Navia-Vazquez A，et al.Fast training of support vector classifiers ［J］.Advances in Neural Information Processing Systems，2001：1849-1870.

［16］ Castillo E，Castillo R，Guerra R，et al.A framework for evaluation of deformable image registration spatial accuracy using large landmark point sets ［J］.Physics in Medicine and Biology，2009，54（7）：1849-1870.

［17］ Schmidt-Richberg A，Werner R，Handels H，et al.Estimation of slipping organ motion by registration with direction-dependent regularization ［J］.Medical Image Analysis，2012，16（1）：150-159.

Lung 4D-CT Image Registration Based on Regression Prediction

Liu Yueliang1，2Fang Shiting1，2Zhang Yu1，2∗

1（School of Biomedical Engineering，Southern Medical University，Guangzhou510515，China）

2（Guangdong Provincial Key Laboratory of Medical Image Processing，Southern Medical University，Guangzhou510515，China）

To improve the low accuracy of lung 4D-CT image registration due to intensity inhomogeneity and large local deformation，a regression-based method for predicting initial deformation is presented.The core idea of this method is that the image information of different phase corresponding to the floating image is used to predict initialize deformation field.Firstly，the common registration algorithmis used to register the different phase images to the reference image to get the corresponding deformation field.Then，the image and the corresponding deformation field are divided into patches to build training set.Multi-dimensional support vector regressor is used to learn a regression model with respect to the correlation between patch appearances and their respective deformations.The floating image is then input into the regression model to achieve the initial deformation field prediction，which is used to construct intermediate image.Finally，the registration of intermediate image and reference image are refined.The experimental results show that the proposed method can effectively register lung 4D-CT images.A public dataset provided by the DIR-lab at the University of Texas M.D.Anderson Cancer Center（Houston，TX）was employed to evaluate the proposed method.Quantitative evaluation results indicate that the proposed method significantly decreases SSD（18.97±5.75，P＜0.05）compared with Active Demons algorithm（49.34±23.92）and Spectral Log-Demons algorithm（31.81±15.09），significantly increases CC（0.980 ± 0.006，P＜0.05）compared with Active Demons algorithm（0.952±0.022）and Spectral Log-Demons algorithm（0.967 ±0.015）.Qualitative evaluation results also show that our approach can yield superior registration performance.

lung 4D-CT；image registration；deformation prediction；multi-dimensional support vector regressor

R318 文献标志码：A 文章编号：0258-8021（2017）05-0513-07

10.3969 /j.issn.0258-8021.2017.05.001

2016-12-09，录用日期：2017-06-04

国家自然科学基金（61671230）；广东省科技计划项目（2017A020211012）；广州市科技计划项目（201607010097）

∗通信作者（Corresponding author），E-mail：yuzhang@smu.edu.cn