航空薄壁件原位检测与补偿加工方法研究

王 刚，童 刚，毛金城，李文龙

（华中科技大学机械科学与工程学院，湖北 武汉430074）

航空薄壁件原位检测与补偿加工方法研究

王 刚，童 刚，毛金城，李文龙

（华中科技大学机械科学与工程学院，湖北 武汉430074）

航空结构件、航空叶片等薄壁零件是航空制造的关键零件，具有若刚性、材料难加工、工艺优化不足等特点，其加工精度难以控制。针对航空薄壁零件的在机测量与误差补偿方法展开研究，针对规则航空薄壁零件提出均值误差补偿方法，并在此方法的基础上延伸为针对自由曲面的分段误差补偿方法，最后对航空叶片进行了数控加工、原位检测及补偿加工实验，实验结果表明，补偿前后误差区间从0.15 mm～0.35 mm缩小到了-0.04 mm～0.06 mm，验证了分段误差补偿方法在加工几何偏差控制上的效果。

航空；薄壁零件；在机测量；补偿加工

航空薄壁零件广泛应用于飞行器的各个部件中，其精密加工技术是提高航空产品加工精度和效率的关键。这类零件加工过程中精度难以控制，主要体现在：（1）具有弱刚性，一般为悬臂结构，壁厚很薄，加工中易引起弹性变形，导致航空薄壁件加工偏差难以控制；（2）材料难加工，该类零件通常采用钛合金、高温合金、高强度铝合金等难加工材料，钛加工过程中活性高易产生硬脆氧化层加剧刀具磨损；（3）工艺优化不足。加工效率较低，对钛合金、超硬铝、高温合金等难加工材料的加工，由于缺乏先进加工工艺的指导，目前使用的加工方法普遍比较保守，提高了加工的时间成本。针对以上问题，如何预测和抑制零件加工变形，并对工件变形进行补偿一直是学术界研究的热点。

切削变形是加工过程中的不可避免的难题，在变形机理上，Nachbagauer提出利用数值模拟的思想，建立切削力的理论模型，工件在切削力的作用下，产生弹性变形，使得刀具无法切削到理论的位置，借助有限元软件实现对弹性变形的模拟[1]。Hlandt通过对材料的性能进行深度分析，并通过大量试验，分析不同材料的工件在加工过程中的变形趋势[2]。金超认为工件在切削热的影响下会产生塑性变形，并在试验中安装热传感器，建立切削热-变形的模型[3]。学术界对变形的机理研究各有特点和侧重，但主要的还是集中在对“力—变形”这一系统进行研究[4-6]。加工过程中出现的种种因素都将对薄壁零件最终的加工质量造成影响，同时各因素相互耦合，简单的提取一两项因素进行深度分析都将面临巨大的工作量。为了提高薄壁零件的加工精度，国内外学者从不同的角度对工艺系统进行改造和优化，干预变形过程。西北工业大学的王婧超等通过对模型结构优化设计，合理的结构能够抵御一部分刀具的作用力，在不增加零件的厚度条件下提升零件的刚性，从而减小弹性变形[7]。An等研究切削速度对薄壁变形的影响，在高速切削条件下，避开薄壁零件的共振频率，单次切削能有效减少刀具与工件表面的作用时间，减少切削冲量，提高效率的同时减小变形[8，9]。北京航空航天大学李忠群等通过建立切削的有限元系统，输入适当的边界条件，仿真整个切削过程，根据仿真结果预测真实切削发生变形，找出引起变形的主要因子，并在实际加工中对其削弱[10，11]；陈蔚芳等人开发了一套加工变形快速仿真平台，通过对影响加工变形的因素进行集成化仿真，得到优化的加工参数，提高加工质量[12]。

当前的研究在误差变形预测上主要利用有限元仿真的手段，这是一个成本低效率高的方法，然而精确的边界条件获取是一个难题，仿真的结果并不能直接用于指导补偿加工。原位检测技术是一种随着机床和测量技术发展而兴起的技术，是相对于典型三坐标测量机使用的离线测量方法的一种测量方案[13]。相对于以上传统测量手段及方案，原位检测具有以下优势和特点：

（1）测量自动化，无需对工件进行二次装夹。直接利用数控机床本体和机床测头即可完成三坐标测量机的测量过程，特别是对大型工件或者精密零件来说，为了进行高精度的测量来回转运的成本太高，而原位检测技术正是弥补了这一短板。

（2）加工-测量自动切换。将测量的定位精度提升到了微米级深知亚微米级，在高精密的机床上使用可以和普通的三坐标测量机相媲美[14]，在加工过程中随时自动切换到测量模式，对工件进行快速测量，为精密零件的质量控制带来契机。

（3）模型重建。引入测量坐标系，定义测量坐标系与加工坐标系相对位置关系，由于数控加工中加工坐标系与CAD模型坐标系具有精密的联系，因而可将三个坐标系进行统一起来，建立CAD、工件、误差模型的关联，进行所需的数据分析。

补偿加工技术仅过了多年的发展，对提升加工质量的提升取得了很多重要理论和成果[15-17]，但在实际应用上还存在一些不完善之处。

本文针对以上航空薄壁件加工的几何变形的背景，对薄壁件变形量的原位检测和补偿加工两个方面作为研究的出发点，探索出一种能够适用于航空薄壁件原位检测与补偿方案，达到能随时量化加工过程中薄壁件的加工偏差，并对偏差施以补偿，最终提高薄壁件的加工精度和效率的目的，最后通过实验验证了该方法的有效性。

1 薄壁件补偿策略

1.1 一般规则薄壁件加工代码均值偏差补偿

首先考虑航空领域最为常见的规则特征的薄壁件，如平面、规则曲面零件，其加工后变形规律为整体向一个方向发生了倾斜或者偏移，如图1所示，通常刚性弱的一段变形量大于刚性好的一端，即悬臂结构的根部到顶部偏差逐步扩大化，测点的分布如图2所示。

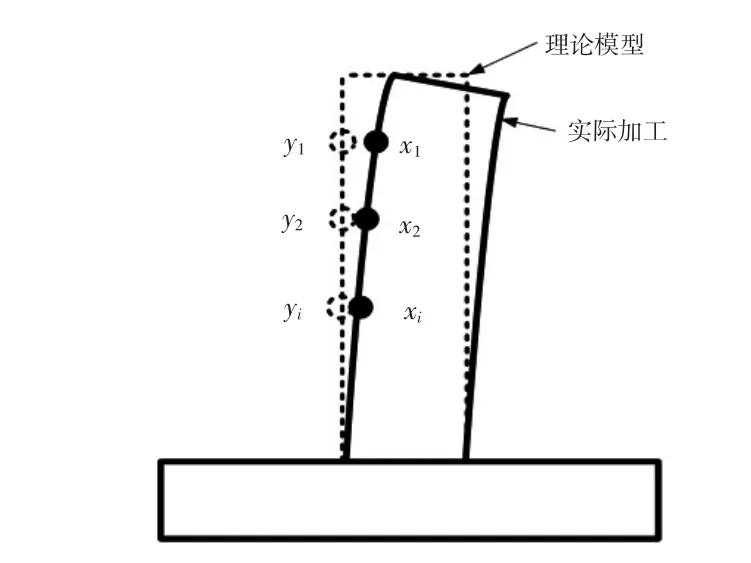
图1 规则特征变形示意图

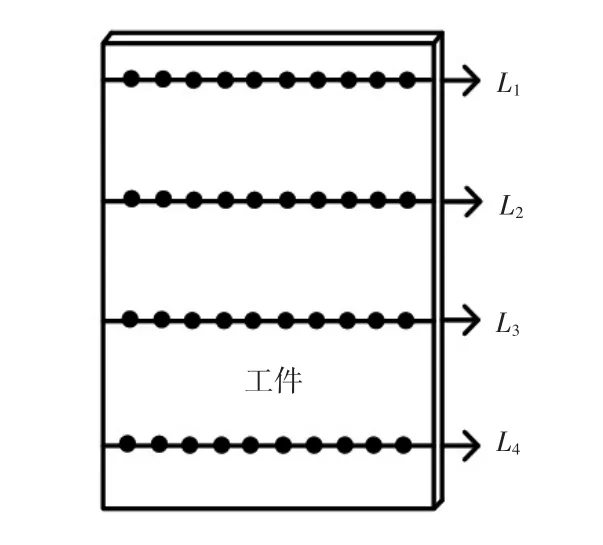
图2 测点的分部

在图1中，yi是理论点位置，xi是实际加工测量得到的对应点的位置，对于薄壁平面件及规则曲面件，加工后产生的偏差用公式表达为：

式中向量ei为理论点与实际点的偏差，对图2的测点的数据进行统计排列，得到图3中所示的折线，可以看出整个测点的误差分布在一个偏差带的范围内。

图3 规则薄壁件分布规律

根据实际的分析，偏差分布带ε与余量δ的比值为：

因此可以认为偏差的分布在一个相对较窄的区域，在考虑到机床的误差的条件下，可以将总体分布的偏差均值σ作为评价偏差的标准，记作：

根据所有的点均值偏差，修改精加工的数控代码，使新的加工路径能够抵消大部分综合误差引起的变形。由于半精加工与精加工选用完全相同的加工工艺参数以及同一把刀具，在切削量较小的条件小，可以忽略刀具微小磨损对切削变形的影响，同时由于半精加工、精加工的切削量减小，工件薄壁厚度的变化对工件刚度的影响也可以忽略，通过实际的加工试验已经得到验证，可以得出在精加工中工件变形的趋势及变形量将与半精加工趋近相同的结论，因此将半精加工的变形量作为精加工理论补偿量比较合适的。

对于理想的补偿加工，根据精确的测量半精加工后的偏差，然后对精加工时施加一个反向的偏差的，使得精加工的走刀轨迹能够补偿掉半精加工的偏差，如图4所示的理想补偿方法，根据上述分析结果，实际操作中简单薄壁件的补偿如图5所示。

图4 理想偏差补偿原理图

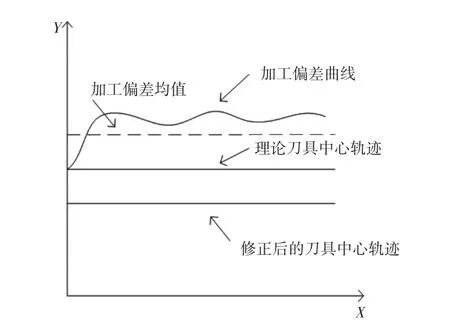
图5 实际偏差补偿原理图

均值偏差策略思想就是将原始的精加工刀具轨迹在发向上平移一个值，如图6到图7的变化，而以均值偏差作为补偿值的参考值，在此基础上引入一个补偿系数λ，不同的材料和特征对应补偿系数λ不尽相同，进行N次迭代可以得出该种特征下的最优。原始的精加工刀具轨迹和补偿后的刀具轨迹，对比可知，补偿后对原始的轨迹在进给部分沿着法相方向作了一个整体平移，进刀退刀部分采用斜线过渡，避免加工过程中轨迹的突变产生较大的震动，降低加工的精度。

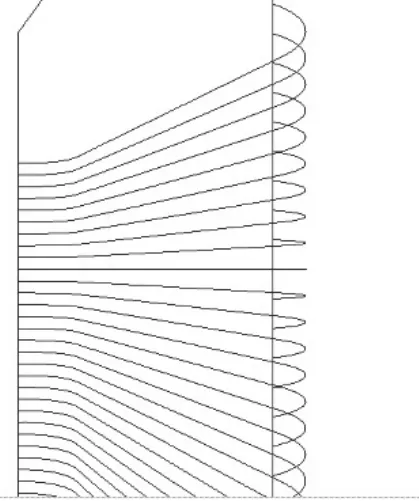
图6 原始精加工刀具轨迹

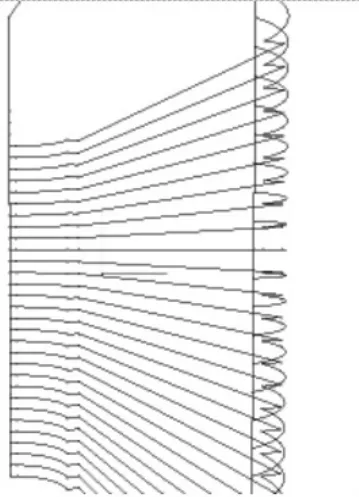
图7 补偿后精加工刀具轨迹

1.2 自由曲面薄壁件加工代码分段补偿

相对于1.1节中的均值偏差补偿策略适用于规则的平面或曲面，本节的分段补偿方法则适用于对自由曲面的情况，对于自由曲面薄壁件，由于各个部位及各个点的偏差分布没有规律可循，如图8所示为自由曲面加工后进行的测量偏差分布。直接用均值进行补偿可能会导致局部严重的过切或欠切，因此需要以规则薄壁件的补偿方法为基础，将每一条轨迹离散为直线段或圆弧段，进行分段修改，达到精确的控制。

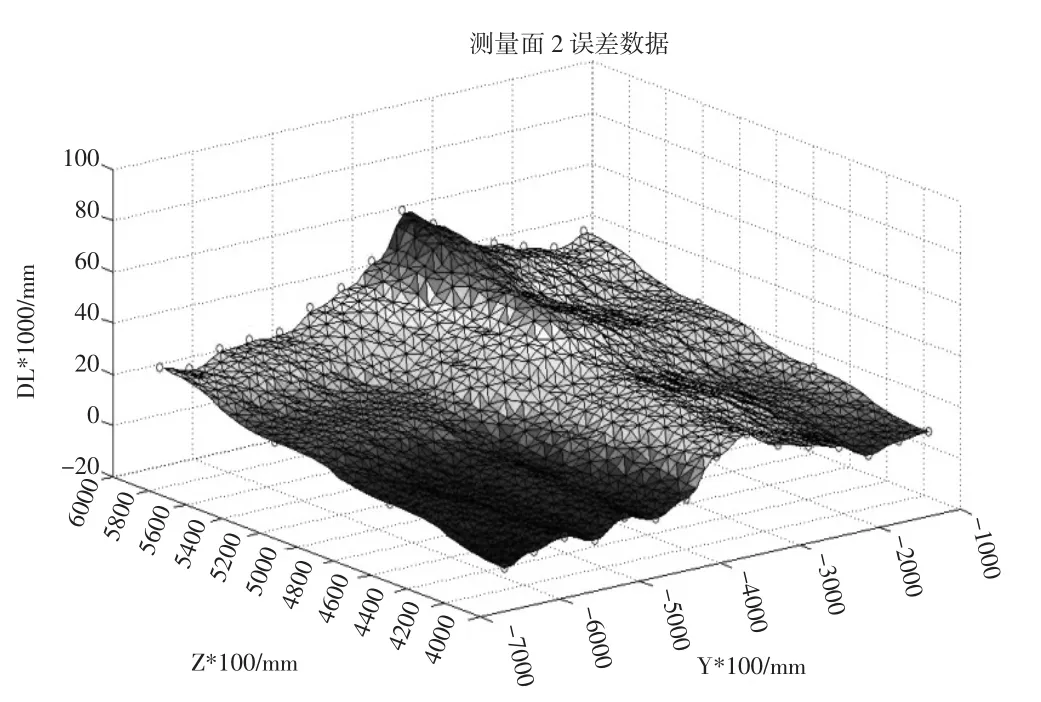
图8 自由曲面偏差分布

实现分段补偿的核心之一就是能对NC代码进行快捷的操作和修改，本文采用的是海德汉数控系统的机床，编码系统不同于常见的G代码系列，因此程序必须识别各项指令的含义，才能对其精确的增删，海德汉系统的代码定义的命令符为L、C、CC等。

对加工后的数据偏差进行分析，一般存在两种结果，以正偏差代表的欠切和负偏差代表的过切，侧铣加工过程中只需要对刀具进行平移即可实现刀轨的补偿。对于直线进给，如图9所示，点1至点2为直线进给，0-1段和2段之后为进、退刀的非进给行程，不对工件切削作贡献，只是作为导轨之间的过渡和避障。

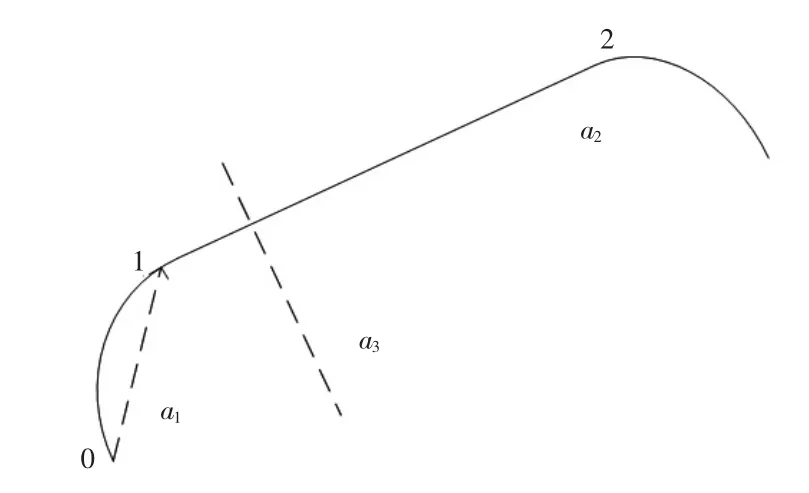
图9 单刀直线运动轨迹图

设 0-1段直线与X轴向量角为 a1，1-2段为a2，1-2段的垂线为a3，加工中实际的走刀轨迹0-1段的角度为a，即根据a的情况对a1进行修改就可对平面的加工轨迹平移到想要的补偿位置，为了避免估计的轨迹突变给机床系统带来的加速度和跃度过大，可以在之间插入余弦线段进行过渡，避免冲击带来加工误差。据此得到切入切出点的补偿后的坐标值，原始轨迹点分别（x1，y1），补偿后的点位（x1，′），σ为偏差均值，得到：

对于轨迹是圆弧的情况，如图10所示，0-1、2-3段为进出刀行程，1-2为进给行程，设0-1段与X轴夹角为β，补偿后的夹角为β′，新点的法向方向为βi（i=1，2）.

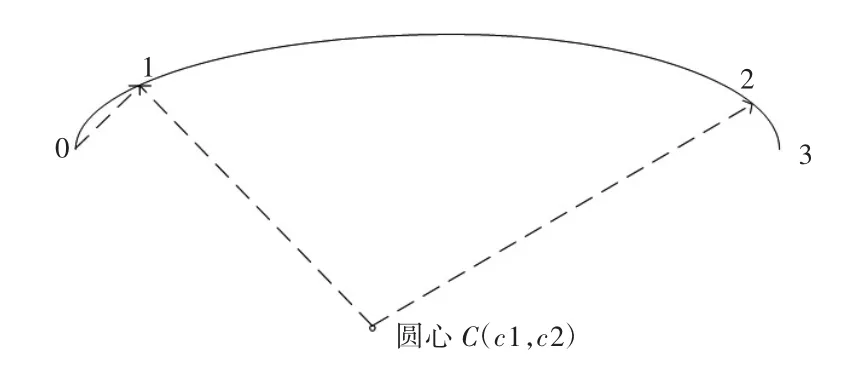
图10 圆弧运动单刀轨迹图

圆弧1-2段均值误差值为σ，修改后的坐标为

根据上述的推导，在自由曲面加工中通常使用小线段或者小圆弧的逼近方法，因此获得加工表面的加工偏差后，使用移动最小二乘法拟合和多项式差值，设置差值精度取值与补偿的精细程度在同一个量级，将离散点的偏差扩充到整个加工平面。如图11和图12所示的补偿原理和补偿思路，通过离散点补偿精加工轨迹。

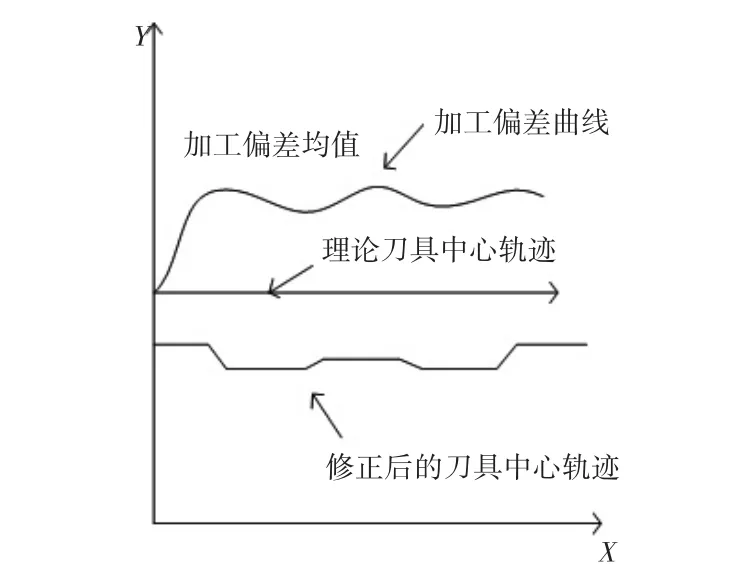
图11 分段偏差补偿原理图

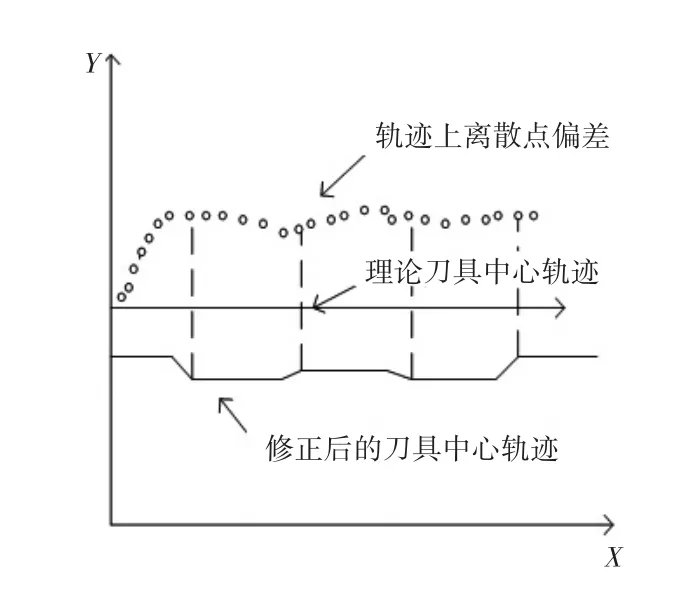
图12 分段偏差补偿思路

根据上面的方法，使用移动最小二乘法评估每一条线段上的偏差量，然后进行多项式插值，对每一条小段进行修改，如图13所示的原始精加工代码和14所示的修正后的精加工代码，即可对整个自由曲面进行补偿加工。

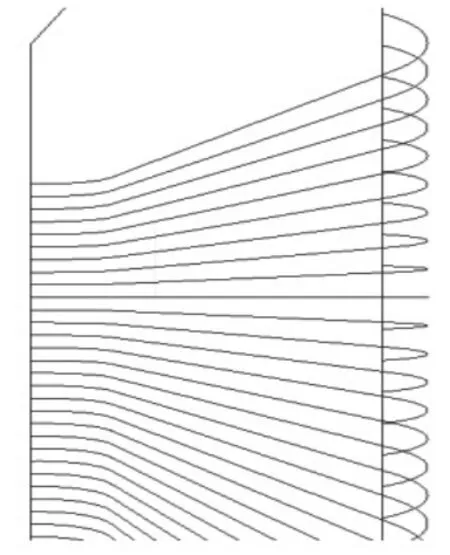
图13 原精加工刀具轨迹

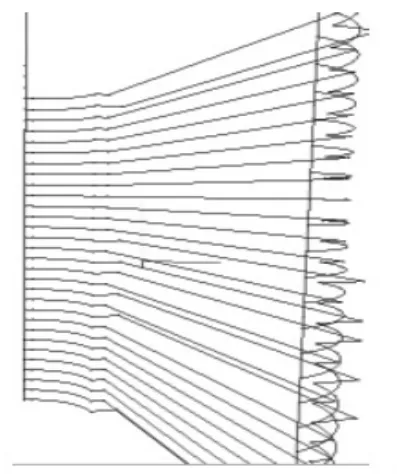
图14 修改后精加工刀具轨迹

2 薄壁件加工-补偿实验

2.1 实验条件

下面以航空薄壁件的典型零件航空叶片为例，进行在机测量与补偿加工实验。

（1）机床采用瑞士米克朗UCP800Duro五轴联动高速加工中心，搭载heidenhain iTNC530M，机床重复定位精度0.004 mm.

（2）毛坯：薄壁叶片毛坯选用航空铝合金7075板材，毛坯尺寸为250 mm×100 mm×40 mm，其中150 mm用于加工叶片部分，50 mm为榫头，剩余的用于夹持，如图15所示。

图15 毛坯及夹具尺寸

（3）定位装夹方式：由于实验主要目的是对叶片自由曲面特征的加工过程中的综合偏差变形进行补偿效果验证，采用普通的通用夹具即可，如图15所示，没有添加辅助工装。

（4）刀具、测头选用：本实验粗加工选用平底钨钢刀，直径10 mm，刀长150 mm，刃长50 mm，3刃；半精加工和精加工使用钨钢球头刀，半径5 mm，刀长75 mm，刃长25 mm，以及加工榫头、圆角的2.5 mm半径球头刀。原位检测测头选用雷尼绍RMP40测头，重复定位精度0.001 mm.刀具和测头物理参数如图16和图17所示所示。

图16 刀具物理参数

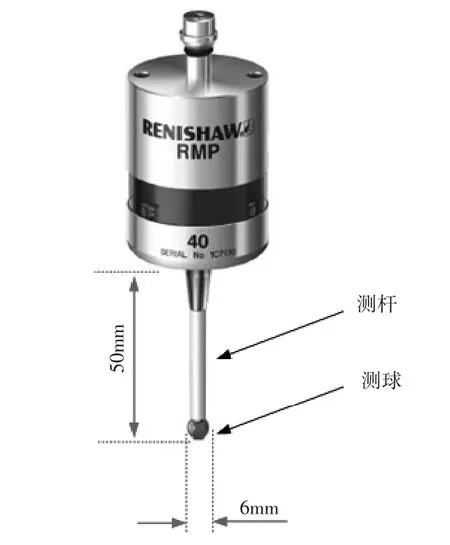
图17 测头物理参数

2.2 加工及在机测量实验

本文从实际质量要求及考虑工件毛坯出发，将加工阶段划分为粗加工-半精加工-精加工三个阶段，但又与传统的三个阶段有所区别，具体划分为：

（1）粗加工：完成传统粗加工-半精加工任务，去除绝大部分的余量，保证加工效率。

（2）半精加工：粗加工后进行半精加工，设计很小的切削量，为原位检测做准备。

（3）精加工：精加工设计成与半精加工完全相同的工艺参数并使用同样的刀具，尽可能的保留半精加工同样的变形趋势，使得补偿加工的规律能够得到应用。

为了验证补偿加工的效果，薄壁叶片既是实验组，也作为对照组，加工参数设计如表1所示，其中粗铣使用平底刀快速去除大部分毛坯余量，半精铣1使叶片加工到光整的表面，半精铣2相当于是带有余量的精铣，之后进行原位检测，对NC代码修正后，对叶片进行精铣工序，结束后再次进行原位检测，工艺过程及参数如表1所示。

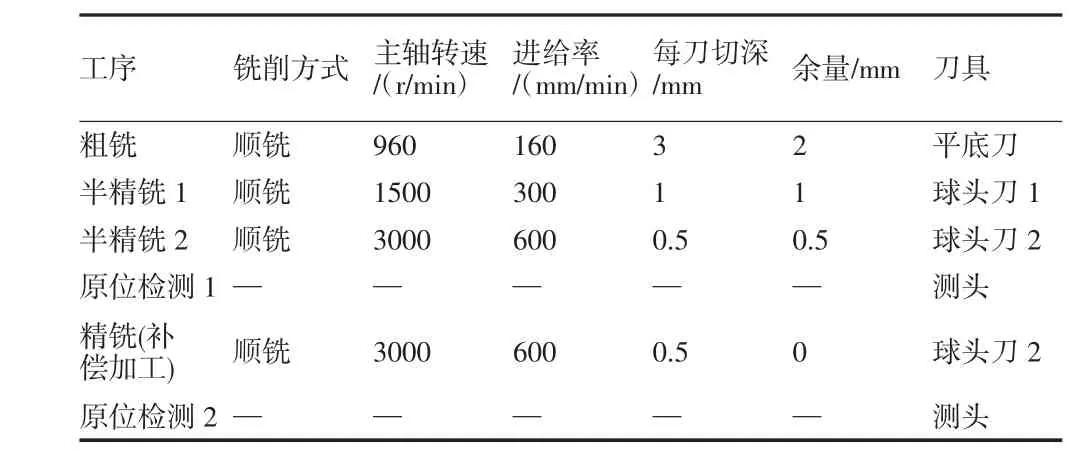
表1 加工参数

加工过程现场图片如图18至图21所示。

图18 五轴加工

图19 半精铣1后

图20 半精铣2后

图21 精铣后

原位检测规划及测量过程。分别在半精铣2和精铣后进行原位检测，测点分布如图22所示，叶盆、叶背各分布14×20=280测点，以此从叶顶到叶根，点集从1～20，每个点集14个点，测量过程如图23所示。

图22 测点分布

半精加工后测点数据分析。按照点集分布次序，统计结果如图24所示。

图24 半精加工后叶片偏差分布

从图中误差分布的情况可以得出以下结论：

（1）半精加工后叶片的整体加工变形较大，分布在0.15 mm～0.35 mm的误差区域内，主要由于工件刚性差且无辅助工装、加工参数没有作专门的优化以及其他所有误差因素综合引起，与前期加工偏差的经验数据相吻合。

（2）叶根到叶顶，变形误差逐渐扩大，顶部加工偏差接近0.35 mm，这部分主要由于顶部厚度为3 mm左右，薄壁结构十分明显，导致加工过程中“让刀”现象十分明显。

2.3 补偿加工结果分析

根据半精加工后的测量数据，运用逐行修改精加工数控代码的原理，将理论精加工代码和半精加工误差导入到自行编写的软件模块中，得出补偿加工的代码，如图25所示。

图25 精加工代码补偿

导出经过优化补偿的精加工代码后对叶片进行精加工，并进行原位检测终检，作为与半精加工的测量数据机型对比，如图26所示为精加工后原位检测中终检过程。

图26 叶片精加工后在线终检

根据测点的数据偏差信息绘制如图27偏差分布折线图。

图27 精加工后叶片偏差分布折线图

数据分布的规律可以得出以下结论：

（1）精加工的偏差分布整体上达到预期的补偿效果，从半精加工0.15 mm～0.35 mm的误差区间缩小到了-0.04 mm～0.06 mm的误差区间；

（2）精加工后的数据误差线条与半精加工后相比，光滑程度降低，数据走势规律性变弱，与补偿算法的优化程度有一定关系，为了控制整体的加工偏差，修改每一段加工程序，而相邻两行程序间的过渡与衔接需要进一步优化。

3 总结

本文针对航空薄壁零件的在机测量与补偿加工策略展开研究，提出了一种针对一般规则薄壁件的均值补偿方法，并在此方法的基础上延伸为针对自由曲面的分段误差补偿方法，对典型的自由曲面薄壁件即航空叶片进行了数控加工、原位检测及补偿加工实验，将半精加工后原位检测数据与误差补偿后精加工原位检测的偏差数据对比，实验结果表明，补偿前后误差区间从0.15 mm～0.35 mm缩小到了-0.04 mm～0.06 mm，验证了分段误差补偿方法在加工几何偏差控制上的效果，为其他类型的复杂薄壁零件的补偿加工提供参考。

[1]Nachbagauer K.State of the art of ANCF elements regarding geometric description，interpolation strategies，definition of e lastic forces，validation and the locking phenomenon in com parison with proposed beam finite elements[J].Archives of Computational Methods in Engineering，2014，21（3）：293-319.

[2]K nig W，Klinger M，Link R.Machining hard materials with geometrically defined cutting edges—field of applications and limitations[J].CIRP Annals-ManufacturingTechnology，1990，39（1）：61-64

[3]金 超.基于工况的数控加工热误差与切削振动预测方法研究[D].武汉：华中科技大学，2011

[4]Chaari F，Baccar W，Abbes M S，et al.Effect of spalling or tooth breakage on gearmesh stiffness and dynamic response of a one-stage spur gear transmission[J].European Journal of Mechanics-A/Solids，2008，27（4）：691-705

[5]Buc B，Buc D G.The influence of the specific cutting force and cross-sectional geometry of a chip on the cutting force in the process of circular rip-sawing[J].Holz als Roh-und Werkstoff，2002，60（2）：146-151.

[6]谭 刚.球头铣削切削力建模与加工表面形貌仿真研究[D].西安：西北工业大学，2007.

[7]王婧超.航空发动机三维单晶涡轮叶片的多学科设计优化[D].西安：西北工业大学，2007.

[8]An H P，Rui Z Y，Wang R F，et al.Research on cuttingtemperature field and distribution of heat rates among a work piece，cutter，and chip for high-speed cutting based on ana lytical and numerical methods[J].Strength of Materials，2014，46（2）：289-295.

[9]Tanaka Y，Ichimiya N，Onishi Y，et al.Structure and prop erties of Al–Ti–Si–N coatings prepared by the cathodic arc ion plating method for high speed cutting applications[J].Surface and Coatings Technology，2001，28（146）：215-221.

[10]李忠群.复杂切削条件高速铣削加工动力学建模、仿真与切削参数优化研究[D].北京：北京航空航天大学，2008.

[11]李志强.曲面的宽行数控加工理论研究及其在大型抛物面天线加工中的应用[D].北京：北京航空航天大学，2004.

[12]陈蔚芳，陈 华，楼佩煌，等.薄壁件加工变形控制快速仿真平台开发[J].计算机集成制造系统，2009，15（02）：321-327.

[13]Farrell G，Leung Y K.Innovative Online Assessment Using Confidence Measurement[J].Education and Information Technologies，2004，9（1）：5-19.

[14]李启东.叶片大规模点云处理与无干涉检测规划[D].武汉：华中科技大学，2014.

[15]王立成.复杂曲面原位检测方法与实验研究[D].武汉：华中科技大学，2012.

[16]Sosulin Y G，Kostrov V V.Estimation-correlation-compen sation signal processing in the presence of interferences：A review[J].Journal of Communications Technology and Elec tronics，2006，51（9）：967-1004.

[17]Kim D H，Song J Y.Development of thermal deformation compensation device and CNC based real-time compensation for advanced manufacturing[J].International Journal of Auto motive Technology，2013，14（3）：423-428.

The Research on On-site Inspection and Compensation Machining Method for Aviation Thin-walled Parts

WANG Gang，TONG Gang，MAO Jin-cheng，LI Wen-long
（School of Mechanical Science and Engineering，Huazhong University of Science and Technology，Wuhan Hubei 430074，China）

Thin-wall parts，such as aviation structures and blades，are key parts of aviation manufacturing，with weak rigidity，difficult machining，complex shape and other technical features.The machining accuracy is very difficult to control for thin-wall parts.This article researched on the on-site inspection and compensation machining method for aviation thin-walled parts，and purposed a mean error compensation method of rule characteristics of thin-walled.Based on this method，segmented compensation method for fine machining of free-form surface characteristics of thin-walled is furtherly purposed.Finally，the experiment of on-site inspection and compensation machining of an aviation blade is executed.After compensation machining，the machining error burst is reduce from 0.15 mm～0.35 mm to-0.04 mm～0.06 mm.The experiment verified that segmented compensation method is effective to reduce the machining error of thin-wall parts.

aviation；thin-walled parts；in machine measurement；compensation machining

V261

A

1672-545X（2017）10-0056-08

2017-07-06

国家自然科学基金资助项目（91648111，51635007）；国家973研究计划（2015CB057304）；武汉市应用基础研究计划（2017010201010139）

王 刚（1992-），男，山东聊城人，博士研究生，主要研究方向为曲面原位检测与补偿加工；童 刚（1990-），男，湖北黄冈人，工学硕士，主要研究方向为原位检测路径规划与误差补偿方法；毛金城（1982-），男，湖北荆门人，工学博士，博士后，主要研究方向为工业检测与机器人操作；李文龙（1980-），男，山东青岛人，工学博士，副教授，主要研究方向为航空叶片检测、机器人操作。