基于稳定性图表法和数值模拟的采场跨度优化研究

2017-12-28马俊生任高峰张聪瑞褚衍玉彭家斌

中国矿山工程 2017年6期

关键词：矿房采场跨度

马俊生，任高峰，张聪瑞，褚衍玉，彭家斌

(1.中国恩菲工程技术有限公司，北京 100038； 2.武汉理工大学资源与环境工程学院，湖北武汉 430070； 3.大冶有色金属集团控股有限公司，湖北黄石 435100)

基于稳定性图表法和数值模拟的采场跨度优化研究

马俊生1，任高峰2，张聪瑞2，褚衍玉2，彭家斌3

(1.中国恩菲工程技术有限公司，北京 100038； 2.武汉理工大学资源与环境工程学院，湖北武汉 430070； 3.大冶有色金属集团控股有限公司，湖北黄石 435100)

合理的采场结构参数是地下矿山安全生产、取得良好经济效益的关键问题之一。针对新疆萨热克铜矿所采用的分段空场嗣后充填采矿法，结合现有开拓、采准工程，利用工程岩体分级结果，采用Mathews稳定性图表法分析采场跨度，并结合数值模拟方法，对典型采场跨度尺寸进行数值计算，从位移和应力变化规律两个角度进行分析，得到了采场跨度的合理值为12m。

空场采矿法；岩体分级；采场跨度；稳定性图表法；数值模拟

1 前言

近年来，空场嗣后充填采矿法因其适用范围广、损失贫化较小、作业环境较为安全、回采强度大等诸多优势，在国内外多座矿山得以广泛运用[1～2]。对于空场嗣后充填采矿法而言，采场跨度越大、间柱尺寸越小，开采损失就越小，生产效率就越高，但是过大的采场结构参数往往使得顶板暴露面积增加，容易引起矿岩整体失稳、顶板突发性冒落、冲击地压等矿山安全事故。结合矿山现有开采技术条件，研究合理的采场结构参数是控制顶板暴露面积，减少地压灾害、实现矿体安全高效开采的重要措施。

根据影响岩体稳定性的各种因素，将工程岩体分成若干稳定性不同的级别的过程称为工程岩体分级。目前，国际和国内广泛应用的分级方法主要有：美国人迪尔[3]提出的RQD分级方法、 Bieniawski[4]等人于1974年提出的RMR分类法、Barton[5]于1974年提出的Q分类法以及1995年我国颁布实施的《工程岩体分级标准》[6]。

针对采场结构稳定性研究，国内外专家学者提出了诸多理论研究和实践方法。经验类比法参照类似工程对采场结构参数进行设计，往往缺乏定量数据支撑，主观性较大。理论分析法需要对采场和围岩进行受力分析，采用弹性模型和弹塑性理论进行求解并判断采场的稳定性[7～9]，运用理论分析方法需要假设岩石为各向同性的连续介质，同时还需要对矿体的形态进行简化，其分析结果往往不准确，适用范围有限。数值模拟法多以弹塑性力学为基础，利用数值模拟软件建立的三维结构模型，分析不同结构参数条件下的位移、应力结果来确定最优采场结构参数[10]。叶加冕[11]等对塘子凹矿山采场的3种结构参数进行了模拟计算，通过不同模拟方案的应力和位移变化规律，得到采场的最佳结构参数。李学锋[12]等针对深部开采的特殊环境条件，采用非线性三维有限元程序，结合动、静态数值模拟试验进行采场结构参数优化，确定机械化盘区上向高分层充填采矿法的合理参数为采场宽度8m，分层高度4m。顾晓春[13]结合工程地质调查和岩体质量分级结果，利用FLAC3D软件对采场结构参数优化，确定盘区长为50m、宽为36m，间柱宽为5m时是最合理的采场结构参数，随后进行了工业试验，其结果也验证了优化结果。

总结国内外专家学者所开展的工作，各种分级方法均有侧重，目前在岩体分级的实践中，通常采取结合多种分级方法并相互验证的做法。在采场跨度优化研究方面，数值模拟以其较低的成本和较高的精度仍是目前最为常见的分析方法。

本文以新疆萨热克铜矿为研究对象，结合工程地质调查及工程岩体分级，采用Mathews稳定性图表法和数值模拟分析方法，分别从半定性半定量研究和定量研究两个方面，分析不同采场跨度参数条件下矿体和围岩的稳定性情况，以期获得最优采场跨度参数。

2 工程概况

萨热克铜矿为沉积—改造型砂砾岩铜矿,位于新疆克孜勒苏柯尔克孜自治州乌恰县乌鲁克恰提乡境内，大地构造位置为塔里木盆地西南中新生代坳陷西北缘的次级盆地—托云盆地。矿区构造简单，总体构造线方向为北东向。萨热克铜矿共有Ⅰ、Ⅱ- 1、Ⅲ号矿体，其中Ⅰ号矿体长1 000m、平均铅垂厚度10.43m，产于灰、浅灰绿色砾岩中。矿体呈层状，产状170°～ 160°∠65°～56°，与地层一致。矿体上、下盘围岩均为砾岩、砂岩、粉砂岩，细粒—中粒致密块状，特别是近矿部位硅化强烈，岩石坚硬，稳固性好。矿体内及后期断裂不太发育，多呈平行的小断面，贯通性差；矿石为沉积加改造型，较坚硬。

萨热克铜矿Ⅰ号矿体主要采用空场嗣后充填采矿法进行开采，采场垂直走向布置，矿房和矿柱宽都是15m，长度即为矿体的水平厚度，中段高60m，分为4个分段，每分段高15m。回采分为两个步骤，回采顺序是先采矿房，后采矿柱，矿房隔一采一。采用中深孔凿岩台车在分段凿岩巷道内凿上向扇形炮孔，采用装药器装药，非电导爆系统起爆。爆下的矿石采用柴油铲运机出矿，待矿房矿石全部出完后，集中一次充填，充填采用全尾砂胶结充填。

3 基于工程岩体分级的采场参数设计

3.1 工程岩体分级

利用RQD法、Q体系法、RMR法，结合工程地质调查结果，对萨热克铜矿围岩、矿体质量进行分级。统计矿体钻孔和围岩钻孔RQD数据如表1所示。

表1 矿体钻孔RQD统计

矿体点荷载强度(PLS)、单轴抗压强度(USC)及节理裂隙分布情况由现场试验调查获得，汇总Q体系及RMR体系评价结果如表2所示。

根据表2统计的结果，矿体位置由Q法评分结果为8.22分，属于“一般”类岩体。RMR分级方法计算结果为68分，属于Ⅱ级“好岩体”。

表2 岩体分级结果

Q值与RMR值可以通过巴顿提出的转换公式进行转换，如下：

RMR=9ln(Q)+44

(1)

转换后所得的逆向RMR评价值为62.96，与RMR分级正向评价结果68非常接近；同样，围岩质量评价中，根据Q法评分数值为16.68，属于“好”类岩体，经由公式转后计算RMR值为69.33，与正向RMR评分74也十分接近。

由此也可说明两种岩体质量评价标准都可以完成针对萨热克铜矿岩体质量的分级，同时结果均能有效反映岩体的稳定性。

3.2 基于Mathews图表法的采场跨度设计

3.2.1 稳定性图表理论

Mathews稳定性图表法最早由Mathews等人于1980年提出，而后经由Potvin[14]更新数据进行了改进。运用Mathews法进行稳定性分析首先需要确定两个参数：稳定性系数N和采场形状系数S，其计算方法见式(2)：

(2)

式中：A——岩石应力系数；

B——节理方位修正系数；

C——重力调整系数；

L——暴露面的长度；

H——暴露面的宽度；

Jr——节理粗糙系数；

Jn——节理组数；

Ja——节理蚀变系数。

图1是一个典型的稳定性图表，从上至下的两条曲线，将坐标区域划分为稳定、不稳定和塌落3个区域。根据目前的采场结构参数可以推断采场的稳定性，也可以通过确定稳定性系数反算采场的极限暴露面积和采场尺寸。

图1 稳定性图表(1989年)

根据岩体分级指标和采场顶板尺寸参数，可以计算得出修正Q指标评级及采场形状系数S，如式所示：

(3)

3.2.2 稳定性系数计算

为了确定采场的稳定性系数，需要确定岩石应力系数A、节理方位修正系数B、以及重力调整系数C。确定岩石应力系数，首先应当确定暴露表面中间平面的诱导应力大小，而诱导应力通常难于测量，因此需要根据原岩应力值进行推算[15]。本次试验选取的2 730m中段106#采场，距地表170m，根据式(4)可以计算出垂直应力：

(4)

式中：σv——垂直应力；

γ——岩石容重；

σh——水平应力；

K——侧压系数。

侧压系数由式计算，并计算水平应力：

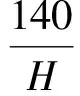
(5)

通过计算，所得结果如式(6)所示：

(6)

考虑采场顶板作为主要暴露面，在采场顶板中间平面上σv=4.59MPa、σh=7.34MPa、K=1.6 ，高跨比M=80/15=5.3 。根据图2所示的诱导应力推断曲线可以得出σ1/σv=4.3 ，因此诱导应力σ1=4.3×σv=19.737MPa。则单轴抗压强度与诱导应力比值σc/σ1=93.12/19.737=4.72。

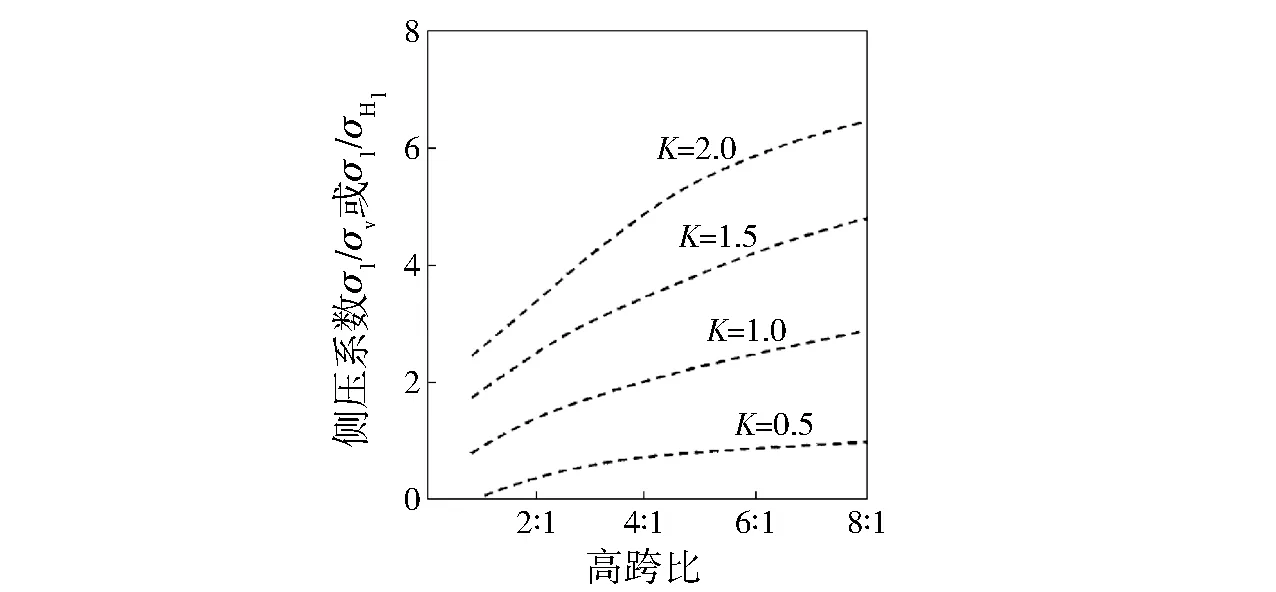
图2 诱导应力推断曲线

应力系数A的取值与σc/σ1的大小成线性关系，如式所示，因此，顶板岩石应力系数A=0.406：

(7)

B值大小需考虑不连续面的方向，需根据优势节理方位与采场表面方向之间的夹角来确定和计算。将采场顶板近似考虑成一水平面，根据优势节理组调查统计结果，两条优势节理组分别为160°∠41°、331°∠49°，根据取值函数，考虑节理方位修正系数，取B=0.5。

重力调整系数C是考虑重力作用对顶板的影响远大于对侧帮稳定性的影响所设计的修正系数，其值的大小按照公式(8)计算：

C=8-6cosα

(8)

式中α为暴露面与水平面的夹角，确定重力调整系数C=2。

根据以上讨论，可以得出稳定性系数N=Q′×A×B×C=12.65，形状系数S=6.32，结合图1可以看出，此时采场稳定性位于过渡区中，存在破坏的可能，这一情况也与现场工程实际吻合。

基于上述分析，根据目前的稳定性系数，当采场形状系数取S=5 时，采场位于稳定区和过渡区边界上，因此，取形状系数S=5为采场极限形状系数。根据形状系数的定义和现场实际进路长80m的现状，反算出采场跨度约为12m。

4 FLAC3D数值模拟

4.1 模型建立

模型长度和跨度均为400m，高度为500m，采场跨度大小分别设计为10、11、12、13、14、15m，高度取矿房高度，为15m，采场长度为80m。

选用《工程岩体分级标准》作为岩体力学参数选择的依据，因此需要获取岩体的完整性系数Kv，完整性系数Kv与岩体体积节理数Jv存在对照关系，且体积节理数Jv可由现场RQD结果由公式(9)计算得到[16]：

RQD=110-2.5Jv

(9)

总结修正后的围岩基本质量指标如表3所示。

表3 修正的围岩基本质量指标[BQ]值

根据表3中的岩体基本质量指标修正值[BQ]，岩体物理力学参数的计算采用文献[17]中的拟合公式，如式(12)所示：

(10)

得到计算所采用的岩体参数见表4所示。

采用位移边界条件，即模型的X方向、Y方向和底部边界均施加位移约束条件，上边界为自由边界。本构模型选用摩尔—库伦准则，采用八节点六面体实体单元Solid45进行模拟。由于矿体埋深较浅，围岩初始应力场仅考虑自重应力。

4.2 采场稳定性分析

对设计的6种采场跨度方案进行了计算分析，采场的主要变形集中在采场的顶板与底板，其变形值分布在10～15mm之间。为了研究不同采场跨度下巷道位移变形规律，在巷道内每隔4m设置监测点，测量其位移值，变化趋势如图3所示。

表4 岩体物理力学参数

从图3可以看出：①矿房开采将导致顶板发生沉降而底板产生隆起，随着采场跨度的增加顶板的沉降和底板的隆起均有增加，顶板的沉降从9.89mm增加至14.52mm，而底板的隆起从9.41mm增加至14.23mm；②顶板位移分布呈现出中间沉降大、两边沉降小的规律，最大沉降大致位于巷道最中部；③底板隆起的位移规律与顶板不同，远离阶段运输巷道的一端隆起较小，随着掌子面开采到一定的范围后，底板隆起值变化不大，达到稳定的状态。

图3 顶板和底板位移变化规律

为了判断采场跨度的极限值，提取了各计算工况下顶板与底板的最大变形值，如表5和图4所示。

对顶板和底板最大变形值进行统计和分析后可以发现，采场跨度由10m增加到15m时，采场顶板与底板的变形随跨度增加而递增；顶板位移值在当矿房跨度达到12～13m时出现一个稳定期，随后顶板位移急剧增大；同样，底板位移在矿房跨度在11～12m时出现一个缓慢增加的区域。综合分析认为采场跨度达到12m左右后，围岩进入了塑性状态，局部产生了岩体屈服，即进入不稳定状态。因此就采场的局部稳定性而言，12～13m是采场稳定的极限跨度区间。

表5 不同采场跨度顶底板位移变化

针对单采场开采时的应力变化情况，巷道断面应力云图如图5所示。为了研究不同采场跨度下巷道应力变化规律，在巷道内每隔4m设置监测点，测量其应力，并获取巷道内最大主应力、最小主应力及最大剪应力大小，如表6所示，绘制应力随采场跨度变化曲线如图6所示。

结合应力等值线图和变化趋势图可以看出：①单采场条件下，矿房最大主应力一般发生在矿房4个边角处，这是由于矿房四角属于尖锐位置，极易产生应力集中；②最大主应力、最小主应力和最大剪应力大小都随着矿房跨度的增大而产生变化。其中，最大主应力和最大剪应力的值在跨度为12m时达到最小，随后急剧变大；而最小主应力的值也在跨度为11～13m范围内变化较小，一旦跨度超过13m，最小主应力的大小也产生剧烈的变化。因此，从应力变化的角度分析，矿房极限跨度值应在12m左右为宜。

4.3 隔一采一条件下稳定性分析

单采场模型的分析始终无法全面地反应矿山开采所带来的位移、应力变化规律，所得的极限跨度是在最为理想的情况下得出的，因此还需要利用单采场的分析模型，对隔一采一工艺条件下采场的矿岩稳定性进行数值模拟研究，验证极限跨度的合理性。

分别对6种不同采场跨度尺寸进行建模和模拟，可以看出隔一采一情况下采场的主要变形仍然集中在采场的顶板与底板，其变形值大致在11～16mm之间，统计不同采场跨度下顶板、底板变形最大值，绘制变形随跨度变化曲线如图7所示。

图4 顶板和底板位移随采场跨度变化规律

图5 巷道断面应力云图

表6 不同采场跨度围岩应力变化

图6 围岩应力随采场跨度变化规律

从表7和图7可以看出，隔一采一工况下，围岩的变形规律与单采场的计算结果基本一致，即采场跨度由10m增加到15m时，采场顶板与底板的变形逐渐增加，当采场跨度超过12～13m后，采场变形值呈非线性增加。因此在隔一采一情况下，12～13m是采场稳定的极限跨度区间。计算结果表明，采场自身稳定性基本不受周边采场的开采活动影响。

图7 隔一采一位移随采场跨度变化规律

表7 不同采场跨度位移最大值

为了分析隔一采一条件下矿房应力变化情况，获取典型断面应力云图，如图8，并获取巷道内最大应力值大小如表8所示，绘制应力随采场跨度变化曲线，研究应力随跨度变化规律，如图9。

图8 隔一采一巷道断面应力云图

表8 不同采场跨度围岩最大应力值

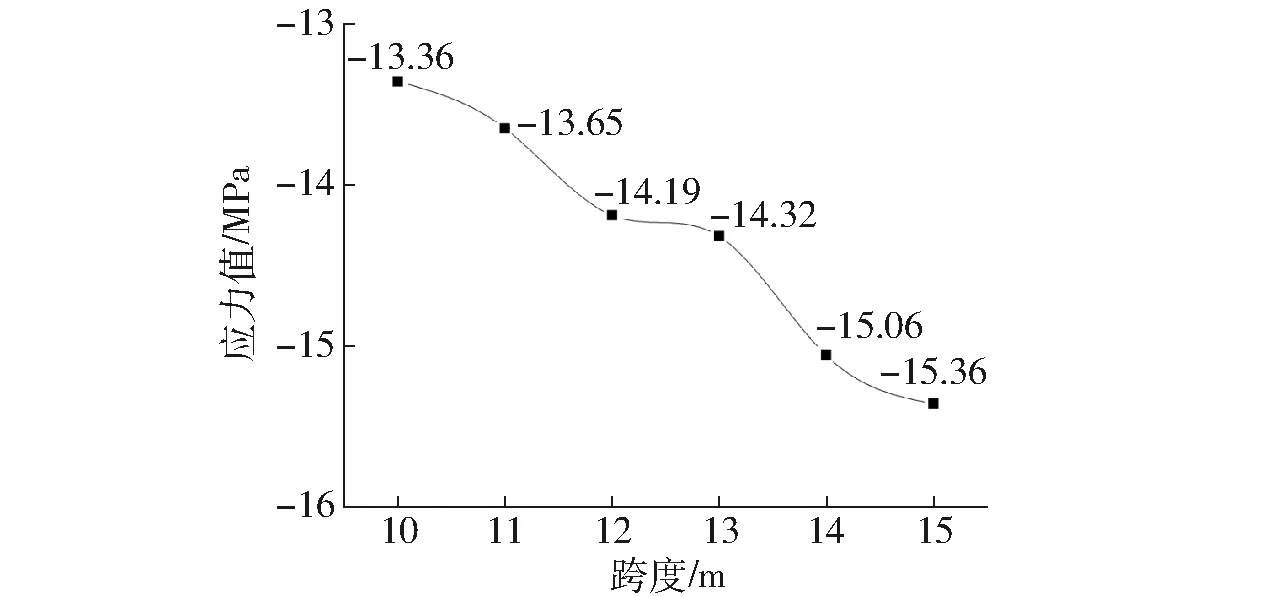
图9 隔一采一围岩应力随进路跨度变化规律

从计算结果可看出：①隔一采一情况下采场进路应力集中的区域产生了变化，除了在矿房四角产生集中外，在相邻矿房中部产生了集中，其应力变化大致在13～16MPa之间；②隔一采一工况下，围岩的应力变化规律与单采场的计算结果基本一致，即采场跨度由10m增加到15m时，采场应力大小逐渐增加，当采场跨度超过12～13m后，采场应力值呈忽然增大。因此在隔一采一情况下，12～13m是采场稳定的极限跨度区间。

5 结论

通过对单采场条件和隔一采一工况下不同采场跨度时的位移、应力变化情况进行分析，得到以下结论。

(1)可综合利用岩体质量评价中的Q系统和RMR分级法对采场围岩和矿体进行分级，确定了萨热克铜矿围岩和矿体的稳定性均为Ⅱ级。

(2)基于工程岩体分级结果，采用修正的Mathews稳定性图法对采场跨度进行计算，结果表明，目前采场所采用的15m跨度方案存在潜在坍塌的危险，推荐采场跨度减小为12m。

(3)利用数值模拟方法，从定量研究的角度，确定空场嗣后充填采矿法的合理跨度为12～13m，与利用稳定性图法所得跨度值吻合，建议矿山在后续采准工程中减小跨度以保障矿山安全。

(4)矿房形成空场后，位移变化主要集中于顶板和底板，又以顶板沉降值最为明显，并且，顶板沉降的最大值一般在空区的中部，应当注意此处顶板冒落现象，加以防范。

(5)应力场分布结果表明，隔一采一条件下的应力集中位于矿房的四角处，并对中间采场有一定影响，后续开采中间采场时，需保证充填质量。

[1] 谢永生.分段空场嗣后充填采矿法在巴基斯坦杜达铅锌矿的研究与应用[J].有色金属工程,2012，(1):39-43.

[2] 任红岗,谭卓英,蔡学峰,等.分段空场嗣后充填法采场结构参数AHP-Fuzzy优化[J].北京科技大学学报,2010，(11):1383-1387.

[3] Deere.Technical description of rock cores for engineering purposes[J].Rock Mech Rock Eng,1964,(1):17-22.

[4] Bieniawski Z T.Engineering classification of jointed rock masses[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1974,(12):244.

[5] Barton N,Lien R,Lunde J.Engineering classification of rock masses for the design of tunnel support[J].Rock mechanics,1974,(4):189-236.

[6] GB50218-94，程岩体分级标准[S].1995.

[7] 薛琳.直墙拱形隧道围岩粘弹性位移解析解[J].岩土工程学报,1996，(6):100-105.

[8] 喻勇,张宗贤,俞洁,等.岩石直接拉伸破坏中的能量耗散及损伤特征[J].岩石力学与工程学报,1998，(4):38-44.

[9] 刘保国,杜学东.圆形洞室围岩与结构相互作用的粘弹性解析[J].岩石力学与工程学报,2004，(4):561-564.

[10] Li S,Pan H,Kong T,et al.Numerical simulation and analysis of underground pressure in the 101 fully-mechanized top coal caving face of the Tingnan Coalmine[J].Journal of Coal Science and Engineering (China),2009,15(1):28-32.

[11] 叶加冕,蒋京名,王李管,等.采场结构参数优化的数值模拟研究[J].中国矿业,2010，(3):61-65.

[12] 李学锋,谢长江.深部高应力区采场结构参数优化研究[J].矿冶工程,2004，(6):11-13.

[13] 顾晓春.高山复杂矿体采场结构参数优化研究[J].采矿技术,2009，(1):1-3.

[14] Potvin Y.Empirical open stope design in Canada[D].The University of British Columbia (Canada), 1989.

[15] Mawdesley C,Trueman R,Whiten W J.Extending the Mathews stability graph for open-stope design[J].Mining Technology,2001,(1):27-39.

[16] Palmstrom A.Measurements of and correlations between block size and rock quality designation (RQD)[J].Tunnelling and Underground Space Technology,2005,20(4):362-377.

[17] 景锋，边智华，陈昊，等.不同岩性侧压系数分布规律的统计分析[J].长江科学院院报，2008，(4):48-52.

Research on the optimization of stope span based on stability chart method and numerical simulation

Reasonable stope structure parameters in underground mine is one of the key issues of safety production and good economic returns. Combined with the existing development，mining preparation engineering，results of rock mass classification and based on the subsequent backfilling mining method of Sarke Copper Mine, Mathews stability chart method was used to analyze the limit span of stope. At the same time, based on numerical simulation of the typical span size of the stope from the aspects of displacement and stress change law, the conclusion was obtained that the reasonable value of the stope span was 12m.

open-stoping method; rock mass classification; stope span; stability chart method; numerical simulation

TD853.32