四点长基线深海定位模型建立方法及精度分析

林冠英, 刘 蔚, 周保成, 许铭彬



四点长基线深海定位模型建立方法及精度分析

林冠英, 刘 蔚, 周保成, 许铭彬

(国家海洋局南海调查技术中心, 广东 广州 510300)

高精度水下定位技术对于维护国家海疆安全、海洋权益和国民经济建设具有十分重要意义和实际应用价值。根据射线在水中的传播特性, 利用双曲面定位方法建立长基线深海定位模型, 通过计算机仿真获得4 000 m水下信源在10 km2正方形范围内的定位误差精度及分布规律。结果表明: 浮标网络中心位置定位精度最高, 可得到亚米级; 离中心位置越远, 定位精度越差。

长基线; 深海定位; 双曲面模型; 定位精度

众所周知, 陆地上的精准定位, 可以通过全球定位系统(GPS)实现。但是卫星信号在水中不能传播, 因此GPS无法实现水下定位。人们通过研究发现, 声波可以在水中传播, 特别是低频声波可以传播上百公里。因此, 可以模仿GPS在空气中传播的结构, 在水面布放能精准定位的智能浮标作为基点, 类似空中GPS卫星的功能, 通过其搭载的声学通信机与水下设备通信, 从而将陆地上的GPS延伸至水下, 达到水上水下公用一个定位坐标系的效果。这就是水下长基线定位的基本原理。

国外在水下定位技术方面的研究起步较早, 目前在这方面应用较为成熟的国家是英国和法国。最为典型的是法国IXBLUE公司生产的POSIDONIA6000定位系统, 该系统是基于超短基线的方法, 最深可以定位6 000 m。而国内方面, 中国科学研究院声学研究所、哈尔滨工程技术大学、国家海洋局海洋技术研究所等单位在水下定位技术方面都进行过多种理论研究[1-2]。但国内的研究水平与国外还是有很大的差距, 定位误差较大, 而且大部分还停留在浅水研究试验阶段, 在深海资源探测等定位应用中, 目前仍然依靠购买国外的设备。

21世纪是海洋的世纪, 随着人类社会和技术的向前发展, 人们的生产活动从陆地延伸到了海洋。特别是石油开采、海底资源开发等都需要对水下设备进行精准定位, 因此研制精准的水下定位系统成为推进海洋工程发展的重要手段[3]。但受到技术、资金等方面的局限, 深海精准定位难度较大, 目前较为常用的方法是长基线定位方法。为了研究基于长基线的深海定位系统性能, 本文将海水介质分成许多水平的均匀薄层, 在每层中可以近似认为声速对于深度是线性变化关系, 根据射线在水中的传播理论提出了一种基于智能浮标的长基线定位系统模型。进一步通过计算机仿真的方法建立该模型, 并对模型中4 000 m水深位置的定位性能进行了分析讨论。

1 水下定位原理及观测设备的布放

水下声学定位技术是在声呐技术之后才开始出现, 其原理是通过声波在信标与目标之间的传播时间、相位变化等计算出距离, 再根据定位模型算出三维坐标, 从而实现定位。按照基线的长短, 通常把水下定位系统分为3类[4]: 超短基线定位系统(USBL)、短基线定位系统(SBL)和长基线定位系统(LBL), 具体参数如表1所示。

USBL一般是用3~4个相距几厘米且相互垂直的接收单元组成接收阵列, 通过计算信号到达各接收单元之间的相位差以及信号源与接收阵列的斜距, 从而对水下信号源进行定位, 该方法主要用于短程定位, 长距离定位时误差较大[5]。SBL一般是在船底相距几十米的位置安装几个水听器, 水听器之间的距离和夹角已知, 通过测量水下信号源信号到达各水听器之间的时间差和相位差, 计算出水下信号源的坐标, 该方法主要用来定位中等距离的目标, 目前比较少用。LBL是在海底已知位置布放3个以上的定位信标, 利用声学换能器进行通信, 通过计算水下定位目标与信标之间的距离进行定位[6], 用于长距离的定位, 定位精度比其他两种方式的都高, 但需要事先在海底布放已知位置的信标。本文主要针对深海定位系统模型进行研究, 因此选用长基线的定位方法。传统长基线定位方法需要在海底布设信标, 而且需要对信标位置进行校准, 实现起来较为复杂。因此本文采用水面GPS智能浮标代替水下固定信标, 定位原理相同, 但与传统长基线定位系统相比操作便捷, 可快速安装, 无须对信标进行校准, 如图1所示。

表1 传统水声定位系统分类表

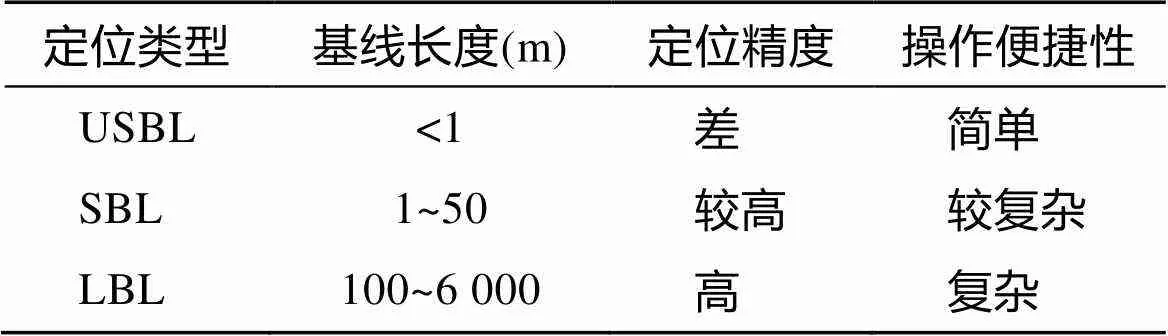
Tab.1 Classification of a traditional acoustic positioning system

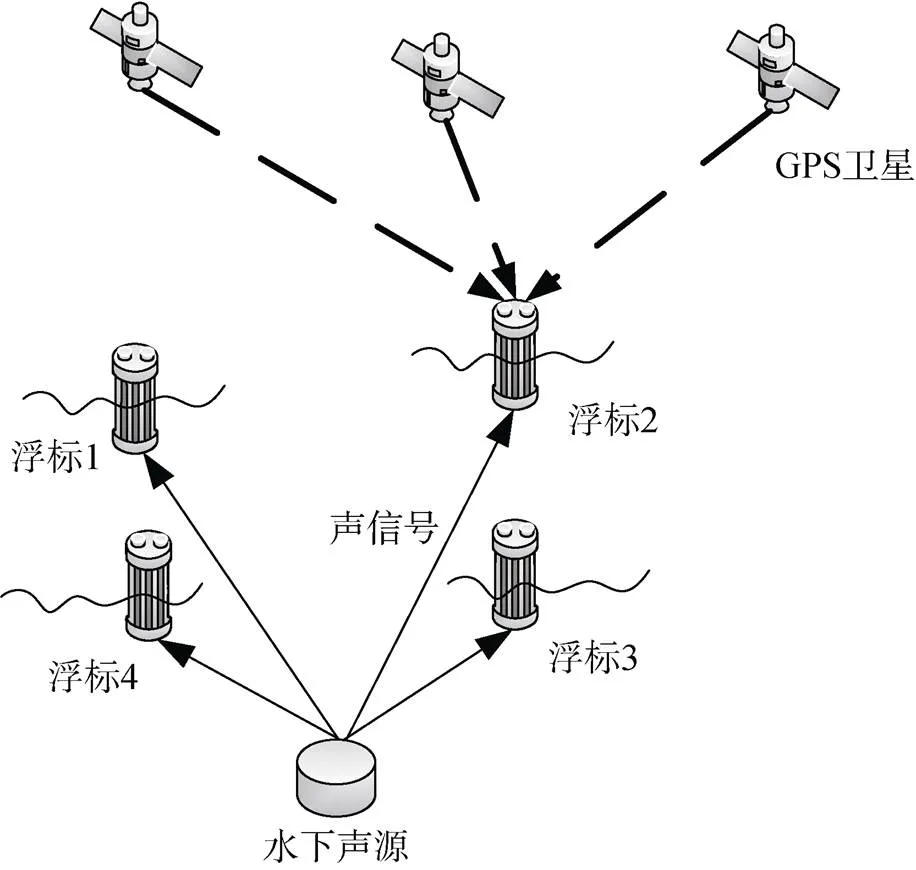
图1 深海长基线定位系统示意图

水下GPS主要有两种定位模型: 球面模型和双曲面模型。球面模型是通过测量水下目标与多个水面浮标之间的距离, 通过空间交汇的方法, 计算出水下目标的坐标[7]。该模式需要测量水下信号的发射时刻, 所有水下目标的时钟需要与浮标系统的时钟同步, 时钟同步的误差将直接影响测量精度, 同时增加系统的复杂度。而双曲面模型相比于球面模型, 最大的优点是通过差分的方式消除了时间变量, 从而避免了同性误差对定位精度的影响, 因此不需要在水下目标中安装精准的原子钟, 只需要利用GPS授时的原理, 对各浮标进行系统同步即可。因此本文采用双曲面模型作为长基线深海定位模型进行仿真与分析, 该模型表达式为:

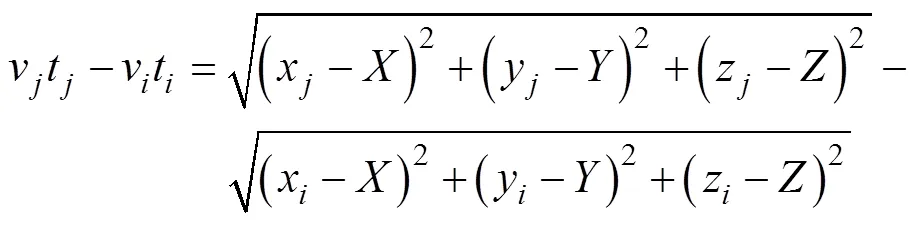
式中,、分别表示水下信源信号到达第号和第号水面接收器(GPS浮标)所经路径上的平均声速,、为信号经相应路径到达接收器的时间, (,,i)、(,,) 为号和号水面GPS浮标的坐标, ()是水下信号源的坐标。该式子中含有三个未知量, 因此需要至少4个浮标组成的方程组才能计算出水下目标坐标。

2 四点长基线模型建立方法

根据观测方程, 可以通过建立数学模型, 求算射线在水中的传输路径。

2.1 已知条件与未知量求解方法

在双曲面定位模型中, 水面浮标的位置是实时可测的。在智能浮标中安装GPS接收机, 其工作在RTK(real-time kinematic, 载波相位差分技术)模式, 定位精度在厘米级[8]。当要求水下目标的定位精度在米级水平时, 采用 RTK模式, 浮标的虚拟基线的误差可以认为忽略不计。

由式(1)可知, 需要解算水下信源的坐标, 还需要知道该海域的水声传播速度和声线在水中的传播时间。射线在水中的传播遵循斯涅尔定律, 因此射线路径跟声速相关。信号发射角为垂直水平面的法线与射线的夹角, 用表示。将海水假设成由很多薄薄的平行层组成, 每层为均匀层, 并且射线在传播过程中层与层之间只有折射没有反射。用12, …,1…来表示各层, 设第和1层的声速为c和c1, 则在它们的分界面上有[9]:

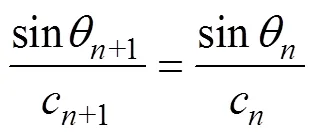
将海水分成个等声速层, 每层厚度为, 各层内以固定声速传播, 即有射线经过的水平距离、实际路径长、传播总时间分别为:

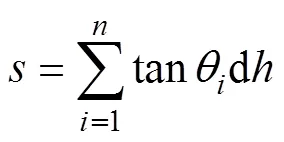
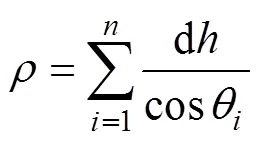
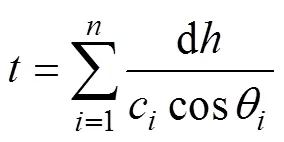
式中, 第层的声速表示为c, 其信号发射角表示为θ。因此, 只要知道声速资料, 就可以通过射线追踪的方式, 模拟出该海域的定位数据。

2.2 声速剖面计算

海水的声速是温度、盐度、压力的函数, 通常以经验公式表示[10]。海水声速可以通过声速剖面仪直接测量, 也可以根据全球Argo计划提供的温盐剖面资料[11], 按照声速计算的经典公式求得, 比较常见的公式有: Wilson, Leroy, Chen And Millero, Del Grosso, Mackenzie, Medwin等。图2是根据中国南海某海域实测温盐深资料利用Mackenzie公式计算出的声速剖面图。其中超过1 500 m深度的声速数据是根据声速随深度变化的理论公式计算得到的, 该剖面符合深海典型声速剖面形式。

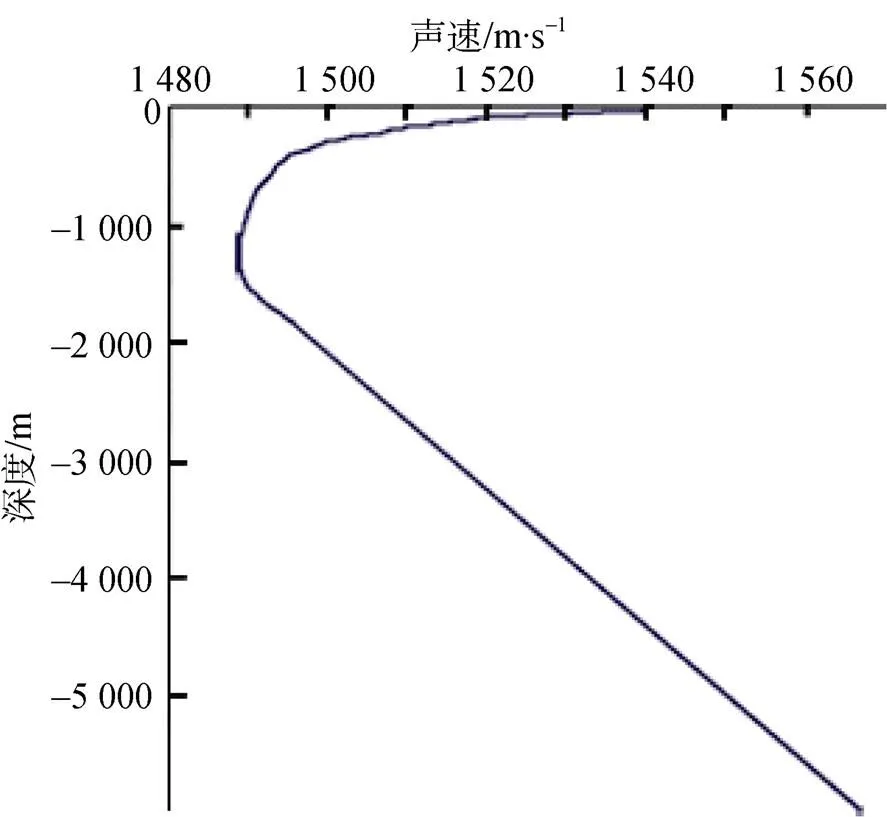
图2 深海声速剖面图

2.3 建模步骤

把海水假设成由很多均匀的薄层组成, 因此射线在水中的传播符合斯涅尔定律。将水面上的任意一点设为原点, 以垂直水面向上的方向为轴,轴与轴相互垂直, 且处于水平面上。轴、轴与轴符合右手定则。那么, 水深已知, 便可以通过射线追踪的方式模拟出该水深的定位观测数据, 步骤如图3, 具体如下:

(1) 利用声速剖面仪, 测量出该区域的声速剖面资料; 或者通过查海水的温盐深资料, 通过经典公式计算出声速剖面数据。

(2) 设定浮标坐标 () 、水下信号源初始坐标()。

(4) 设信号源的初始发射角为, 按公式(3)计算信号射出水面时的坐标点与信号源之间的水平距离′。

(5) 比较两距离差, 给定一阈值>0。若<, 转到第7步; 若>, 转到第6步。

(6) 若>, 则减小发射角度; 若<–, 则增大发射角度。重新设置初始发射角后, 转到第4步继续运行。

(7) 退出循环, 得此时信号初始发射角为, 由此发射角根据公式(4)、(5)便可以求出声线路径和信号传播时间。计算声线平均声速:。

(8) 给定多个浮标 (, y , z) (1, 2, …,), 根据以上步骤继续分别求出它们的线传播时间及平均声速, 便可以模拟出该定位系统的所有观测数据。

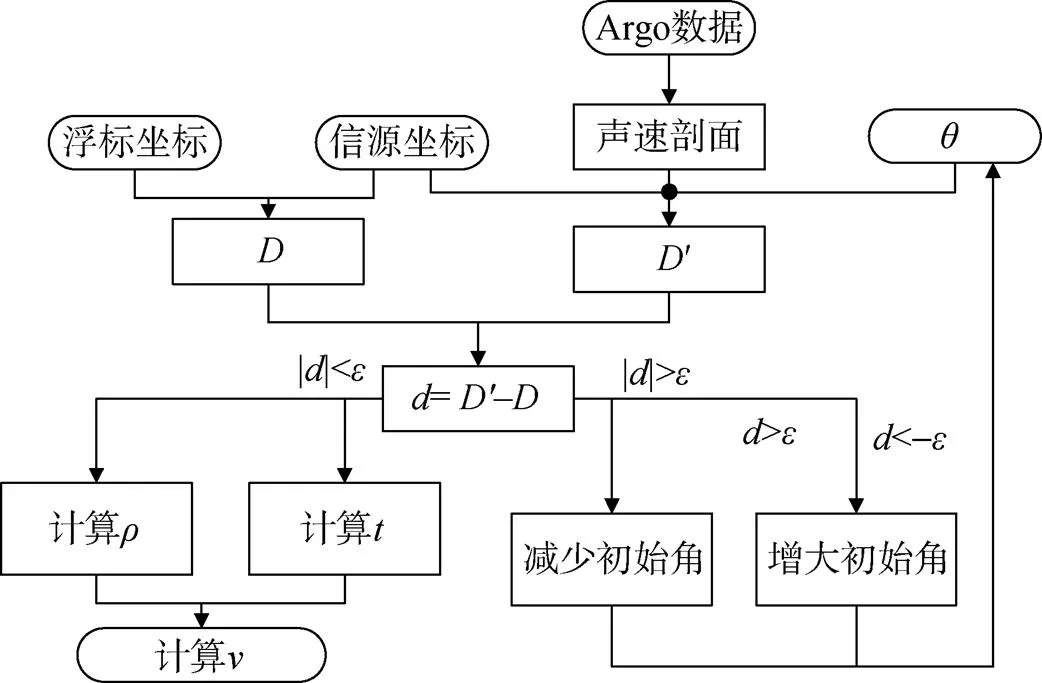
图3 建模流程图

3 定位精度分析

射线弯曲, 使得射线实际传输路径各异, 不同路径的声速也不一样。而实际上声速剖面的测量误差将对定位精度产生较大影响, 因此本文不使用统一的声速值, 而是根据射线追踪理论对不同射线角的路径单独计算平均声速。同一精度水平的水声传播误差, 在不同形状的水下空间网的作用下, 对水下定位误差的影响不同。浮标网形的布设多种多样, 实际应用中也很不规则, 为了研究方便, 常把其规则化。常用的浮标布站方式有菱形、星形(Y形)和倒三角形。薛树强[12]均在研究中对星形网的定位精度作了肯定。在此, 也选用星形网进行相关分析。

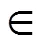
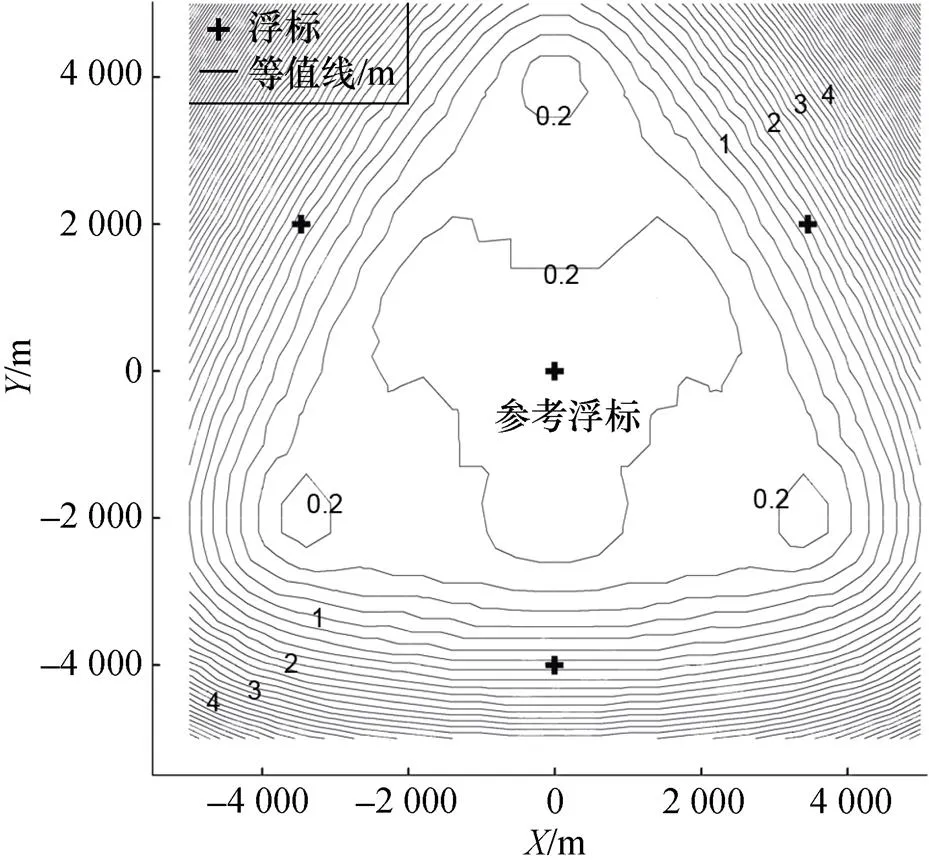
图4 水平定位误差等值线图

根据结果分析如下:

(1) 精度程度

该浮标布设模式下, 目标离中间浮标距离越近定位精度越高, 随着距离的增大其定位精度逐渐下降, 中间一枚浮标正下方的点位精度最高, 水平定位几乎无误差, 垂直定位精度可达0.2 m。浮标网形所构成的倒三角范围内水平定位误差优于1 m。网形外围区域随着距离的加大精度越来越差, 但大部分区域水平定位精度优于4 m; 垂直定位精度优于10 m, 相对于水深的精度优于2.5×10–3(为水深, 本文中=4 000 m)。

(2) 精度分布

水平定位精度分布: 中间一定区域声线距离差较小, 浮标的影响较大, 精度等值线向外部3枚浮标方向凸起, 随着某个或某些声线方向上的距离差增大, 声线弯曲的影响增大, 离浮标较近处定位精度下降, 而在无浮标方向上由于这种距离差通过差分的形式在一定程度上得以较大削弱, 得到了较高的定位精度, 其定位精度等值线呈以无浮标方向为顶点的三角形。

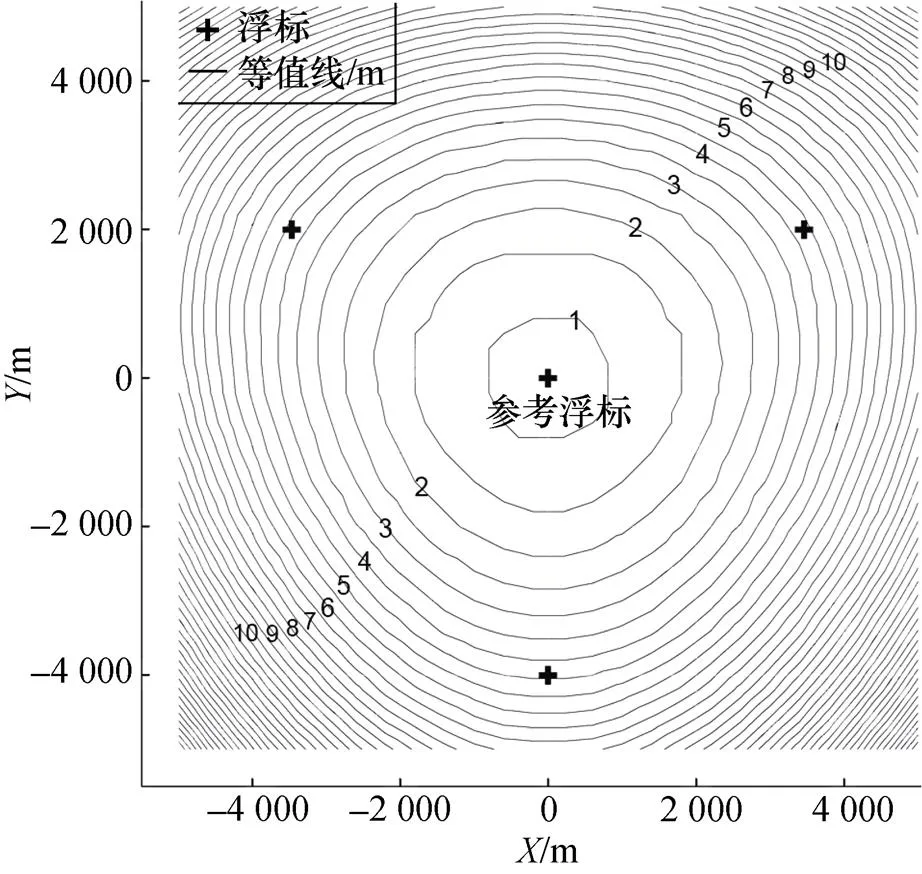
图5 垂直定位误差等值线图

表2 四枚浮标在网形中的坐标

垂直定位精度分布: 垂直定位精度受浮标的影响较大, 离浮标越近定位精度越高, 其精度等值线始终呈现以浮标为顶点的三角形。

4 结论

[1] 王泽民, 罗建国, 陈琴仙, 等. 水下高精度立体定位导航系统[J]. 声学与电子工程, 2005, 2: 1-3. Wang Zemin, Luo Jianguo, Chen Qinxian, et al. Underwater high precision stereo navigation system[J]. Acoustics and Electronic Engineering, 2005, 2: 1-3.

[2] 王权, 程鹏飞, 章传银, 等. 差分GPS水下立体定位系统[J]. 测绘科学, 2006, 31(5): 18-21.Wang Quan, Cheng Pengfei, Zhang Chuanyin, et al. Under water positioning system based on DGPS[J]. Science of Surveying and Mapping, 2006, 31(5): 18-21.

[3] 姜静波, 徐永平, 李思忍, 等. 多参数海洋浮标实时采集系统的设计[J]. 海洋科学, 2014, 38(12): 99-102. Jiang Jingbo, Xu Yongping, Li Siren, et al. Design of multi-parameter ocean buoy data acquisition system[J]. Marine Sciences, 2014, 38(12): 99-102.

[4] 田坦. 水下定位于导航技术[M]．北京: 国防工业出版社, 2007. Tian Tan. Underwater Positioning in Navigation Technology[M]．Beijing: National Defense Industry Press, 2007.

[5] 王燕, 梁国龙. 一种适用于长基线水声定位系统的声线修正方法[J]. 哈尔滨工程大学学报, 2002, 23(5): 32-34.Wang Yan, Liang Guolong. Correction of sound velocity in long baseline acoustic positioning system[J]. Journal of Harbin Engineering University, 2002, 23(5): 32-34.

[6] 孙树民, 李悦. 浅谈水下定位技术的发展[J]. 广东造船, 2006, 4: 19-24. Sun Shumin, Li Yue. On the development of underwater positioning technology[J]. Guangdong Shipbuilding, 2006, 4: 19-24.

[7] 蔡艳辉, 程鹏飞, 李夕银. GPS伪距改正及精密动态单点定位精度分析[J]. 全球定位系统, 2004, 2: 11-15. Cai Yanhui, Cheng Pengfei, Li Xiyin. Pseudo-range correction and kinematic point positioning accuracy[J]. Gnss world of China, 2004, 2: 11-15.

[8] 赫雷桑诺夫布列霍夫斯基. 海洋声学基础[M]. 朱伯贤, 金国亮, 译. 北京: 海洋出版社, 1985. Hesunenov Brehovsky. Ocean Acoustic Foundation[M]. Zhu Boxian, Jin Guoliang. Beijing: Ocean Press, 1985.

[9] 周丰年, 赵建虎, 周才扬. 多波束测深系统最优声速公式的确定[J]. 台湾海峡, 2001, 20(4): 411-419. Zhou Fengnian, Zhao Jianhu, Zhou Caiyang. Determination of classic experiential sound speed for mulae in multibeam echo sounding system[J]. Journal of Oceanography In Taiwan Strait, 2001, 20(4): 411-419.

[10] 王文杰, 刘宇迪, 亓晨, 等. 南海声速跃层分类及其季节变化[J]. 海洋科学, 2014, 38(8): 82-93. Wang Wenjie, Liu Yudi, Qi Chen, et al. Classification and seasonal variability of the sound velocity spring layer in the South China Sea[J]. Marine Sciences, 2014, 38(8): 82-93.

[11] 张志春, 袁东亮, 李博. 基于Argo浮标的西北太平洋环流特征分析[J]. 海洋科学, 2015, 39(7): 93-102.Zhang Zhichun, Yuan Dongliang, LI Bo. Analysis of circulation structure in the Northwest Pacific Ocean based on Argo profiles[J]. Marine Sciences, 2015, 39(7): 93-102.

[12] 薛树强. 矩阵体积及其在网形设计中的应用[D]. 北京: 中国测绘科学研究院, 2007. Xue Shuqiang. Matrix volume and its application in mesh design[D]. Beijing: China Institute of Surveying and Mapping, 2007.

(本文编辑: 刘珊珊)

Observation data simulation and positioning accuracy analysis of a 4-point long-baseline model in deep water

LIN Guan-ying, LIU Wei, ZHOU Bao-cheng, XU Ming-bin

(South China Sea Survey Technology Center State Oceanic Administration, Guangzhou 510300, China)

High-precision underwater positioning is a widely used technology that is of great significance for the maintenance of national maritime security, maritime rights and interests, and national economic construction. According to the propagation characteristics of radiation in water, the long-baseline deep-sea positioning model is established using the hyperboloid positioning method. The accuracy and distribution of the positioning error of the 4 000 m underwater source in the range of 10 km2are obtained via computer simulation. Results show that the positioning accuracy at the center of a buoy network is the highest, and the sub-meter level is obtained. The positioning accuracy decreases with increasing distance from the center position.

long baseline; deep water positioning; hyperboloid model; positioning precision

[Research and Development of International Submarine Regional Resources, No.1511410312035; Marine Science and Technology Director Fund of South China Sea Branch, State Oceanic Administration , No.1525]

Aug. 16, 2016

TB566

A

1000-3096(2017)08-0086-05

10.11759/hykx20160816001

2016-08-16;

2016-12-18

国际海底区域资源研究与开发项目(1511410312035); 国家海洋局南海分局海洋科学技术局长基金(1525)

林冠英 (1986- ), 男, 广东雷州人, 工程师, 硕士, 主要从事海洋调查与监测研究, 电话: 020-84462802, E-mail: linguanying@smst.gz.cn; 刘蔚,通信作者, 男, 工程师, 博士, E-mail: liuwei@smst.gz.cn