3t+1阶幻立方的一种构造方法

侴万禧, 门 博

(1. 安徽理工大学 土木建筑学院, 安徽 淮南 232001;2. 沈阳师范大学 数学与系统科学学院, 沈阳 110034)

理论与应用研究

3t+1阶幻立方的一种构造方法

侴万禧1, 门 博2

(1. 安徽理工大学 土木建筑学院, 安徽 淮南 232001;2. 沈阳师范大学 数学与系统科学学院, 沈阳 110034)

对幻立方给以简单介绍,阐明幻立方的均衡结构特性,由客船沉没的原因指出幻立方的应用价值。给出了幻立方的一种构造方法,阐明了3t+1幻立方的构造思路和基本步骤。介绍了3t+1阶幻立方构造过程,按照这种构造步骤,给出了t=3时的情况下,10阶幻立方的构造全过程及每一个步骤中的相应结果。最后得到10阶幻立方的10个幻方,解决了3t+1幻方的计数问题。

幻方; 幻立方; 计数

0 引 言

13世纪,中国南宋数学家杨辉在世界上首先开展了对幻方的系统研究,欧洲14世纪也开始了这方面的工作。著名数学家费尔玛、欧拉都进行过幻方研究。如今,幻方仍然是组合数学的研究课题之一,经过一代代数学家与数学爱好者的共同努力,幻方与它的变体所蕴含的各种神奇的科学性质正逐步得到揭示[1-3],已在组合分析、实验设计、图论、数论、群、对策论、纺织、工艺美术、程序设计、人工智能等领域得到广泛应用。

幻立方是幻方向三维空间的自然延伸,是由自然数1到n组成边长为n的正方体,将n3个自然数按顺序依次填入n×n×n立方体中,如图1所示。由上向下是从第1层到第n层的n个划分,每一层均是n行×n列的一个正方形,称之为一个直剖面或一个方阵。同理,立方体还有另2个方向的直剖面:从后向前方向的剖面,从左到右方向的剖面。幻立方是一种轴对称和中心对称图形,具有神奇的均衡结构[4-6]。

依据“岁月”号客船向一侧倾覆的视频,可以判断“岁月”号客船沉没的原因是该客船在沉没瞬间承受着巨大的偏心力,这个巨大的偏心力是船上的集装箱等物品的不均匀荷载造成的,不均匀的荷载来源于货物的扎堆乱放。各类船只在启航前,运用幻立方构造的思路,将船上的集装箱堆成荷载对称于中心线的长方体颇有必要。

幻立方的构造方法比较复杂[7-9],多重幻方是一个典型的NP难题[10-12],利用计算机搜索幻方的时间复杂度是超乎人们想象的。

1 基本思路

本文的3t+1阶幻立方的构造可概括为以下几个步骤。

步骤1 将S=[1,2,3,…,n3]中的n3个自然数按顺序依次填入n×n×n立方体的n个截面上,使得n个截面上出现n×n个沿水平线排列的级数序列和n×n个沿垂线排列的级数序列,从而形成n×n个级数序列的n个划分----方阵B(1),B(2),…,B(n)。

步骤2 将方阵B(1),B(2),…,B(n)各划分成4个子矩阵:1个t×t方阵,1个(2t+1)×(2t+1)方阵,2个长方矩阵为t×(2t+1)和(2t+1)×t阶的。

步骤3 令2个长方矩阵中的2t个序列与(2t+1)×(2t+1)方阵中的2t个序列相互置换,令t×t方阵中的t×t个自然数重新排列成一个幻方,即得3t+1阶幻立方的10个幻方M(1),M(2),M(3),…,M(10)。

2 取t=3的10阶幻立方

下面是10阶幻立方的构造步骤。

步骤1 将S=[1,2,3,…,1 000]中的1 000个自然数按顺序依次填入10×10×10立方体的10个截面上,使得10个截面上出现10×10个沿垂线排列的级数序列,从而形成10×10个级数序列的10个划分----方阵A(1),A(2),…,A(10)。

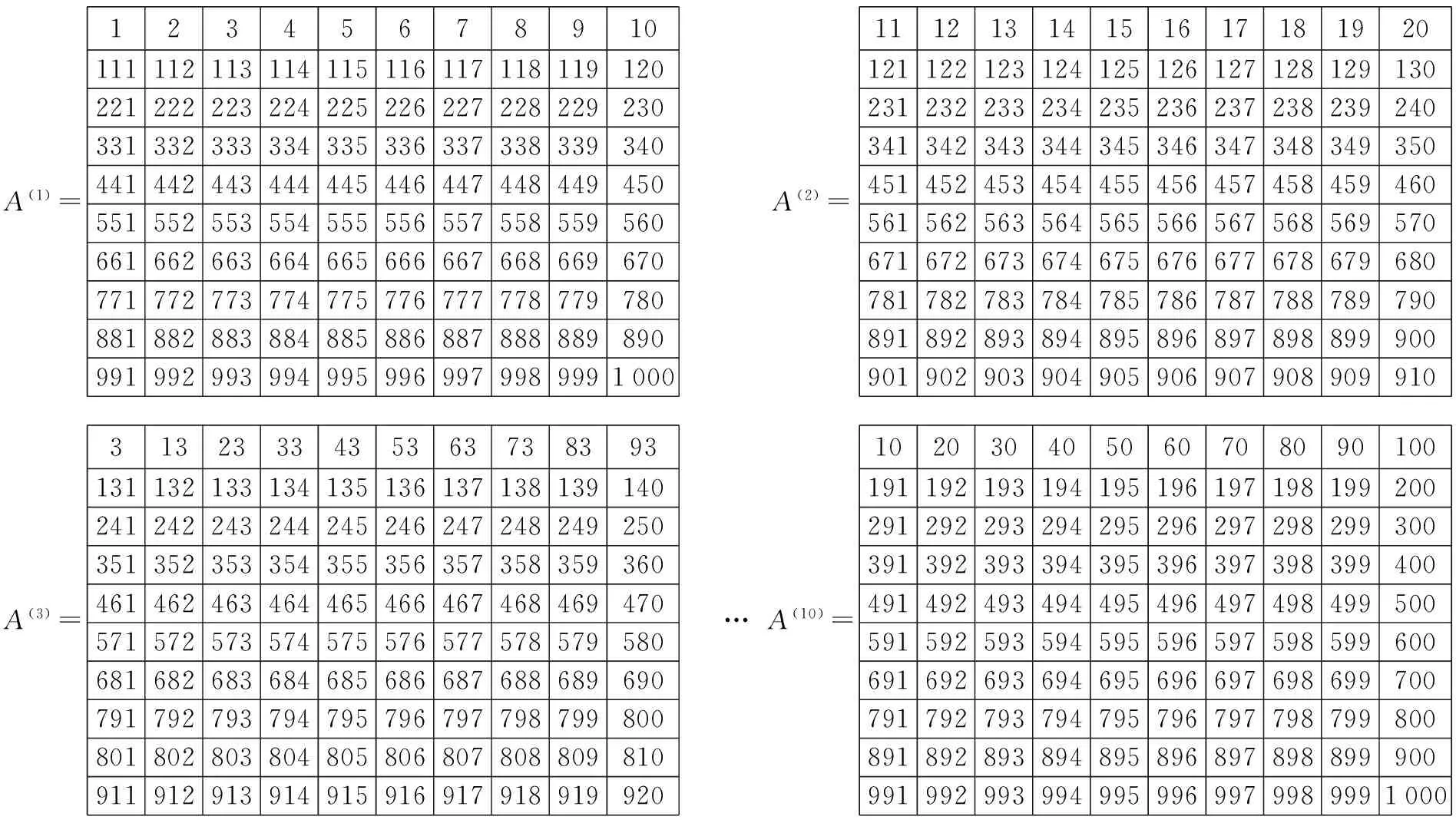
A(1)=123456789101111121131141151161171181191202212222232242252262272282292303313323333343353363373383393404414424434444454464474484494505515525535545555565575585595606616626636646656666676686696707717727737747757767777787797808818828838848858868878888898909919929939949959969979989991000A(2)=11121314151617181920121122123124125126127128129130231232233234235236237238239240341342343344345346347348349350451452453454455456457458459460561562563564565566567568569570671672673674675676677678679680781782783784785786787788789790891892893894895896897898899900901902903904905906907908909910A(3)=3132333435363738393131132133134135136137138139140241242243244245246247248249250351352353354355356357358359360461462463464465466467468469470571572573574575576577578579580681682683684685686687688689690791792793794795796797798799800801802803804805806807808809810911912913914915916917918919920 …A(10)=1020304050607080901001911921931941951961971981992002912922932942952962972982993003913923933943953963973983994004914924934944954964974984995005915925935945955965975985996006916926936946956966976986997007917927937947957967977987998008918928938948958968978988999009919929939949959969979989991000

步骤2 将方阵A(1),A(2),A(3),…,A(10)各划分成4个子矩阵:1个7×7方阵,1个3×3方阵,2个长方矩阵为3×7和7×3阶的。

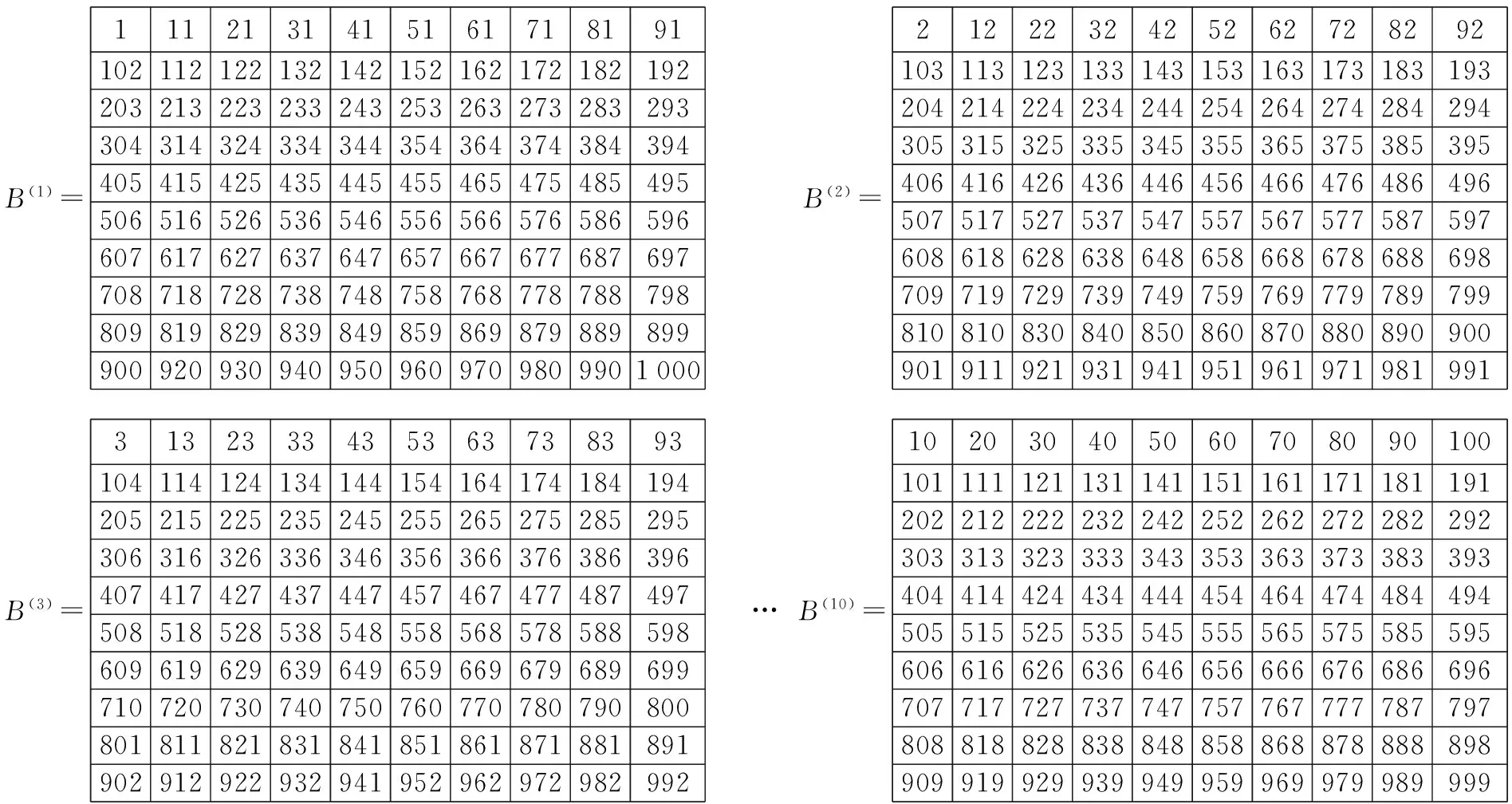
B(1)=11121314151617181911021121221321421521621721821922032132232332432532632732832933043143243343443543643743843944054154254354454554654754854955065165265365465565665765865966076176276376476576676776876977087187287387487587687787887988098198298398498598698798898999009209309409509609709809901000B(2)=2122232425262728292103113123133143153163173183193204214224234244254264274284294305315325335345355365375385395406416426436446456466476486496507517527537547557567577587597608618628638648658668678688698709719729739749759769779789799810810830840850860870880890900901911921931941951961971981991B(3)=3132333435363738393104114124134144154164174184194205215225235245255265275285295306316326336346356366376386396407417427437447457467477487497508518528538548558568578588598609619629639649659669679689699710720730740750760770780790800801811821831841851861871881891902912922932941952962972982992 …B(10)=102030405060708090100101111121131141151161171181191202212222232242252262272282292303313323333343353363373383393404414424434444454464474484494505515525535545555565575585595606616626636646656666676686696707717727737747757767777787797808818828838848858868878888898909919929939949959969979989999

步骤3 令7×7方阵中3条线上的序列与右侧长方矩阵中3条垂线上的序列相互置换;令7×7方阵中的另外3条线上的序列与左下长方矩阵中的3条水平线上的序列相互置换;令7×7方阵中剩余线上的7个数保持原位不动;令3×3方阵中9个自然数重新排列成幻方,最后,得10阶幻立方的10个幻方M(1),M(2),M(3),…,M(10)。

M(1)=16975864757188399603642431229701129168757672884940535423385991022319281679738516465344748869920334293182716275064551727588099304453942833161756638427376881994055649514221607596485374708829950667253132112133244355466576110277888910004255366475116220331488998078863741152263304415526990798879M(2)=26985874767198409613652441239611139268857772985040635523486090122419382678739517466345749870911335294183726285074561737598109214463952843261856758527476982093155749614322608597486375709830941668254133122143254365476586210377989099142653764854216320431590097178963842153264305416527981799880M(3)=3699588477720841962366245124962114936895787308414073562358519022251948367974051846734675086191233629518473629508457174760801922447396285336195683862757708119325584971442360959848737671082194266925513413215326437548659631047808819924275386495316420531689197279063943154265306417528982800871M(4)=4700579478711832953367246125963115946905797218424083572368529032261958468073151946834774186291333729618574630509458175751802923448397286346205693872767618129335594981452461059948837770182294367025613514216327438549660641057718829934285396505416520631789297378164044155266307418529983791872M(5)=5691590479712833954368247126964116956815807228434093582378539042271968567173252046934874286391433829718675621510459176752863924449398287356115703882777628139345604991462560160048937670282394466125713615217328439550651651067728839944295406415511620731889397478263145156267308419530984792873M(6)=6692581480713834955369248127965117966825717238444103592388549052281978667273351147034974386491533929818776622501460177753804925450399288366125613892787638149355515001472660259149037970382494566225813716218329440541652661077738849954365316425616720831989497578363246157268309420521985793874M(7)=769353247171483595637024912896611897683572724845401360239855906229198876737345124613507448659163402991887762350245117875480592644140028937631562390279764815936552491148276035924813807048259466632591381721933043154265367108774885996421532635716820932089597678463347158269310411522986794875M(8)=8694583472715836957361250129967119986845737258464023512408569072301998867473551346234174586691733130018978624503452179755806927442391290386145633812807658169375534921492860459348237170582694766426013918220321432543654681097758869974225336445816921031189697778563448159270301412523987795876M(9)=9695584473716837958362241130968120996855747268474033522318579082212008967573651446334274686791833229119079625504453180756807928443392281396155643822817668179385544931502960559427137270682794866525114019211322433544655691107768879984235346455917020131289797878663549160261302413524988796877 …M(10)=106965854747178389593632421219691211006865757278484043532328589092221919067673751546434374786891933329218180626505454171757808929444393282406165653832727678189395554941413060659548437370782894966625213120212323434545656701017778889994245356466016120231389897978763650151262303414525989797878

以上所得的幻立方矩阵系2D幻方矩阵,倘若将该立方矩阵实施下列措施:1)令矩阵M(1)中的10个序列保持原位;2)令矩阵M(2)中的10个序列上移1个行距;3)令矩阵M(3)中的10个序列上移2个行距;4)令矩阵M(4)中的10个序列上移3个行距;…;10)令矩阵M(3)中的10个序列上移9个行距,则得10阶3D幻立方的10个幻方C(1),C(2),C(3),…,C(10)如下:

C(1)=16975864757188399603642431229701129168757672884940535423385991022319281679738516465344748869920334293182716275064551727588099304453942833161756638427376881994055649514221607596485374708829950657253132112133244355466576110277888910004255366475116220331488998078863741152263304415526990798879C(2)=9611139268857772985040635523486090122419382678739517466345749870911335294183726285074561737598109214463952843261856758527476982093155749614322608597486375709830941668254133122143254365476586210377989099142653764852163204315900971789638421532643054165279817998802698587476719840951365244123C(3)=8519022251948367974051846734675086191233629518473629508457174760801922447396285336195683862757708119325584971442360959848737671082194266925513413215326437548659631047808819924275386495316420531689197279063943154265306417528982800871369958847772083195236624512496211493689578730841407356235C(4)=7418629133372961857463050945817575180292344839728634620569387276761812933559498145246105994883777018229436702561351421632743354966064105771882993428539650541652063178929737816404415526630741852998379187247005894787118329533672461259631159469057972184240835723685290322619584680731519468347C(5)=3882777628139345604991462560160048937670282394466125713615217328439550651651067728839944295406415516620731889397478263145156267308419530984792873569159047971283395436824712696411695681580722843409358237853964227196856717325204693487428639143382971867562151045917675280392444939828735611570C(6)=3892787638149355515001472660259149037970382494566225813716218329440541652661077738849954365316425616720831989497578363246157268309420521985793874669258148071383495536924812796511796682571723844410359238854905228197866727335114703497438649153392981877662250146017775380492545039928836612561C(7)=5924813807048259466632591381721933043154265367108774885996421532643571682093208959767846334715826931041152298679487576935824717148359563702491289661189768357272484540136023985590622919887673734512461350744865916340299188776235024511787548059264414002893761356239027976481593655249114827603C(8)=2203214325436546810977588699742253364458169210311896977785634481592703014126239877968768694583472715836357361250129967119986845737258464023512408569072301998867473551346234174586691733130018978624503452179755806927442391290386145633812807658169375534921492860459348237170582694766426013918C(9)=42353464559170201312897978786635491602613024135249887968779695584473716837958362241130968120996855747268474033522318579082212008967573651446334274686791833229119079625504453180756807928443392281396155643822717668179385544931502960559448337270682794866525114011921132243354465569110776887998 …C(10)=636501512623034145259897978781069658547471783895936324212196911110068657572784840435323285890922219190676737515464343747868919333292181806265054541717578089294443932824061656538327276781893955549414130606595484373707828949666252131202123234345456567010177788899942453564660161202313898979787

3 结 语

本文的贡献是:1)发现了3t+1阶幻立方的构造方法;2)构造出10阶幻立方的10个幻方M(1),M(2),M(3),…,M(10);3)解决了N阶幻立方的计数问题。作者的期待是让幻立方的基本思路在集装箱运输领域及其他更多领域中得到广泛的应用[13]。

[ 1 ]DENES J. Latin squres and their application[M]. Budapest:Akademiai kiado, 1974.

[ 2 ]杨富锋. 构造奇次同心幻方的一种方法[J]. 数学的实践与认识, 2006,36(5):192-199.

[ 3 ]杨骅飞,王朝瑞. 组合数学及其应用[M]. 北京:北京理工大学出版社, 1992.

[ 4 ]曹小琴,高治源,周玮媛. 用两个正交拉丁幻方构造2n+1阶完美幻方的一种简便方法[J]. 宁夏大学学报(自然科学版), 2004,25(2):119-123.

[ 5 ]汪潘义. 偶数阶幻方矩阵行列式的研究[J]. 合肥学院学报(自然科学版), 2010,20(1):23-26.

[ 6 ]欧阳录. 最佳拉丁方与高级原幻方[J]. 数学理论与应用, 2001,21(3):22-28.

[ 7 ]俞万禧. 20阶正交拉丁方的构造[J]. 淮南工业学院学报, 2000,20(3):55-60.

[ 8 ]俞万禧. 3t+1阶正交拉丁方构造的新方法----图表法[J]. 矿业科学技术, 2001,29(4):45-50.

[ 9 ]刘玉君. Turbo码中幻方交织器的研究与设计[J].信息工程大学学报, 2006,7(4):291-395.

[10]祝宝满,龚和林. 非素数阶幻方的构造[J]. 数学的实践与认识, 2008,38(15):207-214.

[11]陈剑南. 素数阶均衡完美幻方若干问题初探[J]. 计算机工程与应用, 2005,45(21):179-182.

[12]姜伟,刘彦佩. 几类4-正则平面图的最小折数纵横扩张[J]. 沈阳师范大学学报(自然科学版), 2007,25(2):129-134.

[13]欧阳录. 幻方与幻立方的当代理论[M]. 长沙:湖南教育出版社, 2004.

Amethodofconstructingmagiccubesoforder2t+1

CHOUWanxi1,MENBo2

(1. School of Civil Engineering and Architecture, Anhui University of Science and Technology, Huainan 232001, China; 2. College of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)

The problem of magic cubes is introduced. The characteristics of equilibrium structure of magic cubes is clarified in this paper. The application value of magic cubes is pointed out by analyzing the reason of a ship sank. A method to construct 3t+1 order magic cubes is discovered. The basic procedure of constructing 3t+1 order magic cubes is described. The procedure of constructing 3t+1 order magic cubes is presented. According to this construction steps, the procedure of constructing 10 order magic cubes is given fort=3 and the corresponding rusults to each step is obtained. Finally, 10 magic cubes of 10 order magic cube is obtained and the enumeration problem of 3t+1 order magic cube is solved.

magic cubes; construction;enumeration proble

2017-05-16。

国家自然科学基金资助项目(11201313)。

侴万禧(1930-),男,辽宁大连人,安徽理工大学教授。

1673-5862(2017)04-0461-05

O157

A

10.3969/ j.issn.1673-5862.2017.04.016