高分子链移位动力学的理论和模拟研究

2017-12-26吴凡罗孟波

物理学进展 2017年6期

关键词：链节势阱构象

吴凡，罗孟波

浙江大学物理系，杭州，310027

高分子链移位动力学的理论和模拟研究

吴凡，罗孟波∗

浙江大学物理系，杭州，310027

高分子链通过纳米管道或纳米孔的移位，存在于各种生命过程中，是物理、化学和生物领域的重要课题，在实验、理论和计算机模拟等领域已经被广泛研究，并应用于科技的不同领域。本文总结了高分子链移位的理论和模拟方面的最新研究成果，讨论了自由能形貌对高分子链移位动力学过程的影响。结合理论计算和模拟研究，分析了链与管道的相互作用、链的组分、链节电荷分布、管道的性质等因素对自由能形貌和高分子链移位时间的影响，并结合自由能形貌对研究结果进行了解释。研究结果有助于理解高分子链的移位机制，从而进一步调控高分子链的移位时间。

高分子链；纳米孔；纳米管道；移位；计算机模拟

I.引言

近二十年来，高分子（包括聚电解质、蛋白质、DNA等链状大分子）通过纳米孔的跨膜移位问题引起了人们的广泛关注。一方面是由于这个过程常见于生物体内的生命过程，如RNA穿过细胞核孔，DNA由病毒进入宿主细胞，蛋白质进入内质网，基因在细菌之间的传输等；另一方面则是由于该过程具有广阔的应用前景，如快速DNA测序、分子检测、基因治疗、可控药物运输以及设计纳米孔检测设备等[1,2]。纳米孔可以实现对单分子的非标记分析，也因此有望成为下一代DNA的测序工具，提供廉价、快速和高通量的DNA检测和分析。高分子穿过纳米孔或纳米管道这一课题已成为近20年来理论、模拟和实验研究的重要内容之一[3,4]。高分子链穿孔过程是一个复杂的非平衡态动力学过程，其中高分子链的熵和无规热运动是两个重要的影响因素，因此也是软物质物理的一个重要研究对象[3,5,6]。

1996年Kasianowicz等发现DNA链可以在电场的驱动下穿过α-溶血素（alpha-hemolysin，简称α-HL）蛋白纳米孔/管道。当 DNA通过α-HL管道的时候，管道内的DNA阻碍了溶液离子的通路，导致离子电流明显下降[7]。从电流的变化可以辨别一条DNA链在电场驱动下通过α-HL管道的过程，并据此测量DNA链通过管道的移位时间。基于利用纳米管道进行DNA的测序和分离的思想，纳米孔/管道技术作为一种重要的高分子生物检测方法引起了广泛的关注。常用的纳米管道有三类：以α-HL为代表的蛋白质管道、固态材料纳米管道、以及多组分材料（蛋白质+固态材料、固态 +固态材料等）组成的复合管道 (compounded channel)[2,4]。后二者可以结合半导体材料，可应用于高通量快速的光电检测，是纳米管道技术未来发展的主要方向[2]。利用纳米孔/管道技术进行高分子生物检测有了明显的进展，最近的实验表明利用α-HL管道可以区分聚乙二醇[分子式HO(CH2CH2O)nH]分子中单体CH2CH2O的数目[8]和利用人造纳米固态孔可以区分DNA和RNA[5]。虽然目前尚不能区分一条DNA链上的单个核苷酸及序列，但利用纳米管道却可以区分一条链上的DNA片段和蛋白质片段[9]，也可以通过修饰α-HL管道区分不同的核苷酸聚集体[10]。目前，有关石墨烯和碳纳米管道这类固态纳米孔的研究也正在迅速发展中[11−13]。带电的寡核苷酸等生物分子在电场驱动下进入碳纳米管时，会影响通过碳纳米管的离子流量，引起电流的变化。通过观察特定的电流信号，可以实现对生物分子的检测[12]。目前固态纳米管道由于具有结构稳定、尺寸可调、表面可修饰等优点而越来越受到关注[6]。例如，通过对固态管道内部的生化选择性修饰可以更好地检测分子的性质[14]。

利用纳米孔实现高分子检测的关键是控制高分子链在纳米孔中的运动[15,16]。现在实验上的主要困难可以归纳为以下两个：（1）高分子移位速度快，例如典型的DNA链穿过α-HL管道时每个核苷酸的平均时间是µs量级，现有仪器难以分辨单个核苷酸的运动[7]；（2）高分子移位中存在大的热噪声[17]，热噪声导致高分子运动的速度和方向随机变化。虽然可以通过增大孔的摩擦来减缓高分子的移位速度和降低温度来抑制热噪声，但目前效果不佳[17,18]。最近的实验研究发现，利用原生的气溶素(aerolysin)纳米孔可以使DNA链的移位速度降低约3个数量级，原因是这种孔与DNA有强烈的静电吸引作用[19]。另外，研究发现复合管道的界面可以产生自由能势阱，从而增加高分子链的移位时间[20−22]。复合管道的内表面至少包含两种不同性质的成分，可以通过表面修饰、外电场调控、不同管道材料复合等方法实现[22,23]。复合管道的不对称也可以使自由能倾斜产生棘轮(ratcheting)作用，使高分子链产生定向运动[24]。这些研究表明有可能通过设计合适的管道来控制高分子移位运动的速度。

理论研究通常根据高分子链穿孔/管道过程的自由能形貌(free-energy landscape)采用Fokker-Planck方程计算链的移位时间[25,26]。自由态高分子链的构象熵大于穿孔时受限态高分子链的构象熵，导致高分子穿孔时自由能上升。自由能势垒使高分子穿孔的概率下降，导致穿孔事件不容易发生。即使有部分高分子链的链节穿过了小孔，这些链节也常常因为自由能势垒而全部退出小孔，导致穿孔事件的失败。自由能形貌还跟高分子受到的驱动力和高分子与孔的相互作用有关。一般来说，驱动力倾斜自由能，使势垒降低并在孔两侧产生一个自由能差，导致高分子穿过小孔的概率增大和移位时间的下降。高分子受到的驱动力可以是电场力，也可以是孔两侧的化学势差等。另外，高分子与孔的相互吸引降低自由能，可以把由于构象熵减小引起的自由能势垒改变为自由能势阱，而自由能势阱越深则高分子链的移位时间越长[20,27,28]。调节自由能势阱的深度可以大幅改变高分子链的移位时间，是一种较理想的物理方法。Fokker-Planck方程计算和计算机模拟均得到高分子链的移位时间与自由能形貌有关的结论[20,25]。

但因为高分子链移位是一个非平衡态问题，所以基于平衡态自由能概念的Fokker-Planck方程并不完全适用于描述高分子链的移位过程和规律[29]。然而，利用自由能形貌可以预测高分子链的移位时间，因此Fokker-Planck方程和自由能形貌在理论分析中仍然发挥着重要作用[20,27,30]，能使我们快速定性地理解高分子链的移位规律。但要得到精确的移位规律、理解物理机制仍需要借助于大规模的计算机模拟研究。目前，计算机模拟已经成了研究高分子链穿孔的一个重要手段，在研究高分子链移位现象背后隐藏的深层次基本问题和规律上起了非常重要的作用[31−35]。计算机模拟可以直接得到高分子链穿孔过程的微观和宏观信息，提供定量的移位信息，获得普适性的一般规律。

本文第二部分介绍高分子链模型和计算机模拟方法；第三部分介绍研究高分子移位时间的理论方法；第四部分介绍高分子移位的一些研究成果，主要讨论自由能形貌对高分子移位的影响，以及链与管道的相互作用，管道的长度和构成，驱动力等因素对高分子移位的影响。

II.高分子链的统计模型及模拟方法

线形高分子 (polymer)或者大分子 (macromolecule)是由大量（约 103∼105数量级）重复结构单元键合而成的长链状分子。高分子链的构象数随高分子链的长度（即单元数）指数增加，构象数目庞大。计算机模拟研究通常采用抽样统计的方法计算高分子链统计性质的近似平均值。根据重整化群理论，高分子链大尺度的统计性质与高分子链的具体细节无关。因此可以对高分子链进行粗粒化处理，忽略实际高分子的大量不必要的细节结构，仅抽取高分子的本质结构，从而充分降低了体系的自由度，节约计算机模拟的时间。早期的正四面体（或金刚石）格点模型就是只保留了聚乙烯的主链骨架碳原子。现在常用的简化模型是粗粒化模型，把高分子链看作是由粗粒化粒子（通常称之为链节）顺序连接而成的链，其中的每个链节可以代表多个骨架原子，而连接链节之间的键也就不是通常意义上的化学键。Kuhn链模型是一种典型的粗粒化模型，它把真实的高分子链用等效自由连接链来描述。

在粗粒化模型中，根据链节位置在空间取值连续与否可以将高分子链分为格子链和非格子链。格子链模型将空间离散化，高分子的链节只能落在格子的格点上。格子链的这种离散化处理与真实链的运动细节有较大的差别，但这并不影响高分子链的大尺度性质的统计。其中，简立方格子链是最常用的格子模型。根据键长的不同，简立方格子链又分为固定键长链和键长涨落链。在固定键长的链模型中，键连链节之间的距离保持恒定（取简立方格子的边长）；在键长涨落模型中，键连链节之间的距离可以取若干个离散的值。在格子模型中，常常计入自回避(self-avoiding)和最近邻相互作用来模拟更真实的高分子链。自回避是指高分子的两个链节不能同时占据同一个格点，体现了高分子链节的排斥体积效应(excluded volume eあect)。格子上自回避行走（self-avoiding walk，简称 SAW）高分子链模型是高分子链的重要模型，在高分子理论和模拟中发挥了非常重要的作用。当进一步考虑高分子链节之间的远程范德华尔斯作用的时候，模拟引入了链节之间的最近邻相互作用E，即当两个非键连的链节位于最近邻的两个格点上的时候引入相互作用E。最近邻相互作用的引入大大丰富了格子链模型的物理内涵。

非格子链中，高分子链上所有链节的位置可以在空间连续取值，因此能比较真实地反映高分子链的构象变化特点。理论分析常用的非格子链模型有自由连接链（freely jointed chain），自由旋转链（freely rotational chain），和高斯链（Gaussian chain）。计算机模拟中则常用考虑了多种相互作用的珠簧链（beadspring chain），如键能、弯曲能、远程Lennard-Jones(LJ)相互作用等。典型的键能是有限扩展的非线性弹性（ fi nite extensible nonlinear elastic，简称FENE）势

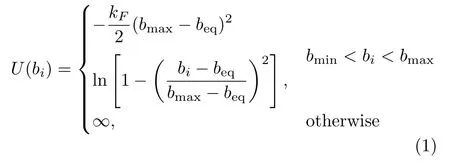
其中键长bi限制在最小键长bmin=2beq−bmax和最大键长bmax之间，beq是平衡键长，kF是FENE弹性系数。FENE势限制了高分子链中的键长，在高分子动力学的研究中应用广泛[36]。相邻两个键的键角为θ，高分子链考虑一定的刚性，键角弯曲能为

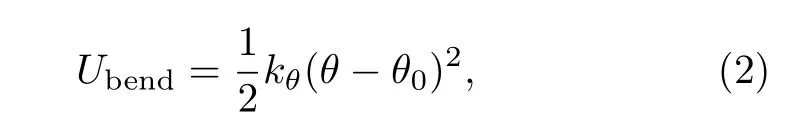
其中kθ和θ0分别是刚性系数和平衡键角，kθ=0代表柔性链，而kθ＞0代表半刚性链。模拟中平衡键角θ0常取为π，此时两个键取伸展的直线状态。高分子中非键连的链节之间的相互作用采用截断的LJ势

其中rij是链节i,j之间的空间距离，εij是链节i,j之间的相互作用强度，相互作用的截断距离为rcut。

高分子移位的计算机模拟常采用这些粗粒化的高分子模型，模拟高分子移位的动力学过程的模拟方法主要是动力学Monte Carlo方法和朗之万(Langevin)动力学方法。

A.动力学 Monte Carlo方法

在动力学Monte Carlo方法中，高分子链的整体运动通过高分子链节的局域移动来实现。高分子链节的局域运动导致高分子链构象的变化，这种构象变化可以通过构造一个Markov过程来实现，即假定高分子链原来处于构象{→r}，通过链节运动以一定的转移概率P({→r}→{→r′}) 得到新的构象{→r′}。链节局域运动成功与否通常采用Metropolis算法决定，即该转移概率P取P=min[1,exp(−ΔE/kBT)][37]，其中 ΔE是构象转变前后的能量差，即这里kB是Boltzmann常数，T是温度。具体的计算机模拟过程如下：

1.随机构造高分子链（长度为N）的初始构象；

2.随机选择高分子链的一个链节i；

3.对于格子链模型，随机选择链节i所在位置的近邻格点作为链节i的新位置；对于非格子链模型，链节i的位置 (xi,yi,zi)在x、y、z方向分别随机改变 dx、dy、dz，从而达到一个新位置如果链节i的新位置不满足模型条件（如：排斥体积条件、键长限制条件、键不交叉条件等），则放弃链的运动而重新回到步骤2；

4.如果链节i的新位置满足模型条件，则计算由于链节i的运动引起的能量变化值ΔE；

5.随机生成一个 [0,1)区间内的随机数r，若r≤min[1,exp(−ΔE/kT)]，则接受链节i新位置，否则返回到步骤2；

6.重复步骤2−5，直到满足预先设定的终止条件。

在Monte Carlo模拟中往往定义高分子链链节的N次尝试运动为一个Monte Carlo步长，并作为模拟的时间单位。

Metropolis方法适合于格点链和非格点链模型。对于格点链，高分子链节每次运动一个格子长度。对于非格点链，高分子链节在x，y和z方向分别运动dx,dy和 dz，其中 dx,dy和 dz是介于 (−Δ,Δ)之间的随机量。Δ的值要根据模型合理选取，使模拟的接受率在一个合理的范围内。

B.Langevin动力学模拟

Langevin动力学模拟高分子链的运动时把溶剂看成背景，这样可以简化模拟系统并加快模拟速度。溶剂分子与高分子的随机相互作用提供模拟系统的随机力，高分子运动带动溶剂分子的运动表现为高分子链受到溶剂的粘滞力。这两个力一起参与调节高分子的运动，并达到对整个系统能量的调控，即调控系统温度，压强等。高分子链节之间的远程相互作用也包含了溶剂的作用，如良溶剂、不良溶剂反映在高分子链节之间的不同远程相互作用。

高分子链节的运动方程为

其中U包含键能、刚性能和链节之间相互作用等所有势能，→F(T)是热运动随机力，−η→vi是粘滞力，→f是大分子链受到的其他驱动力。例如，在管道中的带电高分子链受到电场的驱动。考虑到管道的尺寸很小，物理上可以简化为只在管道中存在电场→E和电场力→f=q→E，q是链节的电荷，与链节的性质有关。链节的位置和速度的演化过程通常采用修正的velocity-Verlet算法，这种算法可以用以下的迭代方程

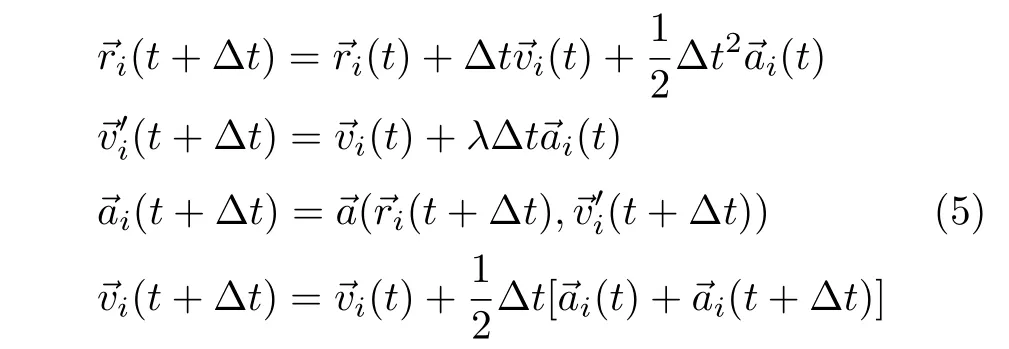
描述，其中→a,→v和→r分别是加速度、速度和位置。参数λ常取为0.65[38]。t和 Δt分别是模拟时间和迭代的时间步长。链节的加速度→a=Σ→F/m，其中Σ→F是链节受到的合力，m是链节质量。

模拟中的物理量均是约化的无量纲量，我们取长度单位σ=1，质量单位m=1，和能量单位kBT=1。模拟的时间单位为τ=(mσ2/kBT)1/2，力的单位是kBT/σ。

III.高分子移位时间的理论方法

高分子链从cis空间经过小孔到达 trans空间的移位时间除了计算机模拟外，也可以通过理论计算得到。小孔的尺寸远小于高分子链的尺寸（如高分子链回转半径RG），如图1所示。链长为N的高分子链有N+1个链节，链节编号从0到N。高分子链通过小孔的时间较长，可把高分子链的移位过程近似为准平衡态过程。

图1.高分子链穿过小孔不同时刻的构象示意图：（A）进入小孔，（B）穿孔中，（C）离开小孔。

根据 Sung和 Park以及 Muthukumar的理论，高分子链穿过管道的过程可用Fokker-Planck方程表示[25]：

其中，Px(t)表示t时刻高分子处于状态x的概率，F(x)是状态x的高分子自由能，D表示高分子链的扩散系数，b是高分子沿孔前进或后退一步的长度。这里高分子的状态用链进入trans空间的长度x或链节数m表示，x=mb。高分子链穿过小孔的过程表现为从状态x=0变为x=Nb。

根据高分子链的自由能形貌F(x)可求出高分子穿孔的时间，但方程的解还与边界条件有关。研究中常用到两种边界条件：一是反射吸收边界条件，二是双吸收边界条件。当考虑反射吸收边界条件，进入小孔的高分子链不能重新返回到cis空间，而当高分子进入trans空间时则被完全吸收，穿孔过程结束，这样高分子链穿过小孔所用时间为：

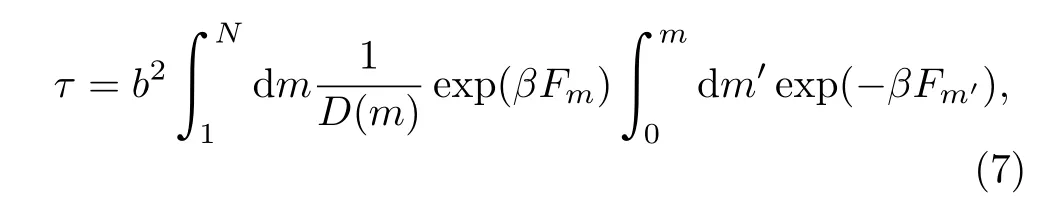
这个时间称为首次通过时间( fi rst passage time)[25]。计算中假定移位过程中的扩散系数D(m)是一个常数D，并用b2/D作为时间单位。而考虑双吸收边界条件时，进入小孔的高分子链可以重新返回到cis空间，高分子完成一次失败的穿孔。在经过多次失败以后，高分子链最终完成一次成功的穿孔。高分子链最终成功穿过小孔所用的时间称为移位时间(translocation time)，而用于失败的穿孔的时间是不记入移位时间的。这样定义的移位时间与实验测量到的DNA分子的移位时间（即电流下降的时间）一致。移位时间的计算公式为[39]

自由能F可由下面公式得到：F=U−TS，其中S为高分子链的构象熵，U是内能。穿孔过程的高分子链可以看成相连的2段接枝链，高分子链的构象熵为2段接枝链的构象熵的和。对于自回避行走高分子链，长度为m的接枝链的构象熵近似为[26]

这里µ是高分子链节生长的有效配位数，γ是与高分子表面相关的指数。对于简立方格点上的自回避行走接枝高分子链，我们有µ=4.68和γ=0.69[40]。计算机模拟中，计算自由能常用以下两种方法：完全计数法和Rosenbluth-Rosenbluth法。完全计数法枚举高分子的所有构象，自由能可以通过

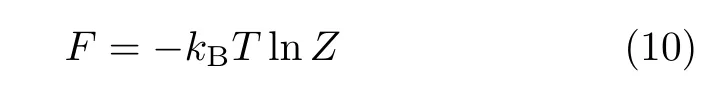
得到，其中

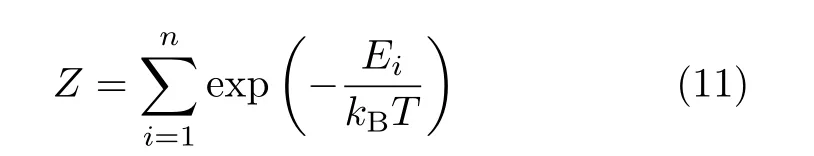
为高分子链的配分函数。完全计数法的优点是精确，但随着链长的增加，构象数随之指数增加，因此实现起来十分困难。Rosenbluth-Rosenbluth法模拟高分子生长过程中每一步的权重，可以很有效地排除概率极低的构象，大大节省了构象统计的时间，可以得到近似的自由能值[41,42]。考虑到驱动力，假定孔两侧的化学势差是 Δµ（trans侧与 cis侧的差），那么在自由能上再加上 (m+1)Δµ。Δµ＜0帮助链穿孔，反之Δµ＞0则阻碍链穿孔。如果是力f，那么化学势差可以写成Δµ=−fL，其中L是孔的长度。

利用Fokker-Planck方程研究高分子移位的理论将高分子链的移位简化为一个一维扩散问题，将移位时间的求解归结为自由能的求解。只要求出高分子链在移位过程每一步（每一状态）的自由能，即自由能形貌，那么就可以求出特定边界条件下的移位时间，这充分体现了自由能对高分子链移位这一物理过程的控制和主导。但由于该理论建立在高分子穿孔过程的准平衡态假设之上，只适合弱驱动、低扩散的情况[43]。大量的计算机模拟表明，高分子链经纳米管道的移位本质上属于非平衡态过程[29]。尽管理论计算定量上与模拟结果有差别，但基于自由能形貌的理论仍能很好地定性解释模拟结果[20]。

IV.高分子链通过管道移位的研究结果

高分子链模型是实验所用的单链DNA的物理模型，在解释DNA穿孔的实验结果方面起着重要作用。高分子链穿孔的计算机模拟在解释DNA穿孔过程的标度关系，提出DNA检测和分离的新方法，探索高分子链穿孔的新现象、新规律和新应用等方面发挥了重要作用[3]。

根据高分子和管道的不同性质，高分子链通过管道的移位可分为如下情况讨论：根据高分子链长和管道长度，可分为高分子链长比管道短的情况（N＜L）和高分子链长比管道长的情况（N＞L）；根据高分子链的组分，又分为均质链，嵌段高分子链以及部分带电高分子链等；根据管道性质，还能分为均匀管道，梯度管道，和复合管道等。高分子链通过管道的移位过程可以细分为充填( fi lling),转移(transferring)和逃离(escaping)三个分过程，如图2所示[24]。而高分子链的状态可以由4个特殊的状态，即如图2的A，B，C，D这4种状态，来表征。当N≫L时，可将管道当成小孔，此时取L=0。

图2.高分子移位的四个状态A，B，C，D和三个阶段：填充阶段(Filling stage)，转移阶段(Transferring stage)和逃离阶段 (Escaping stage)。具体分析时，根据高分子链长N和管道长度L的关系分成(1)N＞L和(2)N＜L两种情况。

模拟中常考虑狭窄的孔道，其孔道的大小与高分子链节的大小相当，因此假定高分子在孔道中顺序前进。我们可以用一维的虚拟位置坐标xv来描述高分子穿孔的位置，其中xv=0表示高分子的第一个链节到达孔道的最左端，如图2的状态A。我们进一步假定高分子沿孔道的中心线移动，因此虚拟位置坐标xv描述高分子穿孔过程中高分子在孔道中移动的距离。当高分子没有进入孔道前，xv＜0。高分子最后从孔道出来的时候，如图2的状态D，xv=N+L。为分析方便，这里取高分子键长为1。

A.均聚高分子穿孔

均聚高分子中所有链节都相同，是最简单的高分子链模型。均聚高分子在通过小孔的时候，高分子的构象熵下降。这时可以把高分子链看成 2段接枝链，如图1B所示。因此，高分子的穿孔可以看成从一个长度为N的接枝链演变为2段长度分别为N−m和m的接枝链，因此高分子链的构象熵下降量为[26]

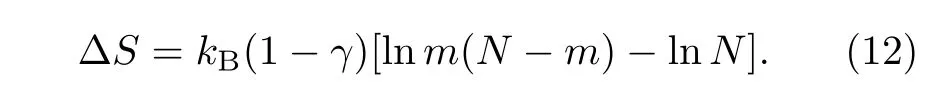
构象熵的下降导致自由能的升高，产生一个自由能势垒阻碍链的通过，表现为小的穿孔概率[44]。如果考虑高分子与孔的相互作用，或者引入与高分子有相互作用的分子伴侣，能改变高分子穿孔的自由能形貌[45]。在格点的计算机模拟中，高分子与孔的相互作用常取约化的最近邻相互作用ε=E/kBT。这里ε＞0表示高分子与孔排斥，ε＜0表示高分子与孔吸引。而分子伴侣通常用纳米硬粒子来表示，与高分子之间存在短程的排斥作用和远程的相互吸引作用。

对于较短的链，高分子穿孔的自由能可以通过完全计数法求得。Sun对简立方格点上的SAW高分子链在孔内不同位置的构象进行完全计数，得到高分子整个穿孔过程的自由能形貌[20]。高分子在穿孔时的位置用虚拟位置坐标xv表示，高分子自由能F与xv的关系见图 3。

图3.不同高分子链–孔相互作用强度ε的高分子链穿孔自由能F与高分子穿孔的虚拟位置坐标xv的关系。Fb表示势垒的高度，Fw表示势阱的深度，高分子链长N=20，链节浓度ϕc=0表示模拟系统中仅有1条高分子链。β=1/kBT。

从图3可以看到三种自由能形貌： (1)当高分子链与孔的相互作用为排斥或弱相互吸引时(ε∼0)，高分子在移位过程中碰到一个势垒，势垒的高度随着吸引能的增大而降低；(2)在临界高分子链–孔相互作用强度附近，势垒几乎为0，高分子自由穿孔；(3)当高分子链–孔相互作用为强相互吸引时(ε＜−1)，自由能形貌出现势阱，其深度随着相互吸引的增强而变大。

基于该自由能形貌，用反射吸收边界条件的 Fokker-Planck方程（公式 (7)）计算了高分子链的平均移位时间＜τ＞，结果如图 4。一个有趣的现象是高分子的移位时间与势垒的高度几乎无关。因此虽然小孔处的势垒会阻碍高分子进入小孔，使得移位成功的概率下降，但不影响真正成功的移位过程的时间。高分子链跨膜移位的过程类似于一队人通过一个坡。势垒小对应于平坦的坡，运动快和运动慢的都能通过，因此平均通过的时间长；而势垒大对应于陡的坡，只有运动足够快的才能成功通过，而运动慢的注定失败[46]，因此平均通过的时间反而短。这使得高分子跨膜移位时间τ并没有想象中的随势垒高度的增大而增大，而是随势垒高度的增大而下降。相反，若在小孔处是一个势阱，虽然高分子受到孔的吸引而容易进入小孔，但陷入势阱后，却很难离开，因此移位时间会因为势阱的存在而变长。罗开富通过Langevin动力学研究发现管道的壁与高分子的相互吸引越强，高分子的移位成功率越高，但同时移位时间也越长，这一结果符合从自由能形貌出发的推测[44],也与Monte Carlo的模拟结果一致[28]。最近的实验发现，原生的气溶素纳米孔与DNA有强的静电相互作用，从而使DNA的移位速度降低约3个数量级[19]，这也与图4的模拟结果相符。

图4.高分子链的移位时间＜τ＞与高分子链–孔相互作用强度 ε的关系。高分子链长 N=20，链节浓度 ϕc=0，0.1和0.2。插图是高分子穿过相互作用小孔的示意图。

模拟研究表明，在不同高分子链–孔相互作用强度ε下高分子链的移位时间与链长的标度关系

在长链成立，但标度指数α与相互作用强度ε有关[21]。对于弱驱动，α从排斥相互作用的2.48降低到强吸引作用的2.35；而对于强驱动，α从排斥相互作用的1.35降低到强吸引作用的1.22[21]。

除了孔与高分子的相互作用可以改变高分子链穿孔的自由能形貌以外，还有许多因素能改变高分子链穿孔的自由能形貌。例如，高分子链节在cis空间中的链节浓度的升高能提高高分子链在cis空间的自由能，使高分子在小孔两边产生自由能差，从而减小高分子链的移位时间[28]。

同样，在cis空间的分子伴侣也能产生高分子在小孔两边的自由能差。分子伴侣的密度越大，自由能差也越大。这相当于分子伴侣对高分子的移位过程产生一个外加的驱动力，从而减小高分子的移位时间[45,47]。但当分子伴侣密度太大的时候，高分子的扩散减慢，反而使移位时间增大[47]。

研究较多的是trans空间的分子伴侣，因为生物细胞中含有大量类似于分子伴侣的溶酶体、脂滴、核糖体和线粒体等基团。高分子移位时间除了与分子伴侣的密度有关外，还与分子伴侣与高分子的相互作用、分子伴侣的流动性有关。当分子伴侣与高分子有较强的吸引时，trans空间中的分子伴侣可以降低高分子在trans空间的自由能，从而有助于高分子链的移位。但模拟表明，如果分子伴侣是静止的，分子伴侣对高分子的吸引同时减慢了高分子的扩散，这将阻碍高分子链的移位。综合这两个因素，模拟发现高分子的移位时间在适当的相互吸引强度下达到极小值[47,48]，如图5所示。

图5.高分子平均移位时间＜τ＞与分子伴侣与高分子的相互作用εt的关系。分子伴侣密度ϕt定义为分子伴侣的体积分数。高分子链长N=100，孔两侧化学势差Δµ=−0.5。τ0是高分子在没有分子伴侣的情况下的移位时间。插图是高分子链穿孔进入拥挤空间的示意图。

但trans空间中的分子伴侣的流动性对高分子移位时间的影响比较复杂。计算机模拟中分子伴侣的流动性V表示分子伴侣在一个Monte Carlo步长中平均移动的次数。若V=0，则分子伴侣静止；若0＜V＜1，则分子伴侣在一个Monte Carlo步长内有V的概率移动一个格点，若V≥1，则分子伴侣在一个Monte Carlo步长内平均移动V次。模拟结果表明存在一个临界流动性V∗，当V＜V∗时移位时间＜τ＞随V幂律增加，而当V＞V∗时移位时间＜τ＞随V幂律下降，见图6所示[49]。这个结果表明，缓慢运动的分子伴侣阻碍高分子的移位，但激烈运动的分子伴侣反而帮助高分子的移位。激烈运动的分子伴侣容易带动高分子的运动，增加了高分子的运动性。而缓慢运动的分子伴侣结合了高分子链以后，却降低了高分子的运动性。当然，这一结果只在相互吸引强度足够大的时候才起作用，因为强吸引作用会使高分子和分子伴侣的接触数增加。

图6.高分子平均移位时间＜τ＞与分子伴侣流动性 V的关系。（a）相互吸引强度 ε= −1.5，分子伴侣密度 ϕt不同；（b）分子伴侣密度 ϕt=0.01,相互吸引强度 ε=−1.5和ε=−1.7。高分子链长N=100，孔两侧化学势差Δµ=−0.5。

B.嵌段高分子穿孔

DNA是由一系列脱氧核苷酸构成的线形高分子链，其中组成脱氧核苷酸的碱基有腺嘌呤 (A)、鸟嘌呤 (G)、胞嘧啶 (C)和胸腺嘧啶 (T)四种。实验中常用聚脱氧腺苷酸（polydeoxyadenylic acid,简写为 poly(dA)）和聚脱氧胞苷酸（polydeoxycytidylic acid,简写为 poly(dC)）来模拟 DNA链。实验发现poly(dA)、poly(dC)和dAdC组成的嵌段高分子穿过α-HL孔的移位时间分布存在很明显的差别，20°C时poly(dA)100的平均移位时间约为poly(dC)100的7倍，结果归结为单元 dA和 dC与孔的相互作用不同[50,51]。进一步的模拟发现由链节A和C组成的嵌段高分子(AnCn)m的穿孔移位时间不仅与链节和孔的相互作用有关，还与嵌段AnCn的长度2n有关[32]。模拟中设链节A与孔的相互作用吸引强度εA不同于链节C与孔的相互作用吸引强度εC。

对于简单的AnCn两嵌段高分子，它有两种进入小孔的方式，即链节A先进入的方向A（Orientation A）和链节 C先进入的方向 C（Orientation C）。这两种进入方式的概率与εA和εC的大小有关。某一种链节与孔的相互吸引越强烈，那么相对应的进入方式出现的概率也越大。采用Rosenbluth-Rosenbluth方法计算得到的AnCn两嵌段高分子穿孔的自由能形貌见图7[52]。AnCn两嵌段高分子穿孔的自由能形貌与穿孔的方向和εA、εC的大小有关，同时移位时间也与穿孔的方向有关。依赖于εA与εC的大小，自由能形貌可能同时存在势垒和势阱。与单个势垒或势阱的情形不同，此时高分子的移位时间不仅与势垒和势阱的大小有关，也与势垒和势阱的位置有关。当链节A与孔吸引而链节C与孔排斥（εA=−1和εC=0）时，如图7(a)，高分子不同穿孔方向有不同的自由能形貌：方向 A先是小的势阱然后是一个很大的势垒，而方向C先是大的势垒然后是一个小势阱。对于方向C，只要高动能的高分子才能跨过大势垒，然后的小势阱只能有限地延长高分子的移位时间；而对于方向 A，前面的小势阱俘获了低动能的高分子，等高分子在热运动的帮助下积累了能量再通过后面的大势垒，这使得高分子的平均移位时间增大。因此我们发现高分子按方向A的移位时间要大于方向C的移位时间。而当链节A和C均与孔有较强的吸引（εA=−1和εC=−1.5）时，如图 7(b)，高分子两个穿孔方向都是势阱且势阱深度差不多，这使得高分子两个方向的移位时间差别不大。Monte Carlo模拟的时候把两个方向的移位时间分别统计平均值，模拟结果与自由能分析结果一致，见图8。为了加快高分子的穿孔速度，模拟时对在孔中的链节施加了f=0.5的驱动力。驱动力使自由能形貌倾斜，降低势垒的高度，这样使模拟时间缩短，但不影响前面的分析结果。

为了进一步验证从自由能角度出发进行分析的正确性，模拟过程中我们还记录了在εA=−1、εC=0.5时嵌段高分子的每个链节在孔中的滞留时间(waiting time)τw，结果如图9所示。因为链节A与小孔是相互吸引的，而链节C是排斥的，因此链节A相对来说更难离开小孔，其滞留时间普遍比链节C长。根据自由能形貌的分析，在εA=−1、εC=0.5时，当嵌段高分子A40C40以方向A进入小孔，会先遇到势阱，然后因为在x=40时会遇到很高的势垒，链节C很难进入小孔。这正符合了图9中方向A第20个链节到第40个链节的滞留时间特别长的现象。而以方向C进入小孔时，势垒出现在嵌段高分子刚进入小孔时，从图9可以看到，这时每个链节的滞留时间并不大，这进一步证明了之前的结论：高分子链刚进入小孔时碰到的自由能势垒并不会影响其移位时间。但这个势垒使方向C的穿孔概率大幅减小。我们发现当εA＜εC时，虽然τA＞τC,但方向 A的穿孔概率大于方向 C的穿孔概率。

图7.嵌段高分子A40C40以两种方向进入小孔的自由能形貌。(a) εA= −1，εC=0；和 (b)εA= −1，εC= −1.5。驱动力f=0。

图8.在εA=−1时，嵌段高分子A40C40以方向A进入小孔的移位时间τA和以方向C进入小孔的移位时间τC随εC的变化曲线。驱动力f=0.5。插图是两嵌段高分子链穿过小孔的不同穿孔方向的示意图。

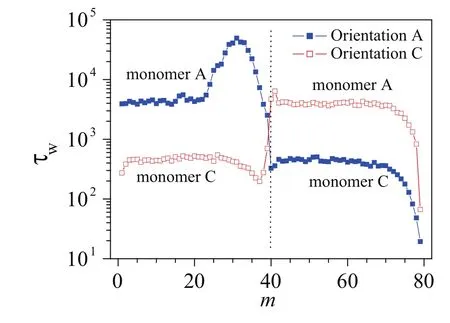
图9.嵌段高分子以两种方式通过小孔时每个链节在孔中的滞留时间的分布。这里嵌段高分子为A40C40，相互作用εA=−1和εC=0.5，驱动力 f=0.5。图中虚线表示两种A、C两种链节的交界处。

C.部分带电高分子穿孔

DNA穿孔的实验中，由于孔的直径小，外电场几乎都集中在孔中，电场驱动带电链节使链在孔中向前运动。为了更好的理解电场驱动力的作用，只考虑一个带电链节的高分子链模型，研究单个电荷受力对高分子链移位的影响。用Monte Carlo模拟和双吸收边界条件的Fokker-Planck方程（公式(8)）研究了单电荷高分子链穿孔的移位时间与电荷位置的关系[30,53]。图10给出了双吸收边界条件的Fokker-Planck方程计算得到的高分子链穿孔的移位时间与带电链节位置的关系曲线[53]，计算中初始穿过孔的链长m0取1，并假定高分子的扩散系数D是与带电链节位置无关的常数。理论的计算结果与Monte Carlo模拟结果高度一致[30]，反映了双吸收边界条件的Fokker-Planck方程确实能很好地计算高分子的移位时间。而采用反射吸收边界条件的Fokker-Planck方程（公式(7)）得到的计算结果[54]与Monte Carlo模拟结果不符[30]。

我们把中性不带电高分子（无驱动力）的移位时间记为τ0。图 10表明，当M/N＜0.5时，τ＞τ0，且τ先增大后减小；而当M/N＞0.5时，τ＜τ0，且τ先减小后增大。特别有趣的现象是，驱动力f越大，τ在M/N＜0.5区间的增加就越明显。

图10对应的自由能形貌见图11。由于带电链节通过小孔前后有一个−fL=−f（孔的长度L=1）的自由能下降，因此在M/N＜0.5时，带电链节的自由能下降和熵势垒的共同作用出现了一个自由能势阱，使移位时间大幅增加，而在M/N＞0.5时，不会出现这一势阱，因此高分子链可以较快地通过小孔。驱动力

越大，势阱越深，因此移位时间也越大。移位时间随驱动力增大而增加的现象可以用生活中的拔河来比喻，见图10的插图，驱动力f在拔河阶段与熵效应平衡。驱动力越大，高分子由于热运动而退出小孔的可能性就越小，因此平衡时间越久。进一步研究还发现，高分子的单个带电链节的位置不影响其标度理论，τ∼Nα，对两种边界条件及不同驱动力，α基本都保持2.35不变。

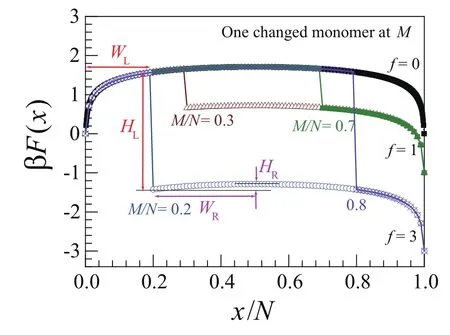
图11.不同驱动力f的情况下，单个电荷的高分子链穿孔自由能F(x)随带电链节位置M 的变化曲线。x是穿孔链节的数目。

D.高分子通过复合管道

两嵌段高分子链（ANACNC）在外界驱动下通过复合管道的输运过程对应的模型系统见图12的插图。复合管道由α和β两部分组成，管道宽度为2，仅能容下一个链节，因此高分子链顺序通过管道。高分子与管道的相互作用采用了Morse相互作用[55]

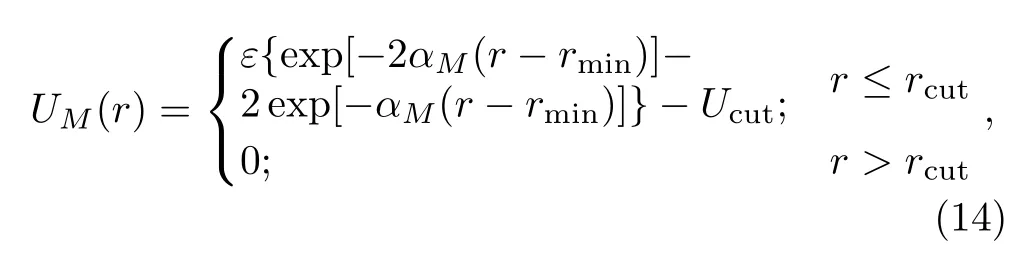
其中αM=24,rmin=0.8。A链段与管道α部分的相互作用参数为rcut=1和ε=εAα=3，而其余的相互作用参数取rcut=0.8和ε=1。因此复合管道与高分子A、C链段的相互作用除管道α部分与A链段之间存在强吸引作用之外，其它相互作用都为纯排斥作用。在此相互作用下，A链段先进入管道的概率远比C链段先进入管道的概率大。因此，我们只考察A链段先进入管道的移位过程。Monte Carlo模拟发现高分子链的移位时间与管道α部分的长度Lα有关，结果见图12[22]。

模拟结果表明：高分子链的输运过程显著依赖于管道α部分的长度，输运时间随管道α部分的长度的变化存在两个峰值。第一个峰的出现源于在 A链段全部进入管道之前高分子链会在第一个峰的位置遇到一个最深的自由能阱；而第二个峰的出现源于高分子A链段长度与管道α部分长度的相互匹配。因此第二个峰对应的管道α部分长度Lα与高分子A链段长度NA之间有简单的关系

其中bx是高分子键长沿管道方向的投影的平均长度。另外，模拟结果还表明利用复合管道可以有效调控嵌段高分子链的输运速度，这意味着复合管道可能在高分子序列检测中有潜在的应用。

E.温度对高分子移位的影响

由于高分子链的构象和扩散等性质都与系统温度有关，因此系统温度对高分子移位时间的影响比较复杂。实验仅观察到移位时间随温度的升高而下降[51,56−57]，而且观察到不同的下降方式，如幂律下降[57]和指数式下降[58]。计算机模拟发现移位时间在低温时随温度升高幂律下降，但在高温时则随温度的升高而增加[59]。

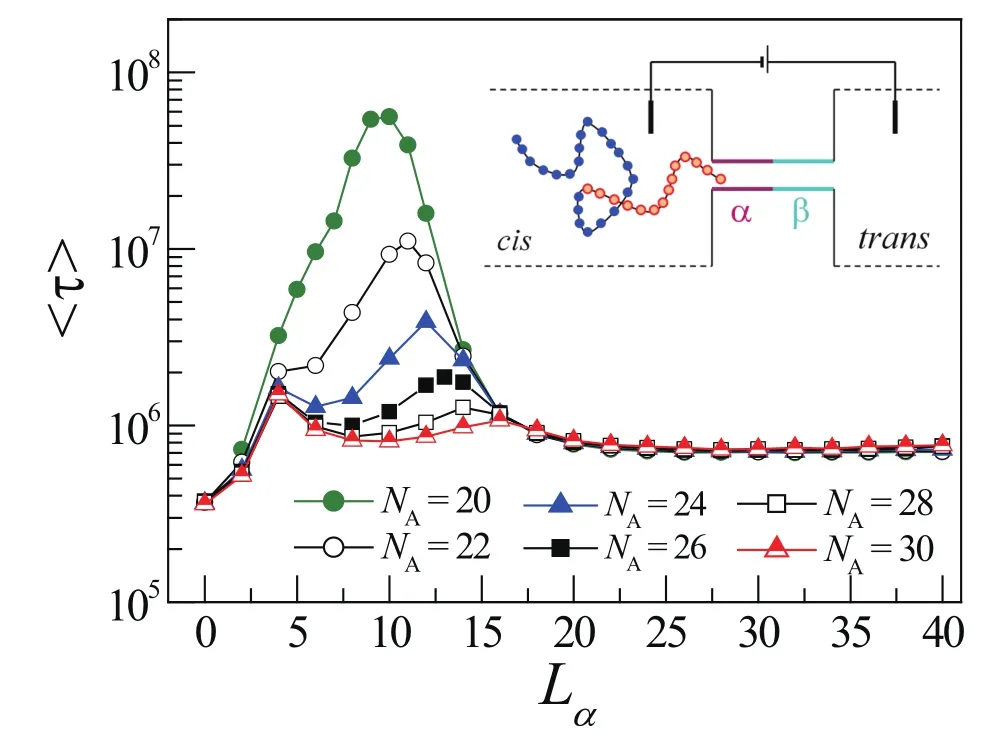
图12.不同 NA的高分子链的移位时间＜τ＞随 Lα的变化，模拟参数为：链长N=64，驱动力f=0.2，相互作用参数εAα=3。插图是两嵌段高分子链穿过复合管道的示意图。

我们利用Langevin动力学方法模拟了高分子链在不同温度通过小孔的移位过程[60]。为便于分析温度的影响，我们设定孔与高分子链为排斥作用，因此孔的性质与温度无关。与温度有关的量主要是高分子链的构象和高分子链的扩散系数。高分子链构象在低温是紧缩的液滴态，在塌缩相变温度以上转变为扩展的无规线团状。高分子链的扩散系数随温度的升高而线性增加。为了减少模拟时间，模拟中考虑了高分子链的链节在孔中受到一个驱动力f。高分子链的平均移位时间随温度变化的模拟结果见图13。

图13.高分子链的平均移位时间＜τ＞随温度T的变化，模拟参数为：链长N=128，驱动力f=0.5和1。插图给出了低温紧缩态和高温扩展态的示意图。

移位时间在低温下很大，这主要是由于低温下高分子处于紧缩构象的原因，这种情况下高分子的穿孔伴随着链节从紧缩构象上的剥离。随着温度的升高，高分子的构象变松，同时扩散系数增大，因此移位时间快速下降。随着温度的进一步升高，高分子的构象转变为高温的扩展态，此时构象熵S随温度的升高而变大，自由能势垒也随构象熵S的增大而增大，这将使移位时间增加，但同时扩散系数的增大又降低了高分子的移位时间。我们发现，移位时间在塌缩相变温度附近最小。在塌缩相变温度以上，移位时间随温度的升高而增大。移位时间在高温的升高源于高分子尺寸的增大和驱动力的高温软化。理论指出高分子的移位时间应与高分子扩散自身回转半径RG的时间相当[61]，即τ∼R2G/D，因此高分子尺寸的增加导致高分子移位时间的上升。另一方面，驱动力f拉动高分子通过小孔，前进一步长度 Δx和退后一步长度Δx的概率分别为

因为P+随温度的升高而下降，因此驱动力的作用随着温度的上升而下降，表现为驱动力的高温软化。

可见，温度对高分子移位的影响至少来源于5个因素：（1）扩散系数随温度的升高而增加；（2）高分子的构象熵随温度升高而增加；（3）驱动力随温度升高而软化；（4）高分子尺寸随温度升高而增大；（5）低温高分子处于低能量的紧缩态，温度的升高导致结构变松，能量升高。因素（1）、（2）和（5）导致移位时间随温度的升高而下降，而因素（3）和（4）导致移位时间随温度的升高而增加，从而产生高分子移位时间复杂的温度依赖性[60]。

V.结论

高分子链通过纳米孔的移位时间主要受自由能形貌的影响，理论计算和模拟研究表明可以通过改变链与管道的相互作用、链的组分、链节电荷分布、管道的性质、温度等因素来调控自由能形貌和移位时间。未来的主要研究方向是如何调控高分子链的运动，希望通过人工设计的纳米管道实现高分子运动的调控，达到分离、检测不同高分子、DNA、蛋白质的目的。

致谢

本工作得到国家自然科学基金（11374255,11674277）资助。

参考文献

[1]Han J,Craighead H G.Science,2000,288:1026

[2]Venkatesan B M,Bashir R.Nature Nanotech.,2011,6:615

[3]Milchev A.J.Phys.:Condens.Matter,2011,23:103101

[4]Palyulin V V,Ala-Nissila T,Metzler R.Soft Matter,2014,10:9016

[5]Miles B N,Ivanov A P,Wilson K A,Do˘gan F,Japrung D,Edel J B.Chem.Soc.,Rev.2013,42:15

[6]Muthukumar M,Plesa C,Dekker C.Phys.Today,2015,68:40

[7]Kasianowicz J J,Brandin E,Branton D,Deamer D W.Proc.Natl.Acad.Sci.USA,1996,93:13770

[8]Robertson J W F,Rodrigues C G,Stanford V M,Rubinson K A,Krasilnikov O V,Kasianowicz J J.Proc.Natl.Acad.Sci.USA,2007,104:8207

[9]Kowalczyk S W,Hall A R,Dekker C.Nano Lett.,2010,10:324

[10]Clarke J,Wu H C,Jayasinghe L,Patel A,Reid S,Bayley H.Nature Nanotech.,2009,4:265

[11]Zhang Z S,Shen J W,Wang H B,Wang Q,Zhang J Q,Liang L J,˚Agren H,Tu Y Q.J.Phys.Chem.Lett.,2014,5:1602

[12]Liu L,Yang C,Zhao K,Li J Y,Wu H C.Nature Commun.,2013,4:2989

[13]Zhang S,Wang X F,Li T,Liu L,Wu H C,Luo M B,Li J Y.Langmuir,2015,31:10094

[14]Wei R,Gatterdam V,Wieneke R,Tampe R,Rant U.Nature Nanotech.,2012,7:257

[15]Healy K,Schiedt B,Morrison A P.Nanomedicine,2007,2:875

[16]Liang L J,Wang Q,˚Agren H,Tu Y Q.Frontiers Chem.,2014,2:5

[17]Luan B,Stolovitzky G,Martyna G.Nanoscale,2012,4:1068

[18]Ying Y L,Zhang J J,Gao R,Long Y T.Angew.Chem.Int.Ed.,2013,52:13154

[19]Cao C,Ying Y L,Hu Z L,Liao D F,Tian H,Long Y T.Nature Nanotechnol.,2016,11:713

[20]Sun L Z,Cao W P,Luo M B.J.Chem.Phys.,2009,131:194904

[21]Luo M B,Cao W P.Phys.Rev.E,2012,86:031914

[22]Wang C,Chen Y C,Zhang S,Luo M B.Macromolecules,2014,47:7215

[23]Katkar H H,Muthukumar M.J.Chem.Phys.,2014,140:135102

[24]Zhang S,Wang C,Sun L Z,Li C Y,Luo M B.J.Chem.Phys.,2013,139:044902

[25]Sung W,Park P J.Phys.Rev.Lett.,1996,77:783

[26]Muthukumar M.J.Chem.Phys.,1999,111:10371

[27]Muthukumar M.J.Chem.Phys.,2003,118:5174

[28]Luo M B.Polymer,2007,48:7679

[29]Chuang J,Kantor Y,Kardar M.Phys.Rev.E,2001,65:011802

[30]Qian H,Sun L Z,Luo M B.J.Chem.Phys.,2012,137:034903

[31]Muthukumar M.Phys.Rev.Lett.,2001,86:3188

[32]Luo K F,Ala-Nissila T,Ying S C,Bhattacharya A.Phys.Rev.Lett.,2008,100:058101

[33]de Haan H W,Slater G W.Phys.Rev.Lett.,2013,110:048101

[34]Sarabadani J,Ikonen T,Ala-Nissila T.J.Chem.Phys.,2015,143:074905

[35]Lam P M,Zhen Y.J.Stat.Phys.,2015,161:197

[36]Symeonidis V,Karniadakis G E,Caswell B.Phys.Rev.Lett.,2005,95:076001

[37]Metropolis N,Rosenbluth A W,Rosenbluth W N,Teller A H,Teller A.J.Chem.Phys.,1953,21:1087

[38]Groot R D,Warren P B.J.Chem.Phys.,1997,107:4423

[39]Mirigian S,Wang Y B,Muthukumar M.J.Chem.Phys.,2012,137:064904.

[40]Barber M N,Guttmann A J,Middlemiss K M,Torrie G M,Whittington S G.J.Phys.A,1978,11:1833

[41]Rosenbluth M N,Rosenbluth A W.J.Chem.Phys.,1954,22:881.

[42]Grassberger P.Phys.Rev.E,1997,56:3682

[43]Polson J M,McCaあrey A C M.J.Chem.Phys.,2013,138:174902

[44]Luo K F,Ala-Nissila T,Ying S C,Bhattacharya A.Phys.Rev.Lett.,2007,99:148102

[45]Gopinathan A,Kim Y W.Phys.Rev.Lett.,2007,99:228106

[46]Yang S,Neimark A V.J.Chem.Phys.,2012,136:214901

[47]Cao W P,Sun L Z,Wang C,Luo M B.J.Chem.Phys.,2011,135:174901

[48]Yu W C,Luo K F.J.Am.Chem.Soc.,2011,133:13565

[49]Cao W P,Ren Q B,Luo M B.Phys.Rev.E,2015,92:012603

[50]Meller A,Nivon L,Brandin E,Golovchenko J,Branton D.Proc.Natl.Acad.Sci.U.S.A.,2000,97:1079

[51]Meller A,Branton D.Electrophoresis,2002,23:2583

[52]Sun L Z,Cao W P,Luo M B.Phys.Chem.Chem.Phys.,2010,12:13318

[53]Wu F,Yang X,Luo M B.J.Polym.Sci.B-Polym.Phys.,2017,55:1017

[54]Mohan A,Kolomeisky A B,Pasquali M.J.Chem.Phys.,2008,128:125104

[55]Milchev A,Klushin L,Skvortsov A,Binder K.Macromolecules,2010,43:6877

[56]Verschueren D V,Jonsson M P,Dekker C.Nanotechnology2015,26:234004

[57]Payet L,Martinho M,Merstorf C,Pastoriza-Gallego M,Pelta J,ViasnoあV,Auvray L,Muthukumar M,Math´e J.Biophys.J.,2015,109:1600

[58]Matysiak S,Montesi A,Pasquali M,Kolomeisky A B,Clementi C.Phys.Rev.Lett.,2006,96:118103

[59]Loebl H C,Randel R,Goodwin S P,Matthai C C.Phys.Rev.E,2003,67:041913

[60]Luo M B,Tsehay D A,Sun L Z.J.Chem.Phys.,2017,147:034901

[61]Carson S,Wanunu M.Nanotechnology,2015,26:074004

Theoretical and simulational studies on the dynamics of polymer translocation

Wu Fan,Luo Meng-Bo
Department of Physics,Zhejiang University,Hangzhou 310027

The translocation of polymer chains through nanotubes or nanopores is an important phenomenon which is highly concerned in physics,chemistry,and biology.It is of potential applications in life process and technology fi eld,and extensive experimental,theoretical,and simulation investigations on this phenomenon have been carried out.This review article summarizes the latest theoretical and simulation progress on the polymer translocation,and discusses the dynamic process of polymer chain translocation in the framework of translocation time.Based on the theoretical calculations and simulations,the dependence of free energy landscape on the polymer-pore interaction,composition and charge distribution of polymer chain,details of nanopores,and temperature are discussed and compared with the predictions of free energy landscape.The results are helpful for a better understanding of the underlying mechanisms and controlling approaches of polymer translocation.

Polymer chain;Nanopore;Nanotube;Translocation;Computer simulation

O631.12

10.13725/j.cnki.pip.2017.06.002

1000-0542(2017)06-0212-13

*E-mail:luomengbo@zju.edu.cn

date:2017-8-2