例谈基于问题解决的高中数学复习

王 坤

(北京市第八十中学 100102)

对于很多数学知识的学习，不单单是记住一个概念和表述一个知识，而是将知识与方法应用于具体的问题，在问题解决的过程中掌握该知识与方法．

探究学习是基于问题解决的一种学习方式，在高中数学知识的初学阶段，由于学习时间比较充裕，学生可以针对当天所讲内容进行探究学习，这种探究是一种专项探究，思维容量一般不大．而进入高中数学知识的复习阶段，囿于时间的限制，教师一般采用组织多轮复习的方式，反复强化已有知识，对数学思维能力的培养与提升关注更加的少．

那么如何在复习阶段继续通过探究，既复习知识，又提升思维能力呢？笔者通过多年的教学实践，认为可以通过设计有价值的问题，串接许多相关的知识，建立不同知识之间的内在联系，织就庞大的知识网络．

下面就通过一系列问题的解决，设计一节高三复习课(两课时)．

【学生活动】自主探究最小距离．

【预设错解】部分学生经验使然，直接将函数的单调性、均值不等式等知识机械迁移，认为点(1,2)和(-1，-2)到距离原点O的距离最小值．

【教师点评】知识的迁移需要注意具体的条件，机械的迁移往往产生错误的结论，知识的迁移可以形成猜想，猜想是需要经过证明或者检验的．问题的解决方法的选择需要基于目标问题的形式及其与条件的关系来确定，在本题中，最终的目标涉及两点距离，而过程目标又涉及均值不等式．

【学生活动】学生初步分析，认识问题，从不同角度尝试组织探究思路．

【学生活动】学生作图时，能够注意以下几点：

【猜想1验证】(以第二种表述为例)

【教师点评】学习的过程是知识巩固与扩充的过程，在学习的过程中，除了巩固具体的知识，还要熟练解决问题的方法，同时充分调动对比、类比、归纳、联想等思维方式，尽量扩大知识成果的范围，形成越来越大的知识体系格局．

【学生活动】结合图形，学生继续探究．

【解法指导】证明图形(或图象)的对称性的方法如下：

图形(或图象)上的任意点关于直线(或点)的对称点依然在该图形(或图象)上．

【教师点评】在几何猜想的形成过程中，应熟练使用几何图形全等、相似、位似、对称等关系与性质的表述，熟练使用平移、伸缩等变换．在图象的性质证明方面，广泛采用坐标分析法，即从图象上任意点的坐标入手进行，结合对称、周期等性质的代数特征，进行证明．

【教师点评】通过本问题的解决，我们明确这样的结论：

(1)如果一个图形C关于点M中心对称，同时关于直线l轴对称，且直线l经过点M，那么经过点M的直线l的垂线l′也是图形C的对称轴；

(2)如果一个图形C同时关于两条互相垂直的直线l,l′轴对称，那么图形C关于直线l,l′的交点M中心对称．

问题5通过上述问题，以及一系列猜想，你还想到了什么？

对于猜想4，不再进行证明，而采用几何画板直观验证．

【学生活动】结合两个提示，选择恰当的方法与角度，进行知识迁移，形成猜想．

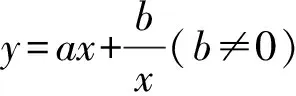
【解法指导】对于猜想5，两个定点通过什么方法来寻找是证明的关键．

类比双曲线的几何性质，形成下面的研究思路：

最后，用“离心率”乘以“顶点”坐标，得到“焦点”坐标，即两定点坐标；两“顶点”距离即为定值．

【猜想5证明】当a>0,b>0时，推导过程如下：

根据基本不等式，|OP|最小值为

由此可得“双曲线”的离心率

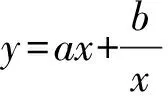
当a∈R,b≠0的其它情形，结论类似，在此不再赘述．

【提示2证明】

【猜想6证明】

因此P为线段AB的中点．

知识的类比迁移，可以在不同知识模块间互通有无，极大地拓宽知识网络边界，在新结论“创新”过程中，大家可以体会数学知识“变与不变”的辩证统一性．

通过上述教学案例的设计，我们可以发现，高中总复习阶段，虽然是复习，但并不意味着知识学习的原地踏步，在对基础知识和方法有了初步认识之后，通过问题解决的方式，调动各种策略性知识的应用，可以帮助学生在应用中体会相关知识的作用与联系．如果一味地停留在单独某一模块知识上的机械重复，只能僵化学生思维，无益于学生数学能力的提高．