CT图像重建中基于指数形式的滤波函数优化
2017-12-25益海
, ,,益海,,,
(兰州大学 核科学与技术学院,兰州 730000)
CT图像重建中基于指数形式的滤波函数优化
马思汉,张催,陈章谷,张益海,潘小东,商宏杰,李公平
(兰州大学 核科学与技术学院,兰州 730000)
计算机断层成像(CT)技术广泛应用于工业、医疗、国防、航空航天等领域。随着科学技术的不断发展,对使用CT来获得更加精确的材料内部结构信息提出了更高的要求,希望能在重建图像中更加完整地表达组织结构信息。为了获取更好的图像质量,提出一种基于指数形式的滤波函数(EBFF),在MATLAB平台下采用EBFF对图像进行重建,并通过相似系数、归一化平均值以及归一化均方根距离等评价手段与几种传统的滤波函数重建图像结果进行对比,同时在锥束CT实验平台下采用EBFF进行图像重建。模拟与试验均表明EBFF对重建图像质量有一定改善,其较传统滤波函数能给出更好的重建结果,有助于图像重建结果的优化。
图像重建;滤波反投影算法;滤波函数;Radon变换
X射线CT检测法具有空间和密度分辨率高、扫描速度快、成像时间短以及强穿透力等特点,可以获取与工件材料结构、成分以及密度等特性相关的二维断层图,并生成三维立体图像[1],因此作为一种无损检测的重要手段,被广泛应用于多个领域。要得到高质量的CT图像,除硬件条件外,图像重建方法也扮演着重要角色。CT图像重建方法主要分为两类:解析法和迭代法。其中迭代法包括代数重建法(ART)、最大期望算法(EM)等,解析法包括傅里叶变换重建算法、滤波反投影重建算法(Filtered Back Projection, FBP)和反投影滤波重建算法等[2]。迭代算法适用于投影数据不足、投影角缺失以及投影间隔不均匀的场合,但其迭代次数较多,计算强度较高,需要较长的时间,在工业和临床医疗等方面的应用具有较大的局限,一般情况下较少采用。
最常用的一种图像重建算法是解析法中的FBP算法[13],虽然该方法要求具有完整的投影数据,抗噪能力相对较弱,但其能够处理庞大的数据,具有极快的重建速度,所以,该算法在实际应用中最为常见。而在FBP算法中,滤波函数的选取尤为重要,其决定了重建图像质量的好坏,采用不同的滤波函数重建图像可以达到不同的效果。目前,滤波函数的优化仍然是进一步提高CT图像质量的途径之一。传统滤波函数包括Hann、Ram-Lak以及基于其特性改进的滤波函数。笔者从FBP原理出发提出一种基于指数形式的优化滤波函数(EBFF),并对优化函数及传统滤波函数的重建图像质量进行定量地比较,讨论优化滤波函数的滤波特性,并就其对重建图像质量的影响做出评价。
1 滤波反投影重建基础
1.1 Radon变换
在图像重建过程中,Radon变换是一种基于基本数学理论建立的图像投影变换方法,Radon变换表明某一物体可用多个投影数据来表示,对于穿过物体的一条直线,该投影数据表示沿直线所在路径的线积分,其原理如图1所示。已知二维分布函数f(x,y)及二维平面内一条直线L,原点到直线L的距离为t,与x轴夹角为α,沿直线的L投影数据为q,坐标(x,y)可用极坐标(r,φ)表示为:
那么投影数据用极坐标可表示为:
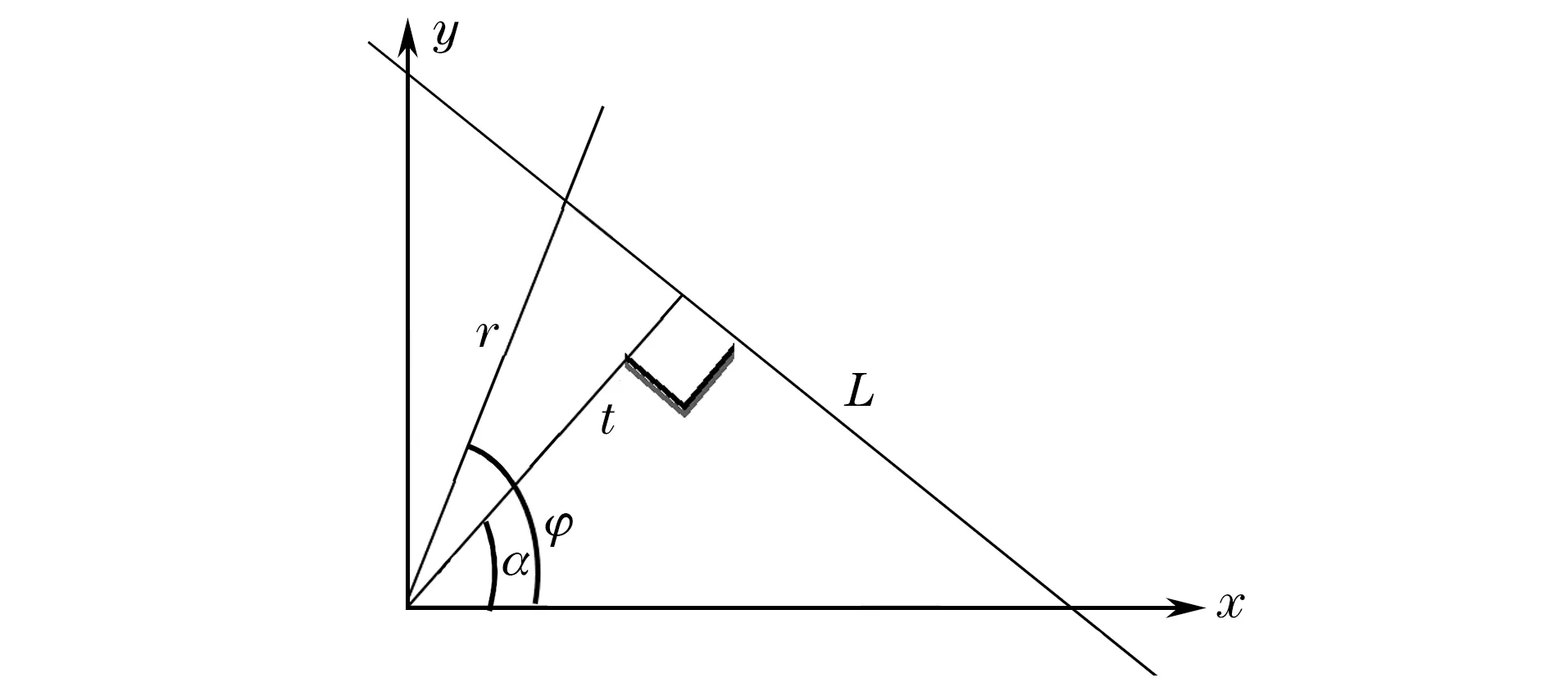
图1 Radon变换原理示意
1.2 滤波反投影重建原理
以Radon变换为基础进行数据投影,设原始图像数据为f(x,y),δ(x)是一种广义函数,定义投影图像数据为
式中:θ为投影角度。
当s=xcosθ+ysinθ时,δ(xcosθ+ysinθ-s)=1,其他情况δ(xcosθ+ysinθ-s)=0。那么在投影角度θ下的投影图像数据qθ(s)表示为:

对式(4)进行Fourier变换,获得变换后的投影数据Gθ(ω)表示为:

对式(5)加入滤波函数H(ω)进行Fourier逆变换得到滤波修正处理后的数据Pθ(s):

再对数据Pθ(s)进行反投影变换处理获得重建图像。
2 滤波函数及其特性
2.1 常用滤波函数
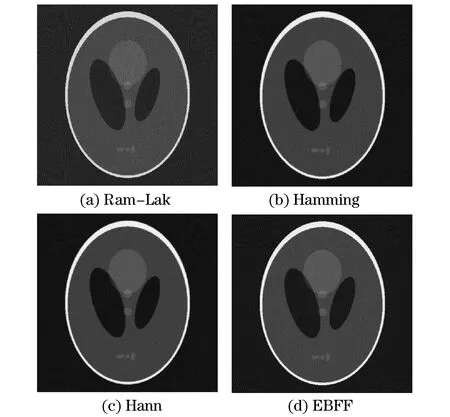
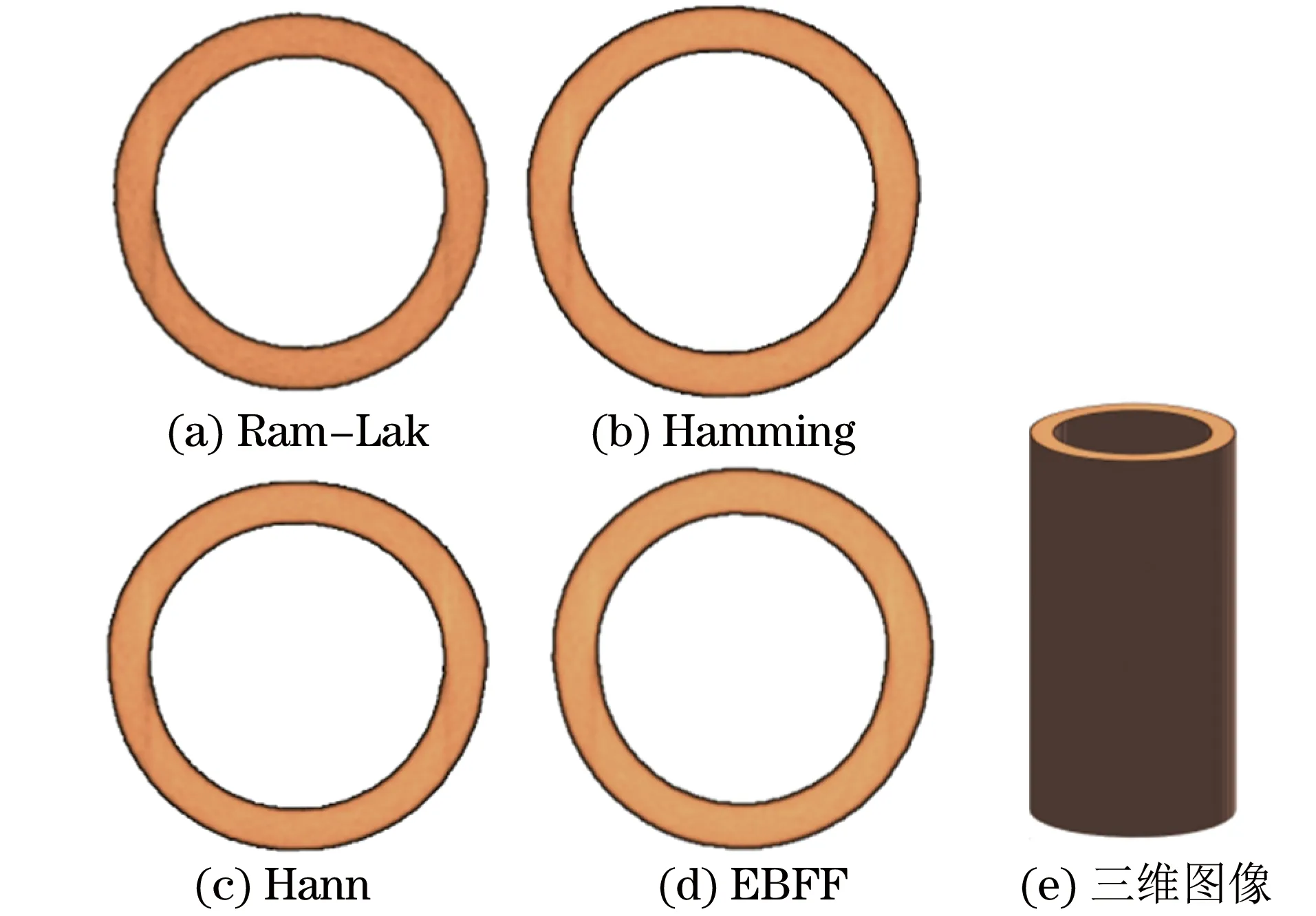
经典滤波从功能上主要分为高通滤波、低通滤波和带通滤波,其每一种又可以分为模拟滤波和数字滤波,图像处理要求使用不同频域范围内的数字滤波,而对于不同的实际情况会选择不同的滤波函数。滤波函数的幅频特性是图像重建误差的决定性因素,表征幅频特性的指标又分为主瓣特性和旁瓣特性。对于一个良好的滤波函数,一般要求具有良好的幅频特性,也就是说在选取滤波函数时,要遵循一定原则:主瓣幅值高宽度窄,以获得较陡的过渡带;第一旁瓣相对主瓣幅值尽可能小,以改善平稳度和增大阻带衰减。在滤波反投影算法中有诸多的滤波函数可以使用,例如,H(ω)=|ω|rect(ω/2R)表示理想滤波函数,其中|ω|为理想滤波函数频率,R为实际图像频率的上限。rect为矩形函数,当|ω| 对EBFF函数中的C取不同的值,得到C取6时,效果较好,分析其滤波函数特性,并与其他滤波函数重建图像比较。不同滤波函数的频域特性曲线如图2所示。 表1 不同滤波函数的表达形式 图2 不同滤波函数的频域曲线 基于一定的数学理论基础,对一定频域内的滤波函数进行Fourier变换以及级数展开分析其幅频特性,评价滤波效果。已知H(ω)是偶函数,将其Fourier变换到空域滤波时,函数h(S)也为偶函数,其表现形式如式(7)所示。 h(S)可以根据级数展开,得到以下展开式: 式(8)进一步变换可得到: 式中:m0为主瓣幅值。 令h(S)=0,则 m0-m2(2πS)2/2+m4(2πS)4/24-…=0 得到方程的解Sk(代表k次幂的第k个解),根据展开式以及方程的解讨论滤波函数的特性。式(10)中主瓣幅值为m0,宽度为d0=2S0,旁瓣幅值为h(Sk+dk/2),宽度为dk=Sk+1-Sk,表2给出R=0.5时的几种滤波函数在空域下的主瓣与第一旁瓣的幅值与宽度参数[6]。 对于滤波图像的空间分辨率,要求滤波函数主瓣幅值越高宽度越窄,主瓣尽可能地窄,以获得较陡的过渡带,从而获得较高的空间分辨率。而对于图像密度分辨率,要求其旁瓣幅值和宽度尽可能小,以得到较高的密度分辨率。尽量减少滤波函数主瓣和旁瓣的相对幅度,也就是使信号尽量集中于主瓣,减小峰肩和纹波,进行增加阻带的衰减。空间分辨率是指能分辨最小物体的能力,密度分辨率指能分辨图像的最小密度差,在投影数据一定的情况,空间分辨率和密度分辨率互相矛盾。对比表2的数据可以看出,Ram-Lak滤波函数的主瓣幅值最大,宽度最窄,说明图像的空间分辨率最好,但是其旁瓣幅值较大宽度较宽,密度分辨率较差。Hann和Hamming滤波函数的主瓣幅值较小,主瓣宽度较宽,第一旁瓣幅值较小,但旁瓣宽度最大。对于EBFF,主瓣宽度相比Hann与Hamming函数较窄,而较Ram-Lak函数较宽,主瓣幅值较Ram-Lak函数小,比Hann与Hamming函数大,对于旁瓣幅值而言Ram-Lak最大,EBFF幅值最小,并且旁瓣宽度最小,说明其密度分辨率最好,综上所述,EBFF能在空间和密度分辨率中取得较好的折中。 表2不同滤波函数主瓣和第一旁瓣的幅值和宽度 滤波函数主瓣幅值主瓣宽度第一旁瓣幅值第一旁瓣宽度Ram-LakHannHammingEBFF0.25090.08840.07430.21061.55942.05772.29081.6676-0.0823-0.0272-0.0227-0.01770.32300.75850.88680.2765 模拟试验采用经典Shepp-logan头部模型[8],重建图像像素尺寸为512个×512个,对图像用平行束进行投影生成投影图像,取180个投影角,每一次投影的增加角度为1°,采用Ram-Lak、Hann、Hamming滤波函数以及优化后的EBFF对Shepp-logan模型进行全局重建,分析不同函数的滤波重建效果。重建结果如图3所示。 图3 不同滤波函数的重建图像(MATLAB模拟) 对比图3中不同滤波函数的重建效果,可以看出直接反投影图像模糊,边界不清,滤波反投影后图像效果较好,但Ram-Lak滤波图像比较粗糙,图像伪影较多,视觉舒适度较差,而Hamming滤波、Hann滤波和EBFF重建图像较光滑,伪影较少。而相比EBFF重建图像要好,Hann滤波边界伪影较多,EBFF图像伪影相对较少。 对比滤波图像,取不同滤波函数重建图像的第250行灰度数据进行比较,分析滤波后灰度值的波动情况,结果如图4所示。 图4 几种滤波函数重建图像与原始图像的灰度数据(第250行)对比 从图4可看出,Ram-Lak滤波函数波动较大,原因在于其对频域内的各个频域部分进行了线性放大,在放大高频分量时,也放大了高频噪声,产生严重的Gibbs现象。EBFF能较好地减小Gibbs效应的影响,对各个频域分量进行非线性放大的同时,较好地减小了高频噪声,弱化了噪声对重建图像质量的影响,故重建图像的质量较好[7]。 不同滤波函数的滤波效果会有所不同,重建图像的质量也会有所差异。为量化比较上述滤波函数对图像重建质量的影响,分别将上述4幅图像与原始图像对比,计算其相似系数ε,归一化均方根距离d以及归一化平均值r,信噪比SNR。 表3 不同滤波函数的评价数据比较 ε表示滤波图像与原始图像的相似程度,值越大,滤波效果越好,空间分辨率越高;d较为灵敏地反映了少数点、大误差的情况[11];r反映了多数点、小误差的变化;与d相反,SNR反映信号值与噪声大小的比值,值越大,图像质量越好。 对比表3中的计算结果,Ram-Lak滤波函数的ε最大,说明与原始图像最接近,d以及r值都是最小,反映了误差变化小的特点,但是SNR值最小,说明噪声干扰较强。EBFF的d值相比Hann,Hamming的要小,三者滤波性能以及图像分辨率肉眼差异不大。表中可直观得出EBFF信噪比SNR比Ram-Lak的大,相比Ram-Lak滤波函数抗噪能力更佳。而EBFF的r值较Hann和Hamming的小,说明对于减小误差的多数点而言其图像效果更佳。 由于Ram-Lak函数与原始图像的灰度值相接近,即使波动较大,按照上述公式计算,ε仍然最大,但是得到的SNR最小,图像伪影较多,视觉效果较差。综合考虑,选取EBFF函数能得到一种折中的结果,获得较为良好的重建效果。 通常情况下,在滤波重建分析中要考虑噪声对重建图像的影响,一般情况下考虑泊松噪声的影响,因此,在模拟中对数据加入泊松噪声[12],得下式。 通过改变噪声参数λ来改变模拟噪声的大小,得到重建图像,分析不同噪声情况下的重建图像质量,获得评价数据,通过ε、d和r对重建图像质量进行评价。加入λ=2的泊松噪声重建图像如图5所示,评价数据如表4所示。 对比表3及表4,图5可看出,对于加入噪声后的图像质量,采用Ram-Lak函数后的评价值变化最大,其抗噪性能最差,其他滤波函数的评价值变化相对较缓。由表3可以看出,EBFF的d以及r都小于其他函数,其对应分辨率相比其他函数要好,加入噪声后,抗噪性能较好。而对于该滤波函数在实际中的应用效果,还需在试验中进一步验证。 图5 加入泊松噪声 (λ=2)后不同滤波函数的重建图像 滤波函数εdrRam-LakHannHammingEBFF0.91880.97250.97140.97150.42660.31820.32010.31460.54170.40970.40460.3965 试验采用外径1.5 cm的铝材圆柱管作为重建物体,重建图像像素尺寸为300个×300个,源距离探测器80.5 cm,源-物距离75 cm,探测器像素尺寸0.127 mm。对图像用小角度扇形束进行投影生成投影图像,取360个投影角,每一次投影的增加角度为1°,采用Ram-Lak,Hann,Hamming以及EBFF对重建物体全局进行重建,取重建图像某一断层切片进行分析,比较不同函数的重建效果。铝圆柱管的不同滤波函数的试验重建与MATLAB重建结果如图6,7所示,取各滤波函数的第150行灰度值图像进行分析,如图8所示。 图6 铝圆柱管的不同滤波函数的试验重建图像 图7 铝圆柱管的不同滤波函数的MATLAB图像重建及其三维图像 图8 各滤波函数重建图像的第150行灰度数据及其局部放大数据 对比图6中的断层重建结果,表明EBFF的重建效果相较其他3种滤波函数要好。图7为利用MATLAB模拟生成的可视化立体图像,可明显看出各种滤波函数重建图像能力的差别。对于图8标注部分而言,Ram-Lak灰度值波动最大,EBFF边缘拐点值与峰值差为0.073 9,Hamming函数重建图像灰度拐点值与峰值差为0.112 1,表明EBFF灰度值波动最小,优化获得的图像质量良好。综上所述,试验和模拟的结果吻合得较好,优化函数性能较好。 (1) Hann、Hamming以及EBFF都能很好地消去部分噪声,减少噪声的影响;相比传统滤波函数,EBFF具有更良好的图像重建效果,提高了图片的分辨率,重建图像质量更佳。 (2) EBFF具有较大的主瓣幅值,主瓣附近旁瓣幅值也较小,能使有用信号集中于主瓣,减小了对噪声的放大,能有效抑制噪声对图像的影响,表明EBFF在抗噪方面的性能较好。 (3) 就上述几种滤波函数而言,EBFF能得到相对较好的重建图像质量, 但其图像分辨率和抗噪性能还有待进一步提高,图像锐度还需改善。 [1] 董方旭, 王从科, 凡丽梅, 等. X射线检测技术在复合材料检测中的应用与发展[J].无损检测,2016,38(2): 67-72. [2] 张朝宗. 工业CT技术和原理[M]. 北京:科学出版社, 2009. [3] 谷雨, 胡以华, 郝士琦,等. 激光反射层析成像中滤波反投影算法特性研究[J]. 激光与红外, 2015(12):1500-1504. [4] SHEPP L A, LOGAN B F. The Fourier reconstruction of a head section[J]. IEEE Transactions on Nuclear Science,1974,21(3):21-43. [5] 蔚慧甜. 基于汉宁窗函数的滤波器的设计[J].传感器世界, 2011, 17(12):27-29. [6] 徐茂林, 邱钧, 范惠荣,等. 用一种新滤波函数作CT图像局部重建[J]. 计算物理, 2004, 21(3):362-368. [7] 张顺利, 李卫斌, 唐高峰. 滤波反投影图像重建算法研究[J]. 咸阳师范学院学报, 2008, 23(4):47-49. [8] 胡君杰, 马晨欣, 闫镔. CT图像重建中滤波函数的优化[J]. CT理论与应用研究, 2013, 22(1):85-92. [9] 张东平, 张定华, 张丰收,等. 滤波器对滤波反投影重建图像质量的影响[J].机械设计与制造,2007(9):66-68. [10] 张玉杰, 潘尚峰, 卢超. 工业 CT 旋转扫描台回转精度对成像质量的影响[J]. 无损检测, 2016, 38(10): 37-41. [11] 杨威,赵剡,许东.基于人眼视觉的结构相似度图像质量评价方法[J].北京航空航天大学学报,2008,34(1):1-4. [12] 骆岩红. CT图像重建滤波反投影算法中指数滤波器的研究[J]. 计算机科学, 2014, 41(Z1):220-223. [13] 张益海, 张催, 潘小东, 等. 锥束工业 CT 射束硬化校正方法[J]. 无损检测, 2017, 39(6): 8-12. OptimizationofExponential-BasedFilterFunctioninCTImageReconstruction MA Sihan, ZHANG Cui, CHEN Zhanggu, ZHANG Yihai , PAN Xiaodong,SHANG Hongjie, LI Gongping (School of Nuclear Science and Technology, Lanzhou University, Lanzhou 730000, China) Computed tomography (CT) has been widely applied in industrial, medical, defense, aerospace and other fields. With the continuous development of science and technology, higher requirements on CT for getting more accurate information on the internal structure of the material are put forward and one hopes to display more detailed and complete organizational structure information in reconstruction image. In this article, an exponential-based filter function(EBFF) is proposed to obtain a better image quality by using exponential-based filter function to reconstruct the image in the MATLAB platform, and the parameters ofε,randdare exploited to compare image reconstruction results with several traditional filter functions. Furthermore, EBFF was used to reconstruct the image under the experimental platform of cone beam CT. Both simulation and experiment results show that EBFF has some improvement on the reconstructed image quality, and compared to the traditional filter function EBFF can give a better reconstruction result and is helpful to the optimization of the results of image reconstruction. image reconstruction; FBP algorithm; filter function; Radon transformation TG115.28;TL99 A 1000-6656(2017)12-0001-06 2017-06-13 兰州大学创新创业教育基地建设资助项目 马思汉(1995-),男,硕士,主要从事X射线成像研究 李公平,ligp@lzu.edu.cn 10.11973/wsjc201712001

2.2 滤波函数主瓣与旁瓣特性


3 MATLAB试验模拟
3.1 理想环境下图像重建

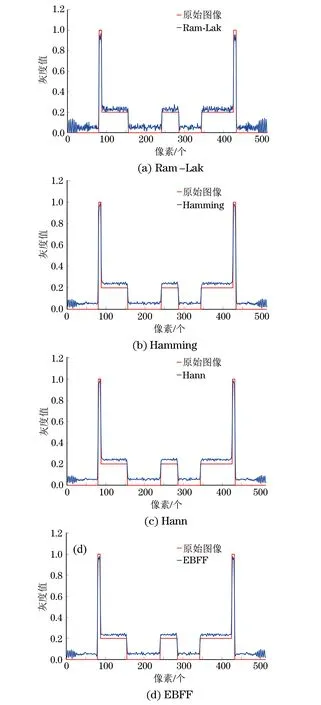


3.2 噪声环境对重建结果的影响


4 试验方法与应用


5 结论
