基于电化学模型的锂离子电池多尺度建模及其简化方法∗

庞辉

(西安理工大学机械与精密仪器工程学院,西安 710048)

基于电化学模型的锂离子电池多尺度建模及其简化方法∗

庞辉†

(西安理工大学机械与精密仪器工程学院,西安 710048)

电动汽车,锂离子电池,电化学,模型简化

1 引 言

锂离子电池由于具有轻量化、低放电率和高能量密度等诸多优点,在电动汽车中获得了广泛应用,其精确建模和参数估计在电池能量管理系统中起到至关重要的作用[1].因此,通过计算机数值仿真技术,建立锂电池数学物理模型,能够全面系统地描述电池充放电过程的电化学行为,分析其演化规律,为优化电池系统设计提供理论支撑[2].

目前,研究人员构建了涵盖锂离子电池能量传递、质量传递以及电荷传递的多维多物理场模型,如等效电路模型[3,4]、平均电化学模型[5−7]、单粒子模型[8−10]、准二维电化学模型[11−13],它们之间的计算复杂度和模型可预测性关系如图1所示.

鉴于锂离子电池实际使用工况的复杂性,人们对锂离子电池的内部应力和浓度分布、荷电状态、电池热耦合特性、容量衰减以及电极极化等方面开展了深入系统的研究.由Doyle和Newman[14]提出的锂电池准二维模型(pseudo-two-dimensions,P2D)广泛应用于描述锂离子电池电化学动力学行为,具有模型准确、计算精度高等优点.但是,严格的P2D模型包括复杂的耦合非线性偏微分方程,其计算求解复杂且效率较低.尽管人们提出了许多求解P2D模型的方法,如本征正交分解方法、Lyapunov-Schmidt方法、坐标转换和正交配置结合方法等[15−18].然而,由于计算成本较高,P2D模型难以直接应用于电动汽车的参数在线估计和实时控制中.因此,十分有必要研究一种具有较高精度的锂离子电池电化学简化模型,在保证计算精度的同时,提高计算效率.

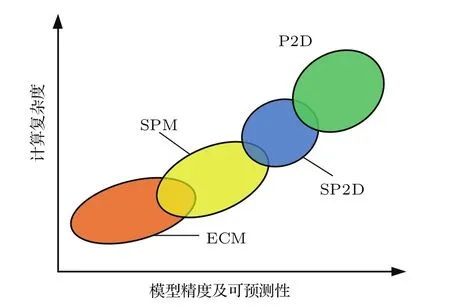
图1 锂离子电池不同模型计算复杂度对比示意图Fig.1.Comparison of different Li-ion battery models with regard to their complexity and predictability.

Subramanian等[19,20]提出基于多项式近似的宏观-微观耦合锂离子电池求解方法,研究表明该方法能减少微分方程的数量,实现锂离子电池电化学行为的实时(毫秒级)仿真模拟和控制,但多项式近似模型仅可简化电池的固相扩散,其耦合的非线性偏微分方程仍需要大量计算.Santhanagopalan等[21]比较了基于物理电化学模型和单粒子模型(single particle model,SPM)的计算效率和仿真结果,表明SPM模型能够在低放电倍率(＜1 C)下快速计算锂电池电化学动力学行为,但由于该模型忽略了锂离子液相浓度分布和液相电势分布,在中高及较高倍率下对电池动力学行为仿真的精度较差.Smith等[22]假定电池具有准线性电化学行为并且其反应电流从液相浓度解耦,进而提出一种面向电化学控制的简化模型,能够对锂电池的开路电压、电极表面浓度和电解液浓度进行模拟.Di Domenico等[23]提出一种降阶的平均电化学模型,并给出方程数值求解方法.Prada等[24]考虑了液相浓度的影响,基于电化学平均模型提出一种简化的电化学热耦合模型.此外,Luo等[15]和Rahimian等[25]针对锂离子电池高倍率充放电要求,扩展了基于物理电化学的SPM模型,Moura等[26,27]开发了一种基于偏微分方程的锂离子电池充电状态与正常状态的观测器,黄亮和李建远[10]提出了一种基于单粒子模型和抛物型偏微分方程的锂离子电池系统建模与故障监测系统设计方法.然而,利用上述模型进行计算时,大多将液相有效扩散系数、液相锂离子电导率以及固相有效电导率定义为常数,且忽略了电解液摩尔活度系数的影响.

为此,本文基于多孔电极理论和浓度理论研究了基于电化学模型的锂离子电池多尺度建模方法,在此基础上提出了一种考虑液相动力学行为的锂电池简化准二维(simpli fied pseudo-twodimensions,SP2D)模型,可快速准确地对锂离子电池恒流、脉冲和城市循环工况的放电行为进行仿真计算和分析.最后通过比较索尼NMC18650锂电池的严格P2D模型和SP2D模型电化学行为,验证了本文所提简化模型的准确性和有效性.

2 基于物理电化学的P2D模型

假定基于电化学的锂离子电池P2D模型是一种恒流等温电化学模型[11],其简化结构如图2所示,锂离子电池包括正负极集流体、正负极涂层以及隔膜等.

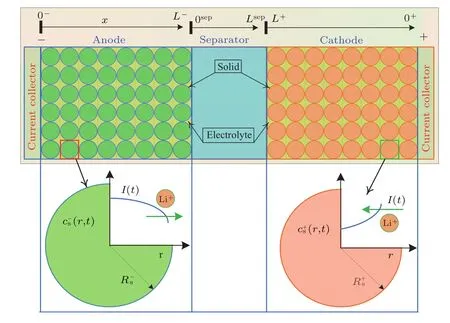
图2 锂离子电池P2D模型示意图Fig.2.Schematic of the electrochemical battery P2D model.

在P2D模型中,正负极集流体电导率非常高从而导致集流体在空间坐标y轴和z轴没有明显的变化,换言之,x轴维度的电化学反应动力学占据电池动力学行为的主导地位.此外,为了解释锂离子在固相和液相的嵌入和脱嵌行为,假设存在一个单一维度的固体球形粒子,重叠于电解液中,而且电池正负电极之间各个区域都存在球形单粒子.锂离子在单粒子颗粒物内的扩散是在球形粒子径向r维度,另外还需要考虑时间维度的信息,因此该模型称为多尺度准二维电化学P2D模型.考虑固相和液相电化学动力学行为以及相界面电化学反应,基于多孔电极理论和浓度理论建立锂离子电池P2D模型的动力学方程.

2.1 固相扩散方程

根据Fick第二定理[28],锂离子固相浓度扩散方程为

进一步推导可得

该方程的边界条件满足(3)—(5)式:

2.2 液相扩散方程

锂离子液相浓度ce(x,t)在x轴上随着锂离子的流量密度的梯度而变化,其动力学方程为

液相浓度扩散方程的边界条件可由下列各式定义:

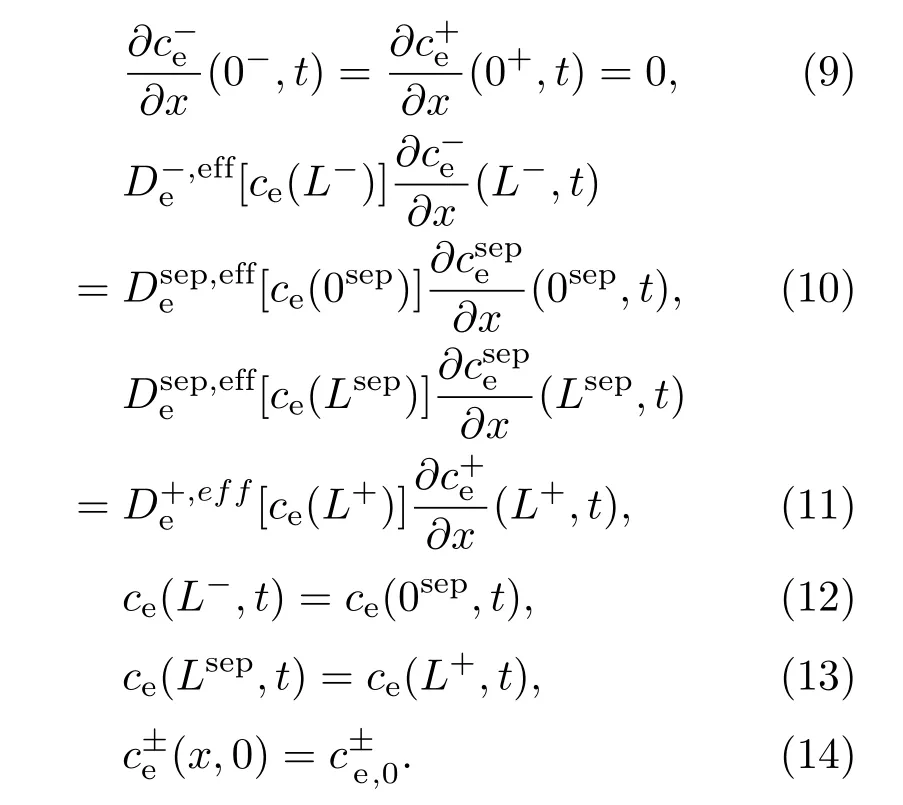
2.3 固相电势方程

锂离子电池内部固相电势ϕs(x,t)的变化采用欧姆定律描述为

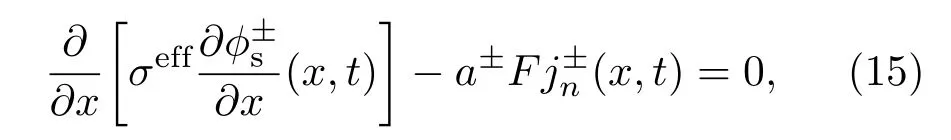
其边界控制条件为

式中,σeff为固相有效导电率,定义为

2.4 液相电势方程

锂离子电池内部液相超电势ϕe(x,t)采用修正的欧姆定律描述为

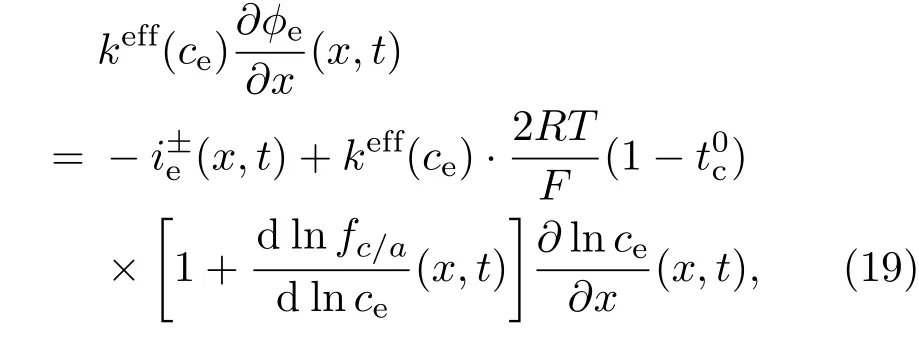
其边界控制条件为

(19)式中,keff是液相浓度ce(x,t)的函数,计算式为

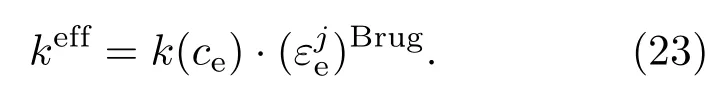
参照文献[5],锂电池不同区域j∈{−,s,+}的液相有效导电率为

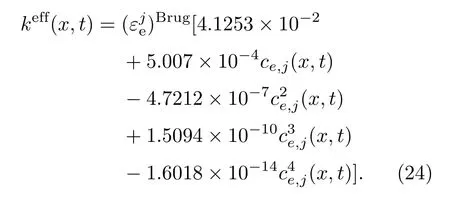
2.5 电荷守恒方程

锂离子电池液相电荷守恒采用法拉第定律描述为

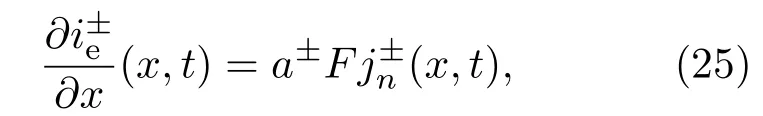
同理,锂离子电池固相电荷守恒描述为

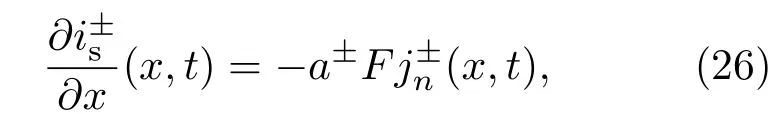
2.6 Bulter-Volmer动力学方程

锂离子电池超电势η±(x,t)依赖于正负极固相电势液相电势正负极开路电压U±以及孔壁通量它们之间的关系为

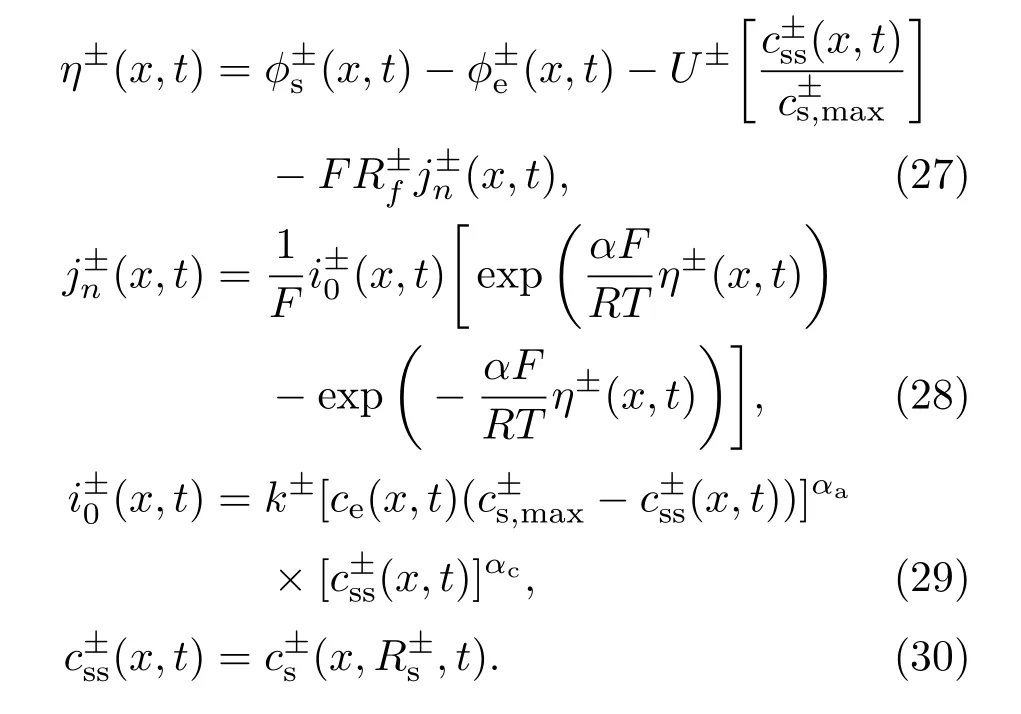
对于锂电池P2D模型来说,输入为工作电流密度I(t),输出为锂电池终端电压,其计算式为

上述公式中涉及的变量及参数所代表的含义如表1.

表1 锂电池参数及相关符号Table 1.Electrochemical model parameters and symbols.

一般情况下,利用有限差分法将固相/液相浓度扩散方程、固相/液相电势方程中的变量离散化可求解锂离子电池数值解.假定将电池正负极、隔膜沿x轴离散化为50个等距节点;正负极电解液中的球形颗粒具有相同的电化学行为,也被离散化为50个等距节点,则对负极而言包括50个液相浓度扩散微分方程、50个液相和固相电势代数方程、一个单粒子有50个固相浓度扩散微分方程,整个负极有50×4=200个微分方程;对于隔膜而言,仅包含液相浓度扩散和液相电势方程,具有50个液相浓度扩散微分方程、50个液相电势代数方程;同样,正极具有50×4=200个微分方程,则严格P2D模型的待求解微分方程数为50×4+50×2+50×4=500个,而且不同方程之间相互有一定耦合.这对于电动汽车动力电池管理系统的实时参数在线估计和控制来说,求解严格P2D模型是比较困难的,而且难以应用于实际中,因此有必要寻找一种能够快速准确求解的简化锂离子电池电化学模型.

3 P2D模型的简化

本节基于扩展的物理电化学SPM模型[11,25]相关假设推证严格P2D模型的简化及其求解过程.考虑锂电子电池电化学反应特性,给出如下模型简化的假设.

假设1正负电极的固相锂离子浓度和锂离子孔壁通量在x轴的任一时刻t为常量,即在x轴上为常量.

假设2在(30)式中,交换电流密度可用不依赖于x轴的交换电流密度的平均值替换.

假设3根据多孔电极理论和浓度理论,液相锂离子摩尔数nLi,e和固相锂离子摩尔数nLi,s是守恒的.结合假设1可知,锂离子孔壁通量正比于电流密度I(t).

假设4(29)和(30)式中的常数αa=αc,且简记为α.

基于上述假设可知,锂离子电池电化学动力学方程包含:1)描述固相浓度扩散的两个线性偏微分方程;2)描述电池不同区域液相浓度扩散的三个准线性微分方程;3)计算电池终端电压的一个非线性方程.根据假设1和(26)式及其边界条件可知锂离子孔壁流量为

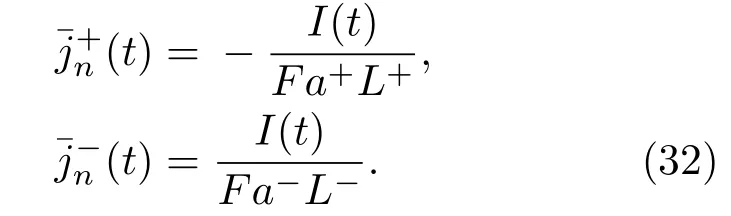
其中,液相电流密度ie(x,t)和孔壁流量密度的变化如图3所示[11].

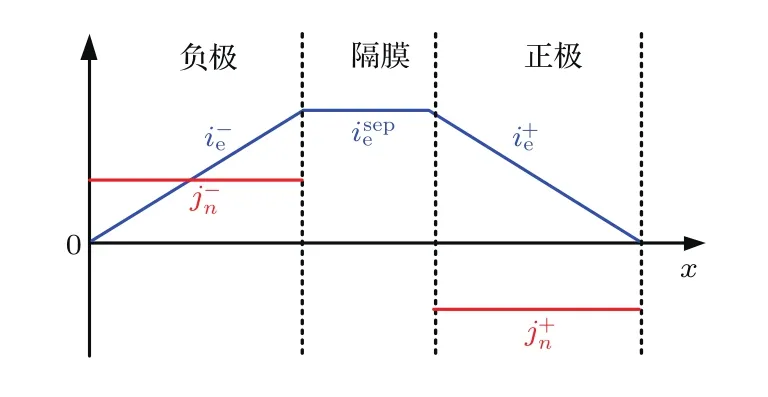
图3 基于本文假设的简化孔壁流量密度和液相电流变化Fig.3.Variation of simpli fied j±n(t)and ije(t)based on some assumptions used in the SP2D model derivation.

将(22)式代入边界控制方程(3)和(4)并结合假设1可推导获得固相浓度扩散方程为:

综合(6),(25)和(32)式及假设1可得液相浓度扩散方程为:

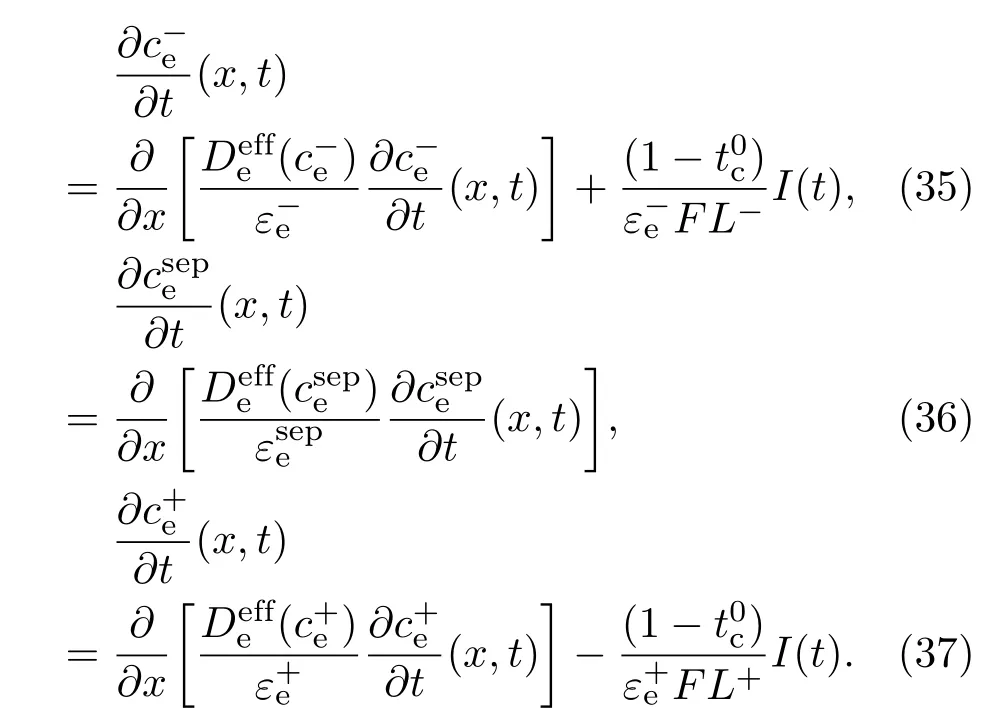
上述微分方程(35)—(36)的边界条件如(9)—(14)式所示.

推导求解电池端电压的非线性计算式.根据(31)式可知,电池端电压V(t)依赖于集流体固相电势因而根据固相电势和相关空间平均量求解(27)式可得

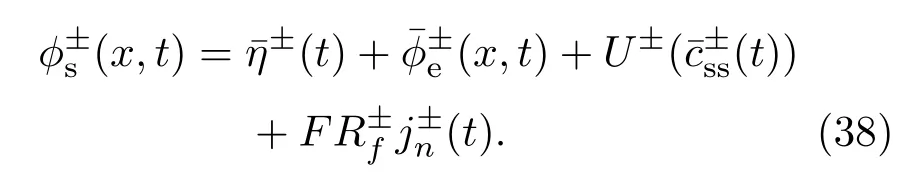
对(38)式右端各子项,分别推导其简化计算式.其中,超电势¯η±(t)可通过求解Bulter-Volmer方程(28)获得,基于假设1、假设2和假设4,并将(32)式代入可得

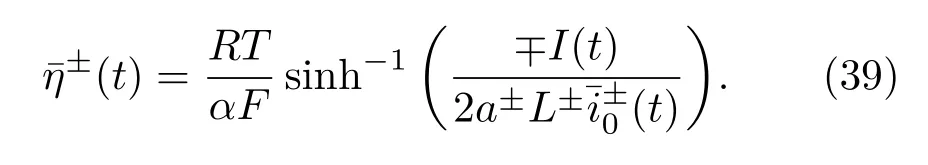
在整个电池厚度x轴上对液相电势微分方程(19)式积分可得平均液相电势即

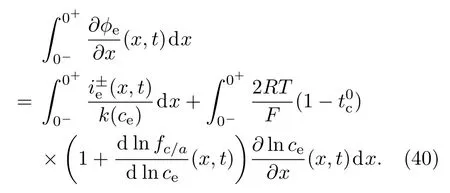
为了获得(40)式数值解析积分值,进一步给出如下假设[27].

假设5计算项在x轴上近似为常量,即kf(t)≈kf(x,t).

假设6计算项k(ce)近似为常量,即¯k=k(ce).由此可得如下表达式:

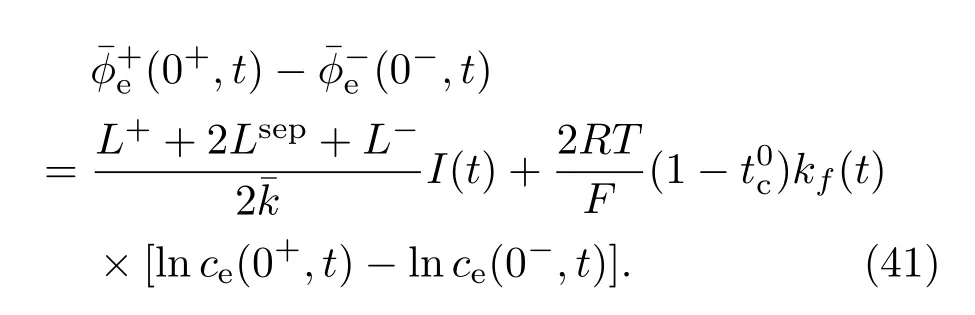
最后,综合(32)和(38)—(41)式可得计算电池

终端电压的表达式为

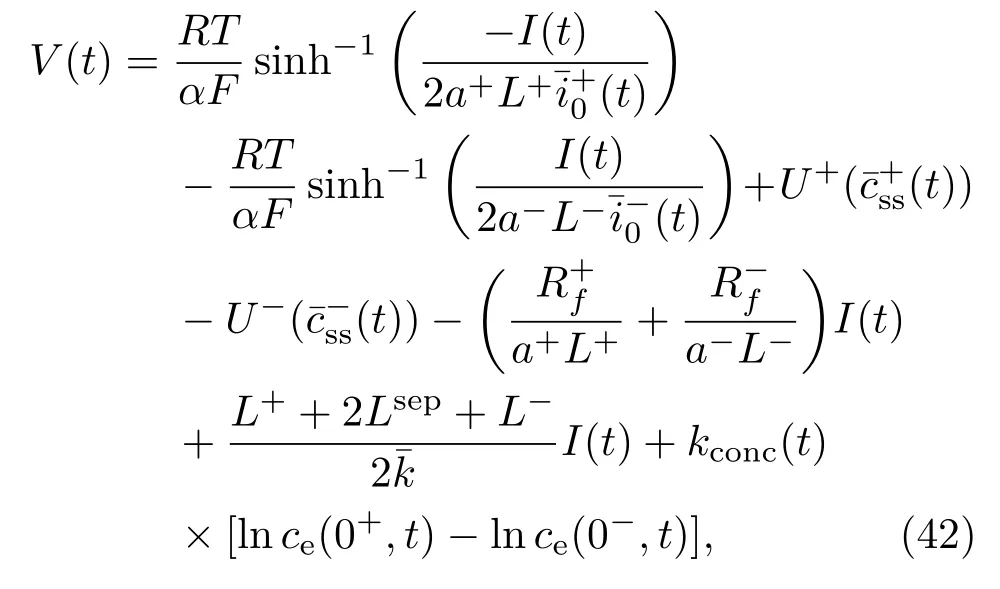
从图4可知,若以第2节的P2D模型的离散数为基准,采用SP2D模型求解锂电池终端电压时,待求解的微分方程数为:50×3=150个液相浓度扩散微分方程,50×2=100个固相浓度扩散微分方程,求解正负极平均超电势的2个代数方程、电池两端集流体平均液相电势代数方程以及计算电池隔膜电压下降的代数方程,共254个方程.由此可见,经过模型简化不仅减少了待求解方程总数而且实现了解耦计算,使得方程数值求解较为容易.

图4 SP2D模型终端电压计算框图Fig.4.Block diagram of the SP2D model for computing battery terminal voltage.

4 模型对比与分析

以索尼NMC18650锂电池为对象,其正极采用镍锰钴三元材料,标称容量720 mAh,平台电压3.7,最小电压2.5 V,最大电压4.2 V,通过对电池的充放电实验获得不同工况下的实验数据,基于遗传算法可以识别出电池主要参数, 即并参考相关文献[12,19,29],给出该电池的参数如表2所列.

表2 索尼NMC18650锂电池参数表Table 2.The parameters lists of Sony NMC 18650 Li-ion battery.

为了验证本文所提出SP2D模型的有效性,基于有限差分法分别计算严格P2D模型和SP2D模型的锂离子电池的电化学放电行为特性,图5—图8分别为相应的计算结果对比曲线,其中,图6和图7的横纵坐标分别为归一化的离散点和液相浓度值,1 C恒流放电倍率的电流密度为20 A/m2.

由图5可知,相较于严格P2D模型,SP2D模型能够在不同放电倍率下模拟锂离子电池终端电压变化,而且与严格P2D模型计算结果符合良好.经过计算,不同放电倍率下的两种模型的输出电压最大相对误差为1.55%.

图5 (网刊彩色)不同放电倍率下的电池端电压对比曲线Fig.5.(color online)Comparisons of the battery voltage at various C-rates discharge.

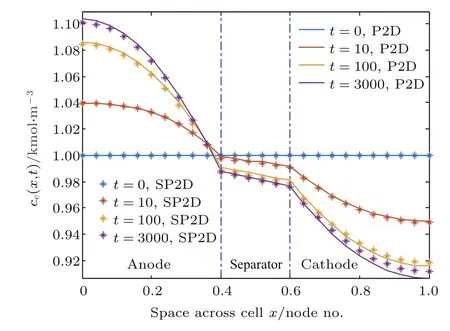
图6 (网刊彩色)1 C放电倍率下不同时刻液相锂离子浓度分布Fig.6.(color online)Li-ion electrolyte concentration at different time at 1 C-rate discharge.

图7 (网刊彩色)1 C放电倍率下电池不同节点液相锂离子浓度分布Fig.7.(color online)Li-ion electrolyte concentration at the current collector and electrode-separator interfaces at 1 C-rate discharge.

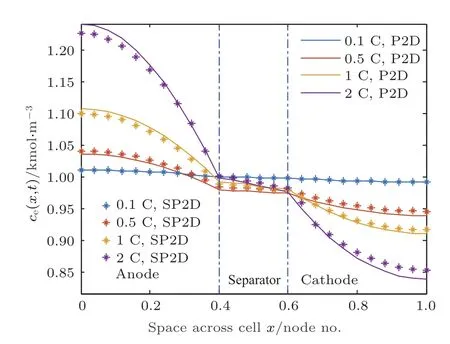
图8 (网刊彩色)不同放电倍率下仿真结束时的液相锂离子浓度分布Fig.8.(color online)Li-ion electrolyte concentration at the end-of-simulation at various C-rate discharge.

观察图6—图8可知,相较于严格的P2D模型,SP2D模型能够预测并模拟锂离子电池液相放电行为特性,特别是在同一放电倍率下对于不同时刻和电池厚度的不同节点以及不同放电倍率下的液相锂离子浓度分布都具有很好的仿真.此外,在不同放电倍率下的仿真结束时刻,两种模型的液相浓度最大相对误差为3.49%.在1 C放电倍率下,利用DellTMW3530 Dual 2.80 GHz台式机在Matlab软件中分别计算P2D模型和SP2D模型的时间为84.9 s和7.2 s,计算时间缩短91.5%,表明在不损失计算精度前提下,SP2D模型可大大缩短计算时间.

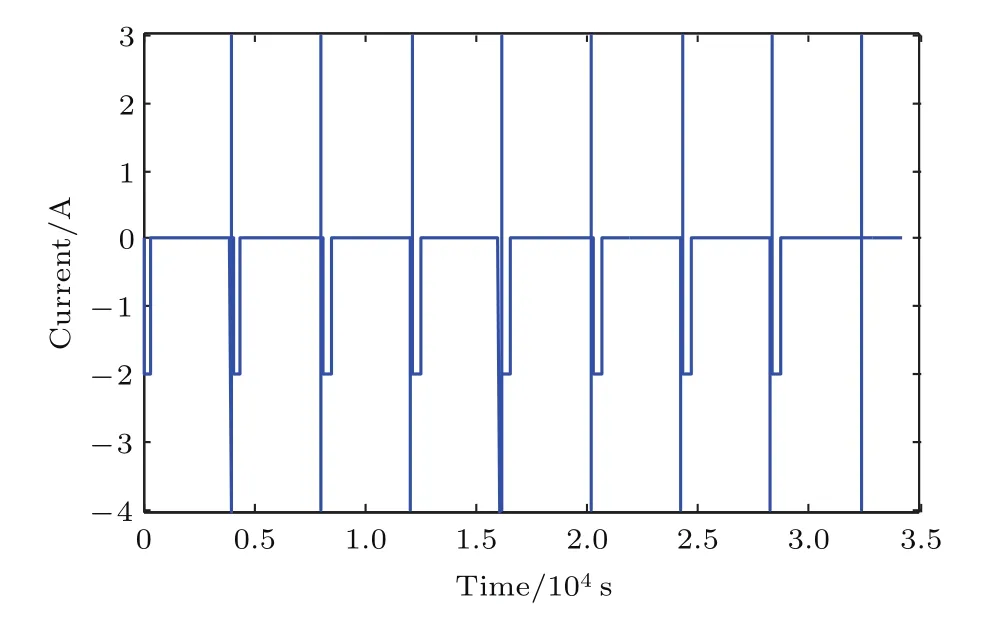
图9 HPPC工况下的脉冲输入电流Fig.9.Pulse input current of HPPC condition.

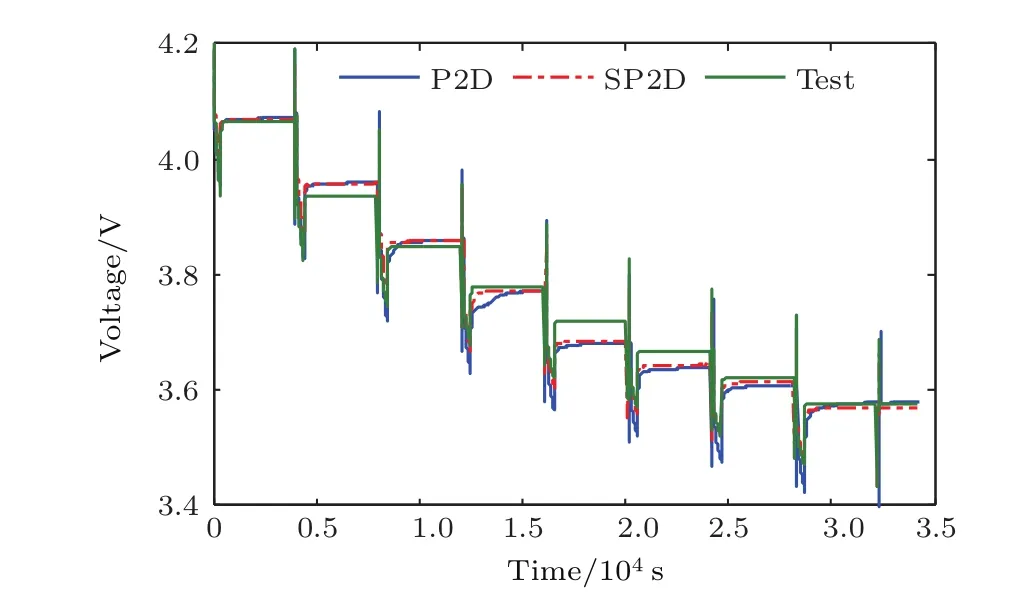
图10 (网刊彩色)HPPC工况下的电池端电压对比曲线Fig.10.(color online)Comparisons of the battery voltage under HPPC condition.

为进一步验证分析SP2D模型的有效性,将NMC18650锂电池在室温23°C下进行HPPC(hybrid pulse power characterization)和US06(urban dynamometer driving schedule)工况仿真计算.其中,图9和图11为电池仿真计算和实验测试所用的输入电流,图10和图12为两种模型计算的电池终端电压和实验数据的对比结果.从图10和图12可以看出,SP2D模型能够准确仿真HPPC和US06工况下电池终端电压的变化趋势,经过计算其输出电压最大相对误差分别为2.14%和2.37%.由于脉冲放电和循环变电流可以削弱锂离子电池正极/负极电极的极化现象[30],延长电池使用时间,因此在同样时间内,锂电池在HPPC和US06工况下仍能工作在平台电压范围内,表明SP2D模型能准确描述电池内部的扩散和极化现象.

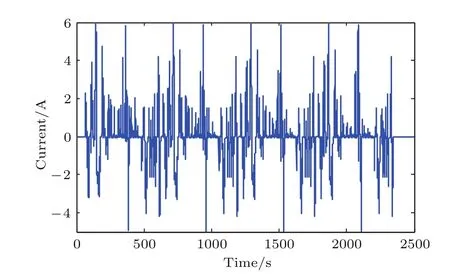
图11 US06工况输入电流Fig.11.Input current of US06 condition.

图12 (网刊彩色)US06工况下的电池端电压对比曲线Fig.12.(color online)Comparisons of the battery voltage under US06 condition.

5 结 论

1)基于多孔电极理论和浓度理论,建立了宏观-微观、时间-空间的多尺度锂离子电池物理电化学模型,基于该模型提出了一种考虑锂离子液相动力学的简化准二维模型.

2)通过将严格P2D模型进行简化,使得待求解的微分方程总数减少近一半,在保证计算精度的前提下,提高计算效率90%左右,这对于电池管理系统的参数在线估算以及实时控制具有重要意义.

3)相较于严格P2D模型,本文提出的SP2D模型在2 C,1 C,0.5 C和0.1 C恒流放电工况下能够准确预测锂电池的端电压和锂离子浓度变化,其最大相对误差分别为1.55%和3.49%;同时,在HPPC和US06工况下亦可精确计算模拟锂电池端电压,且最大相对误差分别为2.14%和2.37%.

4)下一步将开展基于SP2D模型的锂电子电池荷电状态估计和电化学与热能耦合关系的相关研究,进一步预测电池内部温度分布以及电化学行为.

感谢美国克莱姆森大学国际汽车研究中心刘子凡博士给予的支持.

[1]Wang M,Li J J,Wu H,Wan C R,He X M 2011J.Power Sources7 862(in Chinese)[王铭,李建军,吴扞,万春荣,何向明2011电源技术7 862]

[2]Cheng J,Li Z,Jia M,Tang Y W,Du S L,Ai L H,Yin B H,Ai L 2015Acta Phys.Sin.64 210202(in Chinese)[程昀,李劼,贾明,汤依伟,杜双龙,艾立华,殷宝华,艾亮2015物理学报64 210202]

[3]Wang J P,Guo J G,Ding L 2009Energy Convers.Manag.50 318

[4]Fleischer C,Waag W,Bai Z,Sauer D U 2013J.Power Sources243 728

[5]Domenico D D,Stefanopoulou A,Fiengo G 2010J.Dyn.Sys.Meas.Control132 768

[6]Prada E,Domenico D D,CreffY,Bernard J,Sauvant-Moynot V,Huet F 2012J.Electrochem.Soc.159 A1508

[7]Prada E,Domenico D D,CreffY,Bernard J,Sauvant-Moynot V,Huet F 2013J.Electrochem.Soc.160 A616

[8]Chaturvedi N A,Klein R,Christensen J,Ahmed J,Kojic A 2010Control Syst.IEEE30 49

[9]Guo M,Sikha G,White R E 2011J.Electrochem.Soc.158 A122

[10]Huang L,Li J Y 2015Acta Phys.Sin.64 108202(in Chinese)[黄亮,李建远 2015物理学报 64 108202]

[11]Kemper P,Li S E,Kum D 2015J.Power Sources286 510

[12]Han X,Ouyang M,Lu L,Li J 2015J.Power Sources278 814

[13]Guo M,Jin X F,White R E 2017J.Electrochem.Soc.164 E3001

[14]Doyle M,Newman J 1995Electrochim.Acta40 2191

[15]Luo W L,Lu C,Wang L X,Zhang L Q 2013J.Power Sources241 295

[16]Joel C F,Saeid B,Jeffrey L S,Hosam K F 2011J.Electrochem.Soc.158 A93

[17]Venkat R S,Vijayasekaran B,Venkatasailanathan R,Mounika A 2009J.Electrochem.Soc.156 A260

[18]Cai L,White R E 2009J.Electrochem.Soc.156 A154

[19]Subramanian V R,Diwakar V D,Tapriyal D 2005J.Electrochem.Soc.152 A2002

[20]Subramanian V R,Boovaragavan V,Diwakar V D 2007Electrochem.Solid-State Lett.10 A255

[21]Santhanagopalan S,Guo Q Z,Ramadass P,White R E 2006J.Power Sources156 620

[22]Smith K A,Rahn C D,Wang C Y 2007Energy Convers.Manag.48 2565

[23]Di Domenico D,Stefanopoulou A,Fiengo G 2010J.Dyn.Syst.Meas.Control132 061302

[24]Prada E,Domenico D D,CreffY,Bernard J,Sauvant-Moynot V,Huet F 2012J.Electrochem.Soc.159 A1508

[25]Rahimian S K,Rayman S,White R E 2013J.Power Sources224 180

[26]Moura S J,Chaturvedi N A,Krstic M E 2013J.Dyn.Sys.Meas.Control136 011015

[27]Moura S J,Argomedo F B,Klein R,Mirtabatabaei A,Krstic M 2017IEEE Trans.Contr.Syst.T.2 453

[28]Diwakar V D 2009Ph.D.Dissertation(St.Louis:Washington University)

[29]Fan G,Pan K,Canova M,Marcicki J,Yang X G 2016J.Electrochem.Soc.163 A666

[30]Ma J H,Wang Z S,Su X R 2013J.Power Supply1 30(in Chinese)[马进红,王正仕,苏秀蓉2013电源学报1 30]

Multi-scale modeling and its simpli fication method of Li-ion battery based on electrochemical model∗

Pang Hui†

(School of Mechanical and Precision Instrument Engineering,Xi’an University of Technology,Xi’an 710048,China)

19 May 2017;revised manuscript

31 August 2017)

It is very important to accurately model Li-ion battery and estimate the corresponding parameters that can be used for battery management system(BMS)of electric vehicles(EVs).However,the rigorous pseudo-two-dimensional(P2D)model of Li-ion battery is too complicated to be adopted directly to online state estimation and real-time control of stage-of-charge in BMS applications.To solve this problem,in this study we present a simpli fied pseudo-two-dimensional(SP2D)model by the electrolyte dynamic behaviors of electrochemical battery model,which is based on the porous electrode theory and concentration theory.First,the classical concentration equations of Li-ion battery P2D model are investigated and introduced,based on which,the approximated method of describing the concentration distributions of Li-ion battery described by the SP2D model is given by ignoring the variation of Li-ion wall flux density across the electrode thickness;then,the Li-ion battery terminal output voltage,the solid phase concentration and potential diffusion,the electrolyte concentration and potential distribution can be calculated based on the averaged electrochemical dynamic behaviors of Li-ion battery.Moreover,by employing some concentration assumptions:1)the solid-phase lithium concentration in each electrode is constant in spatial coordinatex,and uniform in time;2)the exchange current density can be approximated by its averaged value;3)the total amount of lithium in the electrolyte and in the solid phase is conserved;with the averaged dynamics of SP2D model,the simpli fied calculation expression for Li-ion battery terminal voltage is derived.Finally,a case study of Sony NMC 18650 Li-ion battery is conducted,and the simulated comparisons among the battery voltages at different-C-rate galvanostatic discharges,and the related electrolyte concentration of Liion at 1 C-rate are conducted.Moreover,the proposed SP2D model is used to predict the battery voltage and electrolyte concentration distribution with respect to the P2D model under hybrid pulse power characterization condition and urban dynamometer driving schedule condition,and the corresponding test data are used to verify the accuracy of the SP2D model.It is observed that the simulated data of SP2D model are in good accord with those of the P2D model and test curve under these two operation conditions,which further validates the effectiveness of the proposed electrochemical model of Li-ion battery.Accordingly,the proposed SP2D model in this paper can be used to estimate real-time state information in advanced battery management system applications,and can improve the calculation efficiency significantly and still hold higher accuracy simultaneously than that from the P2D model.

electric vehicles,Li-ion batteries,electrochemistry,model reduction

PACS:88.85.Hj,82.47.Aa,82.80.Fk,95.75.—zDOI:10.7498/aps.66.238801

*Project supported by the National Natural Science Foundation of China(Grant No.51675423).

†Corresponding author.E-mail:huipang@163.com

(2017年5月19日收到;2017年8月31日收到修改稿)

锂离子电池的精确建模和状态估计对于电动汽车电池管理系统非常重要,准二维(P2D)电化学模型由于计算复杂,难以直接应用于电池管理的参数在线估计和实时控制中.本文基于多孔电极理论和浓度理论,提出一种考虑锂离子液相动力学的简化准二维(SP2D)模型.忽略锂离子孔壁流量沿电极厚度方向的变化求解SP2D模型所描述的锂离子电池锂浓度分布,基于锂离子电池电化学平均动力学行为求解固相和液相电势变化,推导出电池电压计算的简化表达式;采用恒流、脉冲以及城市循环工况放电电流对比分析了严格P2D模型与SP2D模型的终端电压和浓度分布.结果表明:SP2D模型在保持较高计算精度的同时,可显著提高计算效率.

10.7498/aps.66.238801∗国家自然科学基金(批准号:51675423)资助的课题.

†通信作者.E-mail:huipang@163.com