多寡头不同成本古诺模型的纳什均衡分析
2017-12-25冯晶晶
冯晶晶,胡 艳
(西安培华学院智能科学与信息工程学院,陕西 西安 710125)
多寡头不同成本古诺模型的纳什均衡分析
冯晶晶,胡 艳
(西安培华学院智能科学与信息工程学院,陕西 西安 710125)
将古诺的双寡头垄断模型推广到多个寡头垄断的情形,分析了多寡头古诺博弈的纳什均衡,用最优化和初等变换等数学方法得到了纳什均衡解.在此基础上,将古诺的双寡头垄断模型中相同的边际成本推广到不同的边际成本,讨论了不同成本的双寡头古诺博弈的纳什均衡,得到其纳什均衡解.
古诺模型;n寡头;不同成本;纳什均衡
法国经济学家古诺1838年在《财富理论的数学原理研究》中对寡头垄断的一种极端形式——双寡头垄断作了分析研究.古诺模型是最早对战略依存的经济现象进行研究并提出均衡解的经济学模型,但该模型只是在特定的垄断情况下,两个寡头同时进行产量决策,在不存在固定成本、边际成本为常数的情况下得到博弈的纳什均衡.大多数文章[1-5]直接应用古诺模型对市场进行分析,采用数学方法对古诺模型理论[6-9]进行研究的较少.本文就古诺模型的理论进行研究,一方面将古诺的双寡头垄断模型推广到n个寡头的情形,另一方面将古诺的双寡头垄断模型中相同的边际成本推广到不同的边际成本,并得到这两种博弈的纳什均衡.
1 预备知识
博弈的标准形式[10]表述包括:1)博弈的参与者.参与者从1到n排序,设任一参与者的序号为i.2)每一参与者可供选择的战略集.令Si代表参与者i的战略空间,其中任意一个特定的战略用si表示,si∈Si.3)针对所有参与者可能选择的战略组合,每一个参与者获得的收益.令(s1,s2,…,sn)表示每个参与者选定一个战略形成的战略组合,ui表示第i个参与者的收益函数,ui(s1,s2,…,sn)即为参与者选择战略(s1,s2,…,sn)时第i个参与者的收益.
定义1[10]在一个n人博弈的标准式表述中,参与者的战略空间为S1,S2,…,Sn,收益函数为u1,u2,…,un,用G={S1,S2,…,Sn;u1,u2,…,un}表示此博弈.
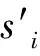
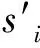
对其他参与者在战略空间S1,…,Si -1,Si +1,…,Sn中每一组可能的战略(s1,…,si -1,si +1,…,sn)都成立.
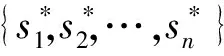
2 主要结果
2.1 n寡头古诺博弈中的纳什均衡
假定古诺的寡头模型中有n个企业,令qi代表企业i的产量,且Q=q1+q2+…+qn表示市场总产量,p表示出清价格,并假设反需求函数由P(Q)=a-Q给出(设Q 现求n寡头古诺博弈中的纳什均衡解.首先将该博弈化为标准式的博弈,n寡头垄断模型中有n个参与人,即模型中有n个垄断企业,由于产出不可能为负,每一企业的战略空间就可表示为Si=[0,+),其中一个代表性战略si就是企业选择的产量,qi≥0,特别大的产量是不可能的,不应包括在战略空间中,但由于Q≥a时,P(Q)=0,任一企业都不会有qi>a的产出.其次,需要把企业i的收益表示为它自己和另一企业所选择战略的函数. 假定企业的收益就是其利润额,这样在一般的n个参与者标准式博弈中,参与者i的收益ui(s1,s2,…,sn)就可写为: 在古诺的n头垄断模型中,上面的条件可具体表述为一对产出组合. 再考虑在古诺双头垄断模型中,反需求函数为P(Q)=a-Q,c1为企业1的边际成本,c2为企业2的边际成本,且c1≠c2.模型中的两个垄断企业为两参与人,产品的产量为每个企业可选择的战略.每个企业的战略空间可表示为Si=[0,+),即包含所有非负实数,其中一个代表性战略si就是企业选择的产量,qi≥0.要全面表述这一博弈并求其均衡解,还需把企业i的收益表示为它自己和另一企业所选择战略的函数,假定企业的收益就是其利润额,这样在一般的两个参与者标准式博弈中,参与者i的收益ui(si,sj)可写为πi(qi,qj)=qi[p(qi+qj)-ci]=qi[a-(qi+qj)-ci].其中0 本文将双寡头古诺垄断模型推广到多个寡头垄断,用最优化和初等变换等数学方法得到了纳什均衡解,并得到当寡头无限增多时,总产量无限趋于a-c.另一方面,将古诺的双寡头垄断模型中相同的边际成本推广到不同的边际成本,得到其纳什均衡解.该结果更加贴近地反映市场的运营情况,给市场运营提供了一定的理论基础. [1] 王静,周学立.纵向产品差异化市场古诺博弈模型的稳定性分析[J].辽宁师范大学学报(自然科学版),2015,38(4):460-463. [2] 计晓静,赵自强,沙莎.供应链竞争下的需求风险和汇率风险传导研究:基于古诺模型[J].南京师范大学学报(工程技术版),2015,15(4):82-89. [3] 叶子,令狐大智.双寡头竞争环境下的碳配额分配策略研究[J].系统工程理论与实践,2015,35(12):3038-3045. [4] 何春燕.基于博弈论的我国稀土出口政策研究[D].北京:中国地质大学,2013. [5] 李佼瑞,昌健.确定和不确定策略框架下的古诺双寡头模型[J].系统工程学报,2015,30(5):594-600. [6] 陈东立,姚杰,史艳维.基于纯策略的区间数矩阵博弈模型的研究[J].重庆理工大学学报(自然科学版),2012,26(2):107-111. [7] 张明善,唐小我.多个生产商下的动态古诺模型分析[J].管理科学学报,2002,5(5):85-90. [8] 姚洪兴,张芳.差异化策略的两组动态古诺模型及其稳定性控制[J].江苏大学学报(自然科学版),2012,33(3):364-368. [9] 胡振华,胡东滨.寡头垄断市场古诺模型的研讨[J].中南工业大学学报,1997,28(1):99-102. [10] 罗伯特·吉本斯.博弈论基础[M].北京:中国社会科学出版社,1999. TheNashEquilibriumAnalysisofMultiOligopolyCournotModelwithDifferentCost FENG Jingjing, HU Yan (School of Intelligent Science and Information Engineering, Xi’an Peihua University, Xi’an 710125, China) The Cournot duopoly model is generalized to multiple oligopoly monopoly model, the Nash equilibrium of multiple oligopoly Cournot game is analyzed, and Nash equilibrium solution is obtained with optimization and elementary transformation mathematical methods. On this basis, the same marginal cost in the Cournot duopoly model is extended to different marginal cost, the Nash equilibrium of the duopoly Cournot game with different cost is discussed, then the Nash equilibrium solution is obtained. Cournot model;noligopoly; different cost; Nash equilibrium 2017-03-17 国家自然科学基金项目(61473239);陕西省教育厅专项科学研究项目(2015JK2093);西安培华学院校级课题项目(PHKT17028). 冯晶晶(1984-),女,讲师,硕士,主要从事非标准分析理论和金融数学研究.E-mail:fengjingjing0105@163.com 10.3969/j.issn.1674-232X.2017.06.017 O29;F224.32MSC201091A06;91A13 A 1674-232X(2017)06-0665-03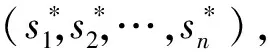

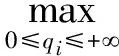


2.2 不同成本的双寡头古诺博弈的纳什均衡

3 结论
