双分数跳-扩散过程下汇率连动期权定价

刘淑琴，薛 红

(西安工程大学理学院，陕西 西安 710048)

双分数跳-扩散过程下汇率连动期权定价

刘淑琴，薛 红

(西安工程大学理学院，陕西 西安 710048)

假定股价和汇率分别满足双分数跳-扩散过程，期望收益率、无风险利率和波动率均为常数，建立双分数跳-扩散过程下金融市场数学模型，运用保险精算方法，得到了双分数跳-扩散过程下汇率连动期权定价公式.

双分数布朗运动；跳-扩散过程；保险精算；汇率连动期权

0 引言

近年来，不少学者对汇率连动期权进行了研究，其定价不仅依赖于外国股票的价格，而且依赖汇率的变化.作为进行全球投资的一种金融期权形式，汇率连动期权定价越来越引起金融领域的重视.文献[1]在布朗运动环境下基于无套利、均衡、完备的假设，利用复制的思想得到了汇率连动期权的平价公式，但当市场是有套利、非均衡、不完备时，传统的期权定价方法将无法使用；文献[2-3]在布朗运动环境下利用保险精算方法分别给出了汇率连动期权定价式和跳跃过程下的汇率连动期权的定价公式；文献[4]设计了一种重设型熊市汇率连动股票卖权，用鞅定价方法给出其定价公式；文献[5]通过所谓的平方根汇率连动远期契约，利用鞅定价方法给出汇率连动远期契约定价公式；文献[6]在布朗运动环境下用鞅方法讨论了汇率连动期权定价；文献[7]在单因素HJM结构下利用等价鞅测度讨论了两种汇率连动期权，得到了两种看涨期权价格的精确解；文献[8]在市场满足无套利和风险中性的条件下，外国股票和汇率遵循布朗运动，研究了欧式幂型期权的鞅定价问题；文献[9]在几何布朗运动假设条件下，利用鞅定价方法求出汇率连动股票期权的到期收益，并将它的定价公式设计成幂函数的形式；文献[10]在分数布朗运动环境下利用偏微分方程方法讨论了分数布朗运动环境下的汇率连动期权定价；文献[11]提出了双分数布朗运动，是分数布朗运动的一种推广，可以描述比分数布朗运动更一般的金融现象；文献[12]研究了双分数跳-扩散环境下欧式期权的定价问题.保险精算方法[13]在期权定价中最为常用，适用于任何金融市场.本文在股价满足双分数跳-扩散过程下，利用保险精算方法推导出双分数跳-扩散下汇率连动期权定价.

1 双分数布朗运动环境下金融市场模型

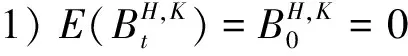
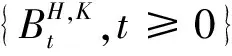
假设股票价格{St,t≥0}，汇率动态价格{Xt,t≥0}分别满足方程

(1)

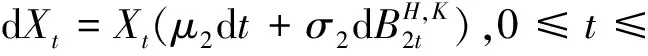
(2)

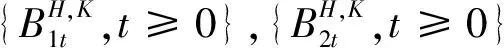
引理1[12]随机微分方程(1)，(2)的解分别为

(3)

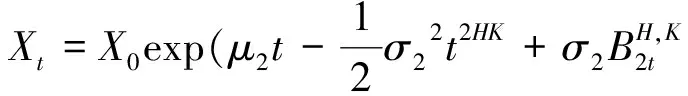
(4)

定义2[12]股票价格过程{St,t≥0}在[t,T]的期望回报率βu，u∈[t,T]定义为

引理2[12]在概率空间P下，{St,t≥0}在[0,T]上的期望收益率为

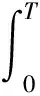
同理,{Xt,t≥0}在[0,T]上的期望收益率为

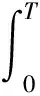
引理3[14]设随机变量ξ1～N(0,1)，ξ2～N(0,1)，Cov(ξ1,ξ2)=ρ，则对任意实数a,b,c,d,k,有

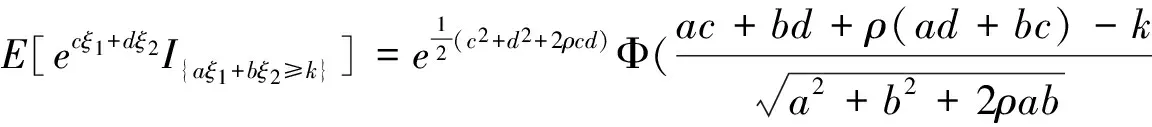
2 汇率连动期权定价

2.1 第一种汇率连动期权

第一种汇率连动期权的损益η1=(STXT-k)+,其中T为到期日，k(本国货币)为执行价格.用C10(k,T)表示到期日为T,执行价格为k(本国货币)的欧式看涨汇率连动期权在零时刻的保险精算价格为

C10(k,T)=E{[exp(-μ2T)XTexp(-μ1T)ST-kexp(-rdT)]IA}.

其中A={exp(-μ2T)XTexp(-μ1T)ST>kexp(-rdT)}.

定理1具有损益η1=(STXT-k)+的汇率连动期权在到期日为T,执行价格为k(本国货币)的欧式看涨汇率连动期权在零时刻的保险精算价格

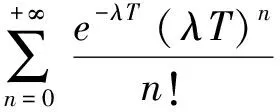
其中

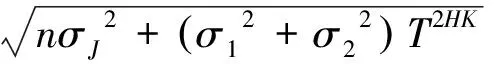
N(·)表示标准正态随机变量的分布函数.

证明首先，A={exp(-μ2T)XTexp(-μ1T)ST>kexp(-rdT)}.令

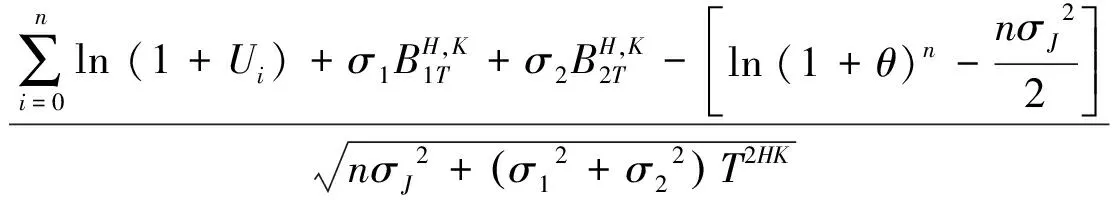
则A={ξ>d}.从而

C10(k,T)=C11-C12,

那么

从而得到第一种汇率连动看涨期权定价公式

同理可求得汇率连动看跌期权在零时刻的定价公式.

2.2 第二种汇率连动期权

第二种汇率连动期权的损益η2=XT(ST-k)+，其中T为到期日，k(国外货币)为执行价格.用C20(k,T)表示到期日为T，执行价格为k的欧式看涨汇率连动期权在零时刻的保险精算价格：

C20(k,T)=E[XTe-μ2T(STe-μ1T-ke-rfT)IB],

其中B={STe-μ1T>ke-rfT}.

定理2具有损益η2=XT(ST-k)+的汇率连动期权在到期日为T，执行价格为k的看涨期权价格

其中

证明首先，B={STe-μ1T>ke-rfT}.令

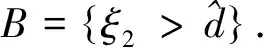
先求

(5)

利用引理3，式(5)化简为

那么

同理，

因此，

同理可求得第二种汇率连动看跌期权在零时刻的定价公式.

2) 当K=1时，可得分数跳-扩散环境下汇率连动期权定价公式.

3 小结

当前汇率连动期权渐渐吸引了国内外许多投资人的眼球，其定价也越来越引起人们的重视.有越来越多的证券投资商以及各种商业银行发行了此种期权，但由于股价以及汇率的变动都是随机的过程，对其定价相对来说有一定的难度，因此本文利用保险精算进行贴现定价方法定价了此种期权，不论金融市场处于以上何种情况，本文给出的汇率连动期权公式都能使用.

[1] REINER E. Quanto mechannics[J]. Risk,1992(3):59-63.

[2] 张元庆，蹇明．汇率连动期权的保险精算定价[J]．经济数学，2005，22(4)：363-367．

[3] 张元庆，闻德美，刘美娟．跳跃过程下的汇率连动期权的定价[J]．经济数学，2010，27(1)：67-72．

[4] 田存志．重设型熊市汇率连动股票卖权的创新与定价研究[J]．管理工程学报，2006，20(2)：130-133．

[5] 李兴绪．汇率连动远期协议的创新及定价[J]．云南财贸学院学报，2004，20(2)：47-51．

[6] 陈松男．金融工程学[M]．上海：复旦大学出版社，2002．

[7] 李淑锦．在单因素HJM结构下定价两种汇率连动期权[J]．应用数学，2008，21(2)：384-389．

[8] 刘敬伟．汇率连动欧式幂型期权鞅定价及避险[J]．数学的实践与认识，2010，40(14)：1-8．

[9] 张恒．幂函数重设型汇率连动股票期权的定价[D]．上海：华东师范大学，2009．

[10] XUE H, HUANG K Y. Quanto option pricing in fractional motion environment[C]//The 3rd International Conference on Engineering and Business Management. Wuhan：[s.n.],2012:2959-2962.

[11] RUSSO F, TUDORB C A. On the bifractional brownian motion[J]. Stochastic Processes and Applications,2006,116(5):830-856.

[12] XUE H, WU J Z. Pricing European option under bi-fractional ump-diffusion process[C]//The 3rd International Conference on Advanced Information and Communication Technology for Education. Guangzhou:[s.n.],2015:267-270.

[13] BLADT M, RYDBERG T H. An actuarial approach to option pricing under the physical measure and without market assumptions[J]. Insurance Mathematics & Economics,1998,22(1):65-73.

[14] 刘坚，文风华，马超群．欧式期权和交换期权在随机利率及O-U过程下的精算定价方法[J]．系统工程理论与实践，2009，29(12)：118-124．

TheQuantoOptionPricingModelinBi-fractionalJump-diffusionProcess

LIU Shuqin， XUE Hong

(School of Science, Xi’an Polytechnic University, Xi’an 710048, China)

Assume that the stock price and exchange rate satisfies the bi-fractional jump-diffusion process, the expected return rate, risk-less interest rate and the volatility rate are constants. The financial market mathematical model is built by the stochastic analysis for bi-fractional jump-diffusion process. Using the actuarial approach, the pricing formula of Quanto option is obtained.

bi-fractional Brownian motion; jump-diffusion process; actuarial mathematics; Quanto option

2017-02-17

陕西省自然科学基础研究计划项目(2016JM1031)；西安工程大学研究生创新基金资助项目(CX201712).

薛 红(1964-)，男，教授，博士，主要从事随机分析及金融工程等研究.E-mail:xuehonghong@sohu.com

10.3969/j.issn.1674-232X.2017.06.016

F830；O211MSC201091G20

A

1674-232X(2017)06-0659-06