渐近伪压缩映象迭代序列收敛的等价性

赵美娜，张树义，金 珩

(1. 渤海大学数理学院,辽宁 锦州 121013； 2. 内蒙古师范大学数学科学学院,内蒙古 呼和浩特 010022)

渐近伪压缩映象迭代序列收敛的等价性

赵美娜1，张树义1，金 珩2

(1. 渤海大学数理学院,辽宁 锦州 121013； 2. 内蒙古师范大学数学科学学院,内蒙古 呼和浩特 010022)

在没有任何有界的条件下，在实Banach空间中研究依中间意义渐近非扩张的渐近伪压缩映象具混合误差修正的Ishikawa和修正的Mann迭代序列收敛的等价性, 推广和改进了有关文献中的相应结果.

实Banach空间；渐近伪压缩映象；依中间意义渐近非扩张映象；具混合误差修正的Ishikawa迭代序列；具混合误差修正的Mann迭代序列

1 引言与预备知识

设E是实Banach空间,E*是E的对偶空间,正规对偶映象J:E→2E*定义为J(x)={f∈E*;〈x,f〉=‖x‖2=‖f‖2}，其中〈·,·〉表示E和E*的广义对偶组.用D(T)和F(T)分别表示映象T的定义域和不动点集.

显然，若T:D(T)⊂E→E是渐近非扩张映象，则T是渐近伪压缩映象.但其逆一般不真，反例见文[1].

定义2设D是E的非空凸子集，T：D→D是一映象，x0,w0∈D是任意给定两点，由下式定义的序列{xn}n≥0⊂D,{yn}n≥0⊂D,

(1)

由下式定义的序列{wn}n≥0⊂D，

wn+1=(1-αn-γn-μn)wn+αnTnwn+γnun+μnpn，∀n≥0

(2)

称为具混合误差修正的Mann迭代序列.

下面引理是已知的.

引理1设E是任意实Banach空间，J:E→2E*是正规对偶映象，则∀x,y∈E，有

‖x+y‖2≤‖x‖2+2〈y,j(x+y)〉,∀j(x+y)∈J(x+y).

文[1]在Banach空间的框架下，研究了依中间意义渐近非扩张的渐近伪压缩映象具误差修正的Ishikawa和修正的Mann迭代序列收敛的等价性问题.文[2]推广、改进了文[1]中的结果.文[3-17]研究了一些非线性映象不动点的存在性与迭代逼近.受上述工作启发，本文进一步研究渐近伪压缩映象具误差修正的Ishikawa和修正的Mann迭代序列收敛的等价性问题,从以下4方面对文[2]中的定理2进行推广和改进：

1)去掉{xn}有界性；

3)将一致光滑Banach空间扩展到实Banach空间，并将

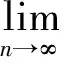
替换成

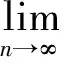
2 主要结果

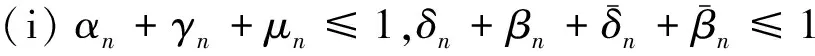
(ii)αn→0，βn→0，δn→0(n→∞)；

设x0=w0∈D是一给定的点，q∈F(T)，{xn}n≥0，{wn}n≥0分别是由式(1)和(2)定义的具混合误差修正的Ishikawa和修正的Mann迭代序列，若存在严格增加函数φ:[0,+∞)→[0,+∞)，φ(0)=0，使得

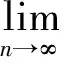
(3)

则xn→q∈F(T)和wn→q∈F(T)等价.

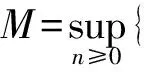
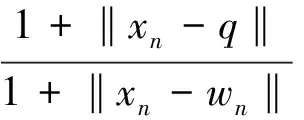
由式(1)，(5)有

(6)

由式(1)，(6)有

(7)

其中ξn=αn(5+2M)+(3+M)(βn+δn)+(M+1)(γn+μn)→0(n→∞).

由于T：D→D是依中间意义渐近非扩张的，记dn=max{0，supx,y∈D(‖Tnx-Tny‖-‖x-y‖)}，则dn→0(n→∞)，从而由式(7)，(8)有

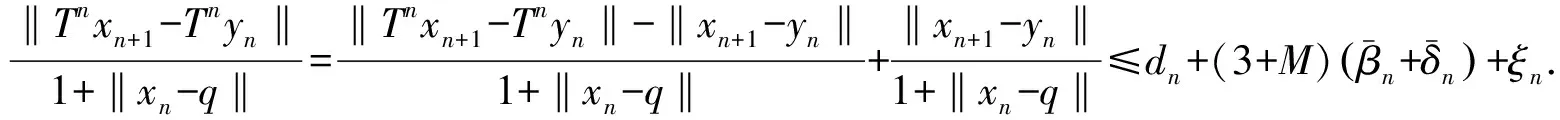
类似地，

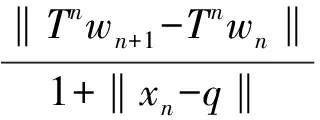
于是

(9)

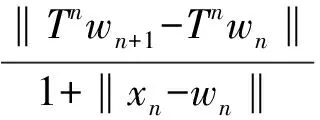
(10)

由式(1)和引理1知，存在j(xn+1-wn+1)∈J(xn+1-wn+1)，使

现在考虑式(11)右端各项.右端第二项，使用式(3)有

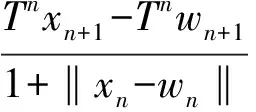
(12)

其中fn={〈Tnxn+1-Tnwn+1,j(xn+1-wn+1)〉-kn‖xn+1-wn+1‖2+φ(‖xn+1-wn+1‖)}.右端第三项，使用式(4)，(9)，∀n>n1，有

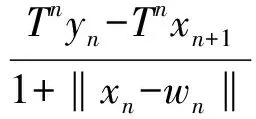
(13)

右端第四项，使用式(4)，(10)，∀n>n1，有

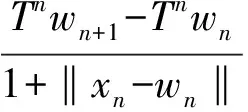
(14)

其中ηn=dn+3αn+G(γn+μn)→0(n→∞).

将式(12)，(13)和(14)代入式(11)得

(15)

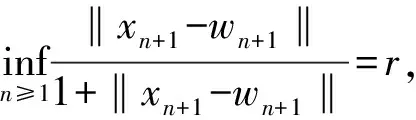
其中B=max{‖x1-w1‖,‖x2-w2‖,…,‖xN-wN‖}.下面证明∀j≥1，有‖xN+j-wN+j‖<2B.当j=1时，由式(15)有

‖xN+1-wN+1‖2≤ ‖xN-wN‖2+4αN[4G((2B)2+1)(ξN+dN+ηN)+

因此由归纳法可证∀j≥1，有

即‖xN+j-wN+j‖<2B，从而∀n≥1，‖xn-wn‖≤2B.于是由式(15),∀n≥N，有

‖xn+1-wn+1‖2≤ ‖xn-wn‖2+4αn[4G((2B)2+1)(ξn+dn+ηn)+

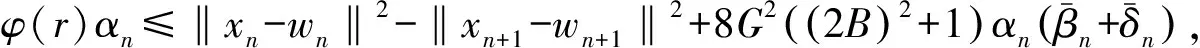
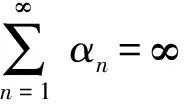
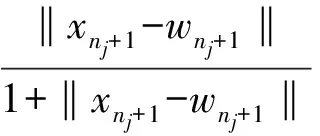
(16)

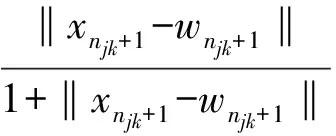
(17)

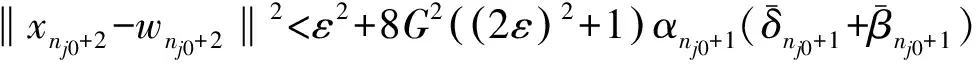
‖xnj0+2-wnj0+2‖2≤‖xnj0+1-wnj0+1‖2+

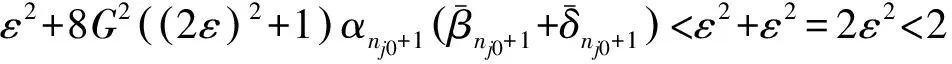
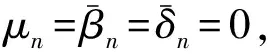
[1] 张石生．Banach空间中Ishikawa迭代序列的稳定性和收敛性问题[J]．数学学报，2007，50(5)：1051-1062．

[2] 张树义，宋晓光．关于修正的Ishikawa迭代序列的稳定性和收敛性[J]．沈阳师范大学学报(自然科学版)，2012，30(4)：449-453．

[3] 张树义，刘冬红，李丹．k-次增生算子方程的迭代解[J]．北华大学学报(自然科学版)，2015，16(5)：574-578．

[4] 赵美娜，张树义，赵亚莉．Banach空间中k-次增生算子方程解的迭代逼近[J]．北华大学学报(自然科学版)，2015，16(6)：720-724．

[5] 张树义，宋晓光，万美玲，等．非Lipschitz渐近伪压缩映象不动点的迭代逼近[J]．北华大学学报(自然科学版)，2014，15(5)：581-587．

[6] 张树义，万美玲，李丹．渐近伪压缩型映象迭代序列的强收敛定理[J]．江南大学学报(自然科学版)，2014，13(6)：726-730．

[7] 张树义，赵美娜，李丹．渐近半压缩映象具混合型误差的迭代收敛性[J]．北华大学学报(自然科学版)，2015，16(3)：281-285．

[8] 万美玲，张树义，郑晓迪．赋范线性空间中φ-强增生算子方程解的迭代收敛性[J]．北华大学学报(自然科学版)，2016，17(3)：305-307．

[9] 谷峰．两个有限族一致L-Lipschitz映象的平行迭代算法的强收敛定理[J]．数学学报，2010，53(6)：1209-1216．

[10] 张树义，林媛．Φ-φ-型压缩映象不动点的存在性[J]．北华大学学报(自然科学版)，2016，17(1)：1-3．

[11] 张树义，赵美娜，刘冬红．弱相容映射的几个新的公共不动点定理[J]．江南大学学报(自然科学版)，2015，14(6)：852-856．

[12] 张树义，宋晓光，栾丹．Φ-压缩映象的公共不动点定理[J]．北华大学学报(自然科学版)，2014，15(2)：167-173．

[13] 张树义，赵美娜，李丹．关于平方型Altman映象的公共不动点定理[J]．江南大学学报(自然科学版)，2015，14(4)：472-477．

[14] 张树义．赋范线性空间中渐近拟伪压缩型映象不动点的修改的广义Ishikawa迭代逼近[J]．应用数学学报，2011，34(5)：886-894．

[15] 张树义．一致Lipschitz渐近φi-型拟伪压缩映象多步平行迭代算法的收敛性[J]．系统科学与数学，2013，33(10)：1233-1242．

[16] 宣渭峰，王元恒．双复合修正的Ishikawa迭代逼近非扩张映像不动点[J]．浙江师范大学学报(自然科学版)，2009，32(4)：401-405．

[17] 张树义，衣立红，邵颖．Altman型映象的公共不动点[J]．杭州师范大学学报(自然科学版)，2008，7(6)：401-404．

TheEquivalenceofConvergenceofIterativeSequencesforAsymptoticallyPseudocontractiveMappings

ZHAO Meina1, ZHANG Shuyi1, JIN Heng2

(1. College of Mathematics and Physics， Bohai University， Jinzhou 121013， China;2. College of Mathematics Sciences， Inner Mongolia Normal University， Hohhot 010022， China)

The equivalence of the convergence of modified Ishikawa and modified Mann iterative sequences with mixed errors for asymptotically nonexpanisive mappings in the intermediate sense and asymptotically pseudocontractive mappings in Banach spaces is studied without any bounded assumption, the results presented in this paper extend and improve the corresponding results in some references.

real Banach space; asymptotically pseudocontractive mapping; asymptotically nonexpanisive mappings in the intermediate sense; modified Ishikawa iterative sequences with mixed errors; modified Mann iterative sequence with mixed errors

2016-06-22

国家自然科学基金项目(11371070).

张树义(1960-)，男，教授，主要从事非线性泛函分析及应用研究.E-mail:jzzhangshuyi@126.com

10.3969/j.issn.1674-232X.2017.06.015

O177.91MSC201047H06；47H10；47H17

A

1674-232X(2017)06-0653-06