基于模糊层次熵的实战化教学质量评价方法∗

李 磊 牛晓博

（海军士官学校 蚌埠 233012）

基于模糊层次熵的实战化教学质量评价方法∗

李 磊 牛晓博

（海军士官学校 蚌埠 233012）

分析了建立实战化教学质量评价体系的必要性，建立了实战化教学质量评价指标体系。针对该评价指标体系及以往评价方法存在的问题，提出了基于模糊层次熵（F&E-AHP）的实战化教学质量评价方法，该方法将三角模糊数引入层次分析法，并结合专家打分情况动态调整权值，通过实例证明了该方法的有效性。

模糊层次熵；实战化教学；评价指标体系；量化评估

1 引言

随着实战化教学的不断深入，评价教学质量的传统方法，如督导专家按指标打分，学员网上测评等，越发显得不够精细、不能体现实战化教学质量情况。专家督导不能精确把握授课内容与岗位吻合情况，学员测评不能从宏观上把握教学目的、方式方法，同行督导侧重知识内容、岗位技能，缺乏全校性的统一标准。因此针对实战化教学，需要从宏观教学规律出发，立足部队岗位技能，结合学员学习效果，制定一套反映实战化教学的新指标以及更加精细的评估方法。

2 实战化教学质量评价指标体系

军队院校实战化教学不同于地方院校教学，它担负着培养上岗顶用人才的使命。因此，对军队院校实战化教学进行评价，在遵循宏观教学规律的同时，要有自己相对独立的指标体系。借鉴地方高校教学评价体系，结合军队院校实际情况，按照军队院校教学使命地位，以培养贴近岗位、部队顶用人才为目标，参照军队院校教学工作评价指标体系，建立了军队院校实战化教学评价指标体系。体系见表1。

本指标体系将对军队院校实战化教学产生影响的各因素进行了汇总，按照每个因素自身的特点进行分析，合理分组、统筹安排。由抽象到具体，由总体到部分逐级分析，逐级细化。共产生了3个一级指标，10个二级指标，31个评价点，基本涵盖了军队院校实战化教学的各个方面。

表1 实战化教学质量评价指标体系［1～3］

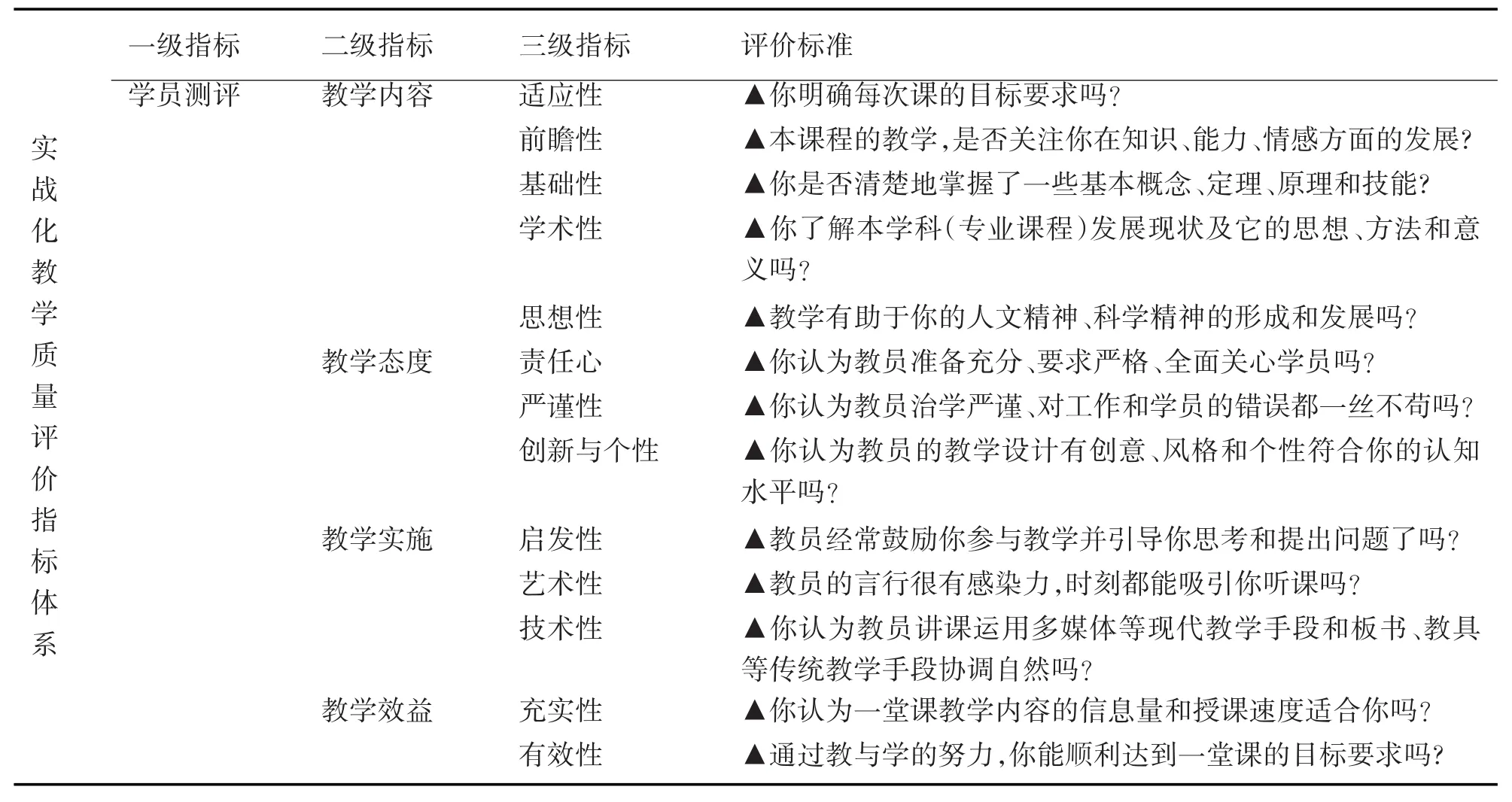
续表1

3 模糊层次熵在实战化教学质量评价中的应用

建立了复杂的实战化教学质量评价指标体系，如果没有针对该体系的评价方法，只是采用各个评价点单独打分的方法不能反映出实战化教学质量的总体情况，更会使专家陷入大量的数据中，影响决策分析。因此，需要一种合理的评价方法，将专家对各个评价点的打分情况进行汇总，最终得到一个对实战化教学质量的总体评价或量化指标。

以往进行指标权重的确定需要专家给出一个明确的两两比较的判断矩阵，但是这种方法对专家要求很高，判断矩阵的一致性指标难以达到［4～5］。由于专家偏好不同，并且对评价点重要性的判断本身就存在模糊性，因此要求专家明确给出各评价点孰轻孰重，并给出准确的轻重量化值，显然是不合理的。需要引入一种模糊机制，使专家对评价点的评价在一定误差允许的范围之内，而不要求专家给出明确的判定，可以减轻专家意见的分歧度，利于建立合理有效的评价方法。

采用模糊层次分析法与决策中的熵技术相结合，建立模糊层次熵的多目标评价决策模型。采用模糊层次分析法（F-AHP）确定权系数，并用熵权法对权值进行修正，可以提高权值确定的准确性。

3.1 模糊层次分析法

荷兰学者Van Loargoven提出了用三角模糊数表示比较判断的方法，并运用对三角模糊数的运算和最小二乘法，求得元素的排序，即在模糊环境下使用 AHP的方法［6～7］。

1）建立多级递阶结构模型与模糊判断矩阵

同一层次的元素作为准则对下一层次的某些元素起支配作用，同时又受到上一层次元素的支配。用三角模糊数(l，m，u)定量表示在给定准则下，同一层次各因素间两两比较的结果。l与u表示判断的模糊程度。设q=u-l，q大则模糊程度高；q小则模糊程度低；q=0则判断是非模糊的。

2）三角模糊数学理论及其运算

为进一步计算模糊判断矩阵，引入如下定理。

3）确定层次分析的模糊权重

（1）设 M1，M2是两个模糊数，M1＞M2的可能性程度被定义为V(M1≥M2)：

当 m1≥m2时，

（2）三角模糊数M大于k个三角模糊数Mi(i=1，2，...，k)的可能性程度被定义为

Si表示在给定准则下，同一层次每一个元素同所有元素相比较的综合重要程度值，用Ai表示第i个 元 素 ，设 d′(Ai)=minV(Si≥Sk)(k=1，2，…，m;k≠i) ，那么权重向量为 W′=(d′(A1)，d′(A2)，…，d′(An))T。经归一化处理后，模糊AHP的权重向量为

3.2 基于熵技术改进层次分析法的权重

所谓层次熵权多目标决策分析模型，使用Fuzzy AHP法决定指标的模糊权重，利用决策矩阵提供的信息，进一步用多目标决策中的熵技术修正决策者先前确定的优先权重［8］，再利用模糊综合评判确定最优方案。

熵在信息理论中作为不确定性和信息量的度量。系统的熵是系统有序无序程度的度量，熵越大，系统越无序；反之，则系统越有序。熵权完全利用原始指标数据信息，以指标值之间的差异大小反应指标的“信息价值”来确定权重［9～11］。

m个方案，n个指标的多目标决策问题的决策矩阵D为

其中，xij(i=1，2，...，m;j=2，3，...，m)表示第 i个方案对第 j个指标的数值。

设标准化矩阵为R=(rij)m×n

1）对效益指标：

3.3 模糊层次熵在实战化教学质量评价中的应用

由专家通过对各级指标和评价点重要性程度的模糊判断，通过F-AHP得到各级指标和评价点的权重［12］，然后通过熵权法对权重进行修正。专家对各个评价点单独打分后，按照分析得到的权重对打分进行汇总，可以得到对实战化教学情况的总体得分，从而实现实战化教学情况的定量评价。

不同专家对同一评价点打分时会出现这样的情况：有的评价点专家认同度较高，比如都认为该点打分在90分以上，或都在50分以下，意见一致说明专家判断比较准确地反映了该评价点的真实情况，这种认同度高的指标需要适当加大权重；有的评价点专家意见分歧较大，说明打分专家在该评价点上把握不准，需要在该点上适当减小权重。

因此将式（12）的权值调整公式修改为

采用模糊层次熵进行实战化教学情况评估的流程如图1所示。

4 算例分析

对某次堂课教学进行评估，以学校督导一级指标下，目标效益二级指标的各评价点为例，各评价点的重要性比较采用九标度法，各因子重要性比较标度及含义如表2所示。

表2 九标度各因子重要性大小比较数量化表

专家通过对各评价点重要性比较，给出的模糊判断矩阵如表3所示。

表3 模糊判断矩阵

采用模糊层次分析法计算结果如表4。

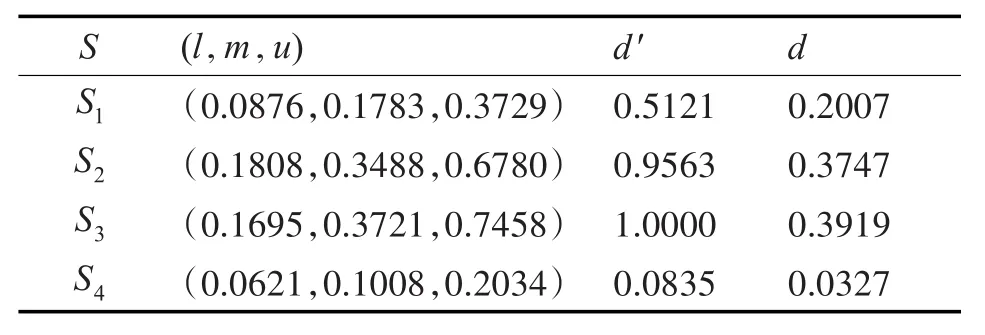
表4 模糊层次分析结果

邀请三位专家给该“目标效益”二级指标下的各评价点依据表5的标准进行打分。

表5 专家打分依据表

专家给出的打分矩阵D：

将专家的评分取平均作为该评价点的得分average(D)=[8 9.3333 82.3333 63.3333 71.6667]

四个指标的熵权分别为λ=[0.0332 0.0151 0.9257 0.0260]

经过信息熵修正后，得到该级指标各评价点相对于“目标效益”二级评价的权重如表6所示。

各级指标计算完后，按照层次分析法对各级指标的合成方法，最终可以得到对该次堂课教学的总评成绩。

5 结语

建立了军队院校实战化教学质量评价指标体系，针对评价指标体系，提出了一种基于模糊层次熵的评价方法，通过算例证明了本算法的有效性。本方法指标分析明确，具有很强的实用性和可操作性，易于编程实现，便于该方法的测试与推广，从而可以极大地提高实战化教学质量评价的科学性和合理性。

［1］王琳.高职教学评价现状分析［J］.职业教育研究，2007，24（12）：58-60.

［2］Wu Lichun.A Study of Practical Teaching Quality Evalua⁃tion System and Weight in Higher Vocational Education［C］//2011 2nd International Conference on Management Science and Engineering Advances in Artificial Intelli⁃gence，2011.

［3］陈宝春.高职实践教学评价指标体系的构建［J］.高等函授学报，2010，23（1）：26-28.

［4］汪应洛.系统工程理论、方法与应用［M］.北京：高等教育出版社，1998.

［5］Charnes A，Cooper W W，Rhodes E.Measuring the effi⁃ciency of decision making units［J］.European Journal of Operation Research，1978，（2）：429-444.

［6］龚艳冰，陈森发.三角模糊数互补判断矩阵的一种排序方法［J］.模糊系统与数学，2008，22（1）：127-131.

［7］Lipovetsky S.et al.Robust estimation of priorities in the AHP［J］.European Journal of Operational Research，2002，137：110-122.

［8］罗进.利用信息熵计算评价指标权重原理及实例［J］.武汉纺织大学学报，2014，27（6）：27-31.

［9］曹连英，杨秀菊.基于信息熵的教学质量可度量化研究［J］.哈尔滨师范大学自然科学学报，2008，24（2）：64-66.

［10］曾三云，龙君.基于信息熵的模糊多属性决策方法［J］.广西科学，2008，15（2）：135-137.

［11］洪航，商靠定，张学魁等.基于信息熵评价决策模型的突发公共事件应急处置指挥方案优选［J］.中国安全科学学报，2009，19（2）：160-164.

［12］於实.模糊层次分析法在教学质量评价中的应用研究［J］.计算机仿真，2012，12（6）：369-372.

An Assessment Arithmetic of Combat-oriented Education Based on F&E-AHP

LI LeiNIU Xiaobo
（Naval Petty Officer Academy，Bengbu 233012）

An assessment index architecture of combat-oriented education is established based on the importance analyzing of this architecture.A Fuzzy&Entropy-AHP（F&E-AHP）quantitative assessment arithmetic is applied aiming at the assessment in⁃dex architecture and the limitations in the earlier assessment arithmetices.This arithmetic combines the fuzzy trigonometric function with AHP，and can adjust the weight of each index consulting the expert scoring dynamicly.The validity of this technology is proved through an example.

Fuzzy&Entropy-AHP， combat-oriented education， assessment index architecture， quantitative assessment

TP391

10.3969/j.issn.1672-9730.2017.11.027

Class Number TP391

2017年5月7日，

2017年6月12日

李磊，男，硕士，讲师，研究方向：职业技术教育，通信系统。牛晓博，男，硕士，讲师，研究方向：模式识别与智能系统，职业技术教育。