黑龙江省春季低温指数小波分析

田宝星，宫丽娟，杨 帆，李浩然，季生太，于 敏

（1.黑龙江省气象科学研究所，哈尔滨150030；2.黑龙江省气象局机关服务中心，哈尔滨150030；2.东北农业大学 资源与环境学院，哈尔滨150030）

黑龙江省春季低温指数小波分析

田宝星1，宫丽娟1，杨 帆2，李浩然3，季生太1，于 敏1

（1.黑龙江省气象科学研究所，哈尔滨150030；2.黑龙江省气象局机关服务中心，哈尔滨150030；2.东北农业大学 资源与环境学院，哈尔滨150030）

通过黑龙江省1971—2014年春季最低气温资料，结合低温指数模型，利用趋势分析和Morlet小波函数，研究了黑龙江省近44年来的春季低温指数变化趋势，揭示了该地区春季低温指数的多时间尺度的周期性变化。结果表明：黑龙江省春季低温指数呈现减少趋势，1980s以来气温明显增加，春季低温指数明显减少，而2010s春季低温指数明显增加，与极端气温的升高有关。春季低温指数存在3个尺度的周期变化，分别是17～29 a，7～16 a和3～6 a。17～29 a和7～16 a尺度非常稳定，具有全域性。4～14 a尺度在1990s后期较为稳定。10～15 a尺度周期变化最明显。11～15 a尺度能量最强且周期最显著；10～18 a尺度能量几乎贯穿整个时域；19～26 a尺度占据整个研究时域大部分。其中春季低温指数具有20 a，12 a，6 a和2 a左右的主周期，其中12 a尺度为第一主周期，平均周期为8.5 a。

低温；春季；小波分析；黑龙江省

近百年来，地球气候正经历着一次以全球变暖为主要特征的显著变化[1]，使得灾害性天气频发，造成生态和环境恶化，严重影响到农业生产、社会经济和可持续发展，已引起人们的高度重视。黑龙江省是全国重要的粮食生产基地之一，每年向国家输出的粮食总产量居全国首位[2]，对保障国家粮食安全至关重要。21世纪以来，受气候变化影响，黑龙江省春季低温事件频繁发生，2009—2014年黑龙江省不同区域、不同时间均发生了不同程度的阶段性低温，对粮食产量和品质造成巨大的影响，导致玉米籽粒含水率高，加大捂霉风险；水稻形成障碍型冷害，使产量下降。春季（1年中，从冬季到夏季之间的季节，气象上指每年3月到5月一段时期[3]）是作物生产最关键环节，适时播种能够争取充足热量，是获得高产的基本前提，但低温往往导致作物迟播。研究春季低温指数的变化规律，对科学搭配种植作物品种，保障粮食安全具有重要的意义。

小波分析方法是一种信号时频局部分析的新方法，其特点是通过时频变化突出信号在某些方面的特征，具有时频多分辨功能[4]。它在傅里叶变换的基础上引入窗口函数，把时间序列分解为时间和频率的贡献[5]；在不同时间尺度上分析气候的变化趋势，解释气候变化的多尺度构成和主周期及气候变化多尺度结构和突变特征等方面具有明显的优势[6-7]，已成为热量资源多时间尺度变化特征的有效分析手段[8-9]。

本文利用黑龙江省1971—2014年的完整序列的逐日最低气温资料结合低温指数模型进行趋势检验，然后采用Morlet小波变换分析方法，分析春季低温指数时间序列变化特征和多时间尺度的复杂结构，对该区域合理规划农业生产布局具有重要的指导意义。

1 材料与方法

1.1 研究区概况

黑龙江省属于寒温带与温带大陆性季风气候。全省从南向北，依温度指标可分为中温带和寒温带；从东向西，依干燥度指标可分为湿润区、半湿润区和半干旱区。全省气候的主要特征是春季低温干旱，夏季温热多雨，秋季易涝早霜，冬季寒冷漫长，无霜期短，气候地域性差异大。全省年平均气温多在-5～5℃，大致以嫩江、伊春一线为0℃等值线[10]。

1.2 材料来源

选取黑龙江省80个气象站点逐日最低气温资料，材料来自于黑龙江省气象信息中心。连续不超过5 d的缺测资料采用线性内插法进行插补，超过5 d的缺测记录用线性回归法进行插补。小波分析方法具有多种模式，本文采用Morlet变换分析。计算过程在Matlab软件平台下，通过编写数据处理程序，计算小波系数，并绘制实部值、模部平方值图像以及小波方差图像。

1.3 研究方法

1.3.1 低温指数 低温指数[11]定义为一年中（或某一时段）至少5 d最低温度低于多年日最低温度平均值5℃的总日数。假定Tij为第j年第i天的日最低温度，Ti，平均为第i天1971—2014年日最低温度平均值。则低温指数为某段时间至少5 d的Tij＜Ti，平均-5℃的总日数。

1.3.2 趋势性分析 趋势分析法[12-13]，又称为比较分析法，它是将连续的两期或多期相同指标或比率进行定基对比和还比对比后得出它们的增减变动方向、数额和幅度，用以揭示变化趋势。通常气候要素时间变化趋势的描述采用一元一次线性方程，即：

式中：t表示年序；a表示线性方程的斜率，即气候要素的线性变化趋势与速率。当a＞0时表示增加趋势，当a＜0时表示减少趋势，当a=0时则表示无变化趋势，且将a×10定义为气候倾向率，b为常数，可采用最小二乘法求出。

1.3.3 小波分析

（1）小波函数。小波分析[14-15]的基本思想是用一簇小波函数系来表示或逼近某一信号或函数。因此，小波函数是小波分析的关键，它是具有震荡性、能够迅速衰减到0的一类函数，即小波函数Ψ（t）∈L2（R）且满足：

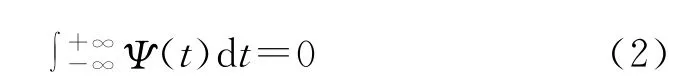
式中：Ψ（t）为基小波函数，它可通过尺度的伸缩和时间上的平移构成一簇函数系：

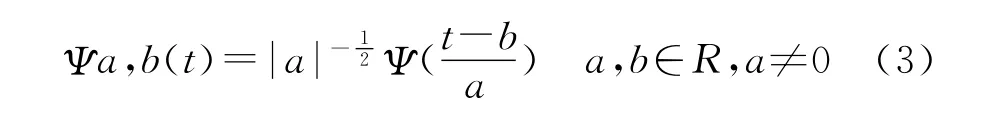
式中：Ψa，b（t）为子小波；a为尺度因子，反映小波的周期长度；b为平移因子，反映时间上的平移。

（2）小波变换。若Ψa，b（t）是由公式（2）给出的子小波，对于给定的能量有限信号f（t）∈L2（R），其连续小波变化（Continue Wavelet Transform，简写为CWT）为：

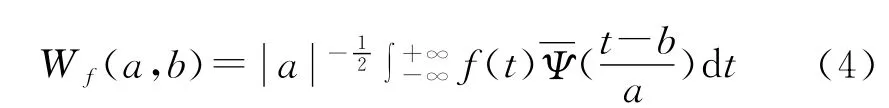
式中：Wf（a，b）为小波变换系数；f（t）为一个信号或平方可积函数；a为伸缩尺度；b为平移参数。地学中观测到的时间序列数据大多是离散的，设函数f（kΔt），k=1，2，…，N；Δt为取样间隔，则公式（4）的离散小波变换形式为：

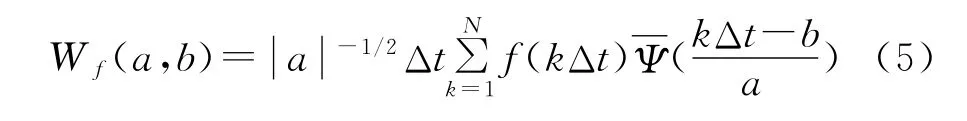
由公式（4），（5）可知小波分析的基本原理，即通过增加或减小伸缩尺度a来得到信号的低频或高频信息，然后分析信号的概貌或细节，实现对信号不同时间尺度和空间局部特征的分析。

（3）小波方差。将小波系数的平方值在b域上积分，就可以得到小波方差，即：

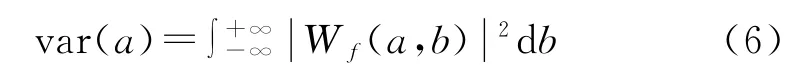
小波方差随尺度a的变化过程，称为小波方差图。由公式（6）可知，它能反映信号波动的能量随尺度a的分布。因此，小波方差图可用来确定信号中不同种尺度扰动的相对强度和存在的主要时间尺度，即主周期。

2 结果与分析

2.1 春季低温指数的趋势性分析

由图1可见，研究区域1971—2014年春季平均低温指数呈现下降趋势，从趋势线来看，春季低温指数每10 a降低1.16 d。近44年来春季平均低温指数为5 d，最大值出现在1980年，为19 d；最小值出现在2002年，为0 d，最大值和最小值差值明显，说明黑龙江省春季升温明显，与王秀芬[16]和陈晶[17]等关于黑龙江省气温季节变化研究一致，以至于春季低温持续天数明显减少。该区春季低温指数年代际变化表现明显，从20世纪80年代以来气温增加明显[18]，春季低温指数从20世纪70年代的7.80 d减少到80年代的7.25 d，20世纪90年代和21世纪初，春季低温指数较低在2～3 d左右，而21世纪10年代以来春季低温指数又明显增加，与极端气温的升高相一致。

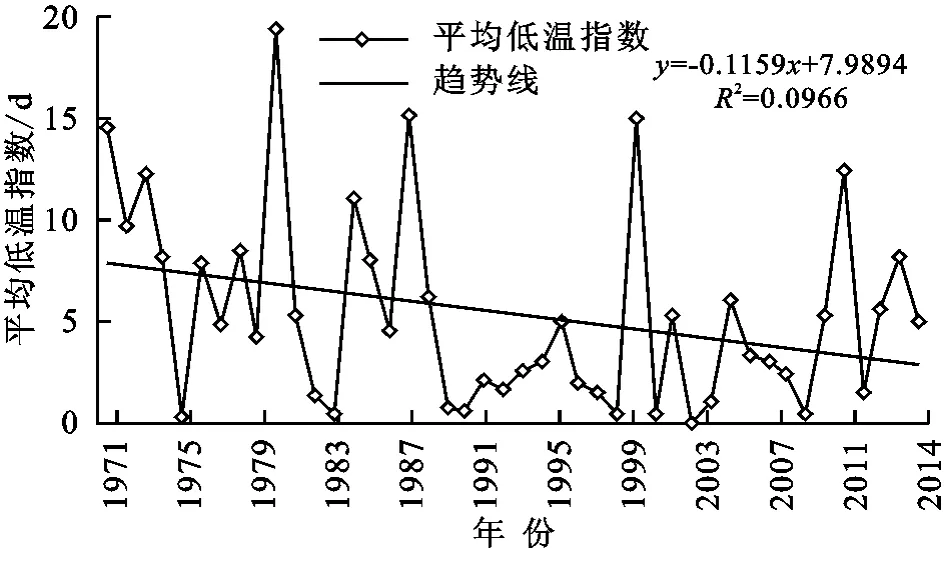
图1 黑龙江省1971-2014年春季平均低温指数变化趋势

2.2 春季低温指数的小波分析

由图2中，实线表示正相位，即实部大于等于0；虚线表示负相位，即实部小于0，图中清晰地显示了小波变换系数的实部的波动特征，具体反映在该区春季低温指数偏多和偏少交替变化的特性，可以清楚地看到黑龙江省春季低温指数演化过程中存在的多时间尺度特征。总的来说，在春季低温指数演变过程中存在着17～29 a，7～16 a和3～6 a的3类尺度的周期变化规律。其中，在17～29 a尺度上出现了低—高交替的准两次震荡；在7～16 a时间尺度上存在准4次震荡。同时，还可以看出以上两个尺度的周期变化在整个分析时段表现地非常稳定，具有全域性；而4～14 a尺度的周期变化，在1990s中期后表现的较为稳定。

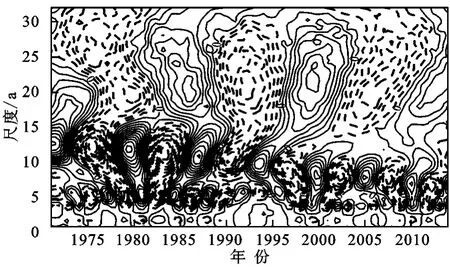
图2 黑龙江省春季低温指数小波系数实部等值线

Morlet小波系数的模值是不同时间尺度变化周期所对应的能量密度在时间域中分布的反映，系数模值愈大，表明其所对应时段或尺度的周期性就愈强。从图3可以看出，在春季低温指数演化过程中，10～15 a时间尺度模值最大，说明该时间尺度周期变化最明显，在20～25 a时间尺度的周期变化次之，其他时间尺度的周期性变化较小。

图3 黑龙江省春季低温指数小波系数模等值线

小波系数的模方相当于小波能量谱，它可以分析出不同周期的震荡能量。由图4可知，11～15 a时间尺度的能量最强、周期最显著，10～18 a时间尺度的能量次之，但几乎贯穿整个时域；19～26 a时间尺度能量虽然较弱，但周期分布比较明显，占据整个研究时域大部分（1980—2005年）。

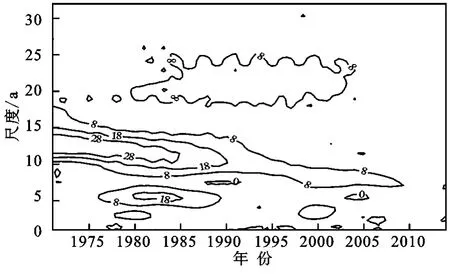
图4 黑龙江省春季低温指数小波系数模方等值线

春季低温指数的小波方差图中（图5）存在4个较为明显的峰值，它们依次对应着20 a，12 a，6 a和2 a的时间尺度。其中，最大峰值对应着12 a的时间尺度，说明12 a左右的周期震荡最强，为春季低温指数变化的第一主周期；20 a时间尺度对应着第二峰值，为春季低温指数变化的第二主周期，第三、第四峰值分别对应着6 a和2 a的时间尺度，它们依次为春季低温指数的第三和第四主周期。这说明上述4个周期的波动控制着春季低温指数在整个时间域内的变化特征。

根据小波方差检验的结果，绘制了春季低温指数演变的第一和第二主周期小波系数图（图6）。从主周期趋势图中我们可以分析出在不同的时间尺度下，春季低温指数的平均周期及低—高变化特征。图6A显示，在12 a特征时间尺度上，春季低温指数的平均周期为8.5 a左右，大约经历了5个低—高转换期；而在20 a特征时间尺度上（图6B），春季低温指数的平均变化周期为11 a左右，大约4个周期的低—高变化。

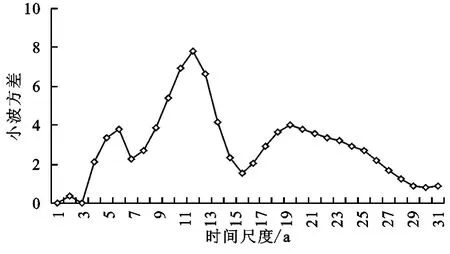
图5 黑龙江省春季低温指数小波方差

图6 黑龙江省春季低温指数的12 a,20 a特征时间尺度小波实部过程线

3 结论

（1）黑龙江省1971—2014年春季平均低温指数呈现下降趋势，变率为每10 a降低1.16 d，说明黑龙江省春季升温明显。年代际变化明显，研究表明20世纪80年代以来气温增加明显，在20世纪末期至21世纪初期春季低温指数最低，表明这个时期也是最温暖的时期。21世纪10年代春季低温指数又明显增加，与极端气温的升高有关。

（2）通过对黑龙江省春季低温指数的小波分析，得出黑龙江省春季低温指数主要存在17～29 a，7～16 a和3～6 a的3类尺度的周期变化规律。17～29 a尺度和7～16 a尺度，在整个时段表现的非常稳定，具有全域性。4～14 a尺度在1990s中期后较为稳定。

（3）不同时间尺度下，小波系数模值反映其对应时段或尺度的周期性强弱。春季低温指数10～15 a尺度模值最大，该尺度周期变化最明显，20～25 a尺度模值次之。

（4）小波系数模方可以分析不同尺度的震荡能量。11～15 a尺度的能量最强、周期最显著，10～18 a尺度几乎贯穿整个时域；19～26 a尺度能量虽然较弱，占据整个研究时域大部分（1980—2005年）。

（5）小波方差图中，黑龙江省春季低温指数序列具有20 a、12 a、6 a和2 a的时间尺度主周期，其中12 a左右的时间尺度周期震荡最强，为第一主周期；20 a左右的时间尺度为第二主周期。

（6）春季低温指数的第一和第二主周期小波系数，在12 a和20 a特征时间尺度上，平均周期为分别为8.5 a和11 a左右。

[1]秦大河，陈振林，罗勇，等.气候变化科学的最新认知[J].气候变化研究进展，2007，3（2）：63-73.

[2]姜丽霞，王晾晾，杜春英，等.1971—2014年黑龙江省春季气温演变特征及对作物播种期的影响[J].资源科学，2015，37（4）：849-857.

[3]中国气象影视信息网.气象术语[EB/OL].（2013-08-20）[2016-02-14]http：∥www.qxkp.net/xxyd/qxsy/335795.shtml.

[4]王文圣，丁晶，李跃清.水文小波分析[M].北京：化学工业出版社，2005.

[5]姜晓艳，刘树华，马明敏，等.东北地区近百年降水时间序列变化规律的小波分析[J].地理研究，2009，28（2）：354-362.

[6]刘晓梅，闵锦忠，刘天龙.新疆叶尔羌河流域温度与降水序列的小波分析[J].中国沙漠，2009，29（3）：566-571.

[7]张军涛，李哲，郑度.温度与降水变化的小波分析及其环境效应解释：以东北农牧交错区为例[J].地理研究，2002，21（1）：54-60.

[8]覃军，张录军，胡江林.武汉近百年来气温变化的多时间尺度分析[J].气象科学，2001，21（2）：206-210.

[9]尤卫红，段旭，杞明辉.连续小波变换在云南近百年气温和降水变化分析中的应用[J].高原气象，1999，18（1）：47-54.

[10]李瑶，于宗辰，高璐迪，等.黑龙江省近50 a农业界限温度变化特征分析[J].黑龙江气象，2015，32（2）：16-18.

[11]王艳华，任传友，黄瑞冬，等.中国近45年低温指数时空持续变化分析[J].自然灾害学报，2013，22（2）：116-123.

[12]施能，陈家其，屠其璞.中国近100年来4个年代际的气候变化特征[J].气象学报，1995，53（4）：431-439.

[13]曹萌萌.气候变暖背景下黑龙江省水稻种植适宜性区划[D].哈尔滨：东北农业大学，2014.

[14]李淼，夏军，陈社明，等.北京地区近300年降水变化的小波分析[J].自然资源学报，2011，26（6）：1001-1011.

[15]潘雅婧，王仰麟，彭建，等.基于小波与R/S方法的汉江中下游流域降水量时间序列分析[J].地理研究，2012，31（5）：811-820.

[16]王秀芬，杨艳昭，尤飞.近30年来黑龙江省气候变化特征分析[J].中国农业气象，2011，32（S1）：28-32.

[17]陈晶，杨帆，田宝星，等.黑龙江省黑土区近50年来四季气温时空变化特征分析[J].水土保持研究，2013，20（3）：150-154.

[18]张立友，陈晶，李维海，等.近50年黑龙江省黑土区气温时空变化特征分析[J].东北农业大学学报，2014，45（2）：48-53.

Wavelet Analysis on Lowest Temperature Index in Spring in Heilongjiang Province

TIAN Baoxing1，GONG Lijuan1，YANG Fan2，LI Haoran3，JI Shengtai1，YU Min1
（1.Heilongjiang Province Institute of Meteorological Science，Harbin150030，China；2.Heilongjiang Meteorological Bureau In-house Service Centre，Harbin150030，China；3.College of Resources and Environment，Northeast Agricultural University，Harbin150030，China）

Based on the owest temperature index model and the lowest temperature data of Heilongjiang Province in spring from 1971 to 2014，trend prediction and Morlet wavelet were used to examine the change trend and periodic change of multiple time scale to the lowest temperature index of spring in Heilongjiang Province during the past 44 years.The results showed that it was a downtrend to the lowest temperature index of spring in Heilongjiang Province.The lowest temperature index of spring had significantly decreased as the temperature had increased obviously since 1980s.However，the lowest temperature index of spring significantly increased with the rise of extreme temperature in 2010s.There were 3 periodic changes of scales in the lowest temperature of spring，which were 17～29 years，7～16 years，and 3～6 years.The scales of 17～29 years and 7～16 years were very stable in the whole duration.The scale of 4～14 years was more stable in the later of 1990s.The scale of 10～15 years was the most obvious.The scale of 11～15 years was the strongest energy and most significantly cycle.The energy of 10～18 years was almost throughout the whole duration.The scale of 19～26 years occupied in the most of whole duration.The main cycle of the lowest temperature index of spring had 20 years，12 years，6 years，2 years，the scale of 12 years was the first main cycle，and the average cycle was about 8.5 years.

low temperature；spring；wavelet analysis；Heilongjiang Province

P49

A

1005-3409（2017）01-0342-04

2016-01-06

2016-02-14

气象关键技术集成与应用项目（CMAGJ2015M18）；黑龙江省气象局科学技术研究（HQJJ2015018，HQ2016015）

田宝星（1986—），男，黑龙江哈尔滨人，助理工程师，硕士，主要从事应用气象和气候资源研究。E-mail：bx-tian＠163.com

于敏（1975—），女，黑龙江哈尔滨人，高级工程师，博士，主要从事大气遥感与大气环境及应用气象研究。E-mail：yy629＠sina.com