基于NSCT的多模态医学图像融合算法的研究

徐磊，曹艳

南京医科大学附属南京医院（南京市第一医院） 核医学科，江苏 南京 210006

基于NSCT的多模态医学图像融合算法的研究

徐磊，曹艳

南京医科大学附属南京医院（南京市第一医院） 核医学科，江苏 南京 210006

目的提出一种新颖的非下采样轮廓波变换算法，并将其用于多模态医学图像融合领域。方法第一步，采用非下采样轮廓波变换将源图像分解为高频和低频子图像；第二步，低频部分采用区域均值取大融合规则，能保留图像的绝大部分信息，获得更高的对比度和清晰度，高频图像采用取大区域方差取大融合原则，能有效地突出图像细节信息；第三步，采用非下采样轮廓波逆变换将融合子图像进行重构运算，获得最终的融合图像。结果6组医学图像融合实验表明，基于本文提出算法获得的融合图像质量最佳，且定量评价指标熵、平均值、标准差、边缘强度分别较其他算法提升0～40%、3%～42%、1%～42%和0.4%～48%。结论基于本文提出的算法融合效果优越，具有较高普适性和实用性，是一种可行的、有效的医学图像融合算法。

非下采样轮廓波变换；多模态图像融合；融合规则；医学影像

引言

随着医学影像设备学、计算机技术和生物医学工程的迅速发展，医学影像设备提供了多种模态的医学图像[1]。由于各模态影像设备成像原理不同，单一模态医学图像包含的信息有限，且不同模态图像之间存在互补和冗余，其中MRI、CT、USG和MRA能提供高分辨率的解剖图像，而PET、SPECT和fMRI提供低分辨率的功能图像。怎样将解剖与功能成像结合在一起以便获得对同一目标更有用、更精确的信息，多模态医学图像融合技术是目前唯一一种能将多种图像的相关互补信息结合在一幅图像上的方法，被广泛应用于临床诊断、外科手术、放疗等方面[2]。

多年来国内外在图像融合领域的研究成果表明[3-4]，图像融合技术可分为3类：像素级融合、特征级融合和决策级融合。由于像素级融合直接作用于图像像素空间，容易实施，运算效率高，且能提供更丰富可靠的信息，是目前最常用的融合算法。最简单的像素级融合算法是像素灰度平均法[5]，此法直接在图像像素空间上进行融合，融合图像对比度较差；主成分分析法（PCA）、独立成分分析法（ICA）、IHS变换法等方法的融合性能有所提升，但均存在光谱退化的不足[6]；高斯金字塔、拉普拉斯金字塔、形态学金字塔等方法的融合效果受块效应影响较大[7]；离散小波变换近阶段开始兴起，但融合过程容易产生奇异点，且捕捉各方向信息的能力有限[8]；轮廓波变换能给出图像轮廓的渐近最优表示，但上下采用轮廓波变换具有移变性，且容易产生伪吉布斯现象[9]；非下采样轮廓波变换（Non-Sampled Contourlet Transform，NSCT）继承了轮廓波变换的优势[10]，具有移不变性和冗余性，能有效地抑制伪吉布斯现象，使得NSCT方法成为一种高效可行的图像融合算法。

本文主要研究像素级水平上的图像融合，方法是基于非下采样轮廓波变换的改进算法，构建了低频区域均值取大、高频区域方差取大相结合的融合规则，并对融合图像进行一致性检验。

1 方法

1.1 非下采样轮廓波变换理论

NSCT早由Cunha提出，是一种基于轮廓波变换的理论，在几何变换和图像处理方面均取得很好的效果[11]。由于在拉普拉斯金字塔和方向滤波器组中使用上采样和下采样，轮廓波变换不可避免带有移变性，然而非下采样轮廓波变换具有移不变、多尺度和多方向等性质，主要由非下采样金字塔滤波器组（Non-Subsampled Pyramid Filter Bank，NSPFB）和非下采样方向滤波器组（Non-Subsampled Directional Filter Bank，NSDFB）组成（图1）。图1很好地解释了非下采样轮廓波变换的分解，其中NSCT的多尺度特性由两个非下采样金字塔滤波器组保证，一次NSCT分解可获得一个低频子图像和一个高频子图像，然后在NSPFB分解水平上，低频部分可以进一步分解捕捉图像的奇异点，分解层数为L时，可获得一幅低频子图像和L幅高频子图像，高低频子带图像尺寸均与源图像大小相同[12-13]。

图1 基于NSCT的图像分解

非下采样方向滤波器组保证了NSCT的多方向性，可以提供图像更多的方向信息，且可以避免使用滤波器中上采样和下采样的操作。NSDFB可对高频子图像进行k层分解，得到与源图像尺寸相同的2k个方向子图像。

1.2 非下采样轮廓波变换的图像融合过程

NSCT是一种快速多尺度的图像融合方法，有着特征区域、多分辨率分解、边缘检测、能量压缩等优势[14]。基于NSCT的图像融合过程，见图2。

图2 基于NSCT的图像融合过程

具体图像融合的一般过程如下：① 选择高度配准的图像作为源图像；② 采用NSCT进行源图像分解，获得各尺度和方向的高低频子带系数；③ 采用高低频融合规则对高低频子图像进行融合处理；④ 将融合后的子图像进行NSCT逆变换即得融合图像。

2 本文提出的融合算法

本文提出的NSCT融合流程，见图3。以CT与MRI融合为例，多模态医学图像在融合之前需要进行预处理，主要包括图像配准、图像尺寸调整和滤波。

不同模态医学图像描述的目标对象在空间上并不一一对应，图像配准可校准同一目标的空间位置[15]；不同设备采集的图像尺寸大小并不相同，需要采用插值法归一化图像尺寸大小[16]；由于中值滤波器能降低多种噪声，且保存图像边缘，因此采用中值滤波器对源图像进行滤波处理。

图3 以CT和MRI融合为例展示本文提出的融合算法流程

2.1 低频系数融合规则

低频子带系数代表图像的主体信息，本文采用邻域平均值取大获得融合低频系数，可以有效地提高融合图像对比度和亮度。首先计算各低频子图像3×3邻域内灰度平均值，然后取较大值作为低频融合系数。如公式(1)和(2)所示，μ(p)表示子图像中以（m，n）为中心的邻域低频系数平均值，，，分别表示源图像A、B和融合图像F在K层NSCT分解的系数。

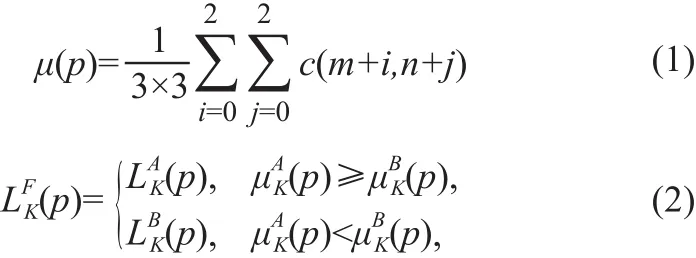
2.2 高频系数融合规则

融合图像中应包含源图像中所有的有用信息，这些有用信息表现为图像的边缘、线条和边界，由高频子带系数表示。由于NSCT分解后的3个高频具有一定的方向性，分为代表水平、垂直和对角线方向的细节部分，在同一分解尺度上，3个高频子带中对应位置的系数大小不等，图像的细节部分主要集中在方向大的高频系数上。因此，本文采用区域方差取大的融合规则，既能考虑邻域内像素之间的关联性，也最大限度的保留源图像的细节部分，保证图像的清晰度。公式如下：

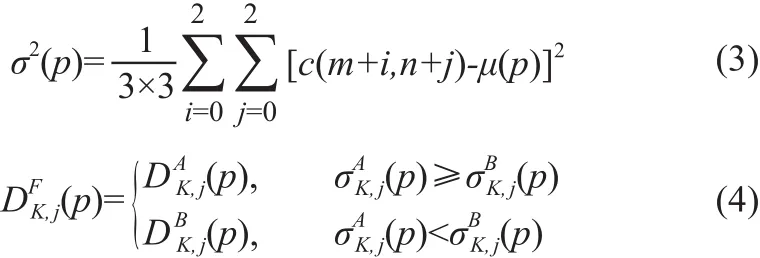
2.3 图像的一致性检验

图像一致性检验是基于图像区域“多数”原则进行的[17]。当融合子图像某一区域内某个数像素来自子图像A ，而其领域内大多数像素却来自子图像B，则将该像素点的系数应用子图像B来替换相应位置的系数。

2.4 图像融合评价体系

本文综合使用定性分析和定量分析评价融合图像的质量[18]。其中定性分析主要基于图像的视觉效果，参考标准为图像清晰度、对比度、亮度等。定量分析主要基于图像评价指标，不同文献采用的评价指标存在不足或冗余。本文将评价指标分为4类：基于信息量的评价、基于图像对比度的评价、基于图像平均灰度的评价、基于图像边缘强度的评价，选取每个类别中最具代表性的指标作为定量评价标准，分别为图像平均灰度、标准差、熵、边缘相似性测度，评价指标值越大，说明图像融合效果越好。

3 实验结果与分析

为了验证本文提出算法的可行性、普适性和实用性，选用CT、MRI、PET等医学图像，分成6组进行测试，每组包括两幅图像：① 脑部MRI-T1加权图像和MRA图像；② 脑部MRA-GAD图像与脑部CT图像；③ 脑部MRI图像和脑部PET图像；④ MRI图像和CT图像；⑤ CT图像和PET图像；⑥ 脊柱CT图像和MRI图像。5组图像经配准和尺寸调整后，大小均为256×256，具有256个灰阶，所用融合算法均在Matlab 2010a开发环境下仿真实现。将本文提出的融合算法与像素平均法[19]、基于取大规则的传统离散小波变换法[20]、NSCT-1[21]和NSCT-2[22]进行比较，融合结果，见图4。

3.1 定性分析

6组图像的融合结果，见图 4。图 a3～a7，b3～b7、c3～c7、d3～d7、e3～e7、f3～f7 分别对应像素平均法、离散小波变换法、NSCT-1、NSCT-2和本文提出算法的融合结果。从视觉效果看，基于本文提出算法的融合图像a7对比度最优；b7图像分辨率最高，且很好的突出脑部CT的细节部分；c7保留了大部分的PET图像信息，突出MRI图像目标区域；d7图像中边界清晰，突出了CT和MRI的细节部分；e7完整结合了PET和CT图像信息，其中PET提示有无功能病变，CT提供衰减校正和定位，图像中小细节部分更加清晰；f7种骨骼图像亮度最高，完美结合CT和MRI的脊柱信息。表明本文融合算法的可行性、稳健性与优越性。

3.2 客观定量评价

不同算法所得融合图像的熵，平均值，标准差和边缘相似性测度，见图5～8所示。可以看出，基于像素平均法获得的熵在6组融合图像中均最小；基于离散小波变换获得的熵值有所提升，但熵值仍然较小；基于NSCT-1和NSCT-2方法的熵值高于前两种方法；基于本文融合算法所得的熵，在6组融合图像中均获得最大值，较其他4种方法提升了0～40%，表明基于本文算法的融合图像信息量最大，融合效果最优。

同理，基于像素平均法获得的平均值、标准差和边缘相似性测度在6组融合图像中均最小；基于离散小波变换获得的3个指标均优于像素平均法，但低于NSCT和本文提出的算法；基于NSCT-1和NSCT-2方法的优于前两种融合算法，但两者之间不具备可比性，这是由于在某些组融合图像中NSCT-1优于NSCT-2；基于本文融合算法所得的平均值、标准差和边缘相似性测度，在6组融合图像中均获得最大值，较其他4种方法分别提升了3%～42%、1%～42%和0.4%～48%，表明基于本文算法适用于CT，MRI和PET任意组合的融合，融合图像边缘强度、对比度、清晰度均最优。

4 结论

多模态医学图像融合技术是一种强有力的图像处理工具，对临床疾病诊断至关重要。本文提出了一种基于NSCT的图像融合改进算法，其中高低频融合规则克服了传统规则的局限性，其中区域均值取大能更好地保留低频信息，高频方向系数区域方差取大可突出图像边缘细节；对于不同模态图像融合，本文提出的算法均能获得高质量的融合图像。定性和定量分析同时验证了本文提出算法优于现存的其他融合方法，具有很强的普适性和稳健性，是一种可行的、有效的图像融合算法，具有较强的临床应用价值。

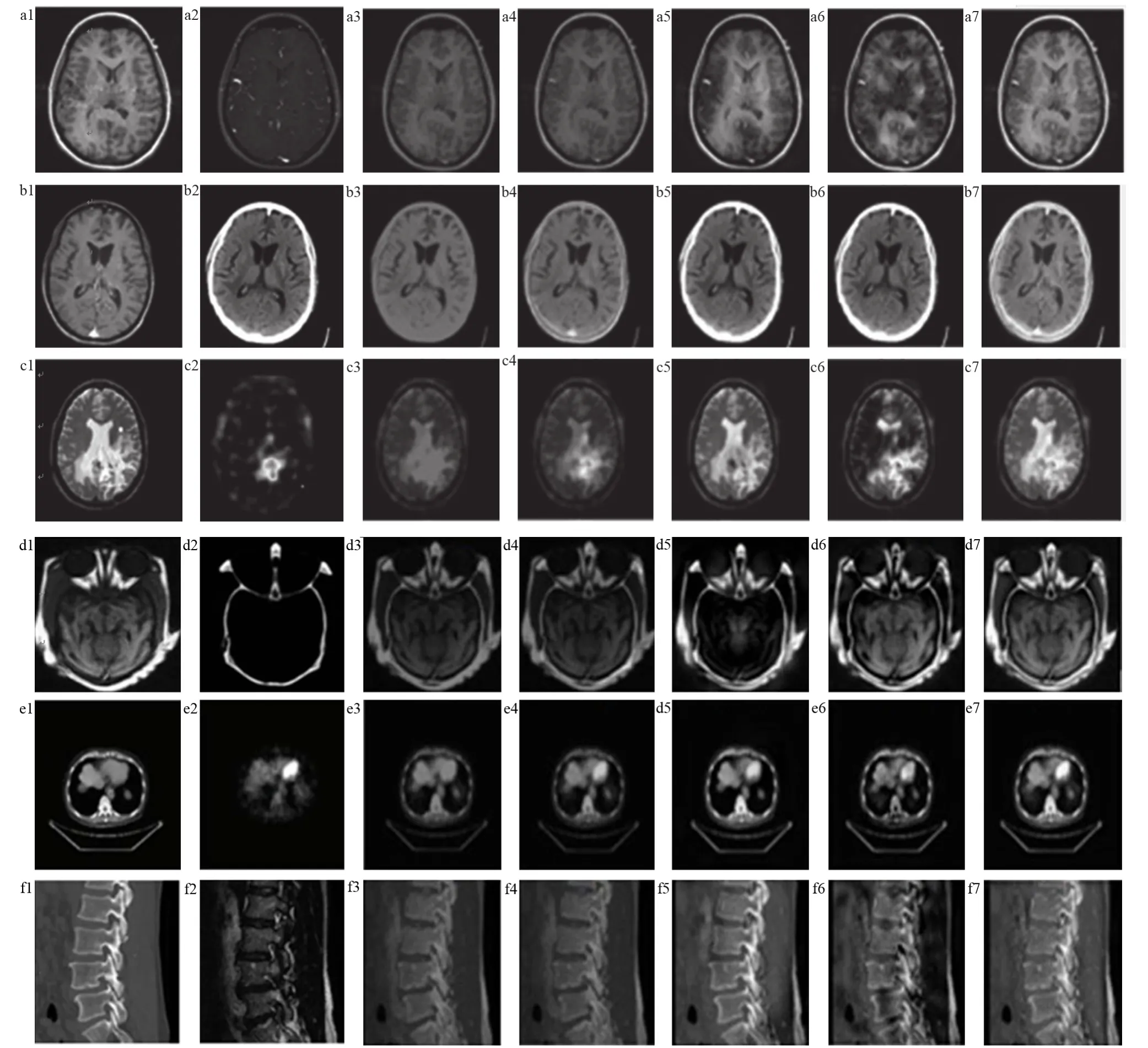
图4 不同融合算法所得的融合图像

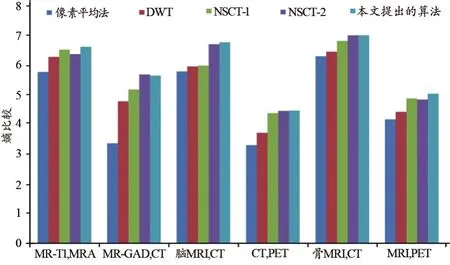
图5 不同融合算法所得的熵比较

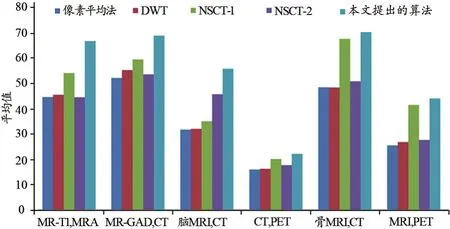
图6 不同融合算法所得的平均值比较

图7 不同融合算法所得的边缘相似性测度比较

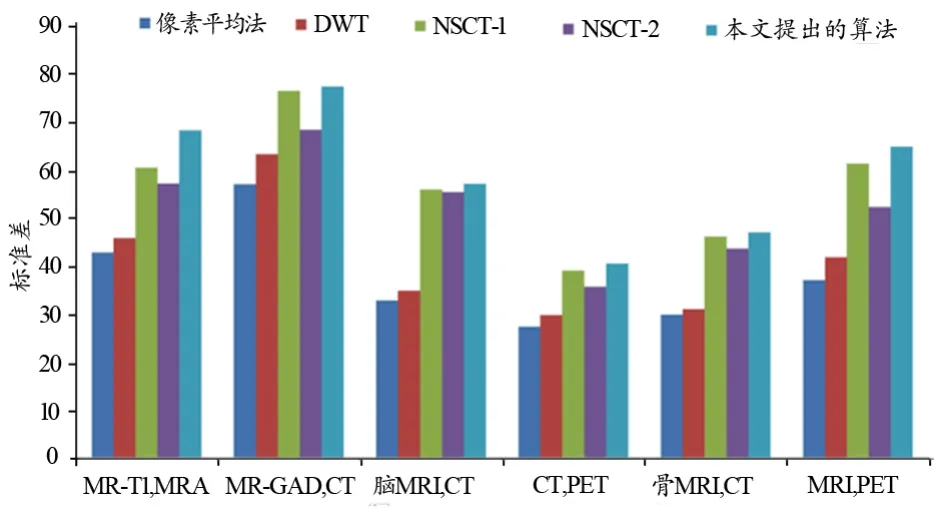
图8 不同融合算法所得的标准差比较

[1] 高峰,李梅,仇振钊.一种多模态医学图像数据融合方法与应用[J].中国医疗设备,2013,28(5):164-167.

[2] 靳珍怡,王远军.基于非下采样轮廓波变换的多模态医学图像融合[J].中国医学物理学杂志,2016,(5):445-450.

[3] 杨勇,童松,黄淑英.快速离散Curvelet变换域的图像融合[J].中国图象图形学报,2015,20(2):219-228.

[4] 赵春晖,郭蕴霆.一种快速的基于稀疏表示和非下采样轮廓波变换的图像融合算法[J].电子与信息学报,2016,38(7):1773-1780.

[5] Adali T,Levin-Schwartz Y,Calhoun VD.Multimodal data fusion using source separation: application to medical imaging[J].Proc IEEE,2015,103(9):1494-1506.

[6] Xu P,Davoine F,Bordes JB,et al.Multimodal information fusion for urban scene understanding[J].Mach Vision Appl,2016,27(3):331-349.

[7] 靳珍怡,王远军.基于非下采样轮廓波变换的多模态医学图像融合[J].中国医学物理学杂志,2016,(5):445-450.

[8] Da CA,Zhou J,Do MN.The nonsubsampled contourlet transform: theory, design, and applications[J].IEEE T ImageProcessing,2006,15(10):3089-101.

[9] Liu Z,Yin H,Chai Y,et al.A novel approach for multimodal medical image fusion[J].Expert Syst Appl,2014,41(16):7425-7435.

[10] Yang Y,Tong S,Huang S,et al.Log-Gabor Energy Based Multimodal Medical Image Fusion in NSCT Domain[J].Comput Math Methods Med,2014,2014(2):1-11.

[11] Yang L,Guo BL,Ni W.Multimodality medical image fusion based on multiscale geometric analysis of contourlet transform[J].Neurocomputing,2008,72(1):203-211.

[12] James AP,Dasarathy BV.Medical image fusion: a survey of the state of the art[J].Inform Fusion,2014,19(3):4-19.

[13] Das S,Kundu MK.Corrections to “a neuro-fuzzy approach for medical image fusion”[J].IEEE T Bio-Med Eng,2015,62(4):1226-1226.

[14] Zhang B,Zhang C,Wu J,et al.A medical image fusion method based on energy classification of BEMD components[J].Optik,2014,125(1):146-153.

[15] 张鑫,陈伟斌.Contourlet变换系数加权的医学图像融合[J].中国图象图形学报,2014,19(1):133-140.

[16] 周生龙,张涛,蒯多杰,等.基于方向区域的NSCT图像融合算法[J].激光与红外,2013,43(2):204-207.

[17] 李栋,王敬东,李鹏.基于NSCT变换和小波变换相结合的图像融合算法研究[J].光电子技术,2011,31(2):87-92.

[18] 王杰雄,齐向阳,李欣伟,等.基于边缘和局部能量的NSCT变换遥感图像融合[J].中国科学院大学学报,2009,26(5):657-662.

[19] 高清河,刚晶,王和禹,等.基于小波变换的多模态医学图像的融合及性能评价[J].生物医学工程研究,2014,33(4):259-263.

[20] 徐磊,崔璨,张华伟,等.基于离散小波变换的多模态医学图像融合改进算法的研究[J].重庆医学,2016,45(21):2885-2889.

[21] Qu XB,Yan JW,Xiao HZ,et al.Image fusion algorithm based on spatial frequency-motivated pulse coupled neural networks in nonsubsampled contourlet transform domain[J].Acta Automatica Sinica,2008,34(12):1508-1514.

[22] Bhatnagar G,Wu QMJ,Liu Z.Directive contrast based multimodal medical image fusion in NSCT domain[J].IEEE T Multimedia,2013,15(5):1014-1024.

A Novel Method for Multimodal Medical Image Fusion Based on Non-Subsampled Contourlet Transform

XU Lei, CAO Yan
Department of Nuclear Medicine, Nanjing First Hospital, Nanjing Medical University, Nanjing Jiangsu 210006, China

ObjectiveIn this paper, a novel method for the fusion of multimodal medical images is proposed based on nonsubsampled contourlet transform (NSCT).MethodsFirstly, the source medical images were initially transformed by NSCT followed by fusing low and high frequency sub-bands. Secondly, the low frequency components of NSCT were fused by the maximum local mean scheme and high frequency components were fused by the maximum local variance scheme. Thirdly, the use of variance enhanced the fusion scheme by preserving the edges in the images. These combinations significantly preserved more details in the source images and improved the quality of the fused images. Finally, the fused image was reconstructed by inverse non-subsampled contourlet transform.ResultsThe efficiency of the suggested technique was carried out by fusion experiments on 6 different multimodality medical image pairs, visually and quantitatively experimental results indicated that the percentage improvement in entropy, mean, standard deviation and edge strength in proposed method were 0～40%, 3%～42%, 1%～42%, and 0.4%～48%compared to conventional methods for 6 pairs of medical images.ConclusionThe proposed method can obtain more efficient and accurate fusion results. It can provide better robustness, superiority and become a feasible image fusion algorithm.

non subsampled contourlet transform; multimodal medical image fusion; fusion rule; medical imaging

TP391

A

10.3969/j.issn.1674-1633.2017.12.015

1674-1633(2017)012-0063-05

2016-11-15

2016-12-23

国家自然科学基金（81271604）。

曹艳，副主任技师，主要研究方向为核医学技术。

通讯作者邮箱：yancao97918@126.com

本文编辑 王静