具有庇护所和收获的SIS模型的全局稳定性分析

童姗姗， 朱玉清， 牛玉俊， 李贞旭

(1. 南阳理工学院 数学与统计学院， 河南 南阳 473004； 2. 南阳市中心医院 磁共振影像科， 河南 南阳 473009)

具有庇护所和收获的SIS模型的全局稳定性分析

童姗姗1， 朱玉清1， 牛玉俊1， 李贞旭2

(1. 南阳理工学院 数学与统计学院， 河南 南阳 473004； 2. 南阳市中心医院 磁共振影像科， 河南 南阳 473009)

讨论了一类具有庇护所和收获的SIS生态流行病模型.应用Hurwitz判据、 Liapunov函数、 LaSalle不变集原理、 数值模拟等方法进行研究， 得到了各平衡点存在的充分条件， 各平衡点的局部和全局性态， 收获努力量和庇护所效应对系统持久生存性的影响. 结果表明, 庇护所的庇护比例经过3个不同取值区间的两个临界值时， 分别引起流行病由地方病变为消失， 捕食者种群由灭绝变为与食饵种群共存， 故庇护所效应具有稳定化作用， 适当调节收获努力量和庇护所比例可消除流行病.

庇护所效应； 生态流行病模型； 全局渐近稳定性； 平衡点

传染病是影响自然种群的重要因素[1-3]， 因此生态流行病模型已经成为众多学者研究的热点之一. 1946年， Crombic通过实验方法将避难所效应引入到食饵-捕食模型[4]， 成为生物理论环保研究的奠基者， 指引学者们通过庇护一定比例或一定数量的食饵来实现系统的持久性生存[5-9]. 因此， 具有避难所的食饵-捕食模型 逐渐成为理论生态学的重要研究课题之一. 然而， 在避难所和生态流行病的基础上， 大多数学者主要研究了食饵种群存在传染病的情形[8-10]， 对于捕食者存在传染病的模型研究结果很少.另一方面， 开发利用生物资源的最优策略问题， 日益成为我们兼顾生态效益和经济效益的重要措施， 因此众多学者就不同的生态问题引入收获系数， 从数学上定量分析收获努力量对合理开发和科学管理资源的影响[11-12]， 但是对于生态流行病模型考虑收获的研究甚少. 综上， 本文提出一类具有庇护所和收获且捕食者有SIS传染病的食饵-捕食模型如下：

式中：X(t),S(t),I(t)分别表示t时刻食饵种群、 捕食者种群易感者、 染病者的密度；mX(t)表示t时刻进入避难所的食饵数量且m∈(0,1)；E1,E2分别表示对食饵种群和捕食者种群的捕获努力量；q1，q2分别表示对食饵种群和捕食者种群的收获系数， 参数a,b,c,e,β,d1,d2,δ均为正常数且有一定生物意义.

1 平衡点分析

令x1=

1) 当E1∈(0,x3)时， 系统(1)有2个平衡点P0，P1；

2) 当E1∈(0,x2)时， 系统(1)有3个平衡点P0，P1，P2；

3) 当E1∈(0,x1)时， 系统(1)有4个平衡点P0，P1，P2，P3.

其中

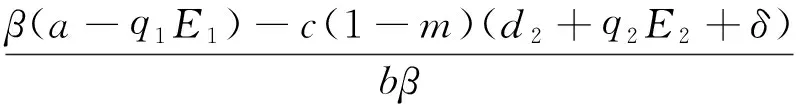
2 平衡点的局部稳定性

系统(1)关于平衡点P(X,S,I)的Jacobian矩阵为

定理1 当E1∈(0,x3)时， 平衡点P0是鞍点， 当E1∈(x3,+∞)，P0局部渐近稳定.

证明将P0(0,0,0)代入J(P)中可得到J(P0) 的特征方程为

(λ-a+q1E1)(λ+d1+q2E2)·

(λ+d2+q2E2+δ)=0,

则λ1=a-q1E1,λ2=-(d1+q2E2),λ3=-(d2+q2E2+δ), 故当E1∈(0,x3)时，P0是鞍点， 当E1∈(x3,+∞)时，P0局部渐近稳定.

定理2 当E1∈(x2,x3)时， 平衡点P1局部渐近稳定，E1∈(0,x2)时，P1是鞍点.

(λ+d2+q2E2+δ)=0,

定理3 当E1∈(x1,x2)时， 平衡点P2局部渐近稳定，E1∈(0,x1)时，P2是鞍点.

证明将

代入J(P)中可得到J(P2)的特征方程为

令

则λ2和λ3是f(λ)=0的两根， 且

λ2·λ3=

故当E1∈(x1,x2)时，P2局部渐近稳定，E1∈(0,x1)时，P2是鞍点.

定理4 当E1∈(0,x1)时， 平衡点P3是局部渐近稳定的.

证明将P3(X*,S*,I*)代入J(P)中可得到J(P3)的特征方程为

λ3+A1λ2+A2λ+A3=0,

令

M1=(a-q1E1)β-c(d2+q2E2+δ),

M2=(a-q1E1)eβ-ce(d2+q2E2+δ)-

d(d1+q2E2)β,

则

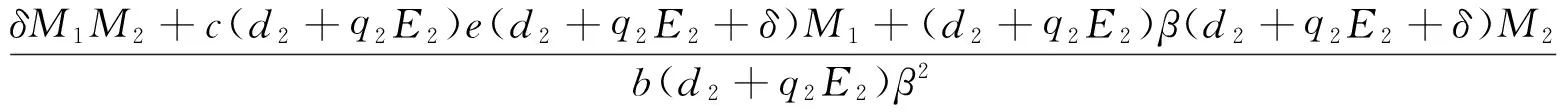
由P3的存在性知，M1>0，M2>0， 从而

综上， 只要P3存在就局部渐近稳定.

3 平衡点的全局稳定性

定理5 当E1∈(x2,x3)时， 平衡点P1是全局渐近稳定的.

证明定义Liapunov函数

则V沿着系统的轨线的全导数

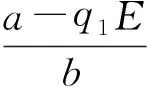
定理6 当E1∈(x1,x2)时， 平衡点P2是全局渐近稳定的.

证明定义Liapunov函数

则V沿着系统的轨线的全导数

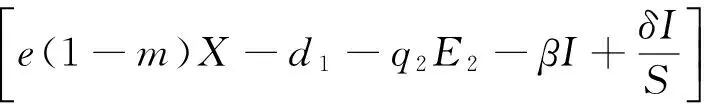
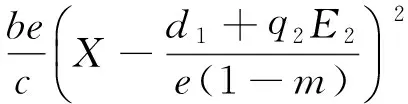
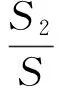
定理7 当E1∈(0,x1)时， 平衡点P3是全局渐近稳定的.

证明定义Liapunov函数

则V沿着系统的轨线的全导数

V′=ω1(X-X*)(a-q1E1-bX-c(1-m)S)+ω2(S-S*)(e(1-m)X-d1-q1E1-βI)+

ω3(I-I*)(βS-d2-q2E2)=-bω1(X-X*)2+(e(1-m)ω2-c(1-m)ω1)(X-X*)(S-S*)+

β(ω3-ω2)(S-S*)(I-I*).

令e(1-m)ω2-c(1-m)ω1=0，ω3-ω2=0， 则有cω1=eω2=eω3， 此时V′=-bω1(X-X*)2≤0， 当且仅当X=X*时取等号， 此时S=S*，I=I*， 因此， 由LaSalle不变集原理知， 当E1∈(0,x1)时， 平衡点P3是全局渐近稳定的.

4 生物意义

4.1 收获的调控作用

下面讨论当食饵的庇护所比例和捕食者的捕获努力量一定时， 收获对系统的稳定化作用， 进而可以通过调节食饵的捕获努力量的值来调节系统的状态， 达到食饵和捕食者种群数量的最大化， 还可以防控流行病， 以取得良好的资源收获.

定理8 1) 若E1∈(0,x1)， 则平衡点P3(X*,S*,I*) 全局渐近稳定， 即食饵种群和捕食者种群都会持续生存， 且疾病会形成地方病；

2) 若E1∈(x1,x2)， 则平衡点P2(X2,S2,0)全局渐近稳定， 即食饵种群和捕食者种群都会持续生存， 且疾病将会消亡；

4.2 庇护所效应的调控作用

下面讨论当食饵和捕食者种群的收获系数和捕获努力量一定时， 庇护所效应对系统的稳定化作用， 进而可以通过调节m的值来调节系统的状态， 使食饵和捕食者种群持续共存， 消除流行病， 实现经济利益和生态利益的统一.

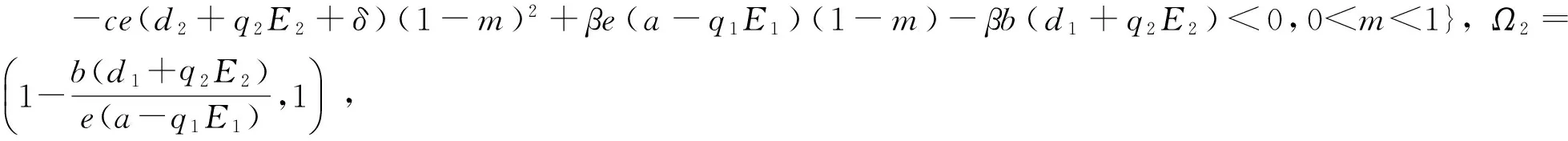
1)若m∈(0,1)/Ω1， 食饵和捕食者种群密度趋向于一个全局渐近的平衡点P3， 食饵和捕食者种群都会持续生存， 且疾病会形成地方病；

2)若m∈[(0,1)/Ω2]∩Ω1， 食饵和捕食者种群密度趋向于一个全局渐近的平衡点P2， 食饵和捕食者种群都会持续生存， 且疾病将会消亡；

3)若m∈Ω2， 食饵和捕食者种群密度趋向于一个全局渐近的平衡点P1， 捕食者种群因缺乏食物资源而灭绝， 食饵种群会持续生存.

可见， 庇护所效应对系统(1)有以下影响：

1)系统的平衡点由不稳定变成全局渐近稳定， 所以庇护所对该收获系统有稳定化作用；

2)疾病由地方病变成消失， 所以庇护所该收获模型有防控疾病的作用；

3)当庇护所效应增强到一定程度后， 会造成食饵资源缺乏， 导致捕食者灭绝， 所以庇护食饵的比例应适当.

5 数值模拟

对于系统(1)， 分别取a1=11.5,b=0.4,c=0.57,e=0.05,d1=0.1,d2=0.12,β=0.05,δ=0.01,q1=0.1,q2=0.2,E1=5,E2=2, 得到如下系统

则

1) 当m∈(0,1)时， 系统(2)有2个平衡点P0，P1；

2) 当m∈(0,0.64)时， 系统(2)有3个平衡点P0，P1，P2；

3) 当m∈(0,0.50)时， 系统(2)有4个平衡点P0，P1，P2，P3；

这里， 零平衡点P0(0,0,0)， 捕食者灭绝平衡点P1(27.5,0,0)， 无病平衡点P2(X2,S2,0)， 疾病平衡点P3(X*,S*,I*)， 其中

X2=10(1-m)-1,

S2=19.30(1-m)-1-7.02(1-m)-2,

X*=-15.11(1-m)+27.50,S*=10.60,

I*=-14.32(1-m)2+28.13(1-m)-10.19.

根据定理2， 可得庇护空间中庇护食饵比例的3个区间分别是(0,0.50)， (0.50,0.64)， (0.64,1). 取相同的两组初值(28,25,22)， (18,15,12)， 对不同的m可得图 1， 其中m=0.1∈(0,0.50)，m=0.52,0.55,0.57,0.59∈(0.50,0.64),m=0.7∈(0.64,1).

图 1(a) 是疾病平衡点P3(X*,S*,I*)的全局渐近稳定图； 图 1(f)是捕食者灭绝平衡点P1(27.5,0,0)的全局渐近稳定图； 需要特别关注的是无病平衡点P2(x2,y2,0)， 因为生态环境的理想状态是消除疾病， 并达到两种群的持久共存. 由图 1(b)～图 1(e) 可以看出， 将食饵种群的庇护比例m控制在区间(0.50,0.64)内， 染病捕食者的种群密度趋于0， 此时疾病消亡， 食饵和易感捕食者的种群密度最终都会稳定地趋向于某个正值， 这就是食饵和捕食者种群的共存平衡密度x2和y2. 又可见共存平衡密度x2和y2不受系统初值的影响， 而受避难所保护食饵种群比例m影响，m越大， 食饵种群的平衡密度x2越大， 捕食者种群的平衡密度y2越小. 另外易得

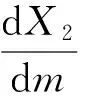
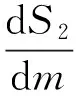
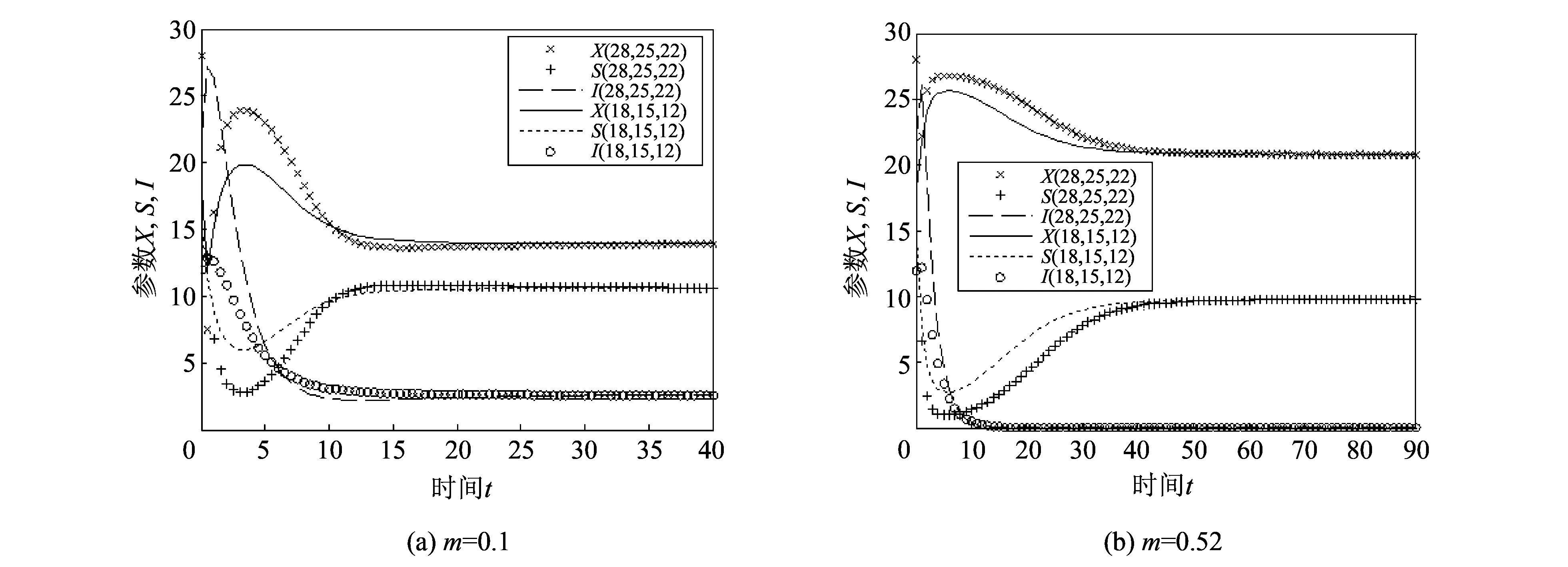
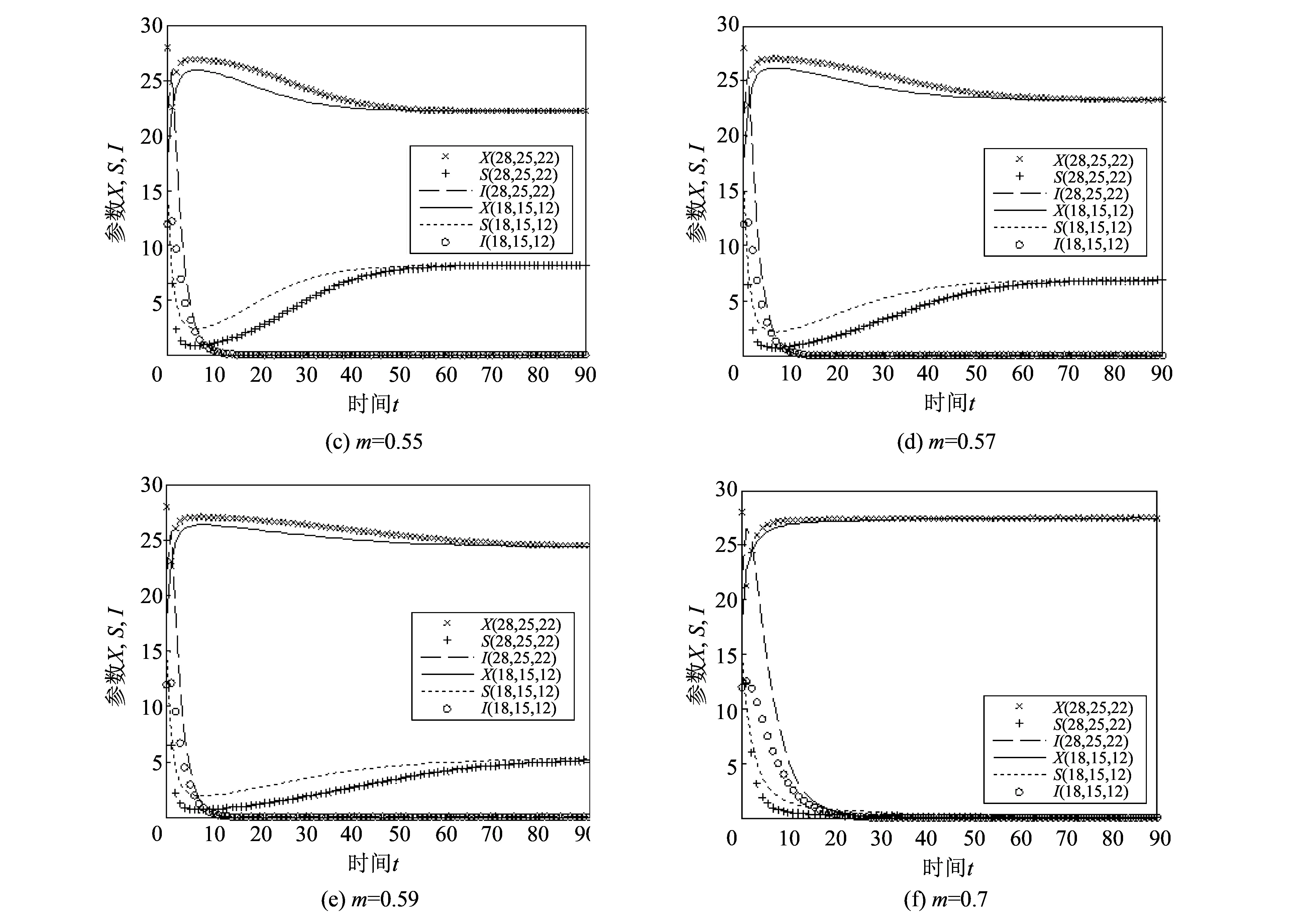
图 1 m不同时系统(2)的数值模拟图Fig.1 Solution curves of system (2) with different m

故在无病平衡点P2(x2,y2,0)的整个存在区间(0,0.64)内， 随着m增加， 食饵种群的平衡密度x2是单调增加的， 易感捕食者种群的平衡密度y2先增后减， 临界值为0.27， 当m趋于0.64时， 捕食者种群的平衡密度y2趋于0， 即易感捕食者种群趋于灭绝， 同时食饵种群的平衡密度趋于27.5， 表明此时两种群密度趋于捕食者灭绝平衡点P1(27.5,0,0).

综上，m∈(0,0.50)时, 疾病平衡点P3(X*,S*,I*)全局渐近稳定,食饵和捕食者种群都会持续生存， 但是SIS传染病形成了地方病；m∈(0.50,0.64) 时, 无病平衡点P2(x2,y2,0)全局渐近稳定,食饵和捕食者种群都会持续生存， 且疾病消亡；m∈(0.64,1)时, 捕食者灭绝平衡点P1(27.5,0,0) 全局渐近稳定, 捕食者种群因缺乏食物资源而灭绝， 只有食饵种群持续生存. 可见， 0.50 和0.64是两个重要的临界值， 当m由0经过0.50时， 流行病由地方病变为消失； 当m由1经过0.64时， 捕食者由灭绝变为与食饵种群共存； 只有当m∈(0.50,0.64)时， 食饵和捕食者两种群处于持久共存的无病状态， 也是生态环境的理想状态， 因此在实践中选取庇护比例时， 须使m处于区间(0.50,0.64)内， 以科学维持生态平衡.

6 结 论

本文研究了一类具有庇护所和收获且捕食者有SIS传染病的食饵-捕食模型， 通过分析系统各平衡点的性态， 得到了收获和庇护所对系统稳定性的影响， 从而给出了控制疾病和实现两种群持续共存的充分条件， 最后进行数值模拟， 为合理开发和管理生态资源提供了理论依据.

[1] 马知恩， 周义仓， 王稳地， 等. 传染病动力学的数学建模与研究[M]. 第1版. 北京： 科学出版社， 2004.

[2] 杨俊仙， 徐丽. 一类具非线性发生率和时滞的SIQS传染病模型的全局稳定性[J]. 山东大学学报(理学版)， 2014， 49(5)： 67-80.

Yuan Junxian， Xu li. Global stability of a SIQS epidemic model with nonlinear incidence rate and time delay[J]. Journal of Shandong University (Natural Science)， 2014， 49(5)： 67-80. (in Chinese)

[3] 张艳， 刘颖芬. 一类捕食者染病的非自治生态流行病模型研究[J]. 中北大学学报(自然科学版)， 2013， 34(2)： 103-108.

Zhang Yan， Liu Yingfen. Analysis of non-autonomous eco-epidemiological model with epidemic in the predator[J]. Journal of North University of China (Natural Science Edition)， 2013， 34(2)： 103-108. (in Chinese)

[4] 郑师章， 吴千红， 王海波， 等. 普通生态学： 原理、 方法和应用[M]. 第1版. 上海： 复旦大学出版社， 1994.

[5] Kar T K. Stability analysis of a rey-predator model incorporating a prey refuge[J]. Commun Nonlinear Sci Numer Simul， 2005， 10(6)： 681-691.

[6] 张丽娜， 李艳玲， 解玉龙， 等. 具有避难所的捕食-食饵模型的全局分歧[J]. 山东大学学报(理学版)， 2007， 42(12)： 110-115.

Zhang Lina， Li Yanling， Xie Yulong, et al. Global bifurcation of a predator-prey system incorporating a prey refuge [J]. Journal of Shandong University (Natural Science)， 2007， 42(12)： 110-115. (in Chinese)

[7] Chen Fengde， Ma Zhaozhi， Zhang Huiying. Global asymptotical stability of the positive equilibrium of the lotka-volterra prey-predator model incorporating a constant number of prey refuges[J]. Nonlinear Analysia， 2012， 3(6)： 2790-2793.

[8] 黄磊， 李自珍， 张丰盘， 等. 庇护效应对一类生态-流行病模型稳定性的影响[J]. 兰州大学学报(自然科学版)， 2008， 44(4)： 103-106.

Huang Le， Li Zizhen， Zhang Fengpan， et al. Influence of prey refuges on the stabilization of an eco-epidemiology model [J]. Journal of Lanzhou University (Natural Sciences) ， 2008， 44(4)： 103-106. (in Chinese)

[9] 王淑璠， 马智慧， 李文龙， 等. 具有庇护所效应的生态流行病模型[J]. 兰州大学学报(自然科学版)， 2013， 49(5)： 703-708.

Wang Shufan， Ma Zhihui， Li Wenlong， et al. Stability analysis of eco-epidemiological model incorporating prey refuges[J]. Journal of Lanzhou University (Natural Sciences)， 2013， 49(5)： 703-708. (in Chinese)

[10] 吉学盛， 毛兴宇. 食饵染病生态流行病系统的稳定性与最优收获[J]. 集美大学学报(自然科学版)， 2015， 20(1)： 71-75.

Ji Xuesheng， Mao Xingyu. The stability of eco-epidemiological model with infected prey and optimal harvesting [J]. Journal of Jimei University (Natural Science)， 2015， 20(1)： 71-75. (in Chinese)

[11] 杨洪娴， 李有文. 具有食饵避难的Leslie-Gower捕食系统最优收获分析[J]. 数学的实践与认识， 2010， 40(20)： 112-117.

Yang Hongxian， Li Youwen. Analysis of a harvested leslie-gower predator-prey model incorporating a prey refuge[J]. Mathematics in Practice and Theory， 2010， 40(20)： 112-117. (in Chinese)

[12] Ji Lili， Wu Chengqiang. Quqlitative analysis of a predatoy-prey model with constant-rate prey harvesting incorporating a constant prey refuge[J]. Nonlinear Analysia， 2010， 11(4)： 2285-2295.

TheGlobalStabilityAnalysisofSISModelwithaPreyRefugeandHarvesting

TONG Shan-shan1, ZHU Yu-qing1, NIU Yu-jun1, LI Zhen-xu2

(1. School of Mathematics and Statistics, Nanyang Institute of Technology, Nanyang 473004, China；2. Dept. of Magnetic Resonance, Nanyang Central Hospital, Nanyang 473009, China)

A SIS epidemic model with a prey refuge and harvesting was investigated. By applying the Hurwitz criterion, Liapunov function, LaSalle's invariable set principle and Numerical simulation, the sufficient conditions for the existence of the equilibrium point, the local and global quality of equilibrium point were analyzed, and the effect of prey refuge and harvesting effort on the system permanence was discussed. The results indicate that, when the proportion of the shelter passes through two critical values of three different intervals, respectively, the epidemic disease is disappearing from the place, the extinction of the predator species become the coexistence of the two species with bait population. So the shelter has a stabilizing effect, adjusting the harvesting effort and the proportion of shelter can eliminate the epidemic proportions, in order to protect the ecological resources.

prey refuge; eco-epidemiological model; global asymptotic stability; equilibrium point

1673-3193(2017)05-0524-07

2016-03-28

国家自然科学基金资助项目(U1504105)； 河南省科学技术基金资助项目(122102210060)； 河南省科技计划项目(1423410107)； 南阳市科技计划项目(RKX06)

童姗姗(1986-)， 女， 讲师， 硕士， 主要从事生物动力系统及数学模型应用研究.

李贞旭(1983-)， 男， 主治医师， 硕士， 主要从事影像医学与核医学研究.

O175.1

A

10.3969/j.issn.1673-3193.2017.05.004