复杂网络上两城市之间疾病传播的建模与分析
2017-12-23潘玮,靳祯
潘 玮, 靳 祯
(1. 中北大学 信息与通信工程学院, 山西 太原 030051; 2. 山西大学 复杂系统研究所, 山西 太原 030006)
复杂网络上两城市之间疾病传播的建模与分析
潘 玮1, 靳 祯2
(1. 中北大学 信息与通信工程学院, 山西 太原 030051; 2. 山西大学 复杂系统研究所, 山西 太原 030006)
针对两城市间不同的迁入迁出对于疾病传播的影响, 建立了复杂网络上的两城市疾病传播SIS (Susceptible-Infected-Susceptible)模型, 证明了无病平衡点的存在性和全局吸引性. 通过数值模拟和参数的敏感性分析发现: 当R0>1时, 在城市之间的往返出行可以将一个城市的局部疫情很快传到另一个城市; 当R0<1时, 疾病在有移民的迁入和人口迁出的城市更容易灭绝, 而当R0>1时, 疾病在有移民迁入和人口迁出的城市传播更慢且疾病规模更小; 进一步得到移民的迁入对疾病传播的基本再生数比较敏感, 从而可以通过增加移民迁入的方式达到控制疾病的目的.
复杂网络; 疾病传播模型; 基本再生数; 敏感性分析
0 引 言
近年来, 伴随着城市和国家之间交通的日益便捷, 人们的出行变得更频繁更方便. 然而, 也带来了诸如SARS[1], H1N1[2]可以在几个月内从一个国家一个地区迅速发展成为全球性流行疫病的问题. 由于出行的便利, 一两个到过疫情爆发地旅行的人在返回其居住地后发病, 进而在其居住地成为传染源引起疾病的爆发, 从而成为全球流行的疫病. 这类危害全球公共卫生安全的问题也引起了流行病学家和生物数学家的极大关注. 在研究传统的流行病动力学时, 往往只考虑疾病在某一地区的传播, 在此基础上, 疾病传播动力学已经取得大量的成果[3-5]. 藉由网络科学在过去20年的迅猛发展, 基于复杂网络的传染病动力学应运而生并取得丰硕的研究结果[6-8].
这里考虑两个城市之间的疾病传播, 由于地理位置的相邻和两城市之间交通工具的便捷, 城市人口往来频繁, 且认为可以在当天返回到其居住的城市. 文献[9]以两社团网络上的疾病传播为研究对象, 考虑了出生、 死亡等人口统计信息的驱动作用, 建立了网络拓扑结构和疾病传播同时演化的确定性SIS模型, 并给出该复杂高维系统的理论分析和模拟结果, 而对于不同城市而言, 由于政治经济地位等各因素导致的差异却没有被考虑. 基于两城市的差异性, 本文考虑人口的迁入和迁出模式不同, 研究该背景下两城市之间的往返出行对疾病传播的影响.
1 模型
根据不同城市的人口迁入迁出的差异性, 假设城市2中人口迁入迁出比较频繁, 且迁入人口都为易感者; 而城市1中人口迁入迁出并不明显, 这里不考虑. 两城市之间往来的人口可以在当天搭乘交通工具返回其居住的城市, 不仅刻画城市内部的疾病传播, 还刻画往来人口在另一个城市期间被当地染病者传染的情形. 使用文献[9]中的变量和参数符号, 给出以下模型
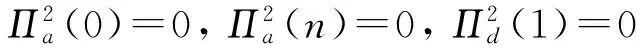

2 基本再生数
在流行病学中, 通常研究疾病的基本再生数R0与1的关系, 用来判断一种疾病是否可以流行[10]. 用文献[11]中的下一代矩阵的方法来计算模型(1)的基本再生数.
V12=V21=(0)n×n,
V22=
根据下一代矩阵的方法, 基本再生数为FV-1的谱半径, 即R0∶=ρ(FV-1). 在具体参数下, 用数值计算给出基本再生数的数值解.
3 平衡点及稳定性分析
由模型(1)得到两城市中的人口规模N1(t),N2(t)满足

对式(1)中前两个方程相加, 后两个方程相加得
可以把式(4)中第二个方程写成
dN2=JN2+R,
其中
N2=(N2,1,…,N2,n)′,
R=(σ2,1A2,…,σ2,nA2)″,

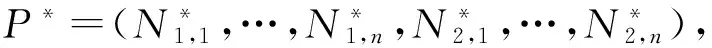
于是模型(1)的极限系统可以写成
(5)
式(5)有唯一的无病平衡点
E0=
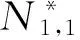
并且有如下的定理,
定理2 在方程组(5)中, 当R0<1时, 无病平衡点E0是全局吸引的.

γI2,k-(k+2)μ2I2,k+μ2(k+1)I2,k+1+
另外, 由M=F-V可以很容易算出M矩阵.
再令
因为R0<1, 则有s(M)<0, 而当ε>0时,s(M+εM1)是连续的, 那么取一个足够小的ε>0, 让s(M+εM1)<0. 这样当t→∞时, 极限系统
(k+2)μ2I2,k+μ2(k+1)I2,k+1+
4 数值模拟
用四阶龙格库塔迭代法, 也就是MATLAB中的ode45求出模型(1)的数值解. 图 1 和图 2 分别给出R0<1和R0>1时, 不同初值条件下两城市中的染病者规模. 其中城市2中的新移民被分配到各人群的概率σ2,k服从λ=40的泊松分布.A2=5 000,μ2=0.006,γ=0.02. 图 1 中的参数取值为τ1=τ2=0.000 1,λ1=0.000 4,λ2=0.001 2, 且R0=0.338 8<1. 其中图 1(a) 的初值条件为I1,40(0)=100,S1,k(0)=S2,k(0)=10 000, 图 1(b) 的初值条件为I2,40(0)=100,S1,k(0)=S2,k(0)=10 000. 从图 1 可以看出, 城市之间的人口出行和当天返回使得其中一个城市的局部疫情很快传到另一个城市, 但由于R0<1, 疾病在城市1 和城市2中最终都消失.

图 1 R0<1时两城市中的染病者规模Fig.1 The infected number at R0<1
图 2 的参数取值为τ1=τ2=0.000 4,λ1=λ2=0.004 8, 基本再生数R0=1.384 2>1. 其中图 2(a) 的初值为I1,40(0)=100,S1,k(0)=S2,k(0)=10 000, 图 2(b) 的初值为I2,40(0)=100,S1,k(0)=S2,k(0)=10 000.

图 2 R0>1时两城市中的染病者规模Fig.2 The infected number at R0>1
由图2可以看出, 由于R0>1, 疾病在两城市中都将持续, 成为地方病. 城市之间的人口往返使得疾病从一个城市的局部发病很快就传到另一个城市, 且在另一个城市引发更多疫情, 从右下角的小图可以看出, 尽管假设两城市内部的传染率相同, 以及从一个城市访问另一个城市的人口在当地被传染的概率也是相同的, 但疾病在城市1中的传播速度比城市2中快, 也就是说, 城市2中的新移民迁入和人口的迁出减慢了疾病的传播, 并且城市1中最终导致的发生率明显高于城市2.
5 敏感性分析及控制策略
通过基本再生数R0对于各参数的敏感性分析, 提出疫情控制和应对策略.
图 3 分别给出了基本再生数R0与城市之间的传染率λ1,λ2和城市2中的人口迁入迁出参数A2,μ2的关系. 图 3(a) 的参数取值:τ1=τ2=0.000 2, 从图中可以看出, 分别改变城市之间的传染率λ1,λ2对于基本再生数的敏感性显然小于同时对λ1和λ2进行改变. 图 3(b) 中的参数为:τ1=τ2=0.000 4且λ1=λ2=0.004 8, 这时, 城市2 中的新移民迁入A2对于基本再生数R0非常敏感, 但迁出率μ2对于R0不敏感. 而且, 增加城市2中的新移民迁入数, 可以减小基本再生数, 进而阻碍疾病的传播, 达到控制疫情的目的.

图 3 R0与各参数的相互关系Fig.3 The influence of the combined parameters on R0
城市之间的短期出行使得一个城市的局部疫情快速地传播到另一个城市, 对于两个城市的情形, 当这两个城市之间彼此都有前往对方城市的短期出行时, 疾病的基本再生数的增加比单一地从一个城市前往另一个城市时要快. 那么, 当一个城市有局部疫情时, 通过控制外来短期出行访问的人数, 同时控制当地人去往其他没有疫情的城市的短期出行, 可以更加有效地控制疾病的传播. 另一方面, 对于有移民迁入和人口迁出的大城市来讲, 增加新移民的迁入, 反而可以有效地控制疾病的传播.
6 结 论
本文考虑人口迁入迁出模式不同的两个城市, 由于地理位置的相邻和交通条件的便利存在频繁的当天往返, 并基于迁移模式的差异性, 建立复杂网络上两城市之间疾病传播模型. 证明了无病平衡点的存在性和全局吸引性. 通过数值模拟, 观察到两城市之间的往返出行可以将一个城市内部的局部疫情很快传播到另一个城市. 当基本再生数R0<1时, 城市2中的移民迁入和人口迁出加快了疾病的灭绝; 当R0>1时, 城市2中的移民迁入和人口迁出不仅减慢了疾病的爆发, 而且降低了染病规模. 而通过敏感性分析, 得出城市2中的移民迁入对基本再生数R0很敏感, 进一步得出了增加城市的移民迁入可以减小基本再生数, 从而阻碍疾病的传播.
[1] Hansen K F. Approaching doomsday: how SARS was presented in the Norwegian media[J]. Journal of Risk Research, 2009(12): 345-360.
[2] Fineberg H V. Pandemic preparedness and response lessons from the H1N1 influenza of 2009[J]. The New England Journal of Medicine, 2014, 370(14): 1335-1342.
[3] Bailey N T J. The mathematical theory of infectious diseases and its applications[M]. New York: Hafner Press, 1975.
[4] Busenberg S, Den Driessche P V. Analysis of a disease transmission model in a population with varying size[J]. Journal of Mathematical Biology, 1990, 28(3): 257-270.
[5] Anderson R M , May R M. Infectious diseases of humans: dynamics and control[M]. New York: Oxford University Press, 1992.
[6] Pastor-Satorras R, Vespignani A. Epidemic dynamics and endemic states in complex networks[J]. Phys. Rev. E., 2001(63): 066117.
[7] 汪小帆, 李翔, 陈关荣. 网络科学导论[M]. 北京: 高等教育出版社, 2012.
[8] 靳祯, 孙桂全, 刘茂省. 网络传染病动力学建模与分析[M]. 北京: 科学出版社, 2014.
[9] Pan Wei, Sun Guiquan, Jin Zhen. How demography-driven evolving networks impact epidemic transmission between communities[J]. Journal of Theoretical Biology, 2015(382): 309-319.
[10] 马知恩, 王稳地, 周义仓, 等. 传染病动力学的数学建模与研究[M]. 北京: 科学出版社, 2004.
[11] Van den Driessche P, Watmough J. Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission[J]. Mathematical Biosciences, 2002, 180(1): 29-48.
ModelingandAnalyzingtheDiseasePropagationBetweenTwoCitiesonComplexNetworks
PAN Wei1, JIN Zhen2
(1. School of Information and Communication Engineering, North University of China, Taiyuan 030051, China;2. Complex Systems Research Center, Shanxi University, Taiyuan 030006, China)
In order to find out the effect of different patterns of immigrations and emigrations on the spread of diseases, a susceptible-infected-susceptible (SIS) model of the disease spread between two cities on complex networks was proposed. The existence of the disease free equilibrium was proved and it is globally attractive. Numerical simulations and sensitivity analysis were performed. IfR0>1, it is observed that the short-time traveling between two cities can quickly spread the disease from one city to another. The disease is easier to die out in the city with immigration and emigration ifR0<1, and the disease spread is slower in the city with immigration and emigration ifR0>1. Moreover, the immigration is sensitive to the basic reproductive number, and the disease can be controlled by means of increasing the immigration.
complex networks; disease spread model; basic reproduction number; sensitivity analysis
1673-3193(2017)05-0518-06
2017-06-05
国家自然科学基金资助项目(11331009)
潘 玮(1986-), 女, 博士生, 主要从事信号与处理方面的研究.
O157
A
10.3969/j.issn.1673-3193.2017.05.003
