基于运动学模型控制的球齿轮齿盘机构万向平台研制
2017-12-23王白王贾巨民许爱芬
王白王,贾巨民,许爱芬
(1.陆军军事交通学院 研究生管理大队,天津 300161;2.陆军军事交通学院 军事物流系,天津 300161)
● 基础科学与技术BasicScience&Technology
基于运动学模型控制的球齿轮齿盘机构万向平台研制
王白王1,贾巨民2,许爱芬2
(1.陆军军事交通学院 研究生管理大队,天津 300161;2.陆军军事交通学院 军事物流系,天津 300161)
基于运动学模型控制的球齿轮齿盘机构万向平台,可用于对控制精度要求不高的场合,实现平面运动向球面运动的转换。在对球齿轮齿盘机构运动学进行分析的基础上,设计万向平台机械结构和控制方法。最后利用ADAMS仿真验证了该平台控制精度,能够满足实际应用要求。
球齿轮齿盘机构;运动学方程;PLC控制;ADAMS仿真
球齿轮机构是一种具有两个自由度,可用来传递二维回转运动的新型齿轮机构,在改变机构传动方向上有独特的优势。当一个球齿轮齿数为无穷多时,其分度球半径将趋于无穷大,球齿轮机构就演变成了球齿轮齿盘机构,它能够实现球面运动和平面运动之间的转换。因此,凡是需要实现姿态控制和柔性连接的场合都可用该机构作为传动执行机构,可广泛应用在航空航天、武器制导和机器人等领域。
潘存云等[1-3]对渐开线环形齿球齿轮的基本概念、啮合原理、结构特点、运动学方程等作了系统研究,对球齿轮的齿廓方程进行了推导,提出了3种齿廓切制方法;姚齐水等[4]提出了一种简便的球齿轮实体建模方法;李婷[5]研究了装配误差对球齿轮传动机构定位精度的影响;高翔等[6]研究了球齿轮柔性轴的姿态算法;李强等[7]设计了一种利用动力学模型精确控制的球齿轮齿盘机构定向平台。上述文献奠定了球齿轮机构应用研究的基础。
由于球齿轮齿盘机构传动运行速度较低,在一些对控制精度要求不高的场合,不需要使用复杂的动力学模型进行控制[7]。因此,本文设计一种基于运动学模型控制的球齿轮齿盘机构万向平台,该平台由机械本体和控制系统两部分组成。其中机械本体为球齿轮齿盘机构,控制系统为基于PLC的步进电机驱动控制系统。平台运行时,利用控制系统控制齿盘的运动输入,相应的球齿轮输出与齿盘相啮合的球面运动。该平台电机输出轴负载小,控制系统简便,具有广泛的应用前景。
1 球齿轮齿盘机构基本原理
1.1 球齿轮齿盘机构的形成
如图1(a)所示为一对圆柱齿轮啮合,在图示位置时两齿轮中心连线与两齿轮的极轴相重合。将这一对相互啮合的圆柱齿轮剖面(图中阴影部分)绕极轴旋转360°便得到一对相互啮合的球齿轮(如图1(b)所示),圆柱齿轮中有关的各种圆,相应的此时全部演变为相应的球[8]。如图1(c)所示,将两齿轮分别安装在一组两自由度的万向框架上,使其绕各自中心作定点运动,就可以实现一对节球的纯滚动。如图2所示,当一个球齿轮的分度球半径为无穷大时,球齿轮演变为一个平面齿环,过齿环中心的剖面所截得的齿形为一个标准齿条,此时球齿轮机构就演变成为球齿轮齿盘机构,其中球齿轮作球面运动,齿盘作平面运动。因此球齿轮齿盘机构可以实现平面运动和球面运动的相互转换。

图1 球齿轮机构形成示意

图2 球齿轮齿盘轮机构示意
1.2 球齿轮齿盘机构的运动学分析
如图3所示,建立如下坐标系:
(1)固定坐标M10=[O10,x10,y10,z10]和M20=[O20,x20,y20,z20]。
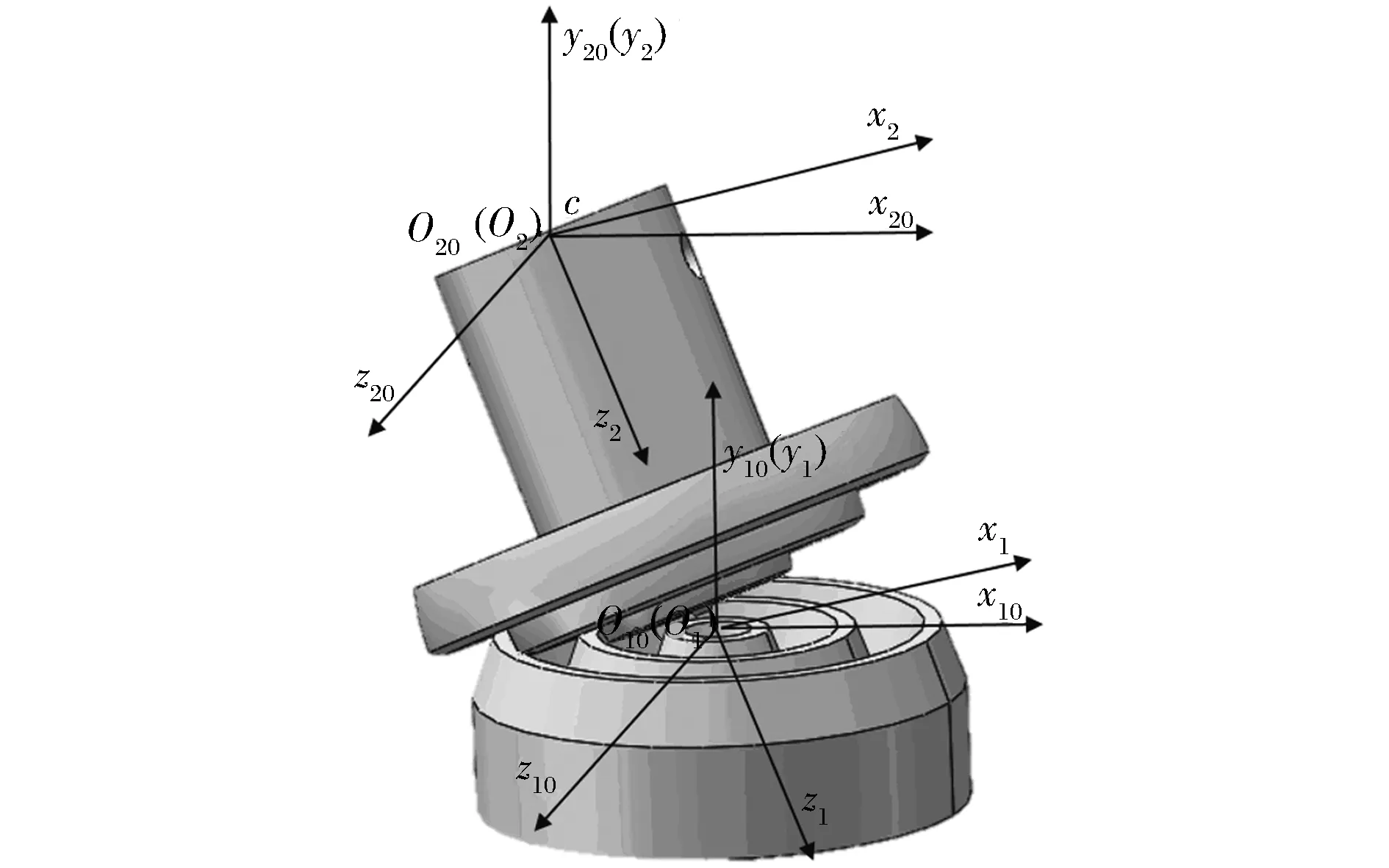
图3 球齿轮齿盘机构坐标系
(2)齿盘固连坐标M1=[O1,x1,y1,z1]。
(3)球齿轮固连坐标M2=[O2,x2,y2,z2]。
在球齿轮齿盘机构中,球齿轮的分度球与齿盘的节平面作纯滚动。设球齿轮的分度球半径为r,则齿盘极轴末端初始位置的坐标和球齿轮输出轴末端C点初始位置坐标均为(0,r,0)。当球齿轮从初始位置往任意方向偏转θ时,在包含该方向的截面内,球齿轮齿盘的运动等同于普通圆柱齿轮与标准齿条的啮合运动。球齿轮的偏转角θ与齿盘的移动距离S有如下关系:
S=rθ
(1)
当齿盘为主动构件时,其输入参数为x轴方向和z轴方向的位移sx和sz,输出参数为输出轴端点坐标(xc,yc,zc)。齿盘移动的距离S和方位角α分别为
(2)
输出轴端点坐标(xc,yc,zc)为
(3)

当球齿轮作为主动件时,其运动为球面的偏转运动,该运动可以视作分别绕x轴和z轴的分转动的合成。因此,其输入参数为分别绕x轴和z轴转动的角度βx和βz,输出参数为齿盘的位移(sx,sz)。
根据旋转变换坐标转换公式可得
(4)
式中Rx、Rz分别为绕x轴和绕y轴的旋转矩阵。
因为同一点在同一坐标系下坐标相同,因此式(3)与式(4)相等
(5)
解式(5)可得偏转角θ和方位角α为
(6)
联立式(1)、(2)、(6)可解出齿盘位移为
(7)
2 万向平台结构设计
2.1 万向平台机械本体
万向平台结构由机械本体和控制系统两部分组成。图4为该万向平台的机械本体实物。电机通过丝杠滚珠机构驱动,使滑块a和b分别沿x轴和z轴方向滑动;齿盘通过基座固连在滑块a上,其运动为滑块a和b的合成运动;圆环与支架铰接,球齿轮通过横轴与圆环铰接,球齿轮可以在空间内做两自由度的转动,且转动中心位于圆环的中心位置;齿盘与球齿轮相互啮合,齿盘的平面运动转化成球齿轮的球面运动;球齿轮输出轴末端可以根据设计加装不同类型的装置,跟随球齿轮做牵连运动。根据以上分析,可知该平台自由度为2,原动件与系统自由度相等,因此该平台具有确定的运动。

图4 万向平台机械本体实物
2.2 万向平台控制系统
如图5所示,万向平台控制系统主要由计算机、PLC、步进电机驱动器和步进电机组成。控制系统控制原理是利用计算机软件编程控制PLC产生脉冲,通过脉冲的个数来控制电机角位移量,达到定位的目的;同时通过控制脉冲频率来控制电机转动的速度,达到调速的目的。
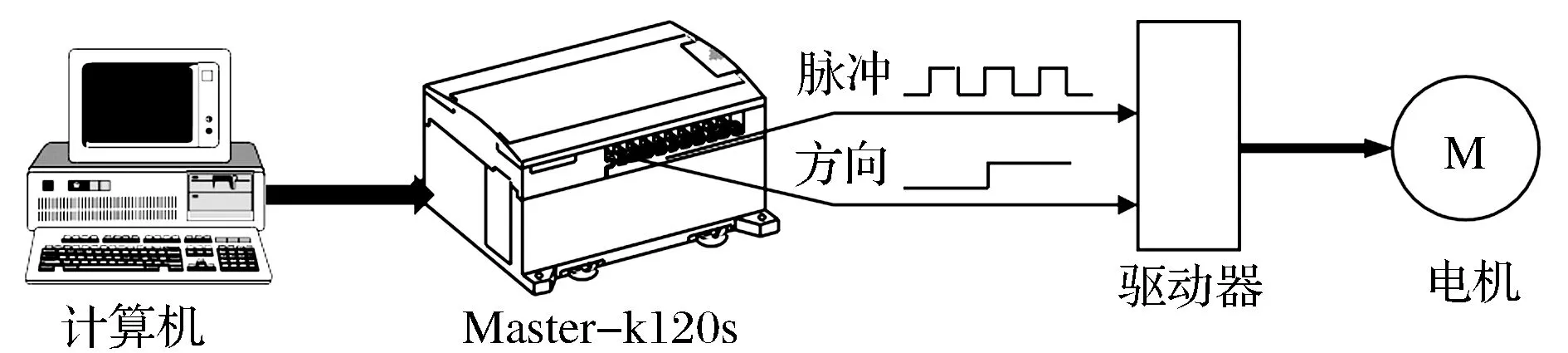
图5 万向平台控制系统示意
3 万向平台控制方法设计
3.1 万向平台控制流程
万向平台主要功能是将平面运动转换成球面运动,平台运行控制流程如图6所示。

图6 万向平台控制流程
3.2 万向平台运动学模型
万向平台控制的基础是对运动学模型的求解,运动学模型包括正向运动学模型和逆向运动学模型。正向运动学模型是指在已知齿盘运动状态的条件下求解球齿轮输出轴末端点的运动状态;逆向运动学模型是指在已知输出轴末端点运动状态的条件下,确定齿盘的运动状态。由于万向平台是根据球齿轮输出轴末端的运动轨迹来确定齿盘的运动输入,因此关键是建立逆向运动学模型。
以该平台球齿轮输出轴末端为坐标原点,建立如图4所示的坐标系。设球齿轮中心至输出轴末端点距离为l,分度球半径为r,用s1表示齿盘沿x轴位移,s2表示沿z轴位移,根据式(1)和式(2)可算出球齿轮的偏转角θ和方位角α
(8)
由式(7)、(8)可得
(9)
根据式(9)可计算出s1和s2,进而可以计算出电机的驱动参数。
3.3 电机驱动参数计算
由于逆向运动模型求解出的仅仅是齿盘x轴方向和z轴方向上的位移,还需要将该位移换算成电机角位移和脉冲数。计算公式为
角位移=齿盘位移/螺距
脉冲数=角位移/(步距角×驱动器细分数)
PLC通过位置控制功能控制对电机的脉冲输入。位置控制是指从起始地址到目标地址,地址表示每一时刻电机的位置,其值大小用脉冲数表示。位置控制功能有位置的绝对控制和位置的相对控制两种运行方式,不同的运行方式对地址的计算方法有所区别。
(1)位置的绝对控制。这种方式需要指定原点地址,其在程序中写入的是目标地址。目标地址是相对原点的有向距离,有正有负。电机的转向决定于位置转移量的符号,转移量等于起始地址和目标地址之差。如果开始地址<目标地址,则转移量为正,电机正转;相反,如果开始地址>目标地址,则转移量为负,电机反转。如图7所示,起始地址是1 000,目标地址是8 000,转移量是8 000-1 000=7 000,符号为正,表示电机正转7 000个脉冲控制的角位移量。
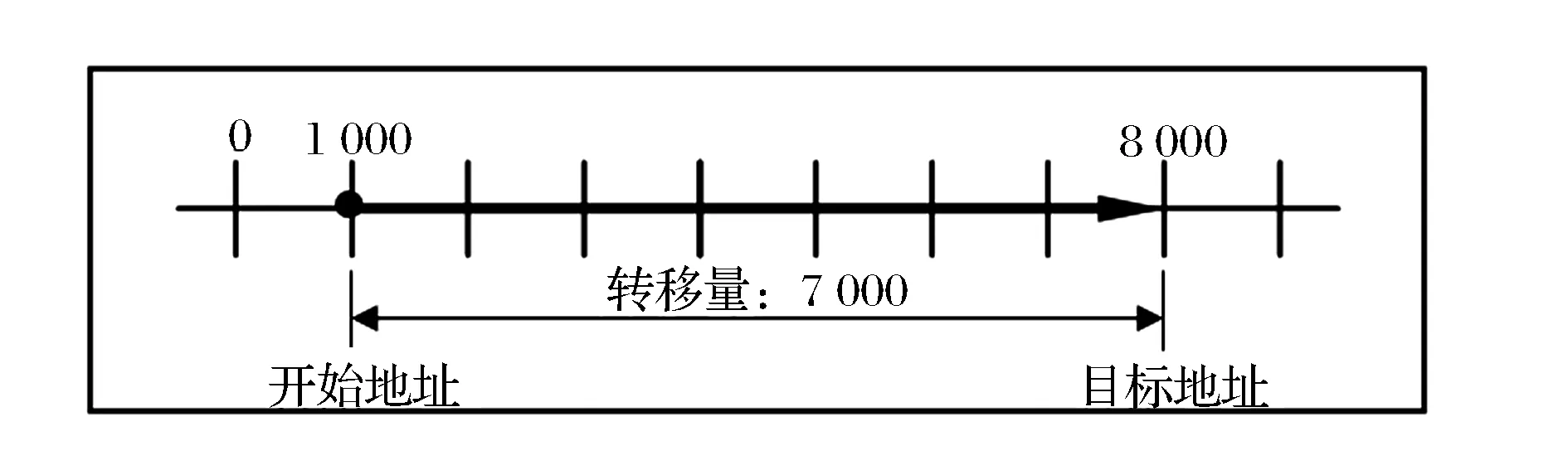
图7 位置的绝对控制示意
(2)位置的相对控制。这种方式直接在程序中写入位置的转移量,转移方向决定于转移量的符号。如图8所示,起始位置为5 000,转移量为-7 000,表示电机反转7 000个脉冲控制的角位移,所到达的目标地址为5 000-7 000=-2 000。

图8 位置的相对控制示意
选定位置控制方式之后可进行计算机编程。
3.4 PLC编程
在计算机中对PLC进行编程控制。由于电机的转动一般是非匀速的,无法直接通过编程实现连续控制,只能将其运动数据离散化。离散化的思想是将电机的转动按一定的时间间隔,划分为若干子区间,当时间间隔足够小时,可近似认为在每个子区间内电机作匀速转动。以位置的绝对控制为例说明利用离散化思想编程需要的基本参数:
(1)记ti时刻电机地址为L1,其中L0=0。
(2)时间间隔Δti=ti-ti-1,t0=0(i=0,1,…)。Δti要足够小,保证在ti-1至ti内能将电机转动近似看作匀速转动而不至引起太大误差。
(3)转移量ΔLi=Li-Li-1,L0=0,电机转速vi=ΔLi/Δti(i=1,2,…)。
根据以上参数编写梯形图程序,图9为控制程序流程。

图9 控制程序流程
4 万向平台运动仿真分析
4.1 螺旋运动仿真
用SolidWorks构建万向平台的实体模型,导入ADAMS中,添加相关约束,可得到如图10所示的实体模型。
根据式(8)可以设计平台输出轴末端的运动轨迹,然后将相关参数输入ADAMS中进行仿真,可以得到齿盘在x轴和z轴上的运动规律。
设计输出轴末端点作螺旋运动:球齿轮极轴沿x轴正向偏转30°,然后绕y轴顺时针转动两周,同时输出轴末端点沿z轴正方向上做匀速直线运动,最后回到原点,运动轨迹如图11所示。采用一般驱动进行仿真,可以得到齿盘在x轴和z轴上的位移,如图12和图13所示。

图10 万向平台机构实体模型

图11 输出轴末端点螺旋运动轨迹

图12 齿盘x轴方向位移
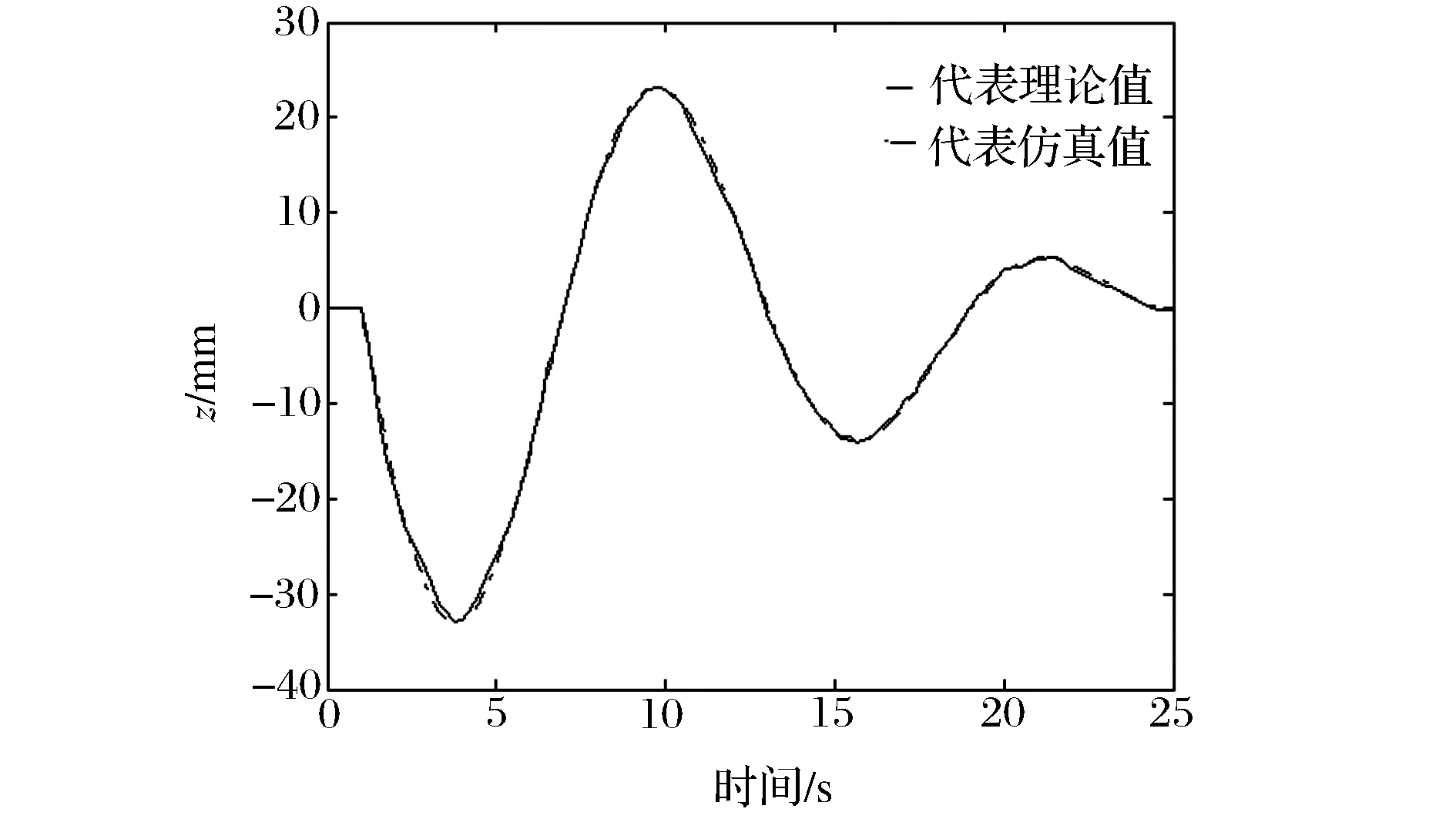
图13 齿盘z轴方向位移
4.2 仿真结果分析
将图12与图13中位移仿真结果与理论计算结果进行对比,其中实线代表理论值曲线,点划线代表仿真值曲线。可看出两种曲线基本重合,说明齿盘位移的仿真值和理论计算值偏差较小。其中,齿盘在x轴方向上两种位移曲线偏离程度最大的区间,是在运行至约1 s时负向位移最大值点附近,最大偏离值为0.84 mm;齿盘在z轴方向上两种曲线偏离最大的区间,在约4 s时负向位移最大值点附近,最大偏离值为1.27 mm。两图中曲线均在位移最大值点附近产生了较大程度的偏离,主要原因是由于在这些区间中速度方向发生改变,导致既有负向位移,又由于速度方向变化产生了方向相反的正向位移。而且这些区间内平均速度较大导致正负位移在数值上均较大,而软件在划分运行步时将速度方向变化的时刻划分在了区间内部,导致仿真值是被正负位移相互抵消后的结果,因而与理论值有较大偏差。除此之外,在其余区间内两种曲线只有微小程度的偏离,这种误差的来源可能是由于ADAMS建模时球齿轮齿盘机构的相关参数不够精确产生的,也可能是对球齿轮中心至输出轴末端点距离测量不准确造成的。
通过计算可知,在x轴和z轴方向上位移理论值和仿真值的最大误差仅占总位移值的1.12%和2.54%,符合一些对控制精度要求不高的低速传动机构的误差标准,证明基于运动学模型控制的球齿轮齿盘机构万向平台是能够满足实际应用要求的。
5 结 语
本文分析了球齿轮齿盘机构的形成原理,推导了球齿轮齿盘机构的运动学公式。在此基础上,设计了一种基于运动学模型控制的球齿轮齿盘机构万向平台及其控制方法。通过ADAMS运动仿真,分析了仿真过程中误差产生的原因,验证了基于运动学模型控制的球齿轮齿盘机构万向平台是能够满足实际应用精度要求的,为该平台的实际应用奠定了基础。
[1] 潘存云,温熙森.渐开线环形齿球齿轮传动原理与运动分析[J].机械工程学报,2005,41(5):1-9.
[2] 潘存云,温煦森.球齿轮齿廓曲面方程的推导[J].国防科技大学学报,2004,26(4):93-98.
[3] 潘存云,尚建忠,杨昂岳,等.球齿轮机构及其应用[J].机械科学与技术,1997,26(1):43-45.
[4] 姚齐水,李常义,潘存云.渐开线环形齿球齿轮的几何建模及其齿面方程研究[J].机械设计与研究,2006,22(2):60-63.
[5] 李婷.渐开线环形齿球齿轮传动理论研究[D].长沙:国防科学技术大学,2009.
[6] 高翔,刘政华,李明宇.基于球齿轮柔性轴的姿态算法[J].中国测试计数,2008,34(6):4-7.
[7] 李强,潘存云,徐海军.基于渐开线环形齿球齿轮齿盘传动的万向平台动力学建模研究[J].兵工学报,2011(9):1140-1144.
[8] 秦虎,朱小浩,张有兵,等.球齿轮研究发展综述[J].现代制造工程,2008(9):128-131.
DevelopmentofUniversalPlatformforSphericalGearandFlutedDiscMechanismBasedonKinematicsModel
WANG Baiwang1, JIA Jumin2, XU Aifen2
(1.Postgraduate Training Brigade, Army Military Transportation University, Tianjin 30061, China;2.Military Logistics Department, Army Military Transportation University, Tianjin 300161, China)
Universal platform of spherical gear and fluted disc mechanism based on kinematics model can be used in the areas with low requirement of control accuracy, and it can realize the transition from planar motion to spherical motion. After analyzing the kinematics of spherical gear and fluted disc mechanism, the paper designs the mechanical structure and control method of universal platform. Then, it verifies the control precision of the platform with ADAMS, which can meet the requirements of practical application.
spherical gear and fluted disc mechanism; kinematics equation; PLC control; ADAMS simulation
2017-04-17;
2017-06-05.
王白王(1992—),男,硕士研究生;
贾巨民(1965—),男,博士,教授,硕士研究生导师.
10.16807/j.cnki.12-1372/e.2017.12.017
TH132.41
A
1674-2192(2017)12- 0074- 06
(编辑:史海英)
