挖掘定义本质 拓展解题思路
2017-12-22山东省寿光现代中学张益龙
数学大世界 2017年33期
山东省寿光现代中学 张益龙
挖掘定义本质 拓展解题思路
山东省寿光现代中学 张益龙
双曲线的定义是双曲线的重要概念,对它的准确理解与正确运用,对学好双曲线甚至整个圆锥曲线都很有意义。教材对双曲线的定义明确了双曲线上任一点到两焦点的距离之差的绝对值为常数灵活应用双曲线的定义,在解决双曲线上的点与焦点的距离有关的问题时,往往会收到事半功倍的效果。因此,本文揭示它的应用,谈用双曲线的定义解题。
一、求点的轨迹问题

二、解决焦点三角形有关问题
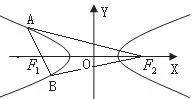

点评:图形具有直观性。本题借助图形,利用第一定义,首先求尔后再求周长,显然是求解问题的一种策略;假若本题未给图形,条件“过F1作直线交双曲线的左支于A,B两点”中再去掉“左支”两字,情况就大不相同,请试一下。
三、求解双曲线离心率问题

∴△AF1F2为直角三角形,


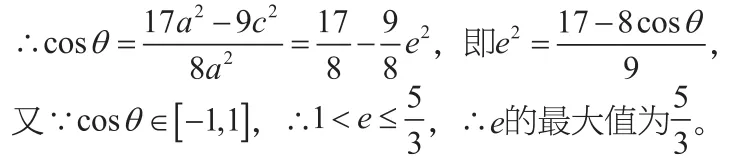
点评:本题中通过三角形的余弦定理建立离心率e关于cosθ的关系式,利用三角函数值域的有界性,从而确定离心率e的范围,得出最值。
四、直线与双曲线位置关系问题
解析:由图及双曲线的几何性质知:
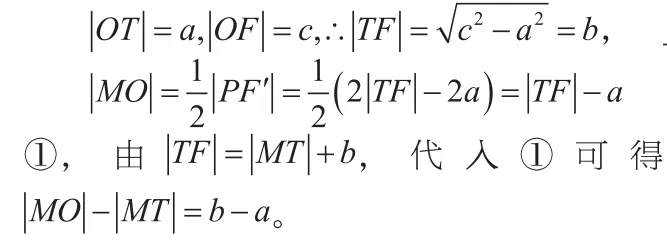

点评:本题重点考查的是双曲线的定义的应用,难点是通过切线性质、三角形中位线的性质转化为定义形式。该题对双曲线知识的灵活应用提出了较高的要求,是今后考题的一个方法。
在解决双曲线问题时要有应用定义的意识,见到动点到两定点距离之差的绝对值等于常数(常数小于两定点的距离),应想到其轨迹是双曲线,见到双曲线上一点应想到该点到两焦点的距离之差的绝对值为常数,只有这样,才能熟练运用双曲线的第一定义解题。
