扩展卡尔曼滤波在Hg-CEMS中的信号处理研究
2017-12-22段钰锋王双群
骆 毅,程 力,段钰锋,王双群
(东南大学能源热转换及其过程测控教育部重点实验室,江苏 南京 210096)
扩展卡尔曼滤波在Hg-CEMS中的信号处理研究
骆 毅,程 力,段钰锋,王双群
(东南大学能源热转换及其过程测控教育部重点实验室,江苏 南京 210096)
目前,燃煤电厂烟气汞连续监测系统(Hg-CEMS)主要采用冷蒸气原子荧光光谱法(CVAFS)来测定烟气中不同形态汞浓度。针对Hg-CEMS中汞分析仪在检测汞浓度过程中输出的电压峰信号,提出了一种分段多项式拟合(PPF)算法,建立了相应的数学模型和状态空间方程,并采用扩展卡尔曼滤波(EKF)算法对含噪电压峰信号进行了滤波处理。仿真结果表明:PPF模型的拟合效果优于常规经验模型;基于该模型的扩展卡尔曼滤波效果显著,对汞分析仪中电压信号的其他峰型有较强的适应性。该信号处理方法不依赖于系统机理模型,自适应好、滤波精度高,对研制适应我国燃煤电厂特点、价格低廉、测量精度高和具有我国独立知识产权的汞形态/浓度在线监测仪器具有重要的借鉴意义。
汞连续监测系统; 冷蒸气原子荧光光谱法; 汞分析仪; 电压峰信号; 状态空间模型; 扩展卡尔曼滤波
0 引言
汞连续监测系统(mercury continuous emissions monitoring system,Hg-CEMS)中,汞分析仪本身及相应的信号转换传输电路中的噪声,会导致系统最终获得的汞浓度值产生较大偏差。目前,针对上述噪声,大多数研究人员从硬件滤波[1-2]入手进行处理。由于其电路设计相对困难、器件和管路选型繁琐,难免会提高信号处理的成本。
本文采用扩展卡尔曼滤波算法,对汞分析仪产生的含噪电压峰信号进行软件滤波处理。该算法需要获取对象的准确状态空间模型。而目前所建立的模型大多为高斯型[3]和峰尾呈指数衰减型[4],其与实际曲线的整体拟合效果较差。针对上述问题,提出了一种分段多项式拟合(piecewise polynomial fitting,PPF)算法,以提高电压峰信号的模型精度,进而提高扩展卡尔曼滤波精度。
1 PPF算法
基于冷蒸气原子荧光光谱法(cold vapor atomic fluorescence spectroscopy,CVAFS)的汞分析仪,其测定烟气汞浓度的基本原理如下。基态汞原子因吸收激发源发射的波长为253.7 nm的辐射而被激发,激发态汞原子在去激发过程中发出特征波长的荧光。该荧光强度由光电倍增管(photo multiplier tube,PMT)来测定。通过对PMT输出的电压峰信号进行峰面积的求取[5],进而得到被测烟气汞浓度。
针对汞分析仪中产生的电压峰曲线,设采样时间间隔为Δk,k时刻对应的电压值为U(k)。PPF算法包括以下6个步骤。
①上升峰初始点的选取。
当ΔU(k)=U(k)-U(k-1) ≥δ且ΔU(k+1)=U(k+1)-U(k) ≥2δ时,以(k-1)点处为上升峰的初始点,记k1=k-1、U1=U(k-1)。其中:δ为较小的正数,经验值取0.01。
②峰顶点的选取。
当ΔU(k)=U(k)-U(k-1) ≥0且ΔU(k+1)=U(k+1)-U(k) ≤0时,以k点处为峰顶点,记k2=k、U2=U(k)。
③下降峰终点的选取。
当|ΔU(k)|=|U(k)-U(k-1)|≥2γ且|ΔU(k+1)|=|U(k+1)-U(k) |≥γ时,以(k+1)点为下降峰终点,记k3=k+1、U3=U(k+1)。其中:γ为较小的正数,经验值取0.01。
④上升峰的多项式拟合。
记(k1,k2]内的电压曲线为上升峰曲线,在满足香农采样定理及考虑数据处理复杂度的条件下,合理选择采样数据,并采用最小二乘曲线拟合方法对上升峰曲线进行拟合。综合考虑拟合曲线的复杂度及精度来确定多项式的阶数,得到的拟合多项式为:
Uup(k)=a1kn+a2kn-1+…+ank+an+1
(1)
式中:n为多项式的阶数;a1,a2,…,an,an+1为多项式的系数。
⑤下降峰的多项式拟合。
记(k2,k3]内的电压曲线为下降峰曲线,处理方法和步骤④一样,得到的拟合多项式为:
Udown(k)=b1km+b2km-1+…+bmk+bm+1
(2)
式中:m为多项式的阶数;b1,b2,…,bm,bm+1为多项式的系数。
⑥电压峰曲线PPF模型的建立。
结合步骤④和步骤⑤建立的上升峰模型和下降峰模型,得到最终的电压峰曲线PPF模型,如式(3)所示。
(3)
2 电压峰曲线EKF状态空间模型
扩展卡尔曼滤波(extended Kalman filter,EKF)是标准卡尔曼滤波(Kalman filter,KF)的扩展,主要用于非线性系统。其核心思想是:首先,通过对非线性函数进行一阶Taylor展开,忽略二阶及以上阶数,得到近似线性化模型;然后,采用KF实现对目标的滤波估计[6]。该方法广泛应用于导航[7]、图像处理[8]、变形测量[9]等领域。
根据上述建立的PPF模型,确定相应的状态空间模型。记上升峰和下降峰模型的状态量分别为Xa=[a1,a2,…,an,an+1]T,Xb=[b1,b2,…,bn,bn+1]T。由于荧光一旦被检测到,其状态就已经确定,且理论模型不会随时间变化,所以此处系统噪声ω为O(n+1)×1,相应的状态矩阵为单位阵[10],即状态矩阵Φ分别为Φa=I(n+1)×(n+1)、Φb=I(m+1)×(m+1)。
观测量分别为:
Za(k)=a1kn+a2kn-1+…+ank+an+1
(4)
Zb(k)=b1km+b2km-1+…+bmk+bm+1
(5)
观测矩阵分别为:
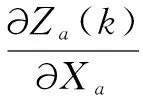
(6)
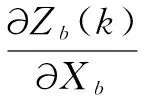
(7)
针对观测噪声v,根据郭从良等[11]建立的光电倍增管相关噪声的数学模型,可以把汞分析仪电压信号中存在的噪声近似为高斯白噪声。
3 仿真结果及分析
为了验证基于PPF模型中扩展卡尔曼滤波的优越性和适用性,本文对Tekran 2600 汞分析系统在某时段的电压峰进行模拟仿真。实际电压峰曲线如图1所示。

图1 实际电压峰曲线
3.1 PPF模型验证
首先,从图1中随机取1个电压峰进行研究。本文取第二个电压峰。由于只是进行模型验证,为了减少工作量,在满足香农采样定理的条件下,选取适当的采样点数。将该峰的PPF模型与整体多项式拟合(global polynomial fitting,GPF)模型、高斯型模型进行对比。各模型的拟合效果对比曲线如图2所示。
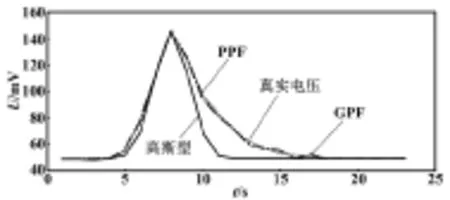
图2 拟合效果对比曲线
仿真过程中,将均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE)作为性能指标,衡量各种模型的拟合效果。拟合效果对比如表1所示。
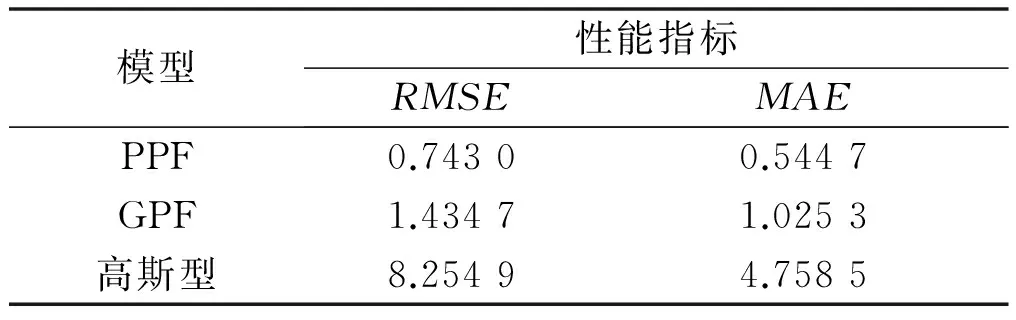
表1 拟合效果对比
其中,RMSE和MAE的具体表达式为:
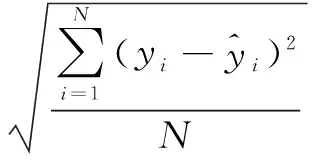
(8)
(9)
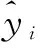
从图2可以看出,PPF模型曲线与真实电压曲线较接近。而GPF模型虽也较接近,但是由于GPF的阶数远高于PPF,将大大增加模型的复杂度;同时,GPF模型会导致无法忽略观测方程的Taylor展开式的高次项,从而使扩展卡尔曼滤波算法产生很大的线性化误差,进而造成该滤波器难以稳定[12]。从表1中的数据可以看出,PPF模型的RMSE和MAE均最小,进一步证明了该模型的优越性。
3.2 基于PPF模型的扩展卡尔曼滤波
基于PPF模型建立电压峰曲线的状态空间方程,并进行扩展卡尔曼滤波处理。在仿真的过程中,观测噪声均值为0、方差为5的高斯白噪声。基于PPF模型的扩展卡尔曼滤波效果及误差(第二个电压峰)如图3所示。
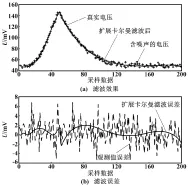
图3 滤波效果及误差(第二个电压峰)
从图3(a)可以看出,扩展卡尔曼滤波处理后的曲线更光滑,且与真实曲线更接近;从图3(b)可以看出,经扩展卡尔曼滤波后得到的电压最优估计值与真实值的偏差很小。由此可见,基于PPF模型的扩展卡尔曼滤波误差小、精度高。
3.3 PPF模型适应性验证
为了检验PPF模型的适应性,在PPF模型第二个峰的基础上,对图1中的另外2个电压峰进行扩展卡尔曼滤波处理。滤波效果及误差分别如图4、图5所示。
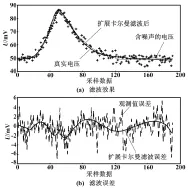
图4 滤波效果及误差(第一个电压峰)
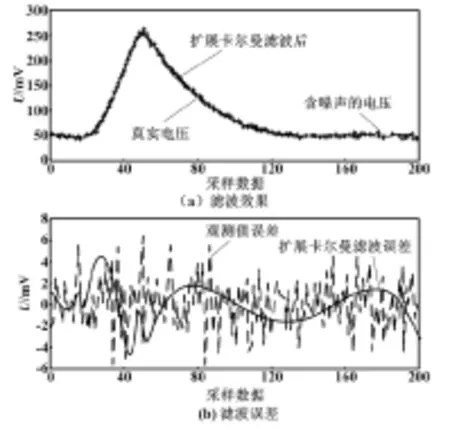
图5 滤波效果及误差(第三个电压峰)
采用RMSE和MAE来评价各个电压峰在相同模型下的扩展卡尔曼滤波效果,对比如表2所示。
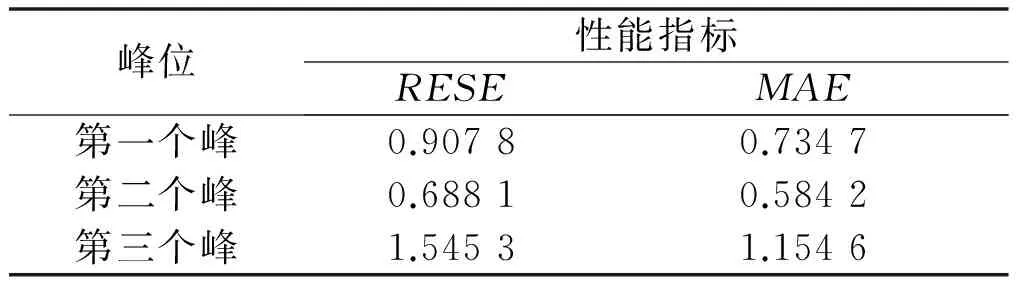
表2 不同电压峰的滤波效果对比
从图3(a)、图4(a)和图5(a)中可以看出,在相同的PPF模型下,不同的电压峰曲线中,采用扩展卡尔曼滤波的效果均较好,说明PPF模型具有较强的适应性。从图3(b)、图4(b)和图5(b)可以看出,第三个峰的滤波误差及误差的波动较大,而第二个电压峰的性能最好。表2显示:第三个电压峰的RMSE和MAE最大,而第二个电压峰的最小。上述现象一方面体现了扩展卡尔曼滤波对模型有较高的依赖性,另一方面体现了PPF模型的适用性仍有待提高。针对上述存在的问题,今后还需对模型和算法作进一步优化,以较好地实现对汞分析仪产生的所有含噪电压峰信号的滤波效果。
4 结束语
针对Hg-CEMS精确机理模型难以确定以及经验模型误差较大的问题,本文从汞分析仪在检测汞浓度过程中输出的电压峰信号入手,建立PPF模型,并基于该模型开展扩展卡尔曼滤波信号处理研究。仿真结果表明,PPF模型的精度明显优于传统经验模型,使得基于PPF模型的扩展卡尔曼滤波算法有很好的滤波效果。针对汞分析仪输出的不同形状电压峰信号,该滤波方法处理效果显著,具有较强的适应性。在满足一定滤波要求的条件下,相对于常规的硬件滤波方法,本文设计的滤波方法更简单、方便、易实施,拓展了扩展卡尔曼滤波的应用领域,为处理Hg-CEMS中汞分析仪的电压峰信号提供了新方法和新思路。
[1] 叶莉华,汪海洋,王文轩,等.基于光电倍增管的低噪声前置放大器的设计及信号处理[J].电子器件,2013,36(3):340-343.
[2] 孙文,千奕,苏弘,等.一种新型低噪声大动态范围小型前端电路的研制[J].原子核物理评论,2015,32(2):202-207.
[3] 暴洪涛.基于单粒子分析方法的水体总菌检测系统关键技术研究[D].北京:中国人民解放军军事医学科学院,2015.
[4] SWARTZENDRUBER P C,JAFFE D A,FINLEY B.Improved fluorescence peak integration in the Tekran 2537 for applications with sub-optimal sample loadings[J].Atmospheric Environment,2009,43(22-23):3648-3651.
[5] YONG C.Atomic fluorescence in environmental analysis[J].Encyclopedia of Analytical Chemistry,2006(9):2270-2292.
[6] 黄小平,王岩.卡尔曼滤波原理及应用:MATLAB仿真[M].北京:电子工业出版社,2015:77-84.
[7] 周敏,刘健,杨林,等.一种自适应卡尔曼滤波在动态导航定位中的应用[J].自动化仪表,2016,37(8):1-4.
[8] 隋婧,董立泉,金伟其,等.一种新的基于神经网络的自适应扫描型红外热像仪非均匀性校正方法[J].中国光学快报,2007,5(2):74-76.
[9] 韩亚坤,文鸿雁,陈冠宇,等.基于神经网络的卡尔曼滤波在变形监测中的应用[J].施工技术,2016,45(1):73-76.
[10]王昕.卡尔曼滤波在模型参数估计中的应用[D].哈尔滨:哈尔滨工业大学,2008.
[11]郭从良,孙金军,方容川,等.光电倍增管的噪声分析和建模[J].光学技术,2003,29(5):636-640.
[12]杨宏,李亚安,李国辉.一种改进扩展卡尔曼滤波新方法[J].计算机工程与应用,2010,4(19):18-20.
ResearchontheSignalProcessingofExtendedKalmanFilterinHg-CEMS
LUO Yi,CHENG Li,DUAN Yufeng,WANG Shuangqun
(Key Laboratory of Energy Thermal Conversion and Control,Ministry of Education,Southeast University,Nanjing 210096,China)
At present,in the mercury continuous emissions monitoring system(Hg-CEMS),the cold vapor atomic fluorescence spectroscopy(CVAFS) is mainly used to determine the concentration of different forms of mercury in flue gas.Aiming at the voltage peak signal output signal of the mercury analyzer in Hg-CEMS for detecting process for concentration of Hg,the method based on piecewise polynomial fitting(PPF) to establish the mathematical model and the state space equation.The noisy voltage peak signal is filtered by using extended Kalman filter(EKF).The simulation results show that the fitting effect of PPF model is better than that of conventional empirical model.Based on this model,the extended Kalman filter is effective and has strong adaptability to other peak types of voltage signal in the mercury analyzer.The signal processing method does not depend on the system mechanism model,and has good adaptability and high filtering precision.It can be used as an important reference for developing the on-line monitoring instrument for the mercury-form/concentration,which is low cost,suitable for China’s coal-fired power plant,and has high measurement accuracy and independent intellectual property rights.
Hg-CEMS; CVAFS; Mercury analyzer; Voltage peak signal; State space model; Extended Kalman filter(EKF)
修改稿收到日期:2017-06-01
国家重点研发计划基金资助项目(2016YFC0201105)
骆毅(1992—),男,在读硕士研究生,主要从事热工自动化与仪器信号处理方向的研究,E-mail:yiluoseu@163.com;程力(通信作者),男,博士,副教授,硕士生导师,主要从事过程自动化控制技术及系统方向的研究,E-mail:chengli@seu.edu.cn
TH89;TP27
A
10.16086/j.cnki.issn1000-0380.201712014
