基于相对定向的图像拼接算法
2017-12-21赵卧龙黄婷婷
赵卧龙, 黄婷婷
(1. 深圳大学 计算机与软件学院,广东 深圳 518060; 2. 深圳中青宝互动网络股份有限公司,广东 深圳518060)
基于相对定向的图像拼接算法
赵卧龙1,2, 黄婷婷1
(1. 深圳大学 计算机与软件学院,广东 深圳 518060; 2. 深圳中青宝互动网络股份有限公司,广东 深圳518060)
针对在现有多张图像拼接过程中,存在匹配误差较大、图像畸形等问题,引入摄影测量学三维相对定向方法,通过解析立体像对进行标定进而求解定向参数,进而生成模型理想像对,再利用视差均值方法对理想像对进行一维配准校准,实现了基于理想像对模型拼接算法。经大量实验结果显示,该算法可有效地减小配准误差和图像配准的计算量,并降低三维物体在二维平面上的图像拼接难度。可见在二维图像拼接中引入该算法是有效的。
图像拼接;相对定向;视差均值;配准误差;理想像对
多张图像拼接融合技术在现代数字图像处理领域中占据重要位置,将多张有重叠区域的不同图像经过提取特征、融合等处理后,可以获得一大张广阔的图像[1]。图像拼接技术在现实生活多个领域都发挥重要作用,如视频监控、虚拟现实、遥感技术及医学等。通常情况下多张图像拼接主要有以下步骤:预处理、变换模型的建立、统一坐标变换、区域配准,融合。而图像配准是图像拼接最关键的技术[2]。由于原始图像拍摄的角度、光的强度、相机分辨率等诸多因素不同,使得待拼接的图像中存在透视变形、旋转、有偏移量等差异。将待拼接图像中找出同名像点进行一一对应,进而转换映射相对关系模型是图像配准的主要工作。目前图像配准的算法大致可以分为三类:基于灰度信息的图像配准方法[3]、基于特征的图像配准方法[4]、基于变换域的图像配准方法[5]。目前存在的二维图像拼接算法,有其成功之处但也都存在着配准误差较大的缺点。
本文根据摄影成像的原理对图像拼接进行分析,认为配准误差产生的根本原因是拍摄图像时产生的上下视差(同名像点的纵坐标之差)和左右视差(同名像点的横坐标之差),提出将摄影测量学中的相对定向模型应用于图像拼接。新的算法基于变换模型理想像对进行算法设计,提出了一种利用左右视差均值进行图像配准的方法。首先利用相对定向技术生成理想像对,然后将生成的理想像对在一维的基础上进行同名像点匹配,进一步消除待拼接像对的左右视差[6-7]。实验结果表明,本文提出的算法可以有效减小图像之间的配准误差。
1算法基础
1.1 特征匹配
特征匹配的目标是找出序列图像中具有共同像点或者区域,进而通过相应匹配方法取得匹配点,最后建立两幅图像之间的变换关系。本文采用特征匹配算法中的双向匹配与最次邻近比算法[8-9]。
匹配过程为:
(1)选取图像A的特征点PL,完全遍历图像B的特征点,寻找与PL距离最近点PR与距离次近点PR1;
(2)若PR/PR1的值小于所设定的阈值,将PR作为PL的候选匹配点,进入步骤(3),否则认为PL在图像B中无对应的匹配点;
(3)再以PR为对应点,完全遍历图像A的特征点,寻找与PR最近的点PL′与次近点PL1′ ,如果PL′ /PL1′ 的值小于所设定阈值,进入步骤(4);
(4)判断PL与PL′是否为同一个点,若是,则记录PL与PR为匹配点对,否则PL在图像B中无对应的匹配点,完全遍历图像A特征点,匹配算法结束。
1.2 相对定向
相对定向是构建本文变换模型理想像对的基础。相对定向是通过不断地重构左右两图像的摄影光束,使得两者的同名光线相交,从而获得与物体模型成比例的几何模型[10-11]。以摄影基线作为空间辅助坐标系的轴,采用两幅图像之间的角元素运动进而实现相对定向,令两张序列图像的投影中心作转轴运动,恢复两张序列图像摄影成像相对关系。单独相对定向有6个角参数:ω1,φ1,κ1,ω1,φ1,它们是左右图像为了使同名光线相交而需要旋转的角度。空间辅助坐标系的X轴为摄影基线,故ω1=0。为求解参数,必须满足两个摄影点S1,S2与物点A在左右图像上的像点G1(x1,y1)、G2(x2,y2)之间的连线与两投影像素点之间连线必须在同一平面上。设a1、a2点的空间辅助坐标分别为(x1,y1,z1)、(x2,y2,z2) ,其共面条件方程为:
(1)
利用泰勒公式对式(1)进行线性化展开处理,并经过推导,可得解算方程式 (2):

(2)
其中5个是待求解参数可知道,当有6个同及以上名匹配点时,可由最小二乘法原理求解,进而迭代计算出定向需要的5个参数。
1.3 理想像对
立体像对水平且摄影基线(两摄站点之间的连线)水平的像对称为理想像对(也称核线影像), 理想像对是一组不存在上下视差但存在左右视差的像对[7-12]。在理想像对上,无论是否存在物体高差,所有同名像点的纵坐标总相等,即其上下视差总为零(如图1所示)。
假设有一张待拼接的原始图像为P,和相对于摄影基线水平的理想像对为P′,在原始倾斜图像P上有像点A的坐标为(x,y),像点A在水平理想像对P′上的坐标系为(u,v),则:像点A在P、P′ 对应关系可表示为:
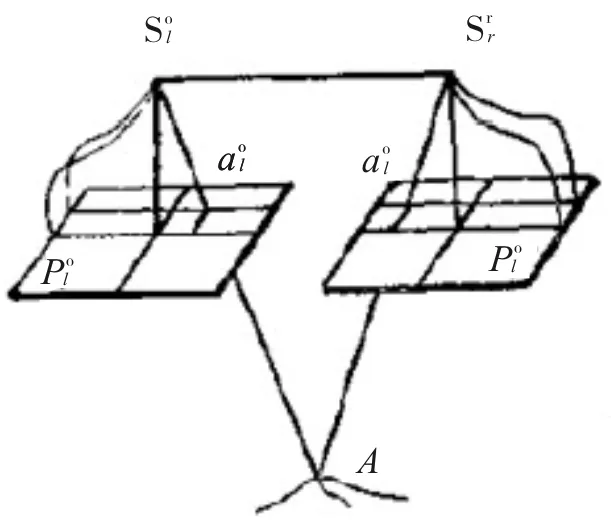
图1 理想像对示意图
(3)
由于理想像对的上下视差总为零,将理想像对作为变换模型引入图像拼接可有效消除待拼接图像的上下视差,简化图像的配准工作,同时也可降低图像配准的误差指数。
2 基于相对定向的图像拼接算法
利用摄影成像的原理将单独相对定向技术引入图像拼接。算法通过重建像对之间摄影光束的约束关系,将待拼接图像转化成理想像对,利用左右视差均值进行图像配准。
2.1 生成理想像对
待拼接图像的特征点检测使用目前常用SURF算法[13],然后利用改进的双向匹配算法进行特征点匹配,得到初始匹配点对,对误配点对进行剔除利用RANSAC算法[14],得到正确的匹配点对。取其中6对同名像点,利用式(2)进行迭代求解,可求得5个相对定向的参数:φ1,κ1,ω2,φ2,κ2。
根据相对定向的参数可以求得变换模型的旋转矩阵R为:
根据单独定向的特性,经过单独像对定向后,两张图像所在的图像平面都平行于摄影基线,最后形成了理想的水平像对。由此根据相对定向参数,可组成的图像旋转矩阵,可以对原始序列影像进行重采样,得原始图像P坐标(x,y),利用式(3)可以得到水平坐标(u,v)。
2.2 利用左右视差均值进行理想像对配准
生成相对理想像对后,需要对同名像点进行一维配准。在实际应用中,高差位移所引起的左右视差并不明显,尤其是生成相对理想像对后,进一步地削弱了高差位移对左右视差的影响。为此,本文提出利用左右视差均值作为待拼接图像序列的整体左右视差值进行图像配准,其步骤如下:
(1)得到相对视差均值Dis,根据原始图像匹配像素点左边计算出水平像素点坐标,根据多个求值,找出左右视差值的最大值和最小值并且减去,进而求出视差均值。
(2)取左右视差均值所在的平面为基准面,即左右视差值与左右视差均值相同的匹配点对所组成的平面,根据左右视差均值确定待拼接图像的重叠区域。
(3)对理想像对进行位移操作即可完成理想像对的配准。
设在相对理想像对中,同名像点的左图像坐标为P(lx,ly),右图像坐标为P(rx,ry),左右视差值为Dis_t=lx-rx,此匹配点对的配准误差为Dis_t-Dis。将所有匹配点对的配准误差相加后取平均可以得到总体的配准误差,其实质为左右视差的加权平均,即:

(4)
判断是否可采用左右视差均值对理想像对进行拼接的标准在于像对之间的最大配准误差是否超过设定的阈值T(根据实际情况设定),如max(Dis,ti-Dis)≤τ,即肉眼无法进行识别的像素范围之内的值。
2.3 配准误差衡量标准
在理想像对上,同名像点的纵坐标总是相等的,上下视差为零,左右视差仍然存在。设物点A在待匹配序列图像上的像点坐标分别为al,ar,另一物点A0在待匹配序列图像上的像点坐标分别为a0l,a0r。现将al,ar,a0l,a0r化为直角坐标系后,可得:
(5)
式中:h为高程;HT为物点到拍摄中心的距离。两式相减后,可得:

(6)
同名像点的横坐标之差称为左右视差p:
p=xl-xr
存在高差位移的像点之间的左右视差较Δp:
Δp=(xl-xr)-(x0l-x0r)
则式(6)可表示为:

(7)
可见,当所拍摄的物体为三维物体时,物体上不同高程的点在理想像对上的左右视差不一致,其左右视差较大小由高程所决定,这是高差位移在理想像对上的体现。当理想像对上同名像点的最大左右视差超过一定范围时,意味着理想像对上的配准误差将超过一定范围,此时理想像对将无法进行拼接。因此,可以采用左右视差较衡量配准误差,对图像配准误差进行定量分析。
3 实验与分析
3.1 实验过程
选取图2进行拼接实验,检验提出的基于相对定向的图像拼接算法的正确性。

图2待拼接图像图3理想像对
在特征点选取阶段,采用SURF-64算法,左边特征点640个,右边600个,采用本文改进的特征提取算法得到162对理想的匹配点,再经剔除误配点后,最终获取157对匹配点对。利用获得的157对匹配点对,根据单独相对定向参数的求解步骤,得到左右图像的旋转矩阵,最终得到相对理想像对,如图3所示。
得到理想像对后,采用左右视差均值的方法对理想像对进行拼接。由于篇幅限制,这里仅给出部分匹配点对的坐标值及其左右视差值,见表1。
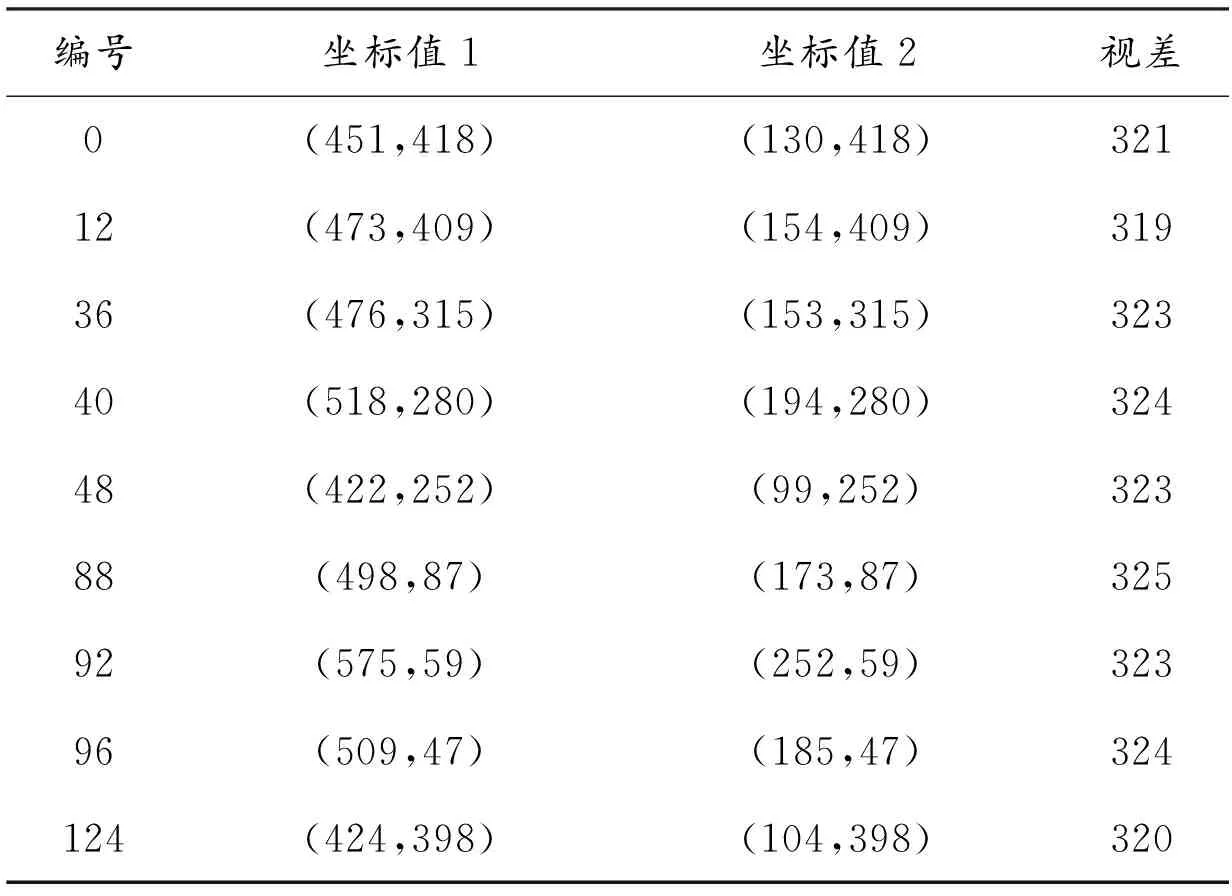
表1 部分匹配点对的坐标值
根据左右视差均值的计算方法可得匹配点对集合的左右视差均值Dis=323 pixel,即取编号为36、48、92的物点所组成的平面为基准面。实验中,选取左右视差均值323 pixel作为像对之间的位移量进行图像配准,配准效果如图4所示。
3.2 实验分析
匹配点对配准误差如表2所示,从表2可看出,实验中157对匹配点所获取的左右视差均值其总体配准误差在1~2 pixel。在生成的理想像对上同名像点的最小左右视差值和最大左右视差值分别为318 pixel和326 pixel,而左右视差均值的取值范围在322~324 pixel,所以理想像对之间可能存在的最大配准误差为6 pixel,满足采用左右视差均值进行拼接的误差范围。

图4 配准效果
为突出接缝处边缘,图4在重叠区域内各选取左右图像的一半进行显示。由于两幅图像存在明显的亮度差异,可直观地分辨接缝处边缘的位置。细看接缝处边缘,未出现任何错位或失真等现象,这也验证了在特定情况下,新算法不仅取得了较好的拼接效果,而且降低拼接算法的计算量。

表2 匹配点对配准误差
单独相对定向方法的配准误差主要来自物体的高差位移所引起的左右视差较,使得无法将重叠区域内所有同名像对都进行配准。为了分析新算法的配准误差,本文对8对经过单独相对定向的同名像点进行数据采集,在基线水平的情况下(即分量By=0、Bz=0,分量Bx、角度w取不同的值)计算它们的最大左右视差较。本文实验设f为固定焦距,H为摄影中心到基准面的距离,h为高差,f/H、Bx/H、h/H分别为摄影焦距、Bx分量、高差与H的比值,f/H=0.02,在不同摄影参数情况下同名像点的左右视差较值如表3所示。
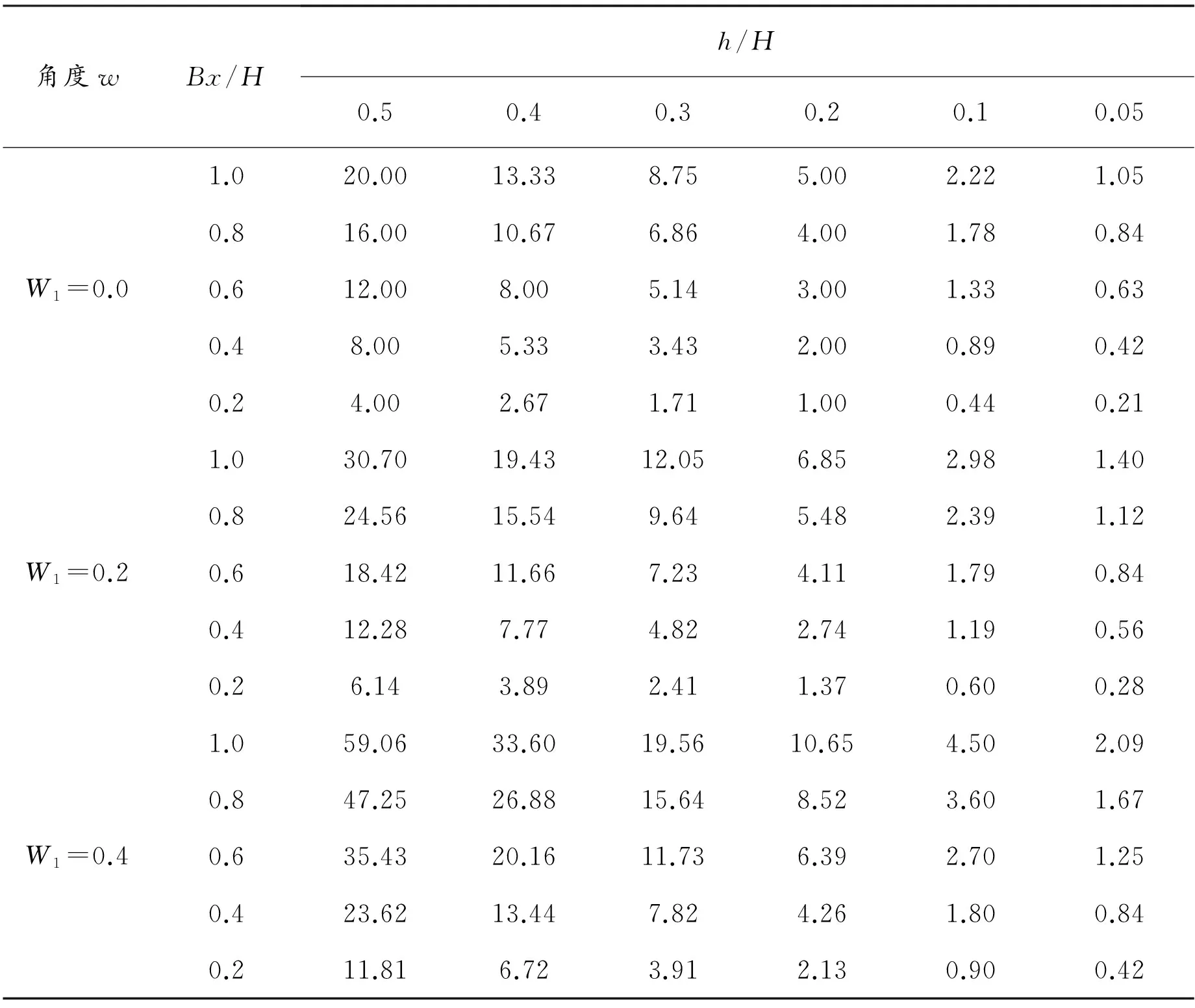
表3 不同参数下同名像点配准误差

表4 透视投影与理想像对模型左右视差比较
由表3可知:角度w与左右视差较呈正比关系。随着角度w的增加,左右视差较也相应增大。 当原图像的角度w较大时,同名像对在水平图像上的左右视差较将被放大,尤其是当高差位移比较明显时,更加无法忽视像对之间的左右视差较。同时,上述实验数据再次验证了高差位移是导致左右视差较产生的基本原因,随着比值h/H的减小,左右视差较也随之减小。当h/H小于一定值时,左右视差较的大小几乎可忽略。由此也可以得到单独相对定向方法仅仅受高差位移的限制,而其他的平面拼接方法还受到了上下视差的限制,本文所提出的拼接方法具有一定优势。
将本文提出的方法与透视投影变换模型[15]进行配准效果比较,设f/H =0.05,摄影方位角分别取-0.2、-0.3、0.2,实验采集的数据如表4所示。
从表4可以看出:在相同摄影条件下,本文模型左右视差和采用传统的透视投影变换模型相比明显较小,并且透视投影变换模型仍然存在上下视差。
4 结论
本文对图像配准中的变换模型进行了深入研究,提出了将摄影测量学中的相对定向模型应用到图像拼接中。利用相对定向模型生成理想像对后,消除了待拼接像对的上下视差,对生成的理想像对在一维的基础上进行同名像点匹配,得到图像接缝处高度契合的拼接图像。实验表明,该方法在配准误差、算法计算量等方面都优于目前现有的算法。由于相对定向方法并未完全消除左右视差对图像拼接的影响,下一步将对消除左右视差进行深入探讨。
[1] 李志刚.边界重叠图像的一种快速拼接算法[J].计算机工程,2000,26(5):37-38.
[2] 王娟,师军,吴宪祥.图像拼接技术综述[J].计算机应用研究,2008,25(7):1940-1944.
[3] 严大勤,孙鑫.一种基于区域匹配的图像拼接算法[J].仪器仪表学报,2007, 27(6):749-751.
[4] 刘小军,周越等.基于轮廓特征的SAR图像自动配准[J].计算机工程,2007,33(4):176-178.
[5]Kuglin,Hines.ThePhaseCorrelationImageAlignmentMethod[C].IEEEInternationalConferenceonCinematieandSociety1975:163-165.
[6] 左森,郭晓松,万 敬,杨必武.宽基线视差图像的拼接算法[J].计算机工程, 2007,33(10):175-177.
[7] 袁修孝,吴珍丽.基于POS数据的核线影像生成方法[J].武汉大学学报,2008, 33(6):560-564.
[8]骞 森,朱剑英.基于改进的SIFT特征的图像双向匹配算法[J].机械科学与技术, 2007,26(9) :1179-1182.
[9]LOWEDG.Distinctiveimagefeaturesfromscaleinvariant-keypoints[J].Internationaljournalofcomputervision, 2004,60(2):91-110.
[10]SMIHTMJ,PARKDWG.TowardsaNewApproachforAbsoluteandExteriorOrientation[J].PhotogrammetricRecord, 1999, 16(94) : 617-623.
[11]张永军,胡丙华.基于多种同名特征的相对定向方法研究[J].测绘学报,2011,40(2):194-199.
[12]李华光.基于数字纠正的核线影像生成方法[J].山东建筑工程学院学报, 2004,19(4) :45-48.
[13]HBay,TTuytelaars,LVanGool.SURF:Speededuprobustfeatures[C].ProceedingsoftheEuropeanConferenceonComputerVision,2006:404-407.
[14]MAFischler,RCBolles.Randomsampleconsensus:aparadigmformodelfittingwithapplicationstoimageanalysisandautomatedcartography[J].CommunicationsoftheACM, 1981(3):381-395.
[15] 钟韬,袁威,左炜亮.系统标定中的透视投影模型[J].兵工自动化, 2011,30(3):30-35.
Imagemosaicalgorithmbasedonrelativeorientation
ZHAO Wo-long1,2, HUANG Ting-ting1
(1.SchoolofComputerScienceandsoftwareengineering,ShenzhenUniversity,Shenzhen, 518060,China; 2.ShenzhenZhongqingbaoInteractiveNetworkCo.,Ltd.,Shenzhen, 518060,China)
Aiming at the problems of large matching error and image deformity in the existing multi-image splicing process, a three-dimensional photogrammetry relative orientation method is introduced to solve the three-dimensional relative orientation of the photogrammetry. Then the parallax average method is used to align and calibrate the ideal image pair, and the ideal image pair model stitching algorithm is realized. The experimental results show that this algorithm can effectively reduce the registration error and the amount of image registration, and reduce the difficulty of the three-dimensional object in the two-dimensional plane image splicing. It is shown that it is effective to introduce the algorithm in two-dimensional image mosaic.
image mosaic; relative orientation; parallax mean; registration error; ideal image pair
2017-07-25
国家语委“十二五”科研规划2014年度重点项目(ZDI123-23)
赵卧龙(1988-),男,河南邓州人,硕士研究生。
1674-7046(2017)05-0086-07
10.14140/j.cnki.hncjxb.2017.05.016
TP391.41
A
