时变非线性结构两阶段损伤识别研究

吴思瑶

(福建农林大学金山学院，福建 福州 350108)

时变非线性结构两阶段损伤识别研究

吴思瑶

(福建农林大学金山学院，福建 福州 350108)

采用Bouc-Wen模型模拟结构的非线性，提出了一种两阶段损伤识别策略，用来检测时变非线性结构在刚度突变情况下的损伤状况。第一阶段，利用小波-独立分量分析(WT-ICA)技术进行突变点识别，从而确定损伤发生的时刻并初步定位损伤；第二阶段，采用结合Bouc-Wen模型的改进多粒子群协同优化算法(IMPSCO)进行分时段参数辨识，从而实现损伤的精确定位和损伤程度确定。通过一个数值算例对所提方法的可行性和有效性进行了验证，结果表明，该方法能够较好地应用于时变非线性结构的损伤评估，并且能够准确地识别出结构的非线性特征。

损伤识别；Bouc-Wen模型；小波奇异性分析；独立分量分析；粒子群优化

目前，基于振动的结构损伤识别研究[1]主要围绕的是时不变线性结构，但实际的土木工程结构通常是时变非线性的，即结构特性(包括质量、刚度、阻尼等)会随时间发生变化且具有一定程度的非线性特征。因此，如何基于结构实时振动数据对这类结构的损伤情况进行快速、准确识别至关重要。为此，国内外学者进行了相关研究并提出了一些方法。Yang和Lin[2]提出了一种基于最小二乘法的自适应追踪方法，对参数缓慢变化和突变的情况均能够获得准确的结果，但该方法必须初始化自适应因子。对此，尹强和周丽[3]通过引入遗传算法提出了一种改进方法，但该方法一般需要通过对加速度积分来获取速度和位移响应数据。Nayyerloo[4]提出了一种实时最小均方根法对非线性结构的时变参数进行识别，但该方法需要同时测量结构的加速度和位移响应。黄致仁[5]利用差分进化算法对单自由度时变非线性结构进行识别，取得了良好的效果，但该方法对多自由度非线性结构的适用性还有待进一步验证。

粒子群优化(Particle Swarm Optimization，PSO)是模拟鸟类和鱼群群体行为的一种智能优化算法，在线性结构参数识别中应用广泛，但对于非线性结构则应用较少。同时，由于Bouc-Wen模型能够模拟工程结构的大部分非线性行为，近年来受到了众多学者的关注和研究[6-7]。因此，本文在Bouc-Wen模型的基础上，将改进PSO算法(IMPSCO)与一种新的突变点识别方法(WT-ICA)相结合，提出了一种两阶段损伤识别方法，用于诊断时变非线性结构在刚度突变时的损伤情况，并通过数值算例对该方法的可行性和有效性进行验证。

1 基本原理

1.1 WT-ICA突变点识别

当结构发生损伤时，动力时程观测信号会在刚度突变的时刻出现无法直接看出的局部间断点，而通过对原信号进行小波变换(Wavelet Transform，WT)，从分解得到的高频细节信号中就可以将刚度突变点识别出来，该过程称为小波奇异性分析。但这种突变点识别方法受噪声影响较大，即原信号的突变信息极可能被噪声淹没。为了解决这个问题，Yang等[8]利用独立分量分析(Independent Component Analysis，ICA)技术，把小波分解得到的高频细节信号进一步线性分解为几个独立分量，进而实现特征提取，识别刚度突变点，该方法称为小波-独立分量分析(WT-ICA)。

假设Y(t)=[y1(t) ,y2(t) ,…,ym(t)]T为经过WT处理得到的m维小波细节信号矩阵，其中包含原始动力时程响应观测信号的突变信息，IC(t)=[IC1(t) ,IC2(t) ,…,ICn(t)]T为利用ICA进一步处理得到的n维独立分量矩阵，那么

yi(t)=ail·IC1(t)+…+aij·ICj(t)+…+ain·ICn(t)(i=1,2,…，m)

(1)

式中，aij表示独立分量ICj(t)在信号yi(t)中的比重大小，称为源分布因子。假设从第k个独立分量ICk(t)中可以识别出突变点，则称之为特征独立分量(Feature Independent Component，FIC)，其对应的源分布因子组成源分布向量A=[a1k,a2k, …,aik,…,amk]T，对A进行处理得到归一化的源分布向量(Normalized Source Distribution Vector，NSDV)：

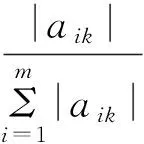
(2)

若a1为NSDV中的最大值，则表示FIC在第i个观测信号中所占比重最大，即第i个观测信号对应的测量位置最可能出现突变因素，进而实现突变点识别。

1.2 基于Bouc-Wen模型和IMPSCO的非线性结构参数辨识

本文采用经典Bouc-Wen模型来模拟结构的非线性，从而建立非线性结构数值模型。多自由度非线性结构的运动方程为：

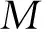
(3)

式中， 、 、X和Z分别为结构的加速度、速度、位移和滞回位移；M为结构质量；C为结构等效粘滞阻尼；R(X，Z，t)为结构的恢复力向量；F(t)为外部激励。对于框架结构，恢复力向量可表示为：

R(X，Z，t)=[R1-R2，R2-R3，…RN]T

(4)

其中，

Ri=aik1X1(t)+(1-ai)kiYiZi(t)

(Ai>0,βi>0，-βi<γi⦤βi，ni≥1，i=1，2，…，N)

(5)

多粒子群协同优化算法(MPSCO)[10]是在标准PSO算法基础上融入仿生学中“协同进化”的思想，很大程度上避免了标准PSO算法的“早熟”现象，即降低了陷入局部极值的可能性。而与常规MPSCO算法相比， IMPSCO算法在寻优质量和算法稳定性方面均得到了一定程度的改善，并且已成功应用于线性结构的参数辨识中[11-12]。IMPSCO算法的改进原理是基于生物学中“自然选择”的思想。若将粒子群的寻优过程看作物种在生物界的自然选择过程，则当某个粒子出现多次被标记为最差的情况时，就表明该粒子适应度低，应将其淘汰，同时用整个种群优良粒子中的重心粒子来替换，进而保证种群的多样性。该算法的具体原理和详细流程，详见文献[13]，本文结合Bouc-Wen模型，提出了基于IMPSCO的非线性结构参数辨识方法，主要包括三个步骤：

(1)待辨识参数编码：需要编码的结构参数包括结构质量、刚度(或弹性模量、惯性矩)、阻尼、Bouc-Wen模型参数等，完成编码后，需要合理设置参数的搜索范围从而确定粒子维数；

(2)IMPSCO算法参数设置：包括子种群数量m(3～5)、子种群大小n(30～50)、优良粒子数量s(5～10)、最差次数限值Lw(5～10)、最大迭代次数Imax(50～500)、学习因子c1和c2以及惯性权重w。一般情况下，当取c1=c2=2且w在[0.9,0.4]之间线性变化时，算法的识别性能较好；

(3)适应度函数建立：按照公式(6)建立适应度函数，从而展开搜索，寻找参数辨识最优解并输出结果。

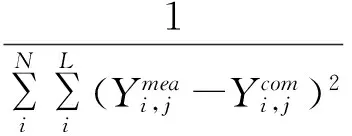
(6)

2 时变非线性结构两阶段损伤识别策略

本文结合WT-ICA突变点识别技术以及基于Bouc-Wen模型和IMPSCO的非线性结构参数辨识方法，提出了一种适用于时变非线性结构的两阶段损伤识别策略。通过第Ⅰ阶段WT-ICA处理实现损伤时刻判断和损伤初步定位，通过第Ⅱ阶段IMPSCO分时段参数辨识实现损伤精确定位和损伤程度确定。

2.1 第Ⅰ阶段

(1)原始信号矩阵集成。将N个传感器观测得到的结构动力时程响应(位移、速度或加速度)集合成原始信号矩阵X(N×l)，l为信号长度。

(2)WT-ICA突变点识别。首先，选择合适的小波函数，通过WT处理对X的每一行数据进行一层小波分解，提取出可能包含损伤信息的小波高频细节部分yi(i=1,2,…,N)，集成矩阵Y(N×l)。其次，利用ICA技术进一步从矩阵Y中提取得到n个相互独立的分量ICj(j=1,2,…,n)，从中确定具有信号突变点的特征独立分量FIC并按照公式(2)计算每个FIC对应的NSDV。

(3)损伤时刻判断和初步定位。通过观察每个FIC中信号突变点对应的时间可以判断损伤发生的时刻。通常损伤发生位置及其附近观测得到的信号突变特征较明显，因此NSDV中最大值点对应的观测点位置就是损伤最可能发生的位置，从而可以实现损伤初步定位。

2.2 第Ⅱ阶段

(1)时间段划分。假设T0和Te分别为结构动力时程响应信号的初始时刻和终止时刻，若存在k个FIC，则有k个损伤时刻Td(d=1,2,…,N)，于是可以将信号划分为k+1段，即T0～T1，T1～T2,…,TN～Te。

(2)IMPSCO分时段参数辨识。首先，对待辨识的结构参数进行编码并设定搜索范围；其次，设置IMPSCO算法的基本参数；第三，根据公式(6)建立的适应度函数，分别对步骤(1)中划分的各个时间段进行IMPSCO参数辨识。

(3)损伤精确定位和程度确定。若结构某个刚度参数明显降低，则表明对应的位置发生了损伤，进而实现损伤的精确定位，同时根据刚度的具体下降值就可以确定出损伤的程度。

3 数值算例

3.1 结构模型

考虑一个底部受到El-centro地震波激励的两层剪切型框架结构。假设结构底层进入非线性状态，基本参数为：质量m1=m2=1kg，前两阶阻尼比ζ1=ζ2=2%，初始层间刚度=102.64 N/m；结构基本周期T=1s；Bouc-Wen模型参数首层屈服位移γ=0.045 m，滞回参数α=0.1，A=1，β=0.5,y=0.5，n=2。假设结构出现两种损伤工况，见表1。仿真时间30 s，采样频率50 Hz，为了模拟环境因素的影响，分别在仿真得到的结构各层加速度数据中添加高斯白噪声，使其信噪比SNR=30 dB，如图1所示，图中a1和a2分别为结构第一层和第二层的加速度，aq为地震加速度，SNR的计算见公式(7)。

(7)

表1 损伤工况

图1 结构各层加速度和地震加速度

3.2 损伤识别与结果分析

按照第2节中的两阶段识别策略，分别对两种损伤工况下的结构进行识别。

(1)第Ⅰ阶段

首先，将结构各层加速度数据集合成原始信号矩阵X(2×1 500)。然后，采用db4小波对X的每一行数据进行一层小波分解，并利用ICA技术进一步处理得到2个独立分量ICj(j=1,2)，如图3所示，根据是否存在突变点来确定特征独立分量FIC并计算每个FIC对应的NSDV，从而完成WT-ICA突变点识别。最后，通过观察每个FIC中信号突变点出现的具体时间就可以判断损伤发生的时刻，而通过判断NSDV中最大值点对应的信号观测点位置就可以初步定位损伤。

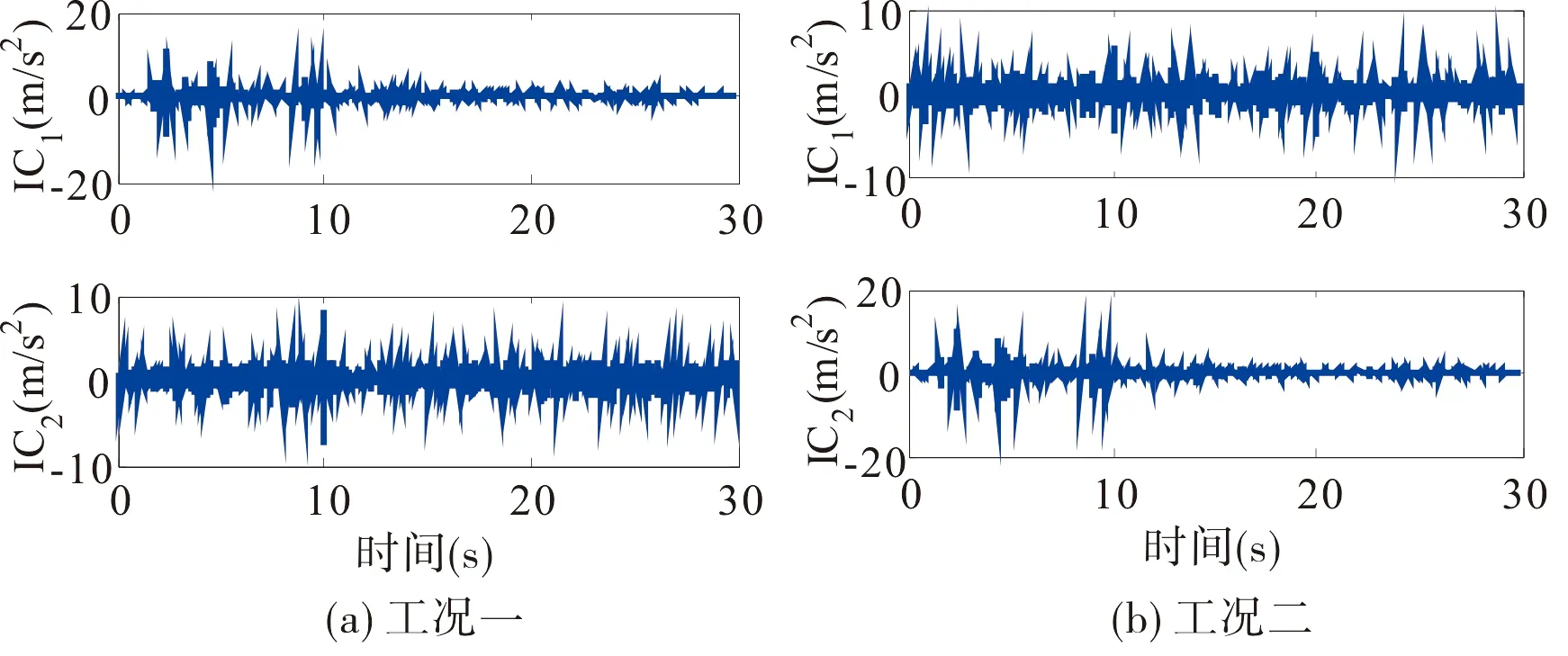
图2 第Ⅰ阶段识别结果

从图2可以看出：在各工况实际损伤发生的时刻，信号中都出现了明显的突变点，相应的分量就是特征独立分量。对于工况一，FIC是IC2，观察确定结构在t=10 s时发生损伤；对于工况二，FIC是IC1，观察确定结构在t=10 s和t=20 s时均发生损伤。这表明对于单损伤和多损伤工况，通过第I阶段识别能够准确判断出损伤发生的时刻。由于工况二(多损伤)的特征独立分量只有一个，即两个损伤信息都包含在一个FIC中，所以无法利用NSDV图来判断损伤，图3为工况一所对应的NSDV图。

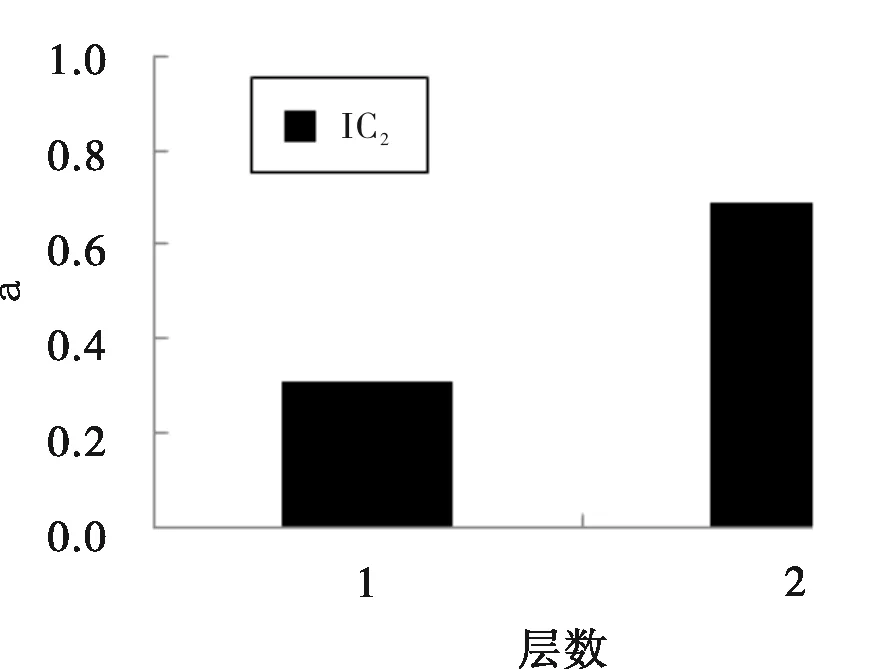
图3 NSDV图

从图3可以看出：工况一的NSDV最大值出现在第2层，即t=10 s时损伤最有可能发生在结构第2层，这表明对于单损伤工况，通过第I阶段识别能够准确判断出损伤发生的位置。

(2)第Ⅱ阶段

首先，根据第Ⅰ阶段中确定的损伤时刻划分时间段。对于工况一，将时间段划分成两段，分别为0～10 s，10～30 s；对于工况二，将时间段划分成三段，分别为0～10 s，10～20 s，20～30 s。在结构各层质量已知的前提下，对待辨识的结构参数进行编码，即k1,k2,ζ1，ζ2,Y,α,β,γ,n,并设置其搜索范围均为理论值的0.5～2倍，故IMPSCO算法的粒子维数为9；同时设置算法基本参数：子种群数量m=3，子种群大小n=10，优良粒子数量s=6，最差次数限值Lw=5，迭代次数Imax=200，学习因子c1=c2=2，惯性权重w在[0.9,0.4]之间线性变化；接着按照公式(6)建立适应度函数，其中测点数N取2；数据长度L取4倍结构基本周期长度，开始分时段参数辨识，辨识结果如图4所示。最后，根据结构刚度的辨识结果就可以精确定位损伤并确定损伤程度。

图4 第II阶段识别结果

由图4可知：各工况下结构刚度退化情况的识别结果均与理论值吻合良好，从而可以精确地定位出损伤发生的位置并对损伤程度作出准确的诊断。具体各结构参数的辨识误差见表2。

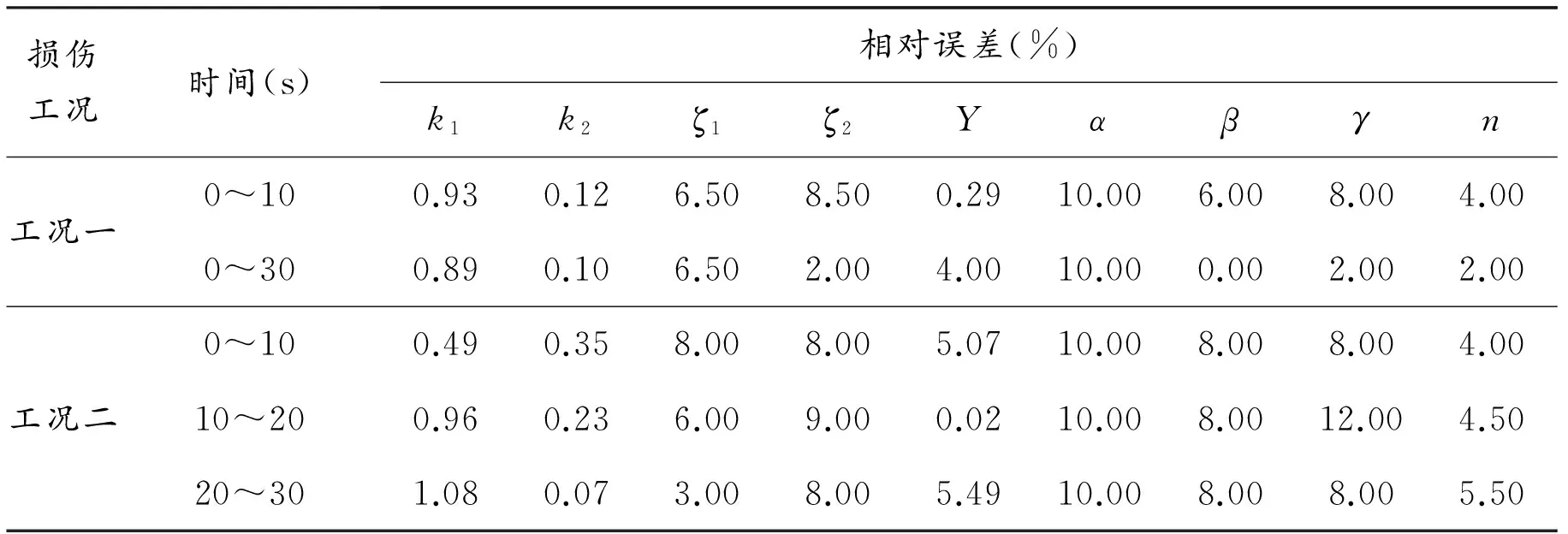
表2 IMPSCO参数辨识结果

从表2可以看出：各工况层间初始刚度(k)的辨识精度都较高，工况一和工况二的最大辨识误差分别为0.93%和1.08%，而其他参数的辨识精度相对较低。这是因为在利用时程响应建立适应度函数时，数值模型对响应的预测值主要是由结构刚度决定，受结构本身阻尼影响很小，此外Bouc-Wen模型参数主要决定结构的滞回特性，对结构响应的灵敏度较低。而在结构损伤识别中，通常是根据结构刚度的退化情况来诊断结构的损伤状态，因此即使阻尼比和Bouc-Wen模型参数的辨识精度较低，也不影响对结构损伤情况的正确判断。进一步根据结构参数辨识结果计算得到结构底层恢复力曲线的识别值，并与理论值进行对比，如图5所示。

从图5可以看出，尽管第II阶段结构阻尼比和Bouc-Wen模型参数的辨识精度较低，但各工况结构底层恢复力曲线的识别值均与实际值非常接近。这表明通过第II阶段的识别，不但能够准确诊断出时变非线性结构的损伤位置和程度，还能够成功识别出结构的非线性特征。

图5 底层恢复力曲线对比图

4 结论

本文提出的两阶段损伤识别策略对于时变非线性结构是可行的。通过第I阶段可以准确判断损伤发生的时刻并快速地初步定位损伤，接着通过第II阶段就可以进一步精确定位损伤并诊断损伤的程度，同时还能够成功地识别出结构的非线性特征。但该方法对于结构复杂以及外部激励未知的情况还需要进一步研究扩展，同时也需要通过试验研究来进一步检验。

[1] Fan W，Qiao P Z．Vibration-based damage identification methods：A review and comparative study[J]．Structural Health Monitoring，2011，10(1)：83-111．

[2] Yang J N，Lin S．On-line identification of nonlinear hysteretic structures using an adaptive tracking technique[J]．International Journal Non-Linear Mechanics，2004，39：1481-1491．

[3] 尹强，周丽．基于遗传优化最小二乘算法的结构损伤识别[J]．振动与冲击，2010，29(8)：155-159.

[4] Nayyerloo M, Chase J G, Macrae G A, et al. LMS-based approach to structural health monitoring of nonlinear hysteretic structures[J]. Structural Health Monitoring, 2011, 9(2):429-444.

[5] 黄致仁．具迟滞回复力折减之钢筋混凝土框架的系统识别[D]．台北：国立台湾大学，2009．

[6] Ye M Y ，Wang X D．Parameter estimation of the Bouc-Wen hysteresis model using particle swarm optimization[J]．Smart Materials and Structures，2007，16(12)：2341-2349．

[7] Charalampakis A E, Dimou C K．Identification of Bouc-Wen hysteretic systems using particle swarm optimization[J]．Computers and Structures．2010，(88)：1197-1205．

[8] Yang Y,Nagarajaiah S．Blind identification of damage in time-varying systems using independent component analysis with wavelet transform [J]. Mechanical Systems & Signal Processing, 2014, 47(12):3-20.

[9] Ma F，Zhang H，et al．Parameter Analysis of the Differential Model of Hysteresis．Journal of Applied Mechanics，2004，71(3)：342-349．

[10] 李爱国．多粒子群协同优化算法[J]．复旦大学学报：自然科学版，2004，43(5)：923-925．

[11] Jiang S F, Wu S Y, DONG L Q. A Time-Domain Structural Damage Detection Method Based on Improved Multi-particle Swarm Co-evolution Optimization Algorithm[J]. Mathematical Problems in Engineering, 2014, 44(1):77-85.

[12] Jiang S F, Ma S L. Structural Damage Detection Based on Improved Multi-Particle Swarm Co-Evolution Optimization Algorithm[M]//Structural Health Monitoring-Measurement Methods and Practical Applications, Dr. Moises Rivas-Lopez (Ed), InTech, 2017：47-64.

[13] 董利强．基于改进多粒子群协同优化与统计特征提取的智能损伤检测[D]. 福州：福州大学，2012．

Studyontwo-stagedamageidentificationoftime-varyingnonlinearstructures

WU Si-yao

(JinshanCollegeofFujianAgricultureandForestryUniversity,Fuzhou350108,China)

Using Bouc-Wen model to simulate the nonlinearity of structure, a two-stage damage identification strategy is proposed to detect the damage condition of time-varying nonlinear structures under the condition of stiffness mutation. In the first stage, we use wavelet-independent component Analysis (WT-ICA) technique to identify the catastrophe point, and then determine the time of the damage and locate the damage. In the second stage, the improved multi-particle swarm optimization algorithm (IMPSCO) with Bouc-Wen model is used to identify the parameters of time interval. Thus the precise location of damage and the degree of damage are determined. The feasibility and validity of the proposed method are validated by a numerical example. The results show that the proposed method can be applied to the damage assessment of time-varying nonlinear structures and can accurately identify the nonlinear characteristics of structures.

damage identification; Bouc-Wen model; wavelet singularity analysis; independent component analysis; particle swarm optimization

2017-07-25

国家语委“十二五”科研规划2014年度重点项目(ZDI123-23)

吴思瑶(1989—)，女，福建宁德人，工学硕士。

1674-7046(2017)05-0001-07

10.14140/j.cnki.hncjxb.2017.05.001

TP391.41

A