永磁同步电机模糊变阶次分数阶滑模控制研究*

崔磊，黄家才，施昕昕，赵涛

（南京工程学院 自动化学院，南京211167）

0 引 言

近年来，分数阶控制及其应用研究得到国内外学者的广泛重视。文献［1］研究了分数阶在橡胶坝流量控制中的应用；文献［2］将分数阶控制应用于制导弹箭系统中，提高了命中目标的准确度；文献［3］针对直流双闭环调速系统，研究并设计了分数阶控制器，提高了系统性能。文献［4］研究了直流调速系统模糊自整定分数阶内模控制，及其对频域性能的改善；文献［5-6］分别将分数阶控制应用在电液位置伺服系统和气动位置伺服系统中；文献［7-9］将分数阶控制与神经网络、模糊逻辑、粒子群算法相结合提出了相应的智能控制方法。文献［10-12］研究了分数阶滑模控制方法并应用于永磁同步电机控制系统中，提高了系统的鲁棒性和动态性能。

目前大多分数阶控制是基于常数阶次的，即在控制过程中阶次是恒定不变的。近年来，变阶次分数阶微积分的数值解以及变阶次分数阶控制引起了国内外学者的重视。文献［13］提出了基于切比雪夫多项式的数值实现方法；文献［14］提出了分数变阶次微分方程的求解方法；文献［15］讨论了动态建模中变阶次分数阶微积分算子的选择。

分数阶滑模控制器由于其鲁棒性强等优点而被广泛研究［10－12］，但目前滑模控制中分数阶次大多为常数。为了进一步提高分数阶滑模控制的全局控制性能，本文将常数阶次分数阶滑模控制拓展到变阶次（variable-orders）滑模控制，并以永磁同步电机速度控制为例，提出一种新的模糊变阶次分数阶滑模控制方法。文中首先基于PMSM的数学模型，设计了变阶次分数阶滑模速度控制器；然后通过分析不同阶次时分数阶滑模控制器的性能，获得了最优阶次的变化规律；最后构建了以速度误差为输入、阶次为输出的模糊推理规则，并设计了模糊变阶次分数阶滑模控制器。仿真结果证明所提方法在控制性能上优于常数阶次分数阶滑模控制方法。

1 常数阶次分数阶微积分

式中 下标a和t分别表示算子定义中的下限和上限；α是算子的阶次；R（α）是α的实部。一般来说α∈R，实际上 α可以是任意复数，且当 R（α）＞0时，表示分数阶微分运算；当 R（α）＜0时，表示分数阶积分运算。

分数阶微积分最常用的定义是Grunwald-Letnikov（GL）定义和 Riemann-Liouville（RL）定义以及 Caputo定义［16－19］。

2 变阶次分数阶微积分

变阶次分数阶微积分算子可以由常数阶次分数阶微积分算子直接拓展而来［20］。常用的变阶次分数阶微积分定义有如下几种。

2.1 RL定义下的变阶次分数阶微积分算子

当阶次 α时变即 α＝α（t）时，将 α（t）代入 RL定义的积分公式，则可以直接得到RL定义下的变阶次分数阶积分表达式如下［15，21］：

同理可得到RL定义下的变阶次分数阶微分表达式如下：式中0＜α（t）＜1。

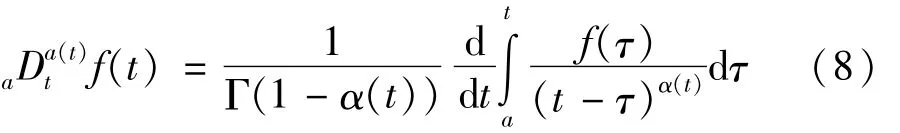
2.2 GL定义下的变阶次分数阶微积分算子

在实际工程应用中，系统采样时间为常数，由式（7）、式（8）给出的变阶次分数阶微积分算式计算复杂。为此，将α（t）代入GL定义，则可以得到GL定义下的时域变阶次分数阶微积分表达式如下［22］：

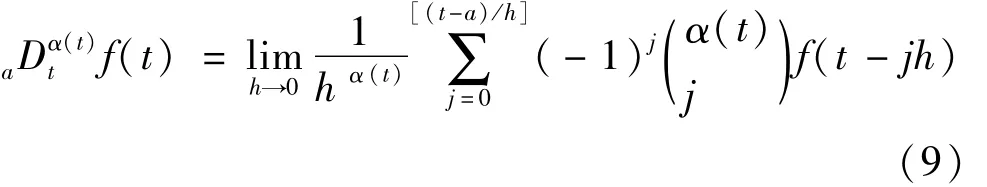
对于实时离散控制系统，假设其采样步长为CT，且系统从初始时刻开始计算，即a＝0，则式（9）可进一步写为：

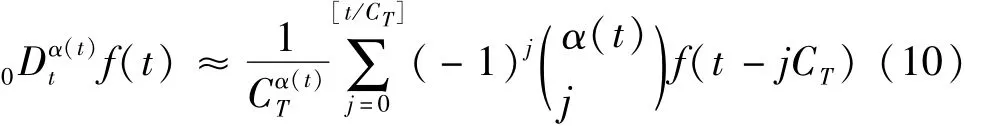
3 PMSM数学模型

为了得到PMSM的数学模型，作如下假设：a）忽略涡流效应和磁滞损耗；b）忽略磁饱和效应和转子的阻尼绕组；c）感应电动势为正弦波。在以上的假设下，基于d-q坐标系的PMSM的数学模型为［23］：

式中ud，uq分别代表d轴和q轴电压；id，iq分别代表轴d和q轴电流；Ld，Lq分别代表轴d和q轴电感；R为定子电阻；ω为电角速度；Ψf为永磁体的磁链。

PMSM电磁转矩表示为：

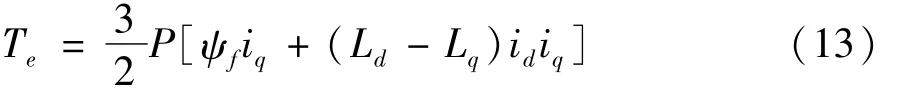
式中 Te为电磁转矩；为极对数；P对于表贴式PMSM，d轴电感等于 q轴电感，即Ld＝Lq，所以上述电磁转矩公式又可以表示为：

相应的机械方程表示为：

式中J为电机转动惯量；TL为负载转矩。

4 变阶次滑模控制器

4.1 系统控制框图

根据永磁同步电机在d－q旋转坐标系下的模型，构建永磁同步电机的速度矢量控制系统，控制框图如图1所示。采取SVPWM的调制方式，采用速度、电流双闭环控制策略，其中电流环采样频率10 kHz，采用PI控制器；速度环采样频率1 kHz，采用变阶次分数阶滑模控制器（VOFSMC）。

图1 PMSM变阶次分数阶滑模控制框图Fig.1 VOFSMC control block diagram for PMSM

4.2 VOFSMC设计

定义

其中ωref为速度给定值；ω为速度反馈值。设计变阶次分数阶滑模面如下：

式中 α（t）∈［0.1，1.9］，c1和 c2为大于零的系数，Dα（t）为分数阶微分算子。根据分数阶微积分的性质［17］，对 Svo求导可得：

由式（15）和式（16），x2和 x2可表示为：

采用指数趋近率，令：

式中ε和k为正系数，sgn（Svo）为符号函数，表示为：

将式（22）代入式（21），可得：

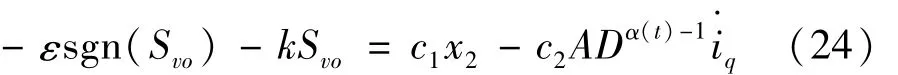
由式（24）可得：

则有：

4.3 VOFSMC稳定性分析

选择Lyapunov函数为：

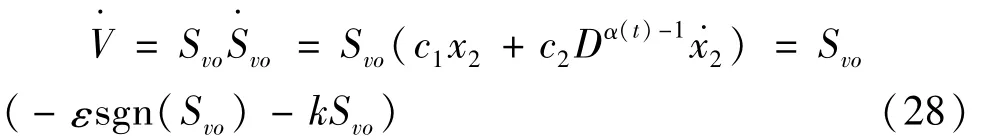
5 PMSM常数阶次分数阶滑模控制仿真实验

为了得到控制过程中最优阶次的变化规律，首先通过仿真实验分析不同阶次与控制性能的关系，从而得到最优阶次的变化规律，为变阶次分数阶滑模控制提供依据。实验中永磁同步电机参数为：额定转速为3 000 r/min，J＝0.425×10－3kg·m2，极对数 P＝4，Ψf＝0.081Wb，Rs＝0.985Ω，Ld＝Lq＝2.96 mH，B＝1.0×10－4N·m·s·rad－1，额定功率为PN＝600W，额定转矩为TN＝2 N·m。实验中，速度给定值为1 000 r/min，并记录系统超调量σ、调节时间ts、稳态误差e和施加负载时最大误eL差四组数据。在t＝0.2 s时施加5 Nm负载，在t＝3 s时取消负载。当阶次α分别取0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1.0、1.1、1.2、1.3时，可以获得不同的速度响应曲线，如图2和图3所示（图2和图3给出了部分阶次值时的速度响应曲线）。从速度响应曲线图中可以得到不同阶次时系统超调量σ、调节时间ts、稳态误差e和施加负载时的最大误差eL，如表1所示，其中当阶次α＜0.5以及α＞1.4时系统误差很大，因此表1中没有记录相应数据。

图2 阶次为0.6时的PMSM速度响应Fig.2 Velocity response of order 0.6 for PMSM

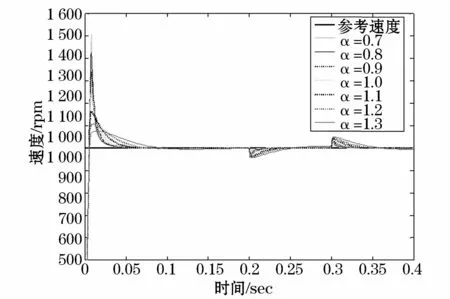
图3 阶次为0.7～1.3时的PMSM速度响应曲线Fig.3 Velocity response of order 0.7～1.3 for PMSM

当阶次取值范围α∈［0.6 1.3］时，对表1中的数据进行分析可以看出：（1）系统超调量σ随着阶次值的增大而逐渐减小；（2）系统调节时间ts随着阶次值的增大而逐渐增大；（3）当阶次值较大或者较小时，系统稳态误差e随着阶次值的增大或减小而逐渐增大，当阶次在α＝1附近时稳态误差最小；（4）当出现负载干扰时，系统负载误差随着阶次值的减少而逐渐降低。

表1 常数阶次时系统响应性能指标Tab.1 System response performance index of constant orders of simulation results

从上面分析可以看出，不同的分数阶次值对系统的性能指标影响不同，同时也说明固定不变的阶次值并不能使系统获得最佳的动态响应性能。为了获得综合最优性能指标，可以在控制过程中采取变阶次控制策略，这也是本文所提方法的出发点。

6 基于模糊逻辑推理的变阶次分数阶滑模控制

在系统运行过程中，以模糊数学为基础进行模糊逻辑推理，动态获得最优阶次，可以改善系统的整体控制性能。采用系统的误差e作为模糊输入量，阶次α（t）的取值作为模糊输出量，隶属度函数分别如图4和图5所示，模糊规则如表2所示。

图4 输入隶属度函数Fig.4 Inputmembership functions

表2 模糊规则表Tab.2 Fuzzy rule table

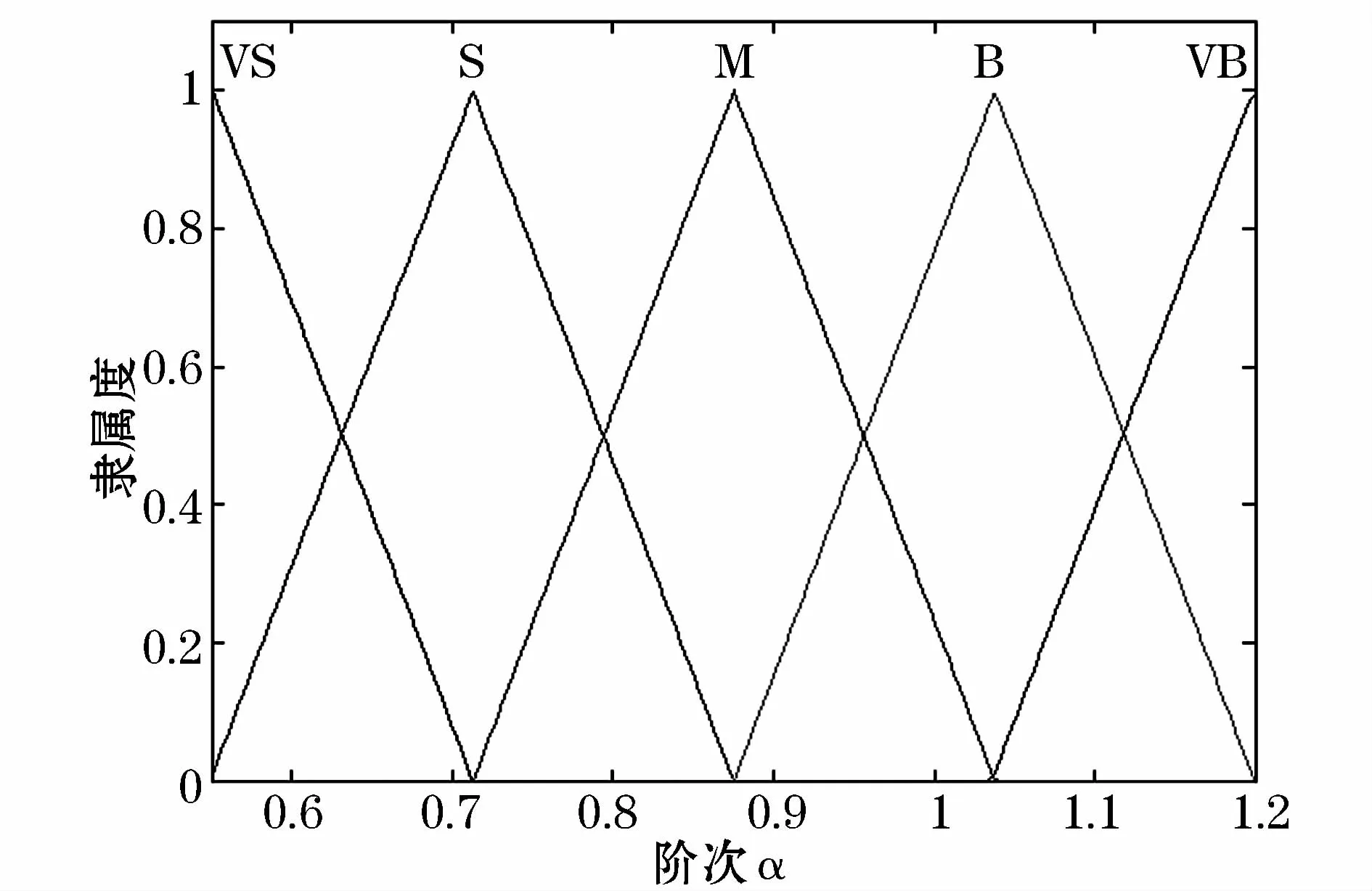
图5 输出隶属度函数Fig.5 Outputmembership functions

实验结果如图6～图8所示。其中图6为所提方法的速度响应曲线与固定阶次响应曲线的比较，图7为阶次α（t）的变化曲线，图8为速度误差曲线，表3为本文所提方法的控制性能参数。由图6所示，在系统启动阶段，阶次α（t）取较大的值，目的在于获得最小的超调量；在系统进入稳态后，阶次取较小的值，因此对负载扰动具有最好的抑制能力。在负载扰动导致速度有较大偏差后，阶次α（t）先变大，然后逐渐变小，以减少稳态误差。从表3可以看出，所提控制方法的系统超调很小，且抗负载能力优于常数阶次分数阶滑模控制方法。上述分析表明，本文所提出的模糊变阶次分数阶滑模控制方法具有较好的鲁棒性、快速性和准确性，具有较好的全局控制性能，这也证明了本方法的有效性。

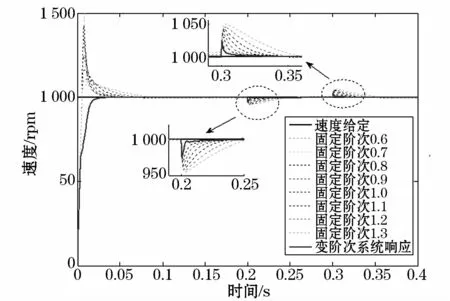
图6 本文方法的速度响应Fig.6 Velocity response of proposed method

图7 阶次的变化值Fig.7 Changes in the value of the order

图8 速度误差曲线Fig.8 Speed error curve

表3 本文所提方法的控制性能参数Tab.3 Control performance parameters of the proposed method

7 结束语

为了进一步提高分数阶滑模控制的全局控制性能，本文提出一种新的模糊变阶次分数阶滑模控制方法。文中通过分析不同阶次时分数阶滑模控制器的性能，获得了最优阶次的变化规律，并据此建立了以速度误差为输入、阶次为输出的模糊推理规则，最终设计了模糊变阶次分数阶滑模控制器。仿真结果证明所提方法具有较好的鲁棒性、快速性和准确性，在控制性能上优于常数阶次分数阶滑模控制方法，具有较好的全局性能指标。

本文所提出的模糊变阶次的控制想法，同样适用于其他分数阶控制方法。