用于通信系统的干扰对消电路设计与实现*
2017-12-20
(中国西南电子技术研究所,成都 610036)
用于通信系统的干扰对消电路设计与实现*
赖剑强**
(中国西南电子技术研究所,成都 610036)
针对通信设备应用的复杂化和对在复杂电磁环境下工作的设备电磁兼容性提出的更高要求,通过分析对消技术的基本原理,提出了一种模拟电路和数字电路相结合的干扰对消技术,并研制出了基于该技术的干扰对消原理样机。对该样机的单机测试和系统联试结果表明,该对消技术具备点频干扰和噪声干扰的抑制能力,对消收敛时间小于100 ms,对消比大于43 dB,适合在窄带通信中应用并可推广到其他领域。该成果正逐步在实际工程中得到运用。
通信系统;对消技术;干扰噪声;对消比
1 引 言
随着电子装备在各个工程领域的多样化、复杂化,各个设备工作带来的电磁兼容问题愈发凸显,特别是在复杂电磁环境中,需要在高灵敏度下工作的系统,例如远距离无线通信系统、雷达、微弱信号探测器等特别容易受到与有用信号在频谱上重叠的电磁噪声干扰,该干扰可能来自外界,也可能来自自身平台。
常规无线通信系统接收和发射不在同一频段或者两者在时间上不交叠,以避免发射对接收造成影响,显然这种系统的频谱利用率不高,业务量受到限制。如果能够解决本机发射对接收的干扰,就能实现同时同频的全双工通信,理论上可以将业务传输效率提高一倍[1-3]。
基于软件定义无线电(Software Defined Radio,SDR)发展起来的认知无线电(Cognitive Radio,CR)技术,由于不能对通信频带进行严格限制,射频前端不再需要包含射频滤波器、多级低噪放、混频器、低通滤波等复杂而稳定性又不太高的模拟射频电路,取而代之的是对接收信号进行简单放大后直接射频采样,在数字域完成所有的处理功能[4]。然而需要考虑的一个关键问题是接收信号的模数(Analog to Digital,AD)转换器件必须具有高采样率、高动态范围。通常天线会接收到包含多种强度多种频谱的混合信号,在这种环境下要求高动态范围,就需要使用主动对消技术抑制不需要的信号,然后再进行AD转换。
以上三种情况分别是常规系统间电磁干扰问题、系统应用扩展问题、新技术发展问题,这几种情况归结在一起都涉及到信号去干扰问题。对消技术用于解决干扰信号与有用信号在电磁频谱上有重叠的消除干扰问题,而这种干扰通常使用常规滤波等手段是无法实现的。将去干扰问题从干扰信号和有用信号两个方面看,很容易想到两种不同的解决思路:一种是根据事先知道的有用信号的部分信息,直接从混合信号中提取有用信号的完整信息或需要的信息,而不用关心干扰信号的情况,称为信号提取技术;另一种是通过某种途径得到与干扰信号等幅反相的信号并与原信号进行叠加合成,将不需要的干扰信号抵消掉,剩下的便是有用信号,这种方法关心的重点是干扰信号的特性及其消除方法,称为干扰对消技术。两种信号分离技术的目的相同而采用的手段和研究的对象则完全不同。
通过采集与进入通信接收信道中干扰信号的同源信号,然后对其进行幅度和相位的调整,与混入有用信号中的干扰信号进行叠加合成,在理论上可以抑制有用信号中的干扰信号且不对有用信号产生明显影响或带来新的干扰,这就是干扰对消技术的基础框架。干扰对消技术是抗干扰技术的一个分支,通常用于与有用信号同频或同址干扰的场景,是在不能通过滤波等简单手段达到抑制干扰的情况下,诞生的一种抗干扰技术。干扰对消技术经历了较长时间的研究,但由于其技术难度较大,在实际工程应用偏少,目前的研究和应用在通信、雷达等领域相对较多[5-10]。
基于国防装备和民用工业对对消的应用需求,本文研究了一种射频干扰对消技术,从理论上解释电磁对消现象并从对消基本原理入手,研究并设计了对消电路及基于该电路的原理样机,对样机进行了测试,得出了具有实际应用价值的结果,可为对消技术的后续研究和产品化提供指导。
2 对消技术基本原理
对消的概念在射频研究领域可解释为两个幅度相等、相位相差180°的电磁信号相互叠加合成,叠加后的结果为两个信号相互湮没,其能量以其他形式耗散掉,从而达到消除信号的目的。这里的叠加实际上是两组电磁波中方向相反的电场分量和磁场分量各自相互抵消的过程。在自由空间中,电磁波具有相互垂直的电场分量和磁场分量,它们位于垂直于传播方向的平面内。图1给出了理想介质中幅度相等、相位反相的两均匀平面波的电场分量和磁场分量,当它们在空间上相遇,会产生两者电场和磁场的重合,其表现形式就是电场分量及磁场分量均相互抵消,对外不再显示出两个对消信号频率电磁波的特性,通常转换为热量或其他形式的能量耗散掉。

图1 两均匀平面波电场及磁场相互抵消示意图Fig.1 Cancelling of the electric field and magnetic field in two uniform plane waves
对消技术主要有两种方式:一种是模拟对消,即通过对干扰信号进行采样,然后对采样信号进行射频调整,将调整后的信号与混入通信系统中的干扰信号进行对消;另外一种是数字对消,即数字信号处理的方式,通过对采样的干扰信号进行特征分析,然后经数字信号处理的过程消除通信系统中的干扰信号。考虑到工程运用的实际情况和技术难度,对消的应用前期采用模拟对消的方案较多;当今由于可编程器件的发展及滤波器相关算法的成熟,数字对消技术在其应用灵活性能、可靠性、硬件体积等方面逐渐显示出其强大的优势。
对消的性能指标衡量方法通常有三种[11]:
对消比——考核被对消信号(一般为干扰信号)在对消实施前后的削弱程度,用dB表示,它是一个相对值。一般具有实用价值的对消系统要求对消比达到20 dB以上。
对消残余——考核实施对消后干扰信号的强弱,用dBm或dBm/Hz表示,它是一个绝对值。对于不同的应用需求,根据有用信号的强弱,对消残余的要求差异较大。
系统处理增益——考核实施对消前后,系统输出端的信噪比与输入端信噪比的比值,用dB表示,表示对消电路对信噪比的改善程度。
这三种对对消效果的评价在本质上是一致的,只是关心的重点不同而已。
在实际情况下,两个相互对消的射频信号无法完全满足幅度相等、相位相差180°的理想条件,总会存在一定的幅度和相位偏差,这种偏差会带来对消不完全,造成对消残余,也就存在对消比的概念。假设当上述幅度偏差为ΔA,相位偏差为ΔP,则射频对消比CR可表示为
(1)
通过上述表达式可得到如图2所示的几种典型对消比情况下幅度偏差和相位偏差的关系曲线。由图可见,在对消比要求不高的情况下,对消信号与被对消信号的幅度和相位偏差要求较为宽松;但当需要较高的对消比时,则对信号的偏差要求特别严格,如图中给出的当对消比要求为50 dB时,幅度偏差要求控制在0.027 5 dB以内,相位偏差要求控制在0.181 2°以内,如此高的精度已经超出常规测试仪器的测量误差,这也是对消电路设计的难点所在。

图2 对消比与幅度偏差和相位偏差的关系Fig.2 The relationship between cancel ratio and amplitude deviation & phase deviation
为了对射频对消效果进行直观评价,通常采用以下方式来定义对消比:
(2)
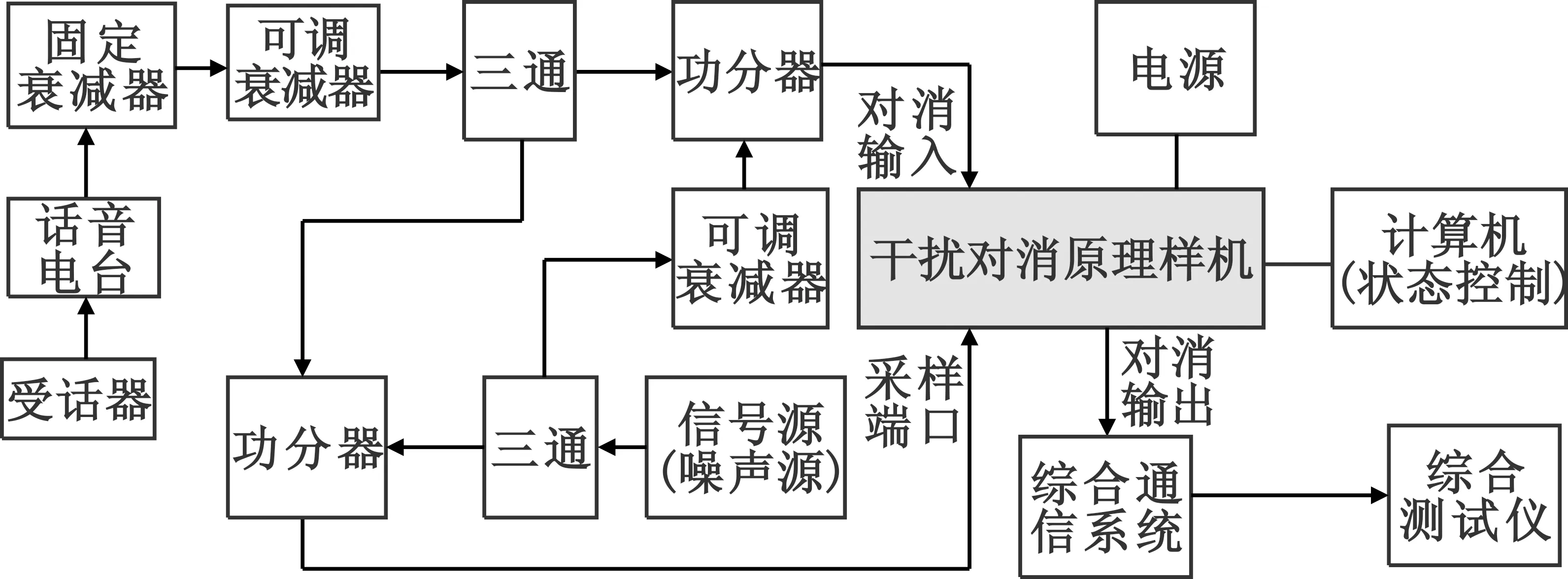
式中:Pi、Pr分别表示输入的被对消信号功率和对消完成后输出的残余信号功率,均以W为单位表示,在有效对消的情况下Pr 对于一个高对消比的系统,由于电路工作带来的自身温度变化、外界环境变化、器件老化衰退等引起的电路参数的少许漂移足以引起对消效果的严重恶化,所以通常情况下要求对消系统能够进行自动控制,构成自适应系统。最典型的方法是采用负反馈回路,电路可以根据对消结果实时调整电路参数,以长时间稳定保持良好对消效果。 对消电路的任务是根据被对消信号(干扰信号)的特征信息生成对消信号,并对两个信号进行叠加,以消除或降低被对消信号的强度,同时不带入新的干扰信号,以达到将进入系统的干扰抑制到规定要求的目的。对消信号可以由对消电路自己携带的信号源产生,也可以是通过采样被对消信号的同源信号经调整后产生,如果条件许可,一般以第二种方式设计电路更为方便。图3给出了一个用于消除无线接收机中干扰信号的同源干扰对消系统,其中的核心部分为对消信号生成电路,可以是模拟电路、数字电路或者两者的结合。 图3 典型的同源干扰对消系统Fig.3 A tipycal homologous interference cancellation system 模拟射频对消的基本原理可用图4框图表示。干扰信号由干扰源发射后其部分Ti经某种途径混入通信信号S中,采集部分干扰信号Tc引出一条支路对其做幅度和相位调整,然后将调整后的信号Tc′与混有干扰信号的通信信号S+Ti进行叠加合成。由于合成后的信号中既有通信信号S又包含了由于对消不完全的残余信号r,所以可对该信号进行取样并进行相关检测。为了只检测残余信号而忽略有用信号,需要引入原始干扰信号作为信号检测的本振源Tl,检测结果作为幅/相调整的依据。这样就建立了一个能够自适应调整电路参数的负反馈环路,最终使得残余信号足够小,得到较为纯净的通信信号。由于幅/相调整电路可以根据对残余信号检测结果作实时调整,该电路可以长时间保持稳定的对消比。 图4 模拟射频对消原理框图Fig.4 Functional diagram of analog RF cancellation 原理框图中核心部分为由幅相调整器、对消合成器、相关检测器和自适应控制电路构成的负反馈环路。信号检测的准确度决定了幅/相调整控制信号的准确度,从而也就决定了输出残余信号的强弱,即决定对消比的关键。为了驱动整个系统的运行,控制电路中驻入了自适应对消控制算法,并可根据实际应用的需求进行算法调整,确保系统准确高效工作。相关检测和幅/相调整的性能是算法准确收敛的保证,任何一者出现问题或准确度不够将会导致虚假收敛或长时间无法收敛。从图中可以看到,决定对消效果的因素有相关检测精度、控制精度以及幅/相调整精度。 相比于模拟电路,数字对消电路的特点在于使用了数字自适应滤波器技术,对消信号的调整在数字域完成,避免了模拟电路稳定性差、电路形式复杂、体积重量大等缺点,而主要的工作转移到了自适应滤波器及其算法性能上了。前人的研究认为,如果噪声信号是一个广义平稳随机过程,则自适应滤波器可以采用横向滤波器实现[12]。图5是一个采用横向自适应滤波器的数字对消电路原理框图。 图5 数字对消原理框图Fig.5 Functional diagram of digital cancellation 最小均方(Least Mean Square,LMS)算法由于其结构简单、不需要计算相关函数、不需要对矩阵求逆运算等优点适用作为图5所示的滤波器算法。该算法属于随机梯度算法中的一种。LMS算法作为线性自适应滤波算法,主要包括两个过程:一是滤波过程,计算线性滤波器输出信号对输入信号的响应,比较输出结果与期望响应得到误差估计;二是自适应过程,根据误差估计自动调整滤波器控制参数。实际上这两个过程构成了一个反馈环路,使得自适应过程得以实现。 一个M阶的横向滤波器结构如图6所示,输入向量被逐级延时单元分成M组信号元素,每组信号对应一个权值元素,所有权值元素构成一个M阶抽头权值向量。所有的参数都可以通过矩阵的形式表达,经LMS算法迭代计算后得到一个对期望信号的估计,当迭代足够多次后,对于广义平稳随机过程,得到的估计可以看作该过程的维纳解。在一个较短暂的时间内,通信系统的干扰信号可以看作广义平稳随机过程。 图6 M阶横向滤波器结构Fig.6 Structure of M-order transversal filter 在滤波器运行过程中,期望信号作为判断滤波器输出的标准必须参与运算,主要目的是得到滤波输出的误差信号,以作为权值向量的控制参考。 运用最小均方自适应算法,可以得到抽头权值向量的迭代方程的复数形式为 w(n+1)=w(n)+2ηu(n)e*(n)。 (7) 式中:e*(n)=d(n)-wH(n)u(n),wH(n)表示转置共轭。迭代开始时抽头权值向量定义了一组猜测初始值w(0),如果有先验值则使用先验值作为初始值,没有则用全0作为初始值。方程等式右边第二项代表了本次迭代对抽头权值向量w(n)估计的调整,η为步进因子,它决定了自适应迭代过程的速度。步进因子越大自适应过程的速度越块,但算法得到的稳态解与维纳解的差别越大,可导致算法的失调。因此,对η的选择需要综合考虑算法的稳定收敛与计算时间的消耗。图7给出了使用最小均方算法得到的一个受噪声污染的周期为1/3、幅值为1的正弦波信号的去噪结果。其中滤波器为128阶,离散信号长度为10 150,步进因子为0.001 5,噪声干扰信号为高斯白噪声序列(标准正态分布的伪随机序列),抽头权值向量用全0作为初始计算值。 (a)期望信号 (b)含噪信号 (c)滤波输出 (d)误差强度图7 采用最小均方算法滤波计算结果Fig.7 Filtered result based on minimum mean square algorithm 由计算结果可知,自适应滤波器很好地抑制了信号中的噪声干扰,去噪后的信号中起伏比较大的地方表明误差信号较为剧烈,这与算法的步进因子、迭代次数及滤波器阶数均相关。由于每次计算的噪声信号为伪随机数,所以各次计算的结果均不相同,误差强度直接体现了计算结果的好坏。通过多次计算后统计发现,随着迭代次数的增加误差强度会呈现出近似周期性的极大值,这也反映了计算的自适应过程。 对于一个对消系统,对消比越高则要求的残余信号越小,对相关检测的精度要求就越高,对消算法的收敛门限设置就得足够严格,同时就会带来反馈回路更难收敛,循环运算次数越多,时间消耗也就越大,并且在对消完成后由于外界条件和内部器件参数变化导致触发系统重启反馈运算的概率也就越大。因此,在工程应用中应该根据实际的需求,在对消比和资源消耗上权衡考虑。 前文分析的模拟对消电路和数字对消电路是两种实现干扰对消的技术途径,各有其技术特点。模拟对消电路原理简单,技术难度较小,电路实现容易,但在稳定性上有一定的缺点,为了克服电路间干扰以实现精确收敛,往往功能电路体积重量较大。数字电路的核心电路采用常用的集成可编程芯片(如FPGA或DSP)为基础,通过软件在数字域进行计算,处理方式灵活多变,在芯片硬件资源足够的情况下,对消电路的性能主要体现在软件能力上,往往对硬件的依赖程度很小,这也可缩短开发周期,便于调试优化,但数字对消电路在射频前端AD转换的动态范围要求较高,实现有一定难度。 为了克服两种对消电路的缺点,我们研究了一种数模混合对消电路,该电路以图4所示的模拟电路为构架,在负反馈的运算及对对消信号调整量的控制上采用数字控制的方式。图8是控制电路的结构框图,其中FPGA接收来自相关检测器的反馈信号,并将该反馈信号送入DSP作为算法运算的依据,DSP运算收敛后将结果通过FPGA送给幅/相调整器,实现对对消信号的调整。 图8 对消控制电路结构Fig.8 Control circuit of canceller 整个对消电路工作在超短波频段的一定带宽内,电路以点频的方式工作,针对常规窄带通信模式的干扰消除特别有效。对于跳频等抗干扰通信模式,对对消系统的运算时间要求较为严格,一般只要对消收敛算法的时间小于每一跳的稳定时间的1/10,例如一个500 hop/s的通信模式,则要求每一个频点收敛时间在0.2 ms以内,这需要硬件具有高速计算能力以及算法的高运行效率的支持。 我们对研制的干扰对消原理样机进行了实验室测试,通过信号源发射单载波信号以及发射加性高斯白噪声(Additive White Gaussian Noise,AWGN)信号两种情况,以某超短波频点f1为例,得到的测试结果如图9 所示。图9(a)、(b)是以干扰信号为单载波时进行射频对消的结果,干扰信号强度由-10.4 dBm被对消到了-75.8 dBm,对消比达到了65.4 dB;图9(c)、(d)是以干扰信号为加性高斯白噪声时进行射频对消的结果,在对消前,噪声功率谱密度为-101.7 dBm/Hz,对消运行后,噪声信号被削弱到了-160.6 dBm/Hz,对消比达到了58.9 dB。通过计算机监测对消算法开始到对消稳定后的时间差,多次测试得到对消收敛时间在48~93 ms之间。 (a)单载波对消前的信号强度 (b)单载波对消后的信号强度 (c)噪声对消前的功率谱密度 (d)噪声对消后的功率谱密度 基于以上测试结果,将该干扰对消原理样机在某机载平台综合通信系统上进行了验证性测试,测试框图如图 10所示。测试系统中各个支路衰减器衰减量以及噪声源输出信号强度均来源于该机载平台的实际参数。为了尽可能模拟真实环境,在采样端口将有用信号叠加在噪声信号中。测试中,将AM或FM话音信号与AWGN干扰信号混合,然后经过干扰对消样机,再送入综合通信系统,在干扰对消原理样机工作和不工作的情况下,调节射频话音信号输入强度,保持不同情况下通信系统输出话音信号信纳比为固定值10。干扰对消工作和不工作时,在达到相同的输出信纳比情况下,射频话音信号的强度差可间接视作原理样机的对消能力,即对消比。 图10 干扰对消原理样机在通信系统中测试框图Fig.10 Test diagram of the interference cancellation principle prototype in a communication system 在设备可工作频带范围内随机抽取了典型代表点进行测试,测试中保证话音电台发射的话音信号的载波与噪声源发射的具有一定带宽的AWGN信号在频谱上是重合的。在抽取的6个代表频点中,测试得到对消比最大值为46 dB,最小值为43 dB。这与单机测试的结果有一定差距,主要原因是由于测试环境本身引入的额外干扰,而干扰对消样机尚不具备处理外加不可预知的干扰信号的能力,这也是该项技术以后需要改进的方向。 根据射频对消的基本原理,本文对干扰对消电路进行了研究,分析了模拟和数字两类电路的特点,设计并研制出了一种数模混合的对消原理样机,对其进行了单机测试和综合通信系统联机验证测试,到了如下结果:对消电路具备点频干扰和噪声干扰抑制的能力;对消收敛时间较短,普遍可控制在100 ms以内;噪声干扰对消比达到43 dB以上,具有较好的对消能力。测试结果验证了本文研究的干扰对消电路的正确性和有效性,在通信系统中具有较高的应用价值,能显著提高电磁噪声干扰情况下的接收机性能。样机的收敛时间在数十ms量级,适合常规模式窄带通信应用,但对于高速跳频等抗干扰通信模式,还需要进一步缩短收敛时间。该技术不仅适用于通信系统,在电子对抗、信号探测、雷达、医疗检测等领域均具有普遍借鉴意义和潜在应用价值。 [1] ELSAYED A,ELTAWIL A M,SABHARWAL A. Rate gain region and design tradeoffs for full-Duplex wireless communications[J].IEEE Transactions on Wireless Communications,2013,12(7):3556-3565. [2] 王俊,赵宏志,卿朝进,等.同时同频全双工场景中的射频域自适应干扰抵消[J].电子与信息学报,2014,36(6):1435-1440. WANG Jun,ZHAO Hongzhi,QING Chaojin,et al.Adaptive self-interference cancellation at RF domain in co-frequency co-time full duplex systems[J].Journal of Electronics & Information Technology,2014,36(6):1435-1440. (in Chinese) [3] PHUNGAMNGERN N,UTHANSAKUL P,UTHANSAKUL M. Digital and RF interference cancellation for single-channel full-duplex transceiver using a signal antenna[C]//Proceedings of International Conference on 10th Electrical Engineering/Electronics,Computer,Telecommunications and Information Technology (ECTI-CON). Krabi,Thailand:IEEE,2013:1-5. [4] SEAN H,THO L N. MIMO full-duplex precoding:a joint beam forming and self-interference cancellation structure[J].IEEE Transactions on Wireless Communications,2015,14(4):2205-2217. [5] SVILEN D. Iterative cancellation of non-linear distortion noise in digital communication systems[J].IEEE Transactions on Communications,2015,63(6):2325-2336. [6] 袁杰. 射频干扰对消技术在通信系统集成中的应用[J].电讯技术,2012,52(12):1870-1875. YUAN Jie. Application of RF interference cancellation technology in communication system integration[J].Telecommunication Engineering,2012,52(12):1870-1875. (in Chinese) [7] 王云阵. 自干扰抵消技术和接收机线性化的研究及其在超高频RFID中的应用[D].合肥:中国科学技术大学,2016. WANG Yunzhen. Research of self-interference cancellation technique and linearization for receiver and its application in UHF RFID[D].Hefei:University of Science and Technology of China,2016.(in Chinese) [8] 高鑫,何方敏,孟进,等.宽带干扰信号消除分析[J].通信技术,2016,49(8):975-979. GAO Xin,HE Fangmin,MENG Jin,et al.Analysis on wideband interfering signal cancellation[J].Communication Technology,2016,49(8):975-979. (in Chinese) [9] 王宝平. 线性调频连续波雷达信号泄漏对消技术的研究[D].成都:电子科技大学,2013. WANG Baoping. Research of FMCW radar leakage signal cancellation Technology[D].Chengdu:University of Electronic Science and Technology of China,2013. (in Chinese) [10] 蒋云昊,赵治华. 参考信号耦合有用信号对干扰对消系统的影响及其抑制[J].通信学报,2015,36(9):98-108. JIANG Yunhao,ZHAO Zhihua. Infuence and its suppression of desired signal coupling to reference signal to interference cancellation system[J].Journal on Communication,2015,36(9):98-108.(in Chinese) [11] LI W L,ZHAO Z,TANG J,et al.Performance analysis and optimal design of adaptive interference cancellation system[J].IEEE Transactions on Electromagnetic Compatibility,2013,55(6):1068-1075. [12] HAYKIN S. 自适应滤波器原理[M].郑宝玉,译. 4版.北京:电子工业出版社,2010:3-23. DesignandImplementationofInterferenceCancellationCircuitforCommunicationSystems LAI Jianqiang (Southwest China Institute of Electronic Technology,Chengdu 610036,China) For the increasingly complicated applications of communication system and higher electromagnetic compatibility requirements for equipment under complex electromagnetic environment,an interference cancellation technology based on the mixed analog and digital circuit is proposed. After the principle analysis,an elementary prototype for interference cancellation is developed and tested. The corresponding experimental results indicate that point frequency and noise interference can be suppressed with a convergence time less than 100 ms and a cancellation ratio greater than 43 dB. The cancellation technology is suitable for narrowband communications and also worth spreading to other areas. It has been applied in practical engineering. communication system;cancellation technology;interference noise;cancellation ratio 10.3969/j.issn.1001-893x.2017.12.012 赖剑强.用于通信系统的干扰对消电路设计与实现[J].电讯技术,2017,57(12):1415-1421.[LAI Jianqiang.Design and implementation of interference cancellation circuit for communication systems[J].Telecommunication Engineering,2017,57(12):1415-1421.] 2017-08-14; 2017-10-23 date:2017-08-14;Revised date:2017-10-23 LJQ6601@foxmail.comCorrespondingauthorLJQ6601@foxmail.com TN973 A 1001-893X(2017)12-1415-07 赖剑强(1982—),男,四川成都人,2012年获工学博士学位,现为工程师,主要研究方向为航空电子及无线通信技术。 Email:LJQ6601@foxmail.com3 对消电路形式

3.1 模拟对消电路
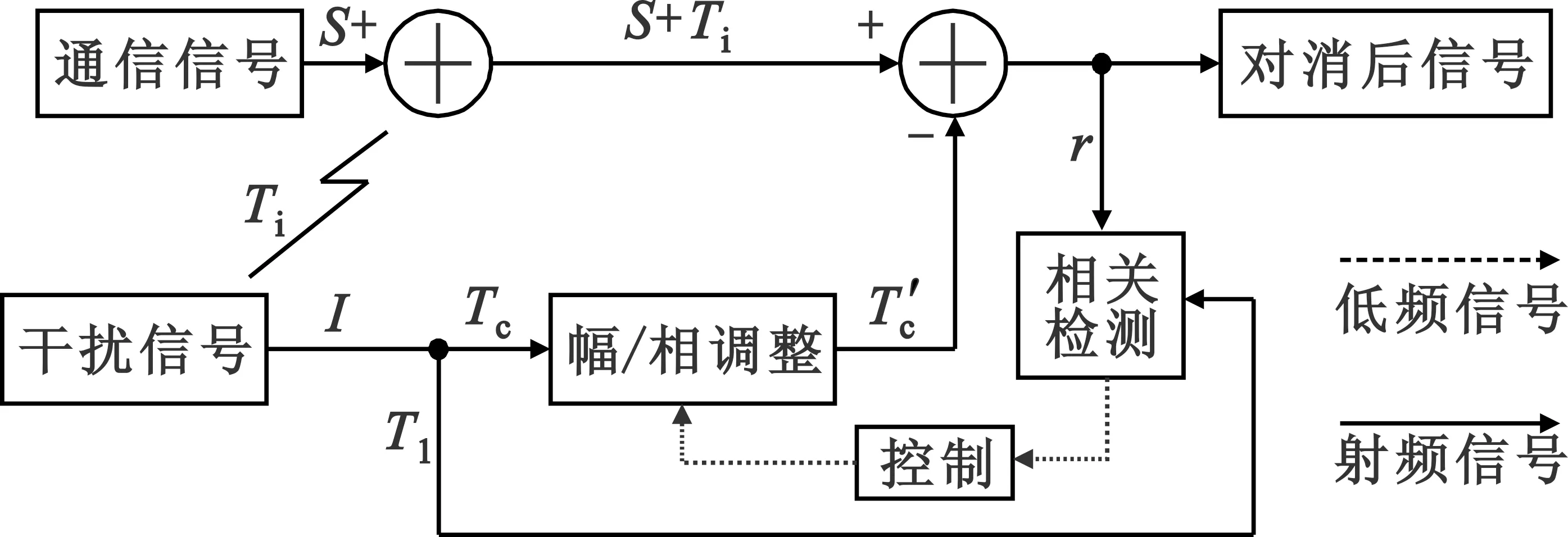
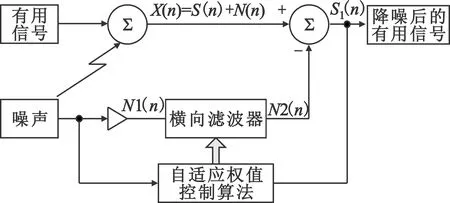
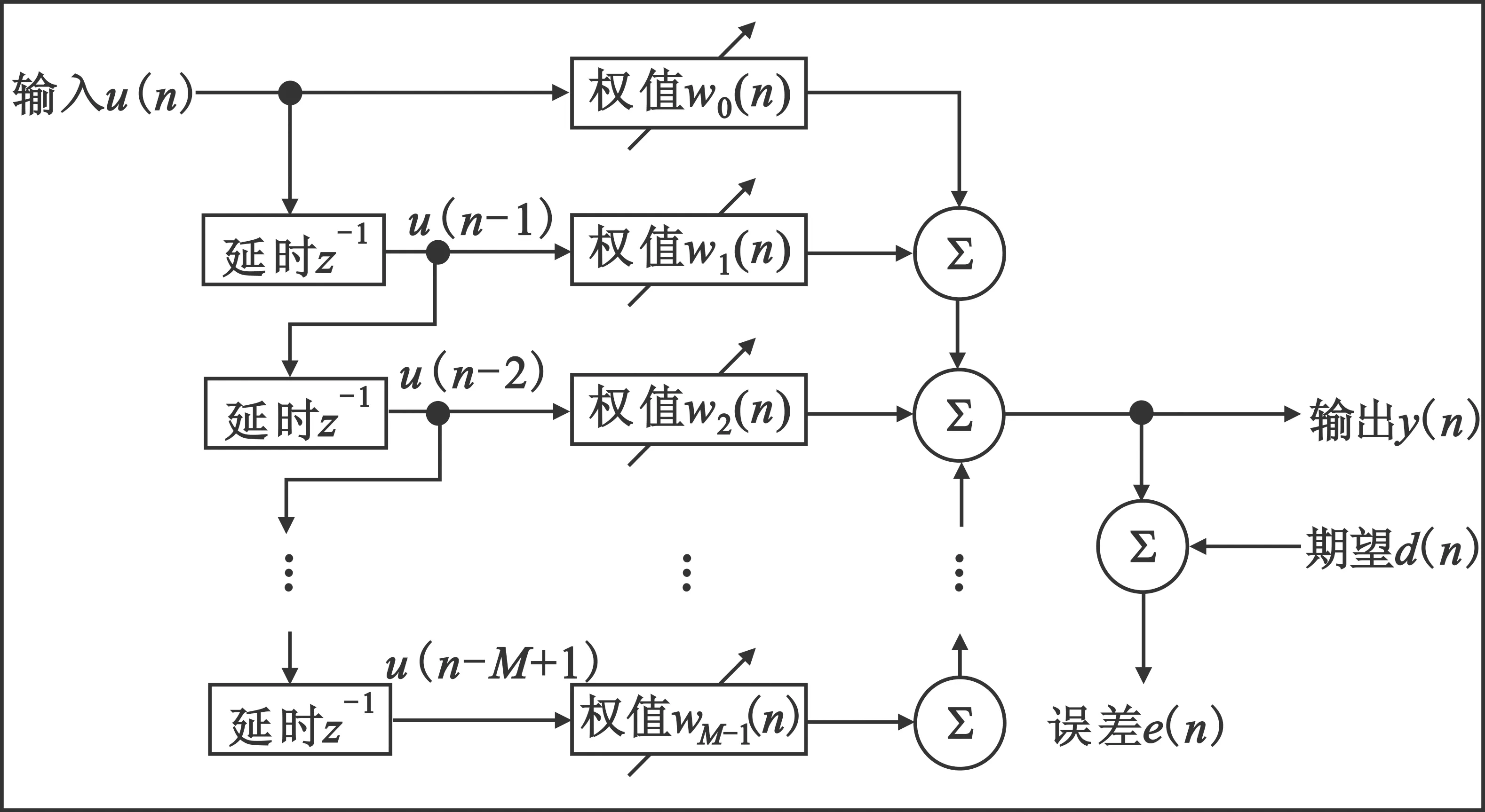
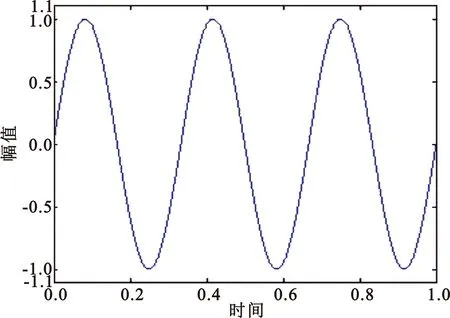
3.2 数字对消电路


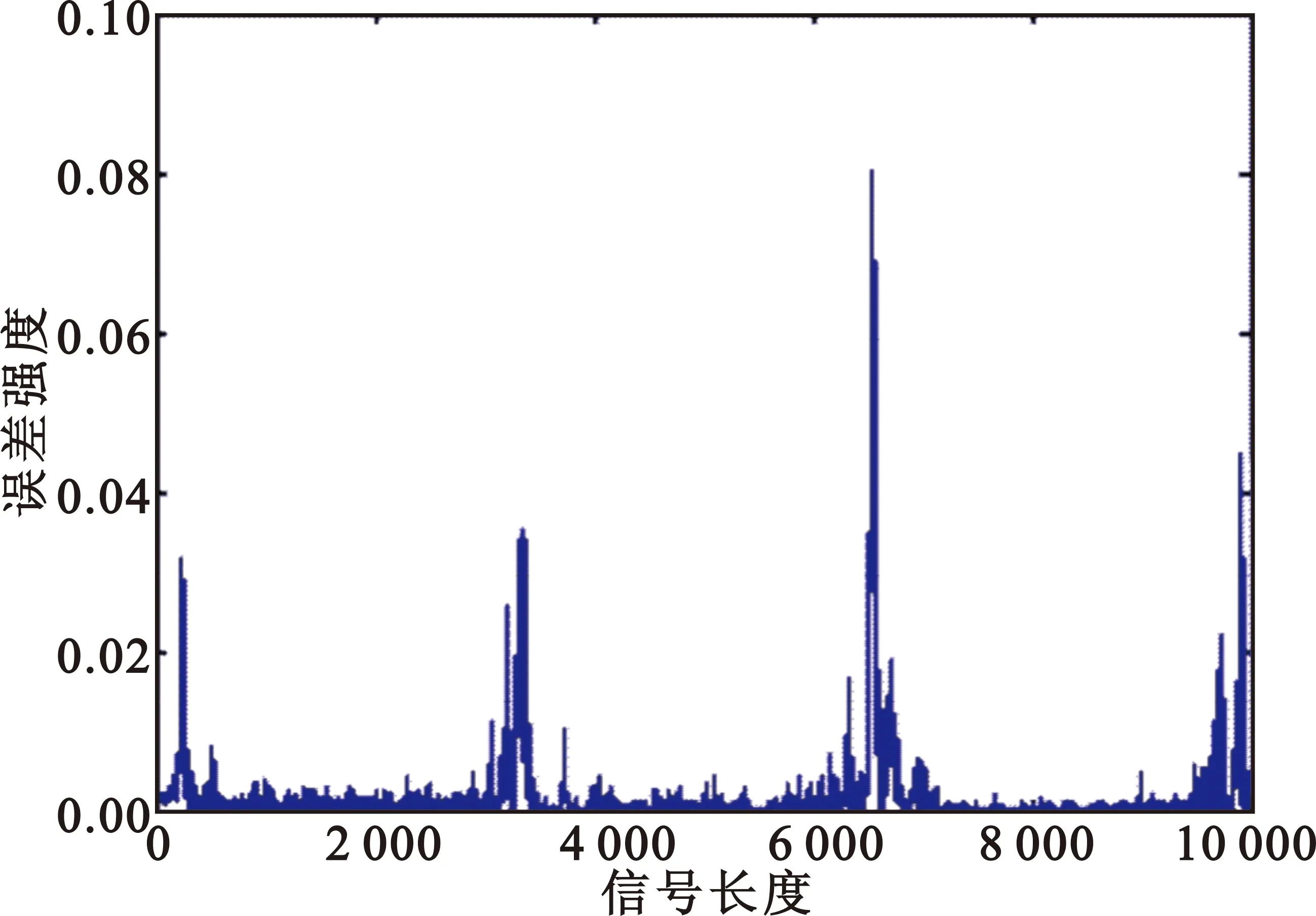
4 原理样机测试
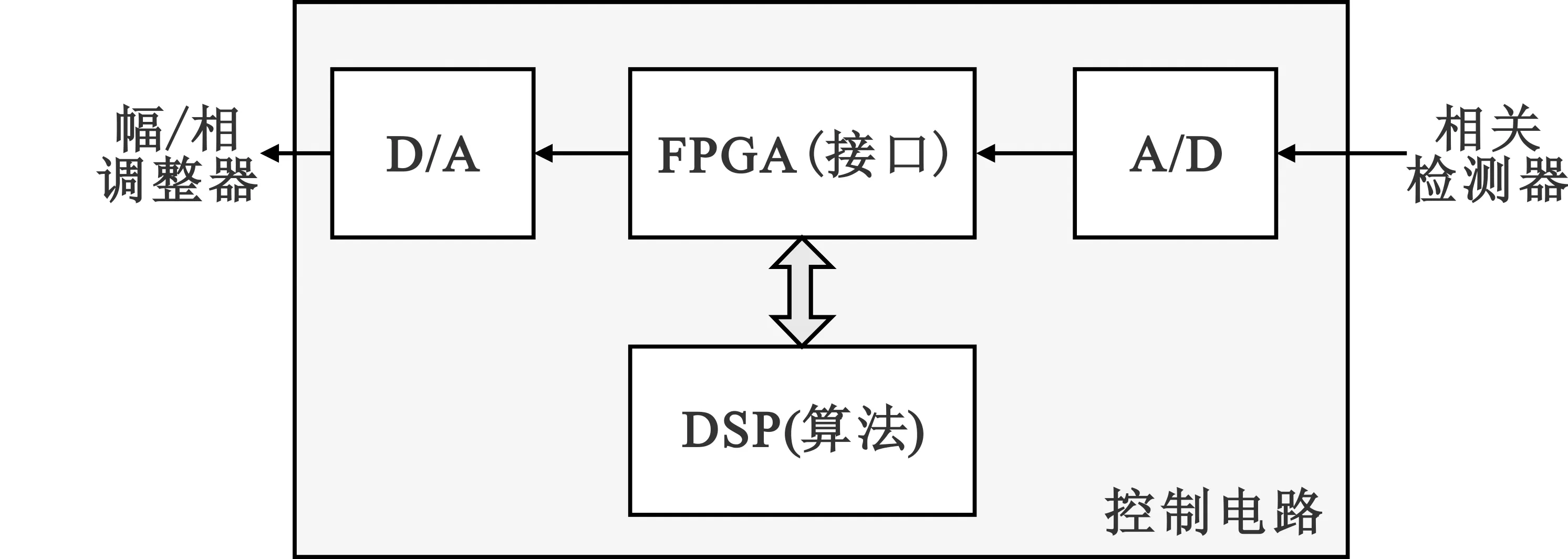
4.1 单机测试
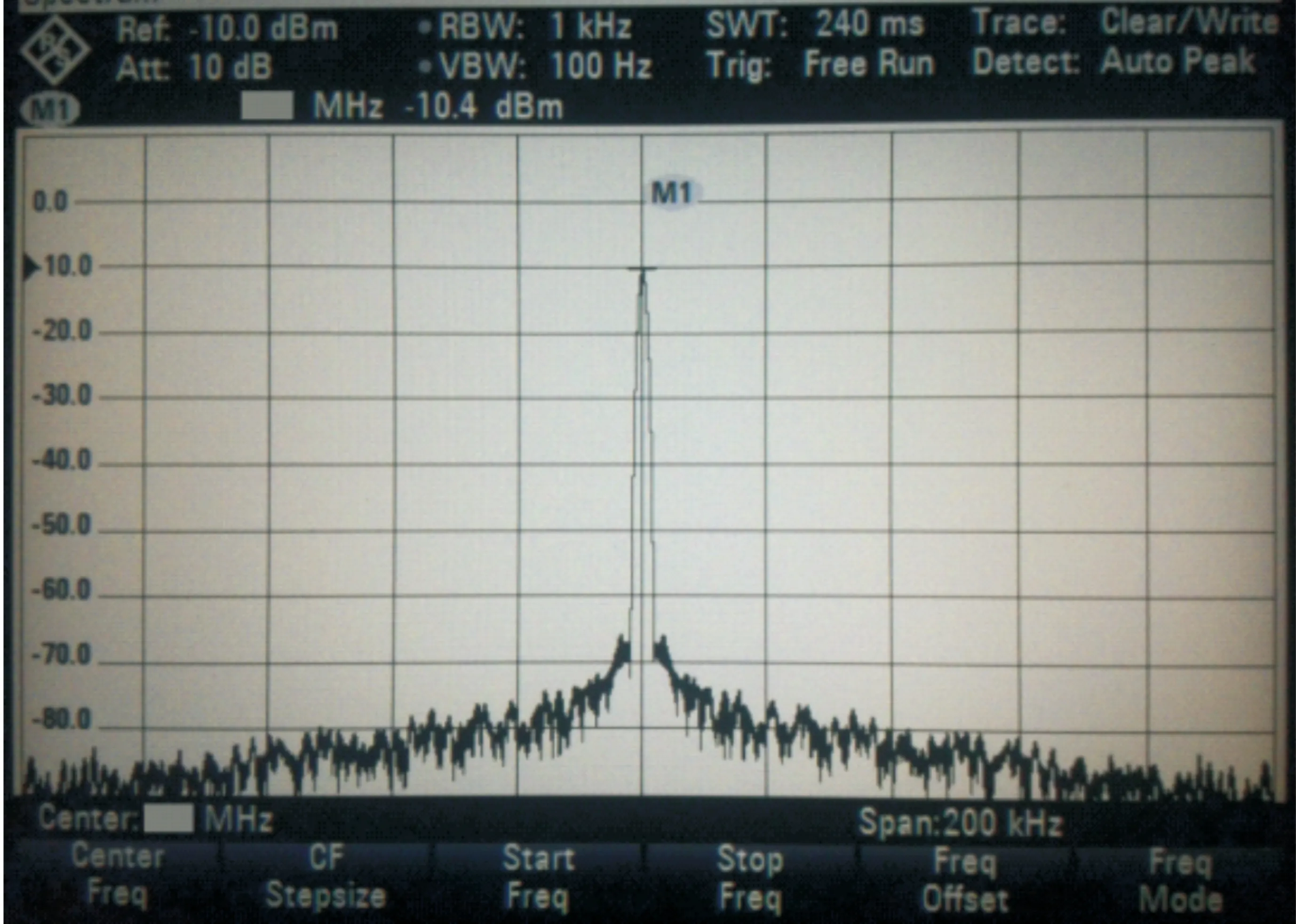

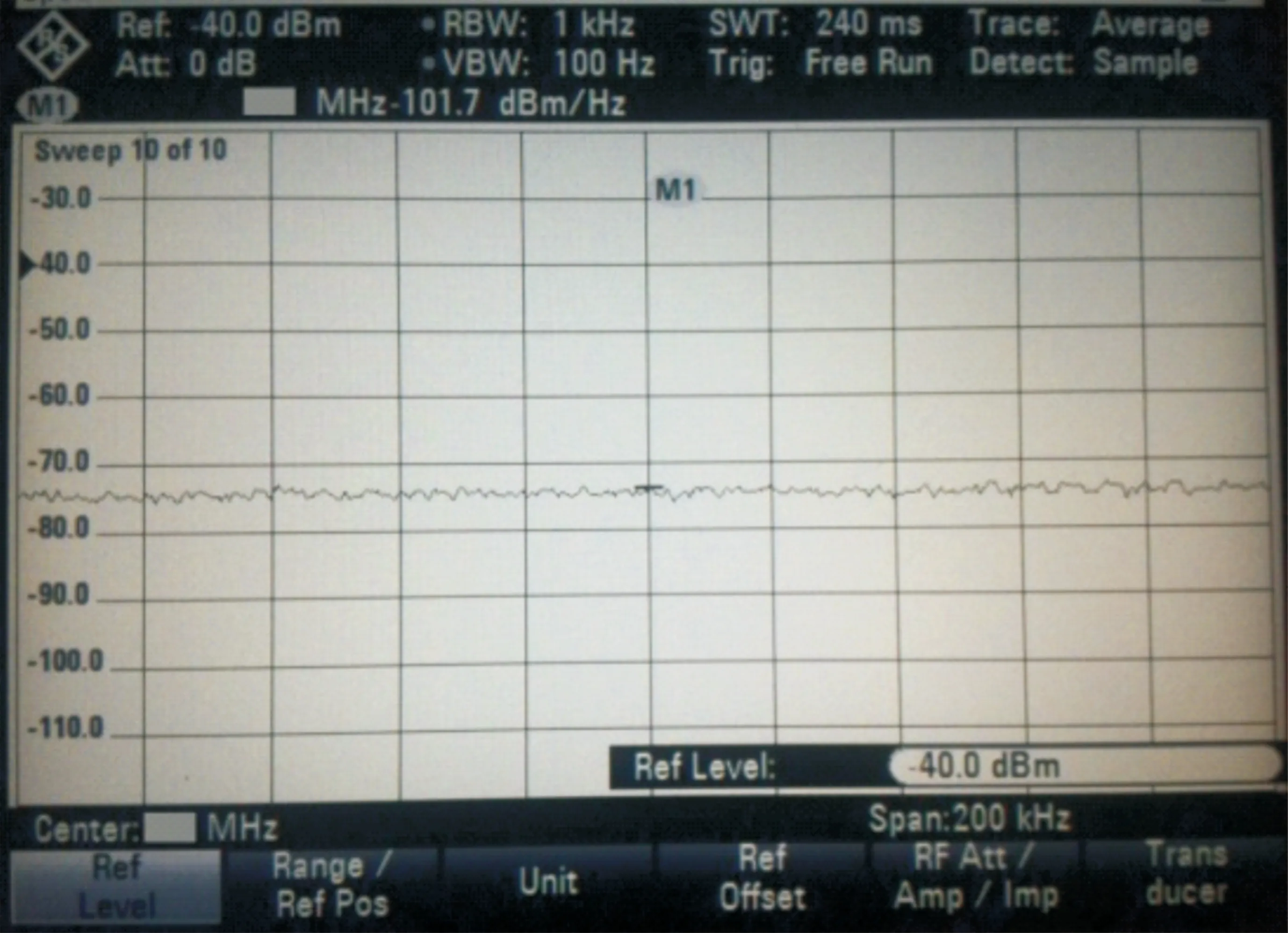

4.2 系统测试
5 结束语

