基于改进的AHP-熵权法的电网综合脆弱性评估方法研究*
2017-12-20丁少倩林涛徐遐龄黄景慧田春筝
丁少倩,林涛,徐遐龄,黄景慧,田春筝
(1.武汉大学 电气工程学院,武汉 430072;2.华中电力调控分中心,武汉 430077;3.国网河南省电力公司经济技术研究院,郑州 450000)
0 引 言
近年来,电力系统大停电事故的频发引起了人们对电网连锁故障传播机理和电力系统脆弱性的关注[1-3],促使各国专家学者从不同角度对大停电事故的原因进行不同层次的分析。全面、科学地辨识和评估系统中潜在薄弱环节是脆弱性概念提出的根本目的,它是目前的研究热点之一。电网脆弱性评估可分为结构脆弱性和状态脆弱性两个重要方面。电网脆弱性不仅与系统状态量有关,又受到电网拓扑特征的影响,只考虑结构脆弱性的评估模型和只考虑状态脆弱性的模型都具有一定的缺陷。如何准确的评估电网的脆弱性及潜在的危险、预防连锁故障的发生,对电网的安全稳定运行具有重要的意义和实际应用价值。
目前电力系统脆弱性的评估方法研究趋势逐渐从单一的结构脆弱性评估向结构脆弱性结合状态脆弱性的综合评估方向靠拢[4-10]。文献[4]提出了基于二维平面拟合的电网脆弱性分析方法,同时考虑电网运行状态量和拓扑参量,但是只从电网运行角度对电网脆弱性做了定性描述;文献[8]引入层次分析法来研究综合脆弱性,只考虑了主观的专家意见,很可能造成决策者主观经验臆断的影响,忽略了客观数据信息。文献[9]提出的综合脆弱性模型虽建立在信息熵和层次分析法理论基础上,但是其中的层次分析法采用三标度法,虽能够保序,但其精度不高。因为标度值越少,对事物的“度量”,就会变得更加粗糙。
文章基于电气介数和电压稳定性理论,综合考虑网架结构的重要性和当前系统运行状态的基础上,提出了基于改进的AHP-熵权法的综合脆弱性评估模型。该方法针对只考虑结构脆弱性的评估模型和只考虑状态脆弱性的模型的不足,运用改进的AHP-熵权法的基本思路来进行综合脆弱性评估;层次分析法采用指数标度法,既有保序性,又能保证判断一致性,评估结果精度较高;熵权法以结构脆弱性和状态脆弱性指标数据为基础赋予相应权重。综合专家的主观意见和客观数据信息,全面整体的描述所评估系统的脆弱特性,科学辨识系统中的潜在薄弱环节。
1 脆弱性评估指标的归一化
文章基于改进的电气介数[7]所得的每条线路的电气介数Be(m,n)作为节点的节点度权重,表示与该节点相连的线路的重要性。由此可得节点i的网架结构重要度,即节点i的结构脆弱性指标:

式中G、L分别表示电网中所有发电机节点和负荷节点的集合;Wi为发电节点i的发电有功功率;Wj为负荷节点j的负荷有功功率;Ii(m,n)发电机节点i单独注入单位电流元ei时在支路(m,n)上引起的电流。
由文献[8]节点i的状态脆弱性指标为:

式中Yi为节点的实际运行电压距离临界值的裕度,Vi为节点i的实际运行电压,Vcr为负荷节点的运行电压临界值。
节点i的结构脆弱性ωsi与状态脆弱性指标ωri量纲不同。因此,建立综合性指标之前,需要先分别对它们进行归一化处理。分别以结构脆弱性指标和状态脆弱性指标的最大值和最小值为基准值,对其脆弱性指标进行归一化处理,得:
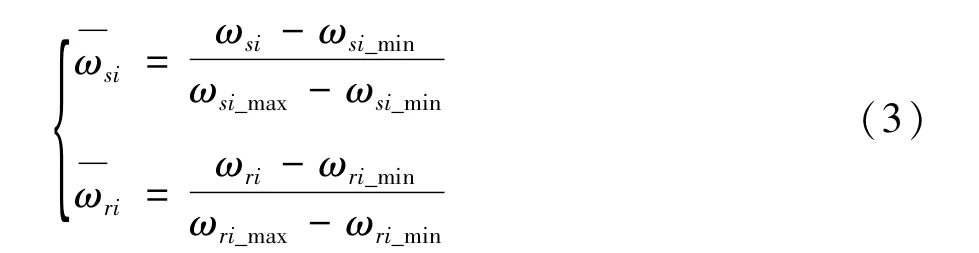
式中ωsi_max、ωsi_min分别为所有节点结构脆弱性指标的最大值和最小值为归一化后节点i的结构脆弱性指标;
ωri_max、ωri_min分别为所有负荷节点状态脆弱性指标的最大值和最小值,ωri为归一化后负荷节点i的状态脆弱性指标,其余节点的状态脆弱性指标为0。
2 综合脆弱性评估模型
在综合脆弱性指标的建立中运用了层次分析法和改进的熵权法相结合基本思路,采用基于改进的AHP-熵权法,采用主客观结合的权重确定方法解决权重系数的权重系数的选取问题。基于层次分析法来实现脆弱性体系层与层之间的权重系数计算,熵权法以数据为基础对层次分析法所得的专家权重进行修正。既可在一定程度上减少主观性带来的干扰,又可避免完全以数据为基础,使评价结果与人们预期的和较认可的结果有较大差异。
2.1 基于层次分析法(AHP法)的专家权重
在层次分析法中,数量化标定子目标相互之间的重要程度的方法即为标度。常用的标度法有1~9标度、9/9~9/1标度、20/2~28/2标度、以及 e0/4~e8/4标度等标度方法[10]。本文考虑到构造判断矩阵的保序性、一致性、标度均匀性、标度权重拟合性等方面因素,故选用 e0/4~e8/4指数标度法构建判断矩阵,如表1所示。层次分析法的基本求解步骤如图1所示。
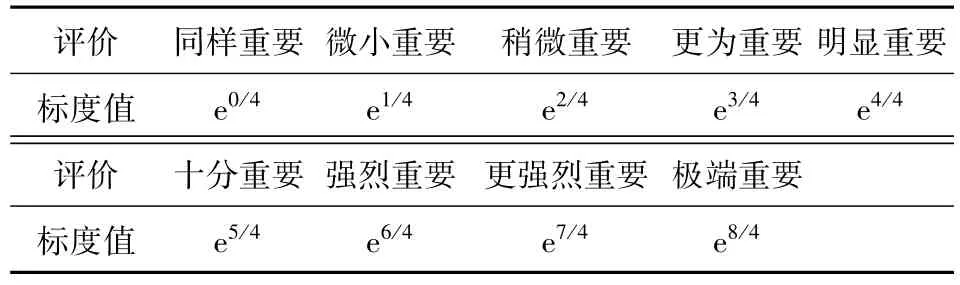
表1 判断矩阵元素含义Tab.1 Exponent scale of judgment matrix
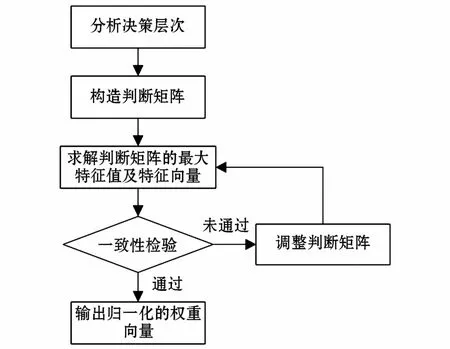
图1 层次分析法的基本思路Fig.1 Flow chart of AHP
本文采用AHP层次分析法对结构脆弱性指标和状态脆弱性指标进行目标融合构造综合目标函数,得到结构脆弱性和状态脆弱性指标专家权重ξ1、ξ2,权重系数取决于结构脆弱性和状态脆弱性在脆弱性评估体系中的重要程度。
2.2 基于改进的熵权法的权重
将电网的全部节点作为评价对象,同时建立两个评价指标:结构脆弱性、状态脆弱性。以期根据客观条件的变化来修正综合脆弱性中其相应权重。改进的熵权法求解的具体步骤如下:
(1)原始矩阵的建立
设电网中有m个节点,即原始矩阵中m个评价对象;有n个评价指标得到的原始矩阵为:

式中xij为第i个评价节点在第j个脆弱性指标上的指标值。
对于某项脆弱性指标j,指标值xij的差异越大,则该指标在综合脆弱性评估中所起的作用越大;若某项脆弱性指标的指标值全部相等,则该指标在综合脆弱性评估中几乎不起作用。
(2)原始矩阵的标准化
电力系统的结构脆弱性,可以科学辨识系统中的关键线路和节点。节点结构脆弱性指标越大,该节点在网架结构中越不稳固,脆弱度越高,属于效益型节点。状态脆弱性从运行状态角度反映抵抗连锁故障或连锁扰动的能力[7]。节点的状态脆弱性越大,说明节点的运行状态越不稳定,脆弱度越高,属于效益型节点。
对原始矩阵做如下标准化处理:
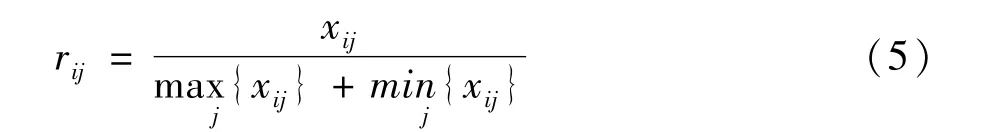
(3)定义熵
在有m个评价节点,n个评价指标的评估问题中,第j个指标的熵定义为:

(4)定义熵权
定义了第j个指标的熵之后,第j个指标的熵权定义为:

相应的指标所占的权重也就越大,说明各节点某项指标上的值相差较大,其传递的有效信息越多;反之,其传递的有效信息越少。
通过纯数值计算方法,以结构脆弱性和状态脆弱性指标为基础,保证了计算过程的客观性。
2.3 综合脆弱性指标的权重系数的确定
电网脆弱性不仅与系统运行状态有关,又受到电网拓扑特征的影响,只考虑结构脆弱性的评估模型和只考虑状态脆弱性的模型都具有一定的缺陷。综合脆弱性指标综合考虑了系统运行状态和电网拓扑特征两个方面的影响,更全面、科学的表征和评估了系统的脆弱性。
本文将熵权法与AHP法相结合,使权重不仅体现出专家的主观意见,还包含客观数据的有效信息,使得到的权重同时反映主观程度和客观程度,即:
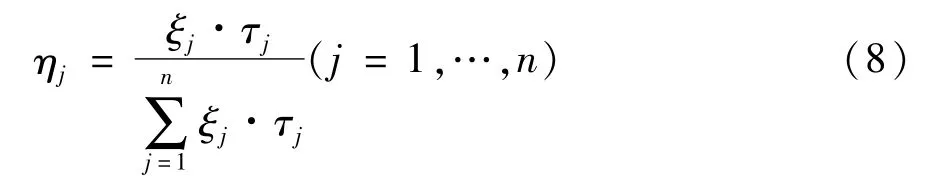
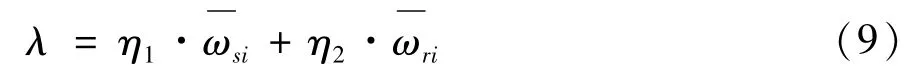
综合脆弱性指标权重可结合具体算例对判断矩阵进行赋值,建立与具体算例和运行方式对应的综合脆弱性指标。
3 实验结果与分析
3.1 基于改进的AHP-熵权法的综合脆弱性分析
选择IEEE-39节点系统作为分析算例,具体参数见文献[11],如图2所示。
式中ξ1、ξ2为结构脆弱性和状态脆弱性指标的专家权重;τ1、τ2为结构脆弱性和状态脆弱性指标相应的熵权值;η1、η2分别为结构脆弱性指标和状态脆弱性指标所占综合权重。
将归一化的结构脆弱性和状态脆弱性分别乘以相应的综合权重,采用加权形式构建目标函数,得到综合脆弱性指标:
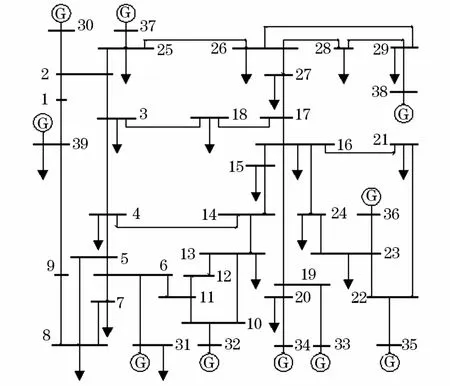
图2 IEEE-39节点系统接线图Fig.2 Wiring diagram of IEEE-39 node power system
采用指数标度法,构建判断矩阵如表2所示。不同算例中的结构脆弱性和状态脆弱性的相对重要性各不一样,需要由指数标度法,根据具体情况对判断矩阵进行赋值并建立与特定算例对应的综合脆弱性指标。
选取算例为大负荷运行方式,表2的构建考虑以下因素:(1)结构脆弱性反映了节点在网架结构中的重要性,但忽略了当前运行方式下的运行状态参数;而状态脆弱性的分析研究大多是基于电网运行越限条件提出裕度指标,而不反映电网的拓扑特征的影响;(2)大负荷运行方式下,系统电压波动较大,故状态脆弱性相对结构脆弱性的重要程度是稍微重要。
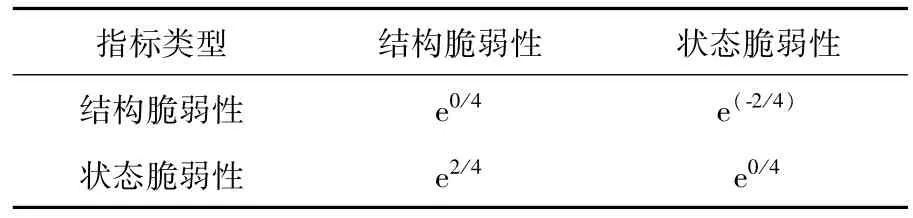
表2 判断矩阵Tab.2 Judgment matrix
由判断矩阵,所得的满足一致性要求的专家权重指标如表3所示。

表3 专家权重Tab.3 Expert weight
由计算所得的节点的结构脆弱性和状态脆弱性指标,得到原始矩阵X。进而得到2种节点脆弱性指标相应的熵和熵权,如表4所示。

表4 节点脆弱性指标的熵和熵权Tab.4 Entropies and entropy weights of the indexes
由表4可知,熵和熵权呈反比关系,熵越小,计算所得的熵权越大,相应的指标所占权重越大。结构脆弱性相对状态脆弱性来说熵权较大,说明39节点算例中各节点在结构脆弱性指标上的值相差较大,该指标提供的有效信息越多。故由表3和表4,可得基于改进的AHP-熵权法的综合脆弱性评估指标,如表5所示。

表5 综合权重Tab.5 Comprehensive weight
分别基于层次分析法、熵权法及改进的AHP-熵权法对算例中进行综合脆弱性的计算,负荷节点的综合脆弱性指标排序结果如表6所示,其综合脆弱性指标结果如图3所示。
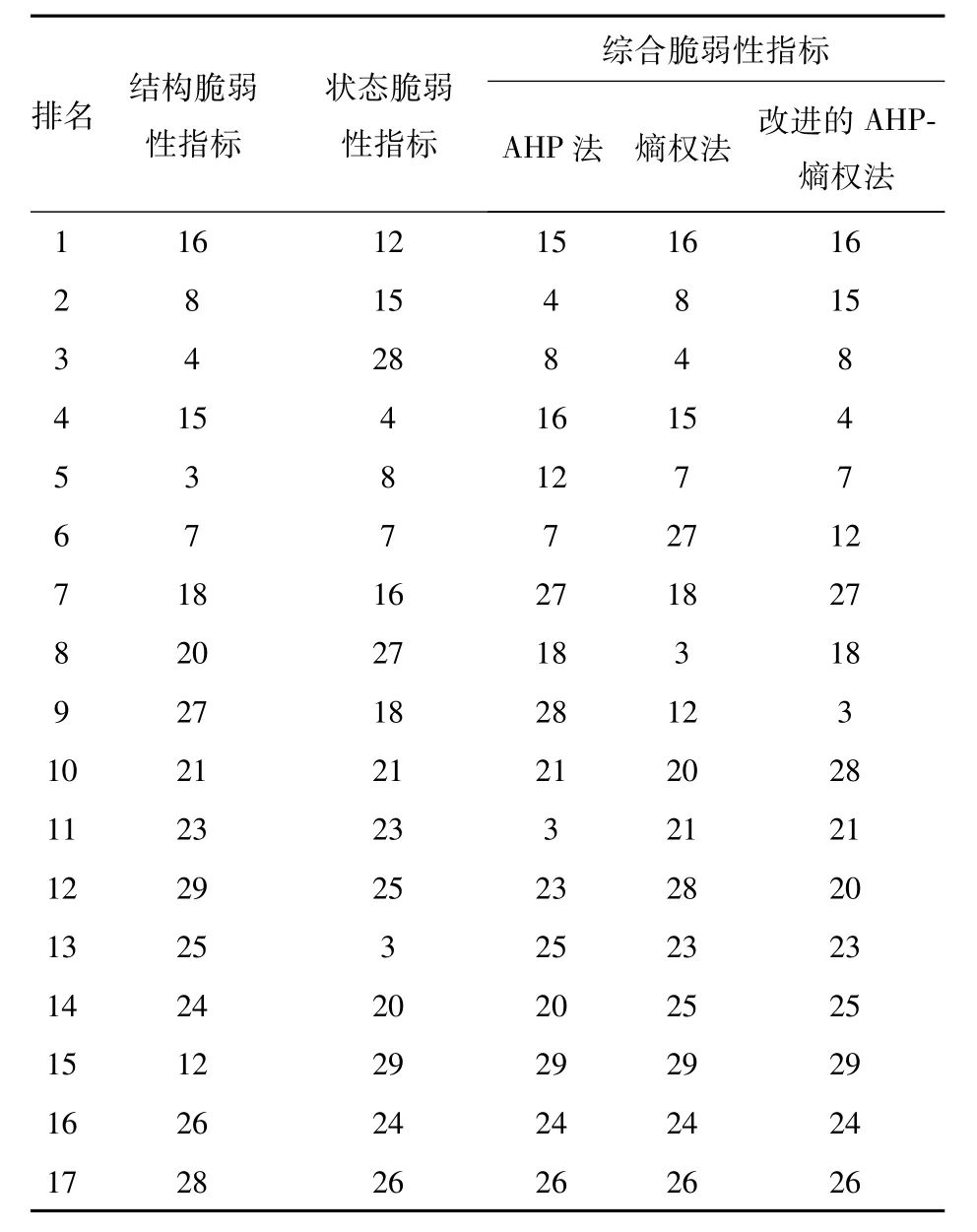
表6 负荷节点综合脆弱性结果排序Tab.6 Results sort of comprehensive vulnerability of load nodes
由表6可以看出,依据改进的AHP-熵权法所得的综合脆弱性指标排序中前3名为节点16、节点15和节点8,节点12排名6位。节点16是全网的重要节点,与网络中其他节点联系紧密,其结构脆弱性指标最高,但其运行状态距离临界状态还有一定裕度,状态脆弱性指标排第7位,基于改进的AHP-熵权法的综合评估后,其综合脆弱性排序为第1位;节点12为处于系统末端的负荷节点,其结构脆弱性值在所有负荷节点中排第15位,但由于运行状态十分脆弱,运行状态比较逼近临界状态,状态脆弱性排序为第1位,因此其综合脆弱性排序上升至第6位,验证了节点在电网中脆弱性由它在网架结构中重要性及运行状态两部分决定这一特性。
依据改进的AHP-熵权法所得综合脆弱性指标排序最末的节点为节点24、26。节点24及节点26所带负荷较小,这些节点故障甚至退出运行对整个网络结构的完整性没有太大影响,故其结构脆弱性很小。且节点24有足够的拥有充足的无功功率支撑,运行状态良好;节点26距离发电机节点37很近,该发电机节点为其提供功率支撑,故其运行状态较稳定,故两者的状态脆弱性指标不大,所以其综合脆弱性最小。因此,本文所述方法可全面地评估节点的综合脆弱性。
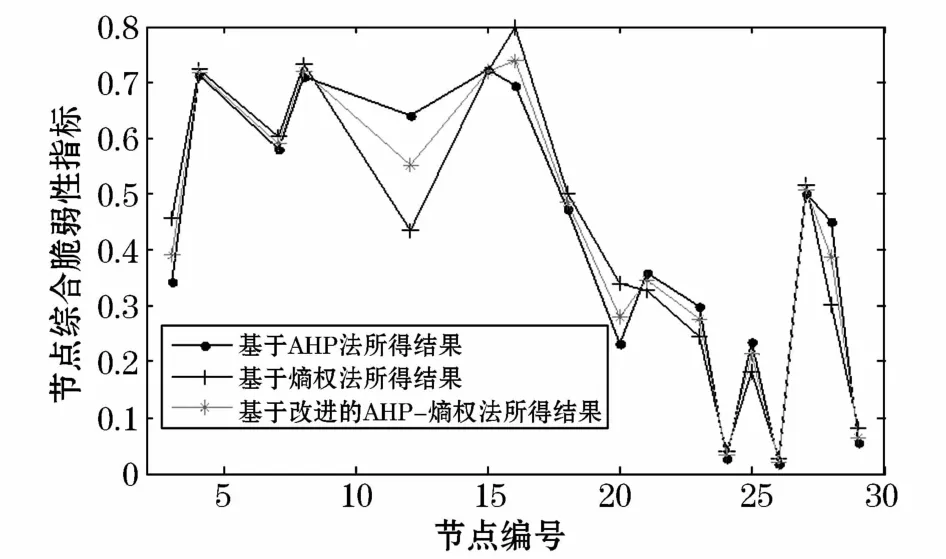
图3 综合脆弱性指标结果对比曲线Fig.3 Results contrast curve of comprehensive vulnerability index
3.2 综合脆弱度指标的验证
由文献[12]可知,针对脆弱性越深的节点进行无功补偿,系统脆弱性的改善程度越大。为了验证本文所述综合脆弱行评估方法的准确性和实用性,假设系统的运行条件不变,利用电力综合程序PSASP软件,分别对节点分别进行相同的无功补偿(5 MVar),比较补偿前后系统综合脆弱指标的变化情况。
分别选取相对而言具有代表性的3个节点:节点16、节点15及节点20,其综合脆弱性指标排序为第1位、第2位及第14位。其综合脆弱性指标变化仿真结果如图4所示。
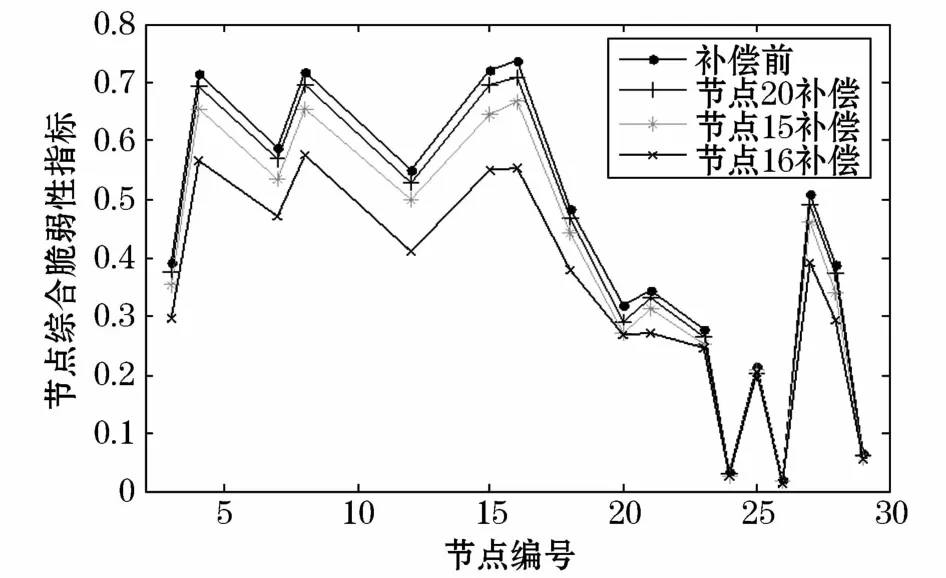
图4 无功补偿前后各节点综合脆弱性指标变化曲线Fig.4 Comprehensive vulnerability index curves in each node before and after compensation
由图4的对比可知,对3个具有代表性的节点进行无功补偿后,综合脆弱性指标曲线呈下降趋势,并且各曲线的间隔不断增大,对不同的节点进行无功补偿,其影响程度不同。其中对节点16进行无功补偿后对系统其它节点的综合脆弱性改善效果最佳,节点15次之,节点20效果最弱。这说明节点20运行较为稳定、节点15次之,节点16脆弱程度最深。与本文所述综合脆弱性指标排序相符,证明了本文所述方法的准确性。
从而也表明AHP法通过专家们对指标进行两两比较,主观地对比分析指标的相对重要性程度得出综合脆弱性评估结果,结论难免偏颇;熵权法以数据为基础,给出的综合脆弱性评估结论相对客观;AHP-熵权法确定的综合权重则综合了节点专家意见和客观数据信息,两者互补,更全面评价系统的脆弱特性,科学辨识薄弱节点。部分节点的具体仿果如表7所示。
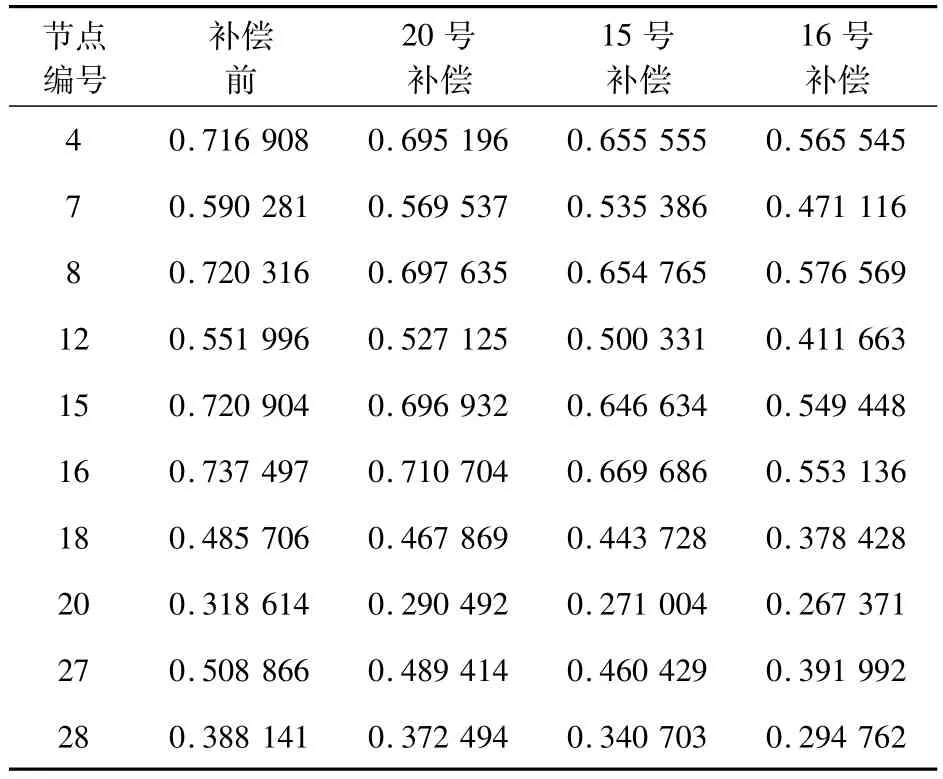
表7 负荷节点综合脆弱性结果排序Tab.7 Result sort of integrative vulnerability of load nodes
4 结束语
提出了基于改进的AHP-熵权法的综合脆弱性评估模型。结合网架拓扑结构和当前系统运行状态参数,将改进的AHP-熵权法运用到脆弱性理论的研究之中,综合节点的专家的主观意见和客观数据信息,可全面整体的描述所评估系统的脆弱特性,科学辨识系统中的薄弱节点。通过IEEE 39节点系统验证评估方法的合理性与有效性。
所述评估方法物理概念清晰,计算方法简单,有在线应用的前景,综合评估系统抵御连锁故障或连锁扰动的能力,可为电力系统的安全防御提供合理有效的决策依据,值得进一步研究。
