基于电气阻尼计算的STATCOM次同步振荡控制器设计*

谢珍建，蔡晖，黄俊辉，季杭为，祁万春，赵欣

（1.国网江苏省电力公司经济技术研究院，南京210008；2.东南大学 电气工程学院，南京210096）

0 引 言

次同步振荡（Sub Synchronous Oscillation，SSO）属于电力系统的一种不稳定运行状态，长期处于这种状态会导致大型汽轮发电机转子轴系的严重破坏，甚至断裂，从而危害电力系统的安全稳定运行［1］，一般是发生在串补电力系统中。HVDC、PSS和FACTS等，由于对次同步频率范围内的功率和速度变化响应灵敏，也有可能激发 SSO问题［2］。但FACTS装置的灵活快速调节能力，亦可用于抑制次同步振荡，如 SVC、TCSC和 STATCOM等［3-5］。

静止同步补偿器（STATCOM）是一种有源FACTS元件，它的运行范围宽，调节速度更快，亦可附加控制来抑制次同步振荡。文献［6］首次利用STATCOM来抑制次同步振荡，将STATCOM置于发电机出口侧，观察系统特征值的变化来确定附加阻尼控制器的参数。文献［7］则将STATCOM安装在升压变高压侧，同样运用特征值分析法来确定控制参数。文献［8-9］则将STATCOM并联在IEEE第二标准测试系统的无穷大电源前，分别探讨了以计算出的内部电压（Computed Internal Voltage，CIV）和内部相角（Computed Internal Angle，CIA）为附加控制输入时对SSO的抑制效果，但没有提及控制参数的整定方法。文献［10-11］将STATCOM并联于线路中点，采用计算得到的戴维南电压和从滤波器得到的次同步电流为控制信号，提出了一种基于电气阻尼的参数设计方法，但没有简化阻尼的计算过程。文献［12］提出了通过发电机转速偏差对STATCOM输出电压进行调制来抑制SSO的策略。文献［13］则在计算扭振模态互补频率电流补偿相位的基础上，给出了控制器参数。但以上两种基于阻尼的设计方法，对如何选取各扭振频下的补偿相位仍缺乏标准。文献［14］提出扰动后STATCOM可以工作在相间不平衡模式（phase imbalanced mode）一段时间来抑制SSO。文献［15］提出了网侧 STATCOM为主、机侧SEDC为辅的联合抑制措施。

总体来说，STATCOM抑制次同步振荡的研究受到了广泛关注。传统的特征值分析法在设计时的计算量较大，基于电气阻尼的方法虽然在速度上有优势，但仍有改进的空间，同时在各扭振频待补偿相位的确定还需建立一定的规则。文中首先简化了复转矩系数和电气阻尼的计算，推导出含STATCOM系统的电气阻尼表达式。然后基于该阻尼表达式分析了STATCOM控制下的系统特性变化。最后确定了控制器相位补偿的优化目标，并利用遗传算法来求解，以抑制电力系统次同步振荡。

1 含STATCOM系统的电气阻尼推导

复转矩系数法对于次同步振荡的判断，是分别求出机械转矩和电磁转矩对转子角位移振荡的响应，得到机械复转矩系数和电气复转矩系数。在此基础上，分析复转矩系数中的弹性系数和阻尼系数（简称阻尼），认为如果在发电机的某个自然扭振频率附近，总弹性系数等于零时总阻尼小于零，该系统就会发生次同步振荡。由于机械阻尼只和发电机机械部分有关，不随系统运行状态变化而改变，所以阻尼的计算主要受到电气部分的影响［16］。为推导电气阻尼表达式，采用如图1的IEEE第一标准测试系统，可在其输电线路中点并联一STATCOM。

1.1 STATCOM的数学模型

如图1所示，STATCOM大都采用电压型桥式电路，将直流电压逆变为交流电压后通过变压器接入系统。忽略变流器损耗，可得到dq轴下交流侧和直流侧的微分方程为：

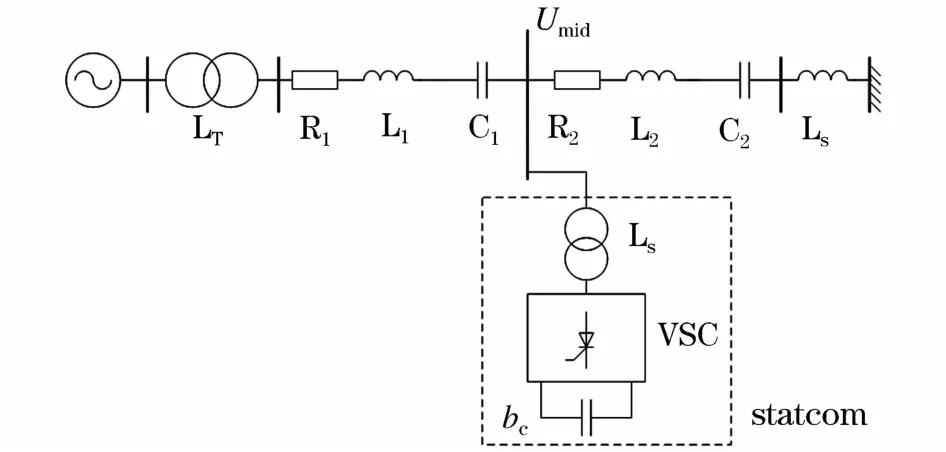
图1 含STATCOM的IEEE第一标准测试系统Fig.1 The first IEEE standard test system with STATCOM

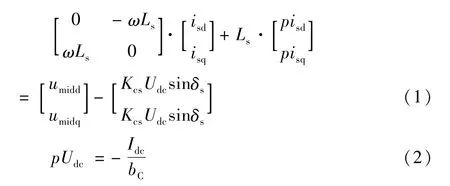
式中Kcs是连接交流与直流电压的常数，常见的12脉波VSC中代表STATCOM交流侧输出电压与q轴的夹角，而接入点电压δmid＝δs-θd。考虑到变流器交流端和直流端的瞬时功率相等，有：

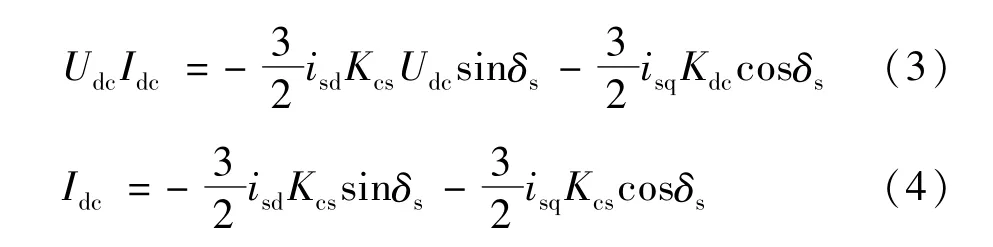
将式（3）和式（4）代入式（1）和式（2）并线性化，即可得到以isd、isq和Udc为状态变量的STATCOM电磁暂态模型。

1.2 系统电气阻尼推导

根据文献［3］，Y＝1／z在 dq轴上的形式为Ydq且电路串联和并联阻抗的计算方法仍相同，p＝jξ时：

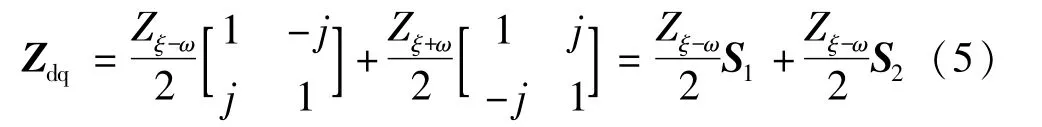
式中zξ-ω和zξ+ω分别表示频率ξ-ω和ξ+ω下的阻抗值。定义STATCOM线路部分在dq轴的阻抗为zs，dq，线性化 STATCOM的数学模型有：

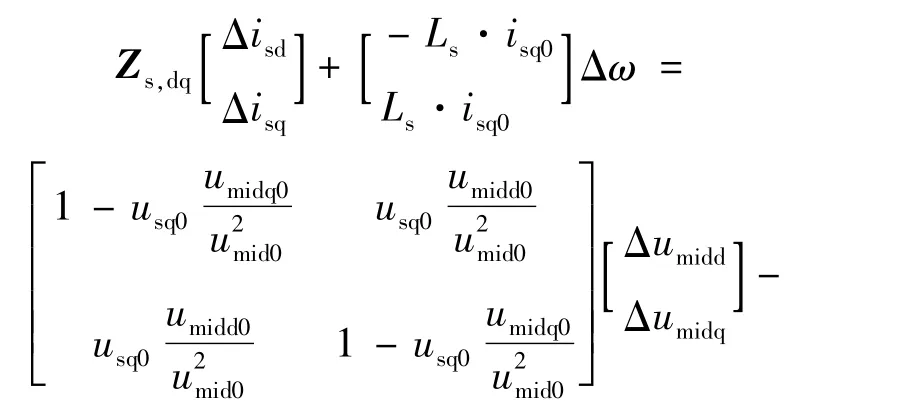
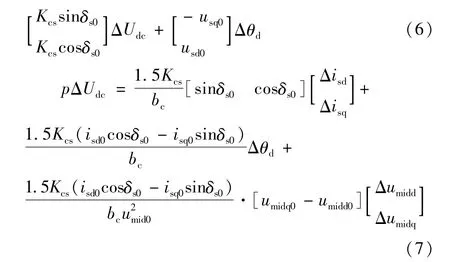
假设STATCOM采用图2的电压调节。

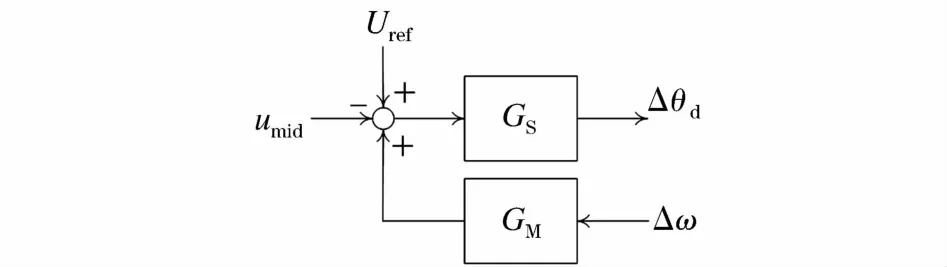
图2 STATCOM控制框图Fig.2 Control block diagram of STATCOM

并考虑以发电机转速为控制信号附加阻尼控制，其线性化的控制模型为：

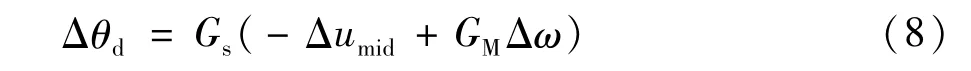
将式（7）和式（8）代入式（6），合并后可得：

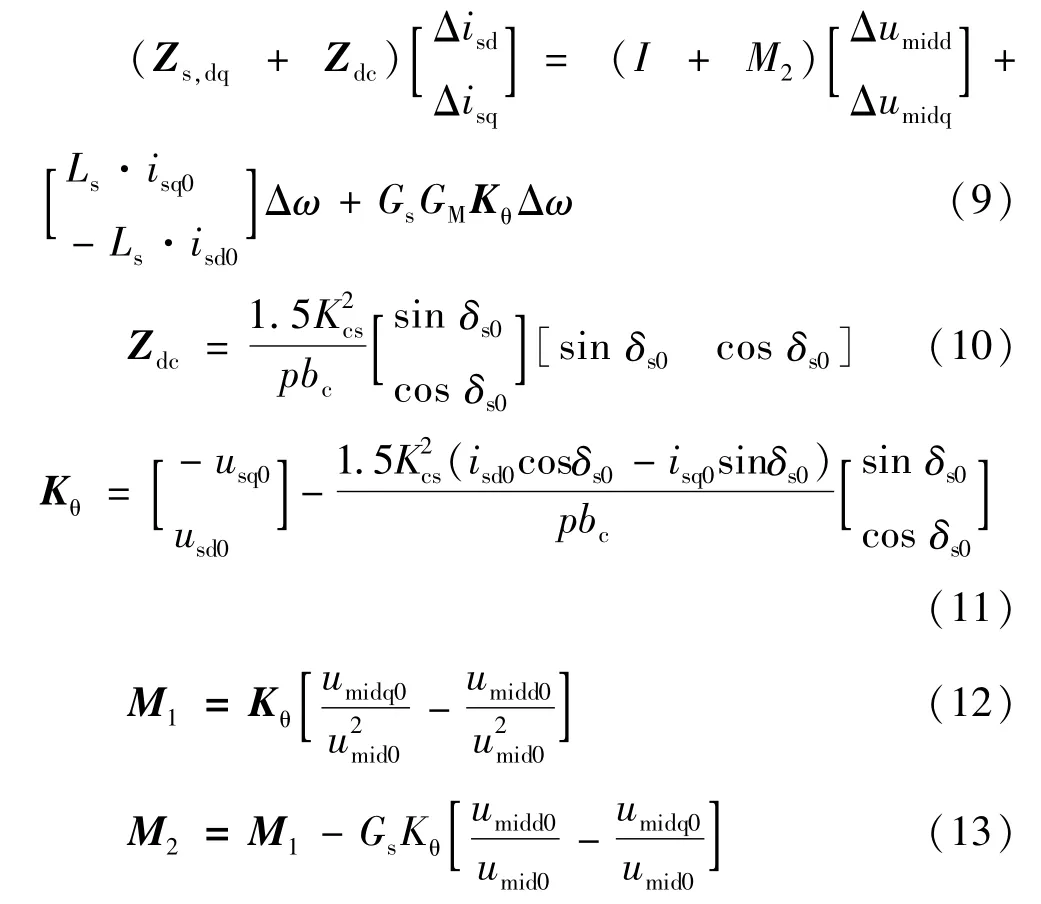
再设定后半段线路、前半段线路、电机内部电路和STATCOM直流侧的阻抗在dq轴上分别为Z2，dq、ZL1，dq、ZG，dq、Zdc，则：

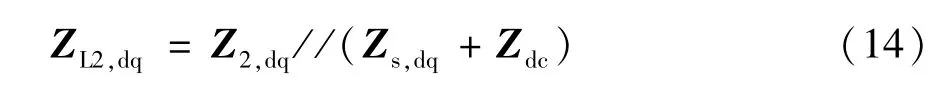
同时将后半段线路的线性化式改写为：

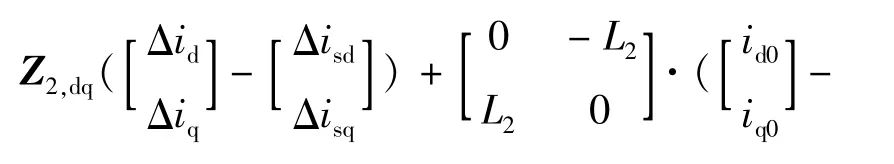
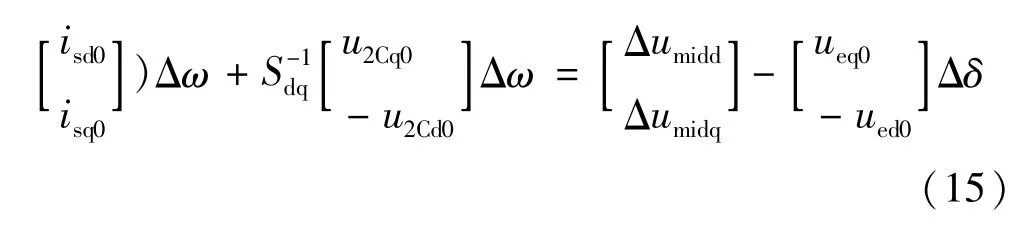
将式（14）代入式（15），稳态值一般可以近似用Umiddq0＝［umidd0umidq0］T和idq0＝［id0iq0］T替换，有：

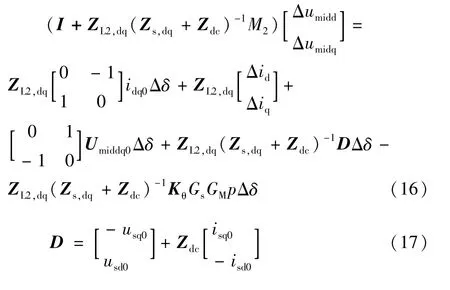
前半段线路的线性化式如下：

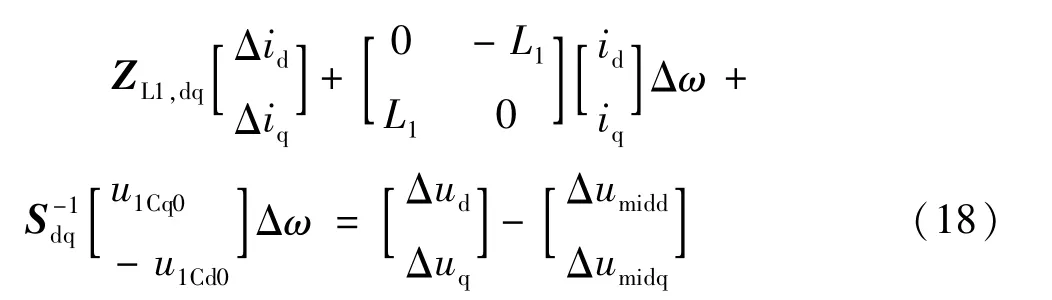
将式（16）代入式（18），整理后得到：

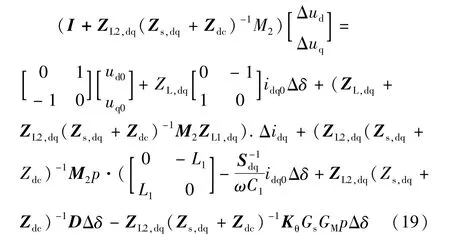
计及发电机内部电路的影响［3］，并令 ZGL，dq＝ZG，dq+ZL，dq，可得到：

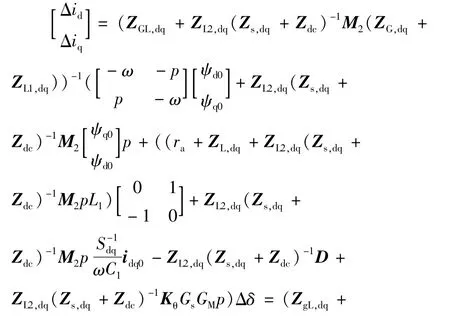
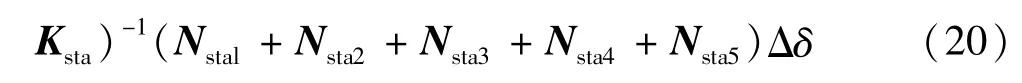
近似求出含STATCOM系统的电气阻尼为：

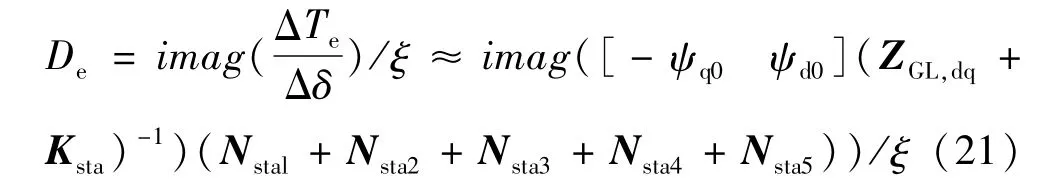
2 STATCOM次同步振荡控制器的设计

实际系统中发电机机械部分的详细参数是很难获取的，大量研究表明机械阻尼在多数情况下绝对值很小，可以忽略［17-18］。从而可认为当电气阻尼在某个固有扭振频附近为较大负值时，次同步振荡就很有可能发生。所以抑制SSO的关键在于使电气阻尼变为正值。那么对于设计STATCOM次同步振荡控制器来说，就是要通过STATCOM的附加控制部分来附加正的电气阻尼，以提高系统整体阻尼情况。

2.1 电气阻尼分析

分析电气阻尼计算式（21）可知，阻尼主要和输电线路阻抗即zGL，dq有关。同时由于STATCOM控制了自身交流出口侧电压Us和接入点电压Umid之间的相位角θd，且自带电压控制，阻尼也受到Ksta电压控制的影响。但电压控制主要和电磁量相关，包含的次同步扭振信息很小，对系统次同步频率下的阻尼特性影响不大。

先不考虑附加阻尼控制，仅有电压控制Δθd＝-GsΔumid时：

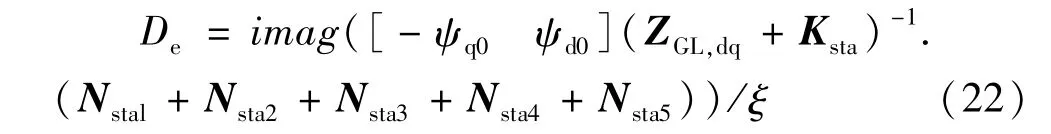
在此基础上附加阻尼控制，其增加的阻尼为：

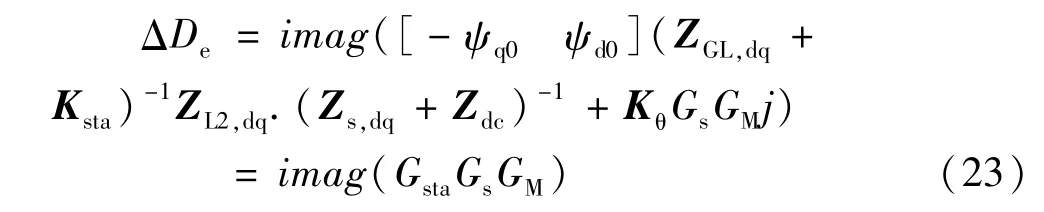
从上式可以看出，电压控制会通过Gs来影响附加阻尼的幅相特性。同时，zdc和Kθ也会改变附加阻尼控制的相位等。

2.2 STATCOM抑制次同步振荡的设计

根据之前的分析，利用STATCOM来抑制SSO，就是要使式（23）所示的附加电气阻尼ΔDe在发电机各固有扭振频均为较大正值，以使总电气阻尼为正。这首先要使附加阻尼为正，即要求各扭振频下的angle（ΔDe）均在0°～180°之间。如果在某个扭振频下angle（ΔDe）为 90°，幅值不变的情况下 ΔDe将最大，阻尼效果最好。但一般发电机均具有多个扭振频率，附加控制无法在每个扭振频均补偿90°。故有必要对所有扭振频的补偿相位进行优化，使其均能接近90°这个最优值。

考虑如图3所示的STATCOM的附加阻尼控制器框图。

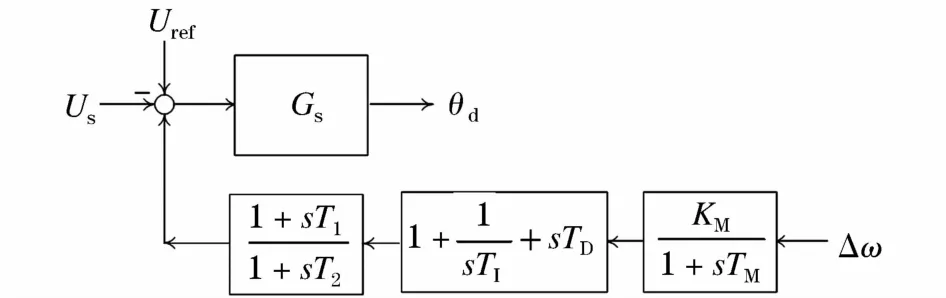
图3 STATCOM附加阻尼控制调节框图Fig.3 The additional damping control block diagram of STATCOM

在惯有的比例采样环节后，采用PID控制［18-19］和相位补偿环节相串联的结构，以扩大相位调节的范围。那么附加阻尼控制器的相位优化设计问题目标函数可写成：

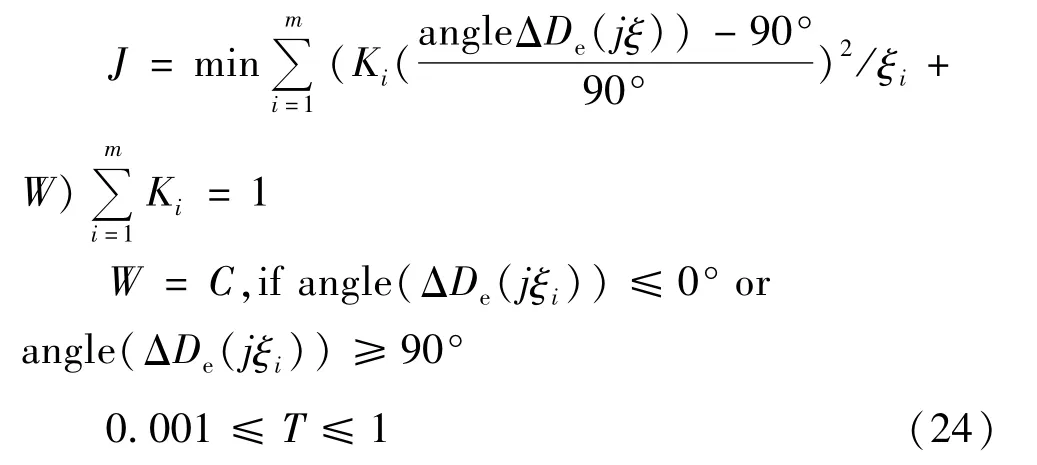
目标函数整体上是使所有扭振频处的angle（ΔDe）与90°差的平方和最小。式中ξi代表第i个扭振频的频率，平方和再除以ξi，是因为扭振频率不同会影响相关模态分量的衰减时间。Ki为第i个扭振频的权重，所有扭振频下的权重之和为1，从而使相位补偿能够更好地顾及已经失稳或接近失稳的扭振频。W为惩罚因子，而C为一较大正常数，用于避免扭振频下的补偿相位超出限值。待优化的变量为T＝［T1T2TITDTM］，取值范围为（0.001，1）。

对于以上的非线性优化问题，可以采用遗传算法进行优化。遗传算法（Genetic Algorithm，简称GA）是以遗传理论和自然选择为基础的高效全局寻优搜索算法。它的基本思想是对自然界生物进化过程的模拟，通过人工进化的方式随机优化搜索目标空间。在算法的实现过程中，用群体的一个个体或染色体描述优化问题中的可能解，每个染色体用与其结构相似的符号串形式表示，反复对个体组成的群体进行遗传学的操作，以适应度函数作为评价个体好坏的准则，从而准确模拟生物的自然淘汰和遗传选择的进化过程。

在用遗传算法求得附加阻尼控制器中的各时间常数后，就已经保证了各扭振频下的附加阻尼为正，通过不断放大KM就可以不断提高阻尼的大小。

3 算例验证

改造IEEE第一标准测试系统，在其线路中点并联一 STATCOM（R1＝R2＝R／2，XL1＝XL2＝XL／2，C1＝0，C2＝C），并且采用如图2所示的控制框图。假设STATCOM的电压控制Gs为比例采样环节Ks＝0.1，Ts＝0.002 s，可以得到STATCOM开环控制和仅有电压控制时的次同步电气阻尼特性如图4所示。从中可以看出，电压控制对阻尼的影响很小，如之前的分析一样，是因为STATCOM的电压控制中包含的机械部分信息很少。表1中的特征值和图5中的转速仿真进一步验证了这一观点。

图4 含STATCOM系统次同步频率下的电气阻尼Fig.4 System electrical damping of sub-synchronous frequency with STATCOM

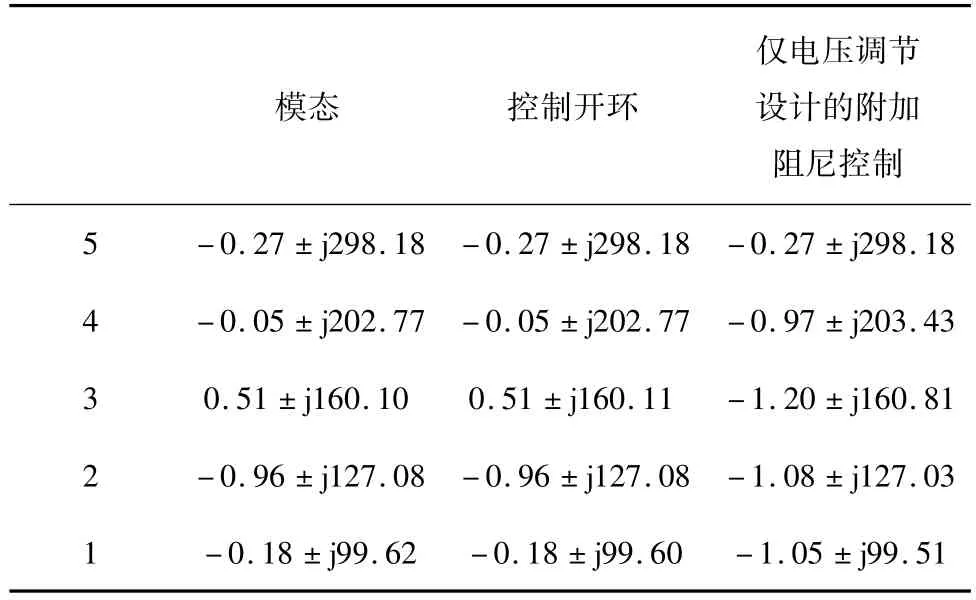
表1 含STATCOM系统的特征值Tab.1 Eigenvalues of the system with STATCOM

电气阻尼曲线显示系统在固有扭振频25.5 Hz处的电气阻尼为负，会发生次同步振荡。扭振频率32.3 Hz处的电气阻尼也为负值，存在一定的风险。为抑制次同步振荡，建立如式（24）所示的目标函数。其中K2＝K3＝K4＝0.3，b1＝b5＝0.05，以较多地考虑可能发生不稳定的三个模态2、3、4。同时，设定惩罚项为10，避免相位补偿角度超出正阻尼范围的情况发生。

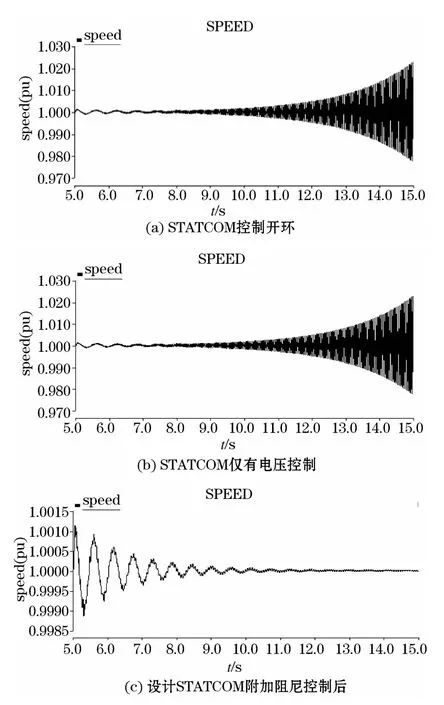
图5 含STATCOM系统的转速Fig.5 Rotational speed of the system with STATCOM

为了遗传算法能更快地收敛，预先给出一组较好的初始解。根据表2中的相位特性，先设定TM＝0.002 s。尽量兼顾可能失稳的扭振频率，接着设定相位补偿环节在扭振频率25.6 Hz处补偿70°，以及PID环节在32.3 Hz补偿50°，在15.7 Hz补偿5°，可得到T1＝0.035 s，T2＝0.001 s，TI＝0.015 s，TD＝0.007 s。从而得到一组可行解［0.035 0.001 0.015 0.007 0.002］。

采用遗传算法求解这一优化问题，设定群体大小为50，终止进化代数为200，交叉概率为0.5，变异概率为0.005。当进化个体满足要求或进化超过代数，停止计算，否则继续，可得到优化解为［0.049 0.001 0.003 0.014 0.001］。在此解基础上，逐步放大KM，用简化阻尼算式（21）计算附加控制后的系统总阻尼，保证在每个固有扭振频下的附加阻尼均为一大于零的正值，最终选定KM＝4。

表2 含STATCOM系统的相位Tab.2 Phase of the system with STATCOM

附加设计的阻尼控制后，电气阻尼曲线如图4所示。明显可看出，在整个次同步频段，电气阻尼均大于零，满足复转矩系数系统不发生次同步振荡的判据。表2中也显示各模态特征值实部都是负值，且除了机械部分阻尼较大的模态5之外4个模态的特征值值实部大致相当，说明权重的设置是有效的。含STATCOM系统的转速如图5所示。图5（c）给出了含STATCOM系统附加阻尼控制后的仿真，验证了所设计的控制器可以很好地抑制次同步振荡。

4 结束语

提出了一种基于电气阻尼计算的STATCOM附加阻尼控制器的设计方法。首先，简化推导了含STATCOM系统电气阻尼表达式。进一步对该算式的分析表明，含STATCOM系统阻尼仍主要和输电线路阻抗有关。虽然其本身的电压控制等对各扭振频的电气阻尼影响不大，但会给附加阻尼控制的相位设计带来困难。故本文将控制器的相位参数设计转化成一个优化问题，计及各扭振频率的影响，并用遗传算法求解。特征值与电磁暂态时域仿真均表明该控制器能有效抑制系统的次同步振荡。