基于改进UPF滤波算法的稳态及短路电流下光学电流互感器信噪分离研究*

欧阳进，张蓝宇，黄阳岗，严宇恒，李岩松

（1.国网湖南省电力公司长沙供电分公司，长沙410000；2.国网浙江省电力公司宁波鄞州区供电分公司，浙江宁波315000；3.华北电力大学电气与电子工程学院，北京102206）

0 引 言

随着数字化变电站的推广，传统的电磁式互感器已难以满足以上提到的种种要求。基于Faraday磁光效应的光学电流互感器（Optical Current Transducer，OCT）具有优良的绝缘性能和良好的动态响应能力，相比与传统的电磁式电流互感器，它的优点有：消除了磁饱和现象、优良的绝缘性能、消除了铁磁谐振抗电磁干扰强、动态响应能力与电流大小无关、适应于数字化变电站的要求等。但是目前在光学电流互感器的实用化道路上依然存在一些问题［1-2］。

磁光玻璃型OCT采用逆磁性材料制成的传感头，能够有效减小非线性误差以及各谐波引起的畸变，然而当测量电流很小时，测量得到的内部噪声信号往往大于光电信号，同时干扰信号与被测信号具有频段相重叠的特点，故障时还可能出现“强噪声，弱信号”现象［3］，导致输出信噪比低、测量精度低、难于还原的问题，这使得很难从频域的角度，用传统的滤波器来消除噪声的影响［4］。而粒子滤波能够有效的克服传统方法的不足，解决电力系统交流量的非线性变化问题，适用于非线性非高斯的随机系统［5］，在数字信号处理中采用FPGA能够实现高速信号处理，保证滤波算法的实时性［6］。但粒子滤波在低信噪比状况下，信噪分离下降。因此如何解决这个问题对进一步推广在时域角度上进行滤波的粒子滤波有着重要意义。

粒子滤波的精度取决状态方程和预测方程的准确性，但是电力系统发生三相短路时，OCT采集的短路电流显然不同于稳态电流，也就是粒子滤波的状态方程不同，这将导致滤波结果存在很大误差。目前对这方面的研究还很空白，制约着粒子滤波的发展。

为了解决上述问题，本文提出基于一种基于全局采样的改进无迹粒子滤波（unscented particle filtering，UPF）的方法，针对低信噪比状况，提高了OCT的滤波精度和信噪分离的能力，同时提高计算速度保证滤波的实时性。在基于全局采样的改进无迹粒子滤波基础上，本文提出了基于阈值的方法解决三相短路时OCT的滤波问题，能够及时、准确地滤波，保证继电保护设备能可靠灵敏动作，确保电力系统的安全运行。

1 光学电流互感器信噪特性

光学电流互感器的基本依据是法拉第效应［7-8］，当光传播的路线围绕载流导体绕N圈的闭合环路时，由安培环路定律可知：

因此要测量输入电流i，只需要测量出法拉第旋转角θ。但是目前尚无高精确度测量法拉第旋转角θ的检测器，因此根据马吕斯定律，通常用检偏器将线偏振光的偏转角信号转换为光强信号，再将光强信号转换为可测的电信号提供给二次侧进行信号处理，在这个过程中产生了内部噪声［9］。

对光学电流互感器实际投运情况分析发现，OCT中对测量准确度影响较大的噪声频率主要处于数十到数百Hz范围内［10］，电力系统50 Hz的工频交流电流与直流电流也处在噪声频率的范围内。在测量小电流时，有用电压信号叠加在基本光强上，其幅值非常小，需由放大器把信号幅度放大，但同时也把噪声放大，导致信号往往小于信号噪声，降低了输出信噪比。因此必须采用别的方法消除噪声影响。UPF算法在进行非线性滤波同时，结合了最近的量测值，使得该方法适用于上述提到的情况。

2 基于全局采样的UPF改进算法

粒子滤波（PF）本质上是一种基于贝叶斯学习框架下的序贯蒙特卡洛方法，在处理非高斯、非线性时变系统的参数估计问题和状态滤波具有广阔的应用前景［11］。

标准粒子滤波由序贯重要性采样（SIS）和重采样构成，鲁棒性较好，能较好的解决强非线性非高斯问题［12］。在标准粒子滤波中，算法的准确度极大程度上依赖于建议分布的选择，当选择的重要性密度函数（即建议分布）与真实情况存在较大的偏差时，将会导致滤波算法的滤波结果偏差较大，甚至导致滤波发散。

UPF算法能够很好地解决这个问题，其在每个新的观测值采集之后，先通过无迹卡尔曼滤波（UKF）产生最优的高斯分布来替代重要性分布，这个建议分布将实时观测信息融入到了重要性密度函数中，使更多地粒子分布在似然函数值较高的区域，极大提高了滤波精度［13-14］。

但是UPF存在着计算量大的缺点［15］，即在得到建议分布时，每一个粒子都需要进行一次UKF算法，这就相当于每次迭代中，都需要预测更新N个粒子的均值和方差，每一个粒子的建议分布都由对应的高斯分布N产生，随着采样粒子数的增加计算量急剧增大，降低了该方法应用在OCT滤波时的实时性。

为了提高该方法的实时性，本文提出了基于全局采样的改进UPF方法，并将其应用到OCT的信噪分离当中。通过对k－1时刻的N个采样粒子求取粒子集，得到粒子集的均值和方差 Pk，利用最新的观测值zk＋1对粒子集进行UKF更新，得到k＋1时刻粒子集的状态均值和方差 Pk＋1，这就是符合高斯分布的建议分布。对这个建议分布进行N次采样得到最新时刻的N个粒子点集。

改进后的UPF算法通过粒子集代替N个粒子进行UKF算法更新；再对粒子集进行N次采用，避免了粒子的退化现象，因此改进后的UPF算法不再重采样。改进算法从这两个方面节约了大量的计算时间。

基于全局采样的改进UPF的OCT滤波算法具体步骤如下：

第一步，初始化。对先验参考分布p（x0）进行采样得到 N个粒子，即，令权值＝1／N，i＝1，…，N。

第二步，计算粒子集均值和方差。

第三步，利用UKF预测及更新k时刻粒子集的均值和方差。

（1）计算2n＋1个sigma点（即采样点，n是状态向量维数）。

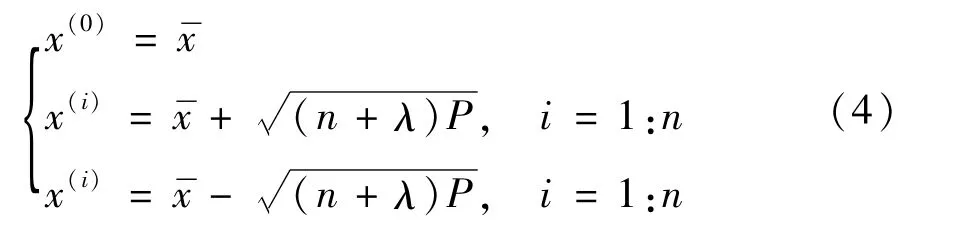
（2）计算这些采样点相应的权重。

式中 λ＝α2（n＋k）－n，k为比例参数，通常情况下应确保后验协方差的半正定性，对高斯分布的情况，当状态变量为单变量时，选择，当状态变量为多维时，一般选择k＝0。

（3）将采样点代入状态方程，得到状态一步预测：

（4）系统状态一步预测及协方差矩阵为：

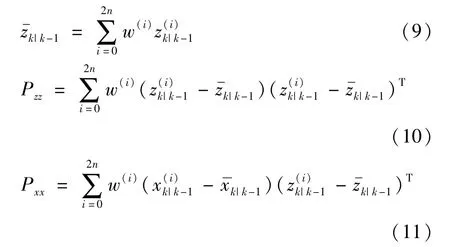
通过状态和方差更新，计算滤波增益：

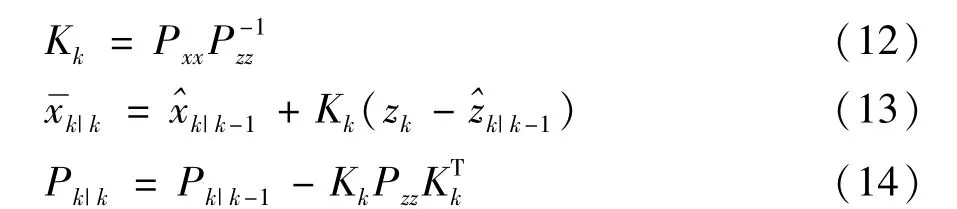
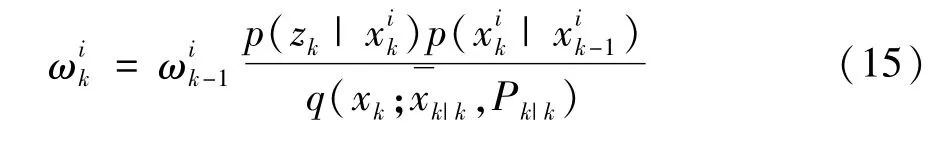
（4）状态更新

第五步，循环计算，另k＝k＋1，如结束则退出，否则跳转到第二步。

3 稳态时改进UPF方法信噪分离仿真验证

在电力系统中，OCT的输入信号为交流分量、直流分量和随机噪声的叠加，在只考虑基波的情况下，系统的状态方程和量测方程如式（17）表示：

式中y为OCT的量测值；x1表示交流量的幅值；x2表示交流量的初相；x3表示OCT中的直流量；vk－1为直流量和交流量的过程噪声；nkN（0，）为OCT中的随机噪声。

电力系统中的频率一般在50 Hz左右，所以当频率等于50 Hz时，t时刻OCT的量测值的为：

为了模拟OCT的低信噪比特性，设x1，x2，x3初值为0.2、0、5，OCT的量测值为 y（t）＝0.2sin（50πt＋0）＋5，高斯白噪声幅值为0.5，为输入交流分量的2.5倍，信噪比为－4 dB，含噪声的输入信号波形如图1所示。相关参数设置如下：粒子数N＝100，采样率为10 kHz，即算法每0.000 1 s递推一次。

图1 加噪后的电流波形Fig.1 Current waveform plus noise

首先，在低信噪比状况下，分别采用改进的UPF算法与粒子滤波对含噪声的测量电流进行信噪分离，分离得到的交流分量和直流分量结果分别如图2、图3所示。

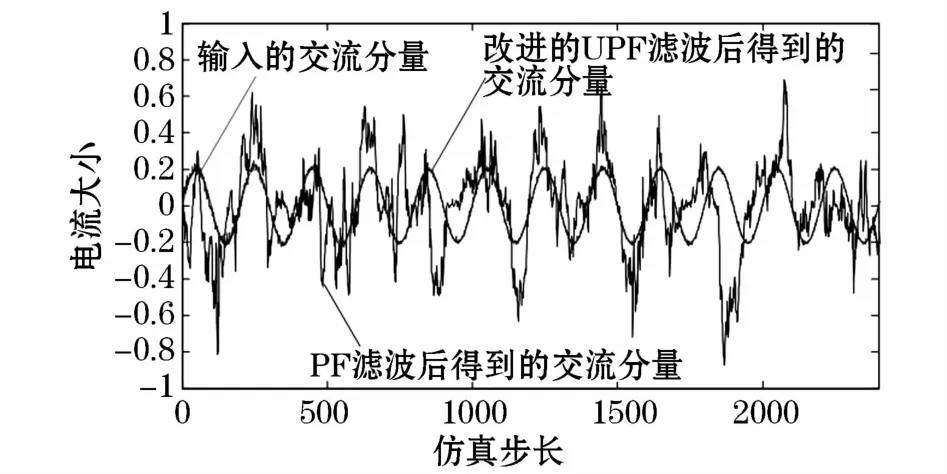
图2 滤波后交流分量波形Fig.2 Alternating current component waveform after filtering

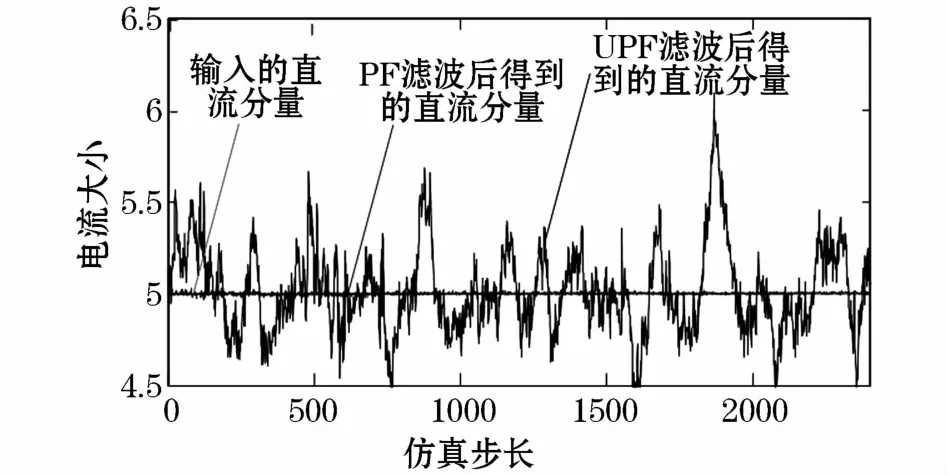
图3 滤波后直流分量波形Fig.3 Direct current component waveform after filtering

显然在低信噪比输入下，改进的UPF比PF有更好的信噪分离能力。

同时，将改进UPF算法与UPF进行比较，结果如图4、图5所示。

图4 滤波后交流分量波形Fig.4 Alternating current component waveform after filtering

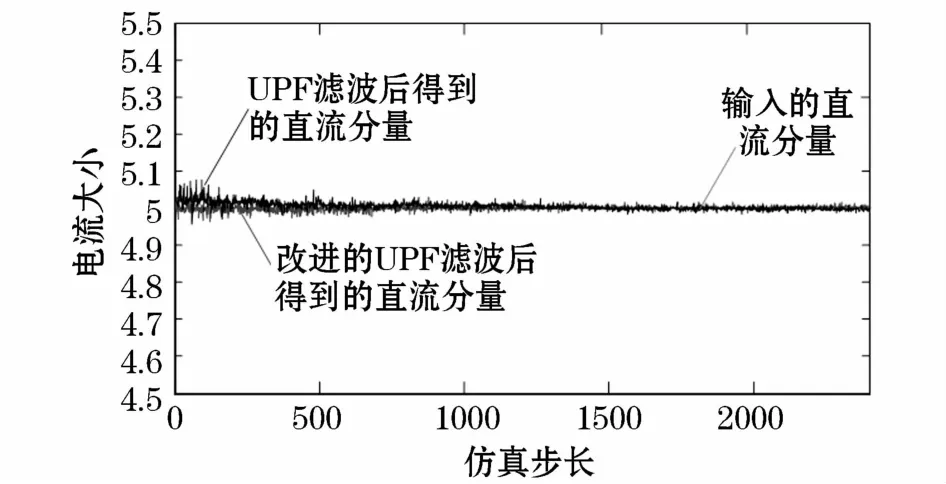
图5 滤波后直流分量波形Fig.5 Direct current component waveform after filtering

结果显示改进的UPF算法在提高计算速度的同时，在分离交直流分量的精度上与UPF相比并没有下降。

各算法的仿真时间和与输入电流的平均误差，如表1所示。

表1 各算法的仿真时间平均误差Tab.1 Average error of the simulation time of each algorithm

通过仿真图和表1可以得到：

（1）基于全局采样的UPF算法在低信噪比时，滤波的相对误差维持在0.002（0.2%）以内，仍能比较准确的实时滤波得到输入的交流量以及直流量，满足国家标准；

（2）在滤波的精度及所需时间上，改进UPF滤波算法比已有的粒子滤波和传统滤波都有较大提高。

4 三相短路故障时改进UPF信噪分离分析

当电力系统发生故障时，改进UPF滤波因短路电流与稳态电流相差极大，滤波得到的电流将存在很大误差。因此，需要在滤波中对系统是否发生短路进行判断，当短路故障发生后，改进UPF滤波应立即停止滤波直接输出采集的输入电流，之后当重合闸成功故障切除时，OCT应该重新开始滤波；当重合闸失败故障仍然存在时，继续输出采集的输入电流。

固改进UPF滤波要在发生三相短路故障时准确滤波，首先需要对系统发生三相短路进行准确判断，现将故障电流对滤波算法的影响进行说明。

对基于全局采样的改进UPF的OCT滤波算法第三步进行变换可得：

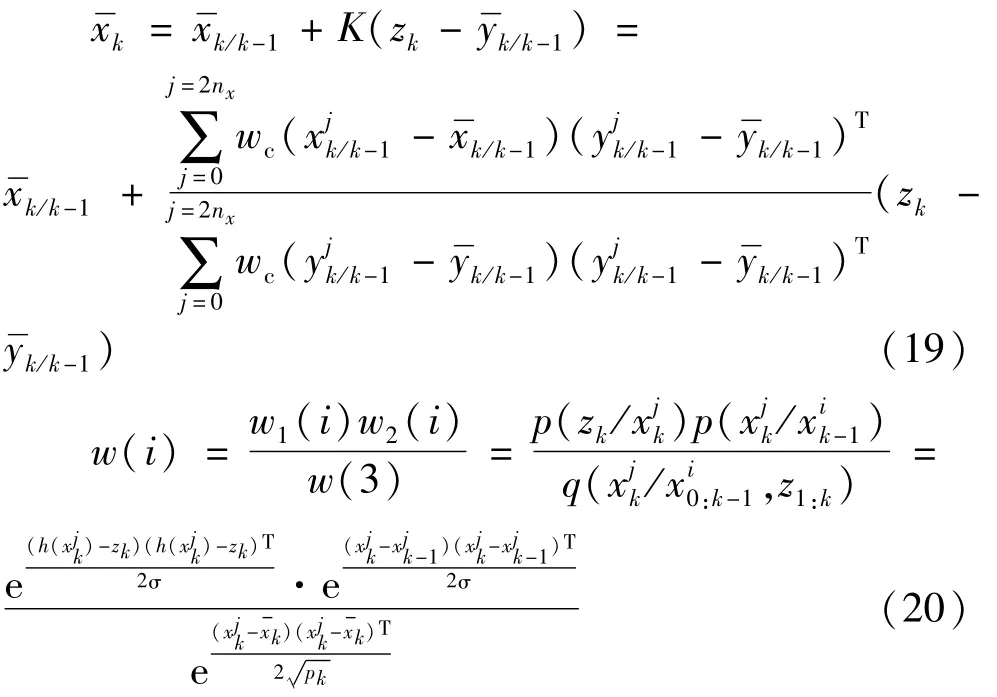
状态量x服从先验概率分布N（0，σ），且采样率为6 400 Hz，在高速采样中状态量变化极小，（aj－b）（h（aj）－得到的值很小约在［－1014，10－13］区间内，与权值 w（i）计算时引入得最新量侧值比较，式（5）中与 w1相比，w2、w3受最新观测值的影响较小，固w1（i）更能灵敏的反应量测值的变化。w1是稳态电流模型的似然函数概率值，当短路故障发生后，短路电流在短时间内急剧增加，残差值 err（t）＝y（t）－z（t）会变得很大，即电流预测值yk的值将落在可信区间外，导致w1（i）的值为0，所以通过设置阈值err，就能够实现对故障发生的判断。

短路发生后w1的残差值为err1随着故障电流的周期变化而变化如图6所示，若直接进行阈值判断因与稳态时的残差变化有交集，将引起对系统是否短路故障的错误判断。

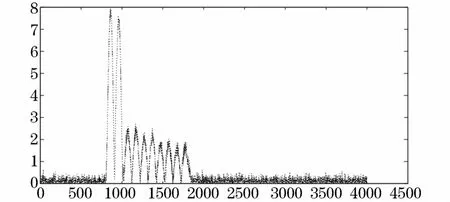
图6 权值w1的残差值Fig.6 Residual value of the weights w1

周期内err平均值变化如图7所示，能够对是否发生故障进行阈值判断，固本文以周期内err平均值作为阈值判断。

图7 固定周期内的残差平均值Fig.7 Fixed cycle of average residual error

Matlab-Simulink仿真平台搭建典型单机无穷大系统仿真三相短路故障，如图8所示。

图8 单机无穷大系统Fig.8 Single power infinite system

通过设置断路器的关断时间，与故障发生时间相配合，仿真断路器重合闸情况OCT输入电流为短路电流加上一个噪声幅值为0.5 A的高斯白噪声。

4.1 自动重合闸成功情况短路电流的信噪分离仿真分析

仿真设置为：在800 ms时发生短路故障，断路器在1 000 ms时动作断开线路，在1 800 ms时自动重合闸成功，继续运行到4 000 ms。

图9所示UPF的滤波结果在1 000 ms到1 800 ms时误差较大，是因为OCT直接输出了采集得到的电流信号，没有滤除噪声，用来保证保护设备的速动性。

图9 自动重合闸成功下对短路电流的信噪分离Fig.9 Under the automatic reclosing successful signal-noise separation of short circuit current

4.2 自动重合闸失败情况短路电流的信噪分离仿真分析

自动重合闸失败情况仿真设置为：在800 ms时发生短路故障，断路器在1 000 ms时动作断开线路，在1 800 ms时自动重合闸失败，继续运行到4 000 ms，仿真结果如图10所示。

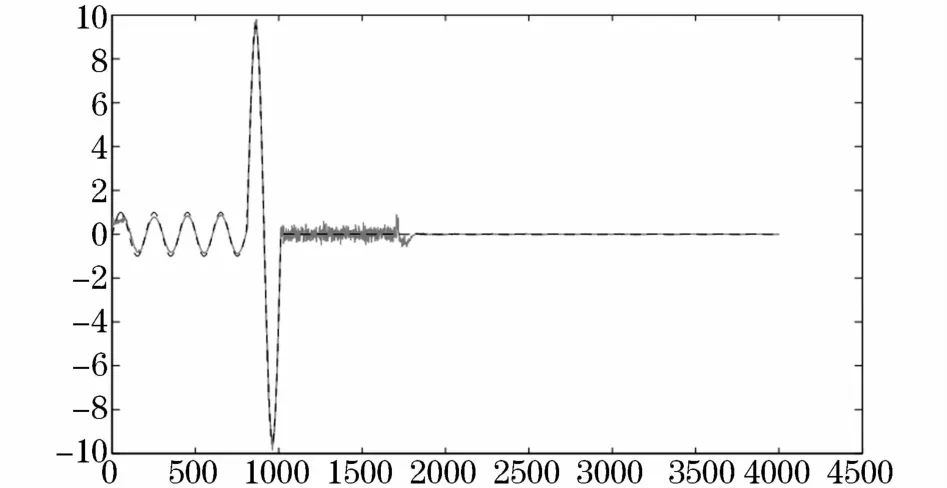
图10 自动重合闸失败下对短路电流的信噪分离Fig.10 Automatic reclosing failure under the signal-noise separation of short circuit current

仿真结果表明，针对单机无穷大系统发生三相短路时的短路电流，本文所提出的基于阈值的改进UPF滤波能够比较准确、及时的进行滤波，保证了保护设备的速动性、可靠性。

5 结束语

本文介绍了光学互感器的基本原理及信噪特性，为了在低信噪比输出下，提高滤波精度、准确分离出反映OCT温度变化信息的直流分量，提出基于全局采样的无迹粒子滤波方法来提高测量精度和计算速度，在低信噪比状态下提高了OCT信噪分离的能力。

系统的介绍了PF、UPF以及改进的UPF三种算法，并在matlab上对这三种方法稳态电流的滤波进行了比较，结果表明，对于光学互感器的含噪声输入信号，在分离交直流分量、实时滤波性能上，本文所采样的改进UPF明显优于PF和UPF，可以进一步应用于磁光式光学电流互感器的信号处理系统中。

针对含噪声的短路电流输入情况，本文在所提出的改进UPF滤波算法基础上进行了进一步改进，通过采用残差作为阈值，对系统是否发生故障进行判断，保证短路故障发生后OCT信号处理系统能够及时的、不失真的将输入电流提供给保护设备，在matlab上对单机无穷大系统发生三相短路进行了仿真，验证了三相短路时滤波的有效性，有效证明了改进UPF滤波应用的前景，下一步需要就不对称时的短路情况进行进一步的研究。