基于混合模型和交叉熵重要性抽样的发电系统可靠性评估*

王少伟，罗萍萍

（上海电力学院电气工程学院，上海200090）

0 引 言

可靠性指标作为现代电力系统的一个重要指标，其在电力系统的规划、运行、检修各方面都具有重要的意义［1-5］。目前在电力系统可靠性评估中应用最多的是蒙特卡洛法，为了提高蒙特卡洛法的计算效率，必须减小计算过程中可靠性指标的方差。因此，大量方差减小技术得到了广泛的研究与应用［6］。其中，用于电力系统可靠性评估中的方差减小技术主要有控制变量法［7-8］，对偶抽样法［9］，分层抽样法［10-12］，重要性抽样法［13-14］等。在这些方法中应用最多的是重要性抽样方法，而在重要性抽样方法中文献［15］提出的基于交叉熵的重要性抽样方法又因其良好的方差减小效果以及操作过程简单等优点得到了广泛的应用。该方法基于单一概率质量函数进行迭代抽样（称之为基于单一概率质量函数的交叉熵重要性抽样，Cross-Entropy based Importance Sampling with Single PMF，CEIS-S），在处理高可靠性电力系统时如果预抽样阶段的样本数较少，可能导致预抽样过程结束时得到的“最优概率质量函数”不能达到良好的方差减小效果，直接影响正式的可靠性指标计算阶段系统状态的合理抽取，从而降低可靠性指标计算效率，甚至可能得不到正确的结果，严重影响该方法的效率以及正确性为了克服这一缺点，本文结合混合概率质量函数模型和交叉熵原理［15-16］提出了基于混合概率质量函数和交叉熵重要抽样的发电系统可靠性评估方法（Cross-Entropy based Importance Sampling with mixture PMF，CEIS-M），可较大幅度提高发电系统可靠性评估的效率。

1 基于单一概率质量函数交叉熵的系统可靠性评估方法

交叉熵重要性抽样的基本思想是利用重要抽样法结合交叉熵操作，实现在保持原有样本期望值不变的条件下，改变现有样本空间的概率质量函数，使其方差减小，从而加快抽样仿真的收敛速度［15］，而交叉熵过程正是实现样本的概率质量函数修正的过程。

基于重要性抽样法的系统可靠性指标为：

式中 Ω为 C维系统状态空间，X=［x1，x2，…，xC］为由C个相互独立的伯努利变量组成的系统状态向量，对应系统中不同的元件。F（X）为系统状态X的可靠性函数，E（F（X））为系统可靠性指标。f（X；u）和g（X；v）分别为系统状态空间原有概率质量函数和修正概率质量函数且具有相同的形式，u=［u1，u2，…，uC］和 v=［v1，v2，…，vC］分别为 f（·）和g（·）的C维参数向量。以f（·）作为抽样函数时，变量xj以概率uj取值为0，表示对应元件处于故障状态；以概率1-uj取值为1，表示对应元件处于正常状态。以g（·）作为抽样函数时类似处理，衡量系统可靠性指标精度的方差系数为：

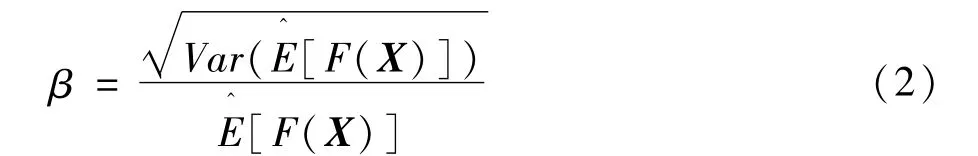
重要性抽样的效率与修正概率质量函数密切相关，为了寻求最优的修正概率质量函数{g（X；vopt）}，简记为 gopt（X），采用在函数族{g（X；v）}中通过确定最优参数向量vopt找到接近于gopt（X）的概率质量函数g′（X；v），当二者之间的距离足够小时将其视为的gopt（X）近似值，该距离采用Kullback-Leibler距离（即交叉熵）来衡量［15］，即：

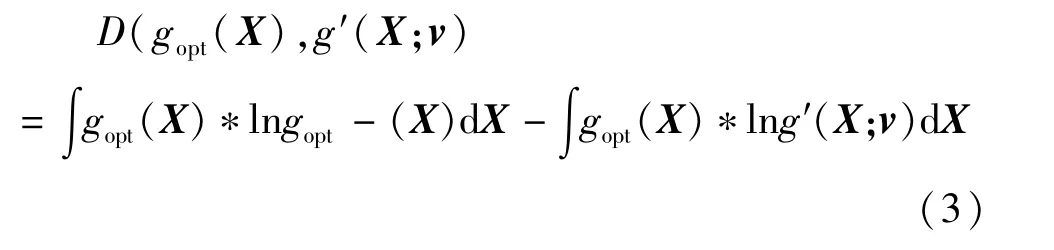
式（3）的最小化为如式（4）的优化问题：

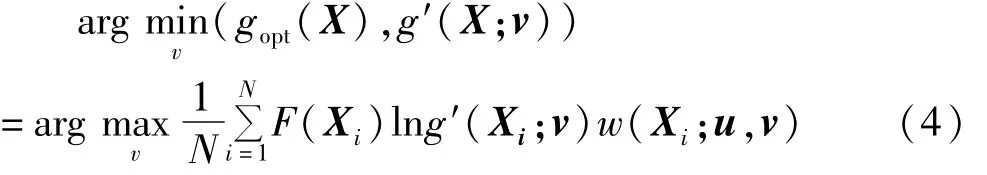
对于解式中的最小化问题，其最优解为：

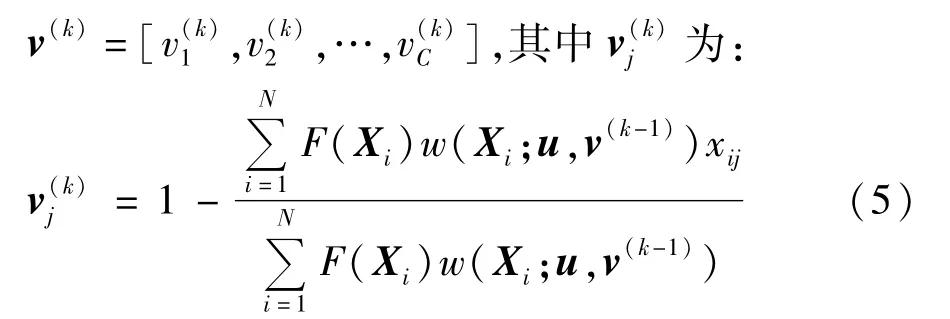
通过预抽样迭代即可求解式（5）并将迭代收敛时的中间分布对应的参数向量作为系统最优概率质量函数的参数向量 vopt=［vopt-1，vopt-2，…，vopt-C］并相应得到最优概率质量函数gopt（X）；然后即可根据gopt（X）进行正式抽样并由式（1）计算系统相应的可靠性指标，限于篇幅具体预抽样迭代求解过程及可靠性指标计算过程可参考文献［15］。

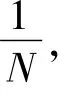
2 基于混合概率质量函数交叉熵的系统可靠性评估方法

2.1 混合概率质量函数模型

混合概率质量函数模型使用K个子概率质量函数的加权来描述系统的状态，系统的概率质量函数如下式：

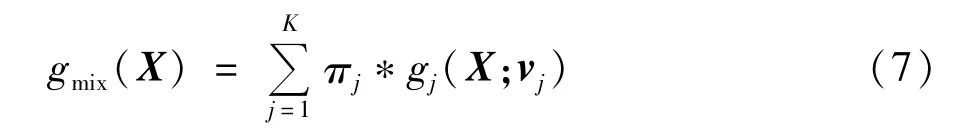
式中 gj（X；vj）（j=1，2，…，K）为与系统原始概率质量函数具有相同形式的子概率质量函数，πj为gj（X；vj）对应的权重。

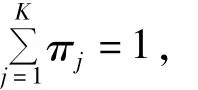
X服从每次由向量Z中取值为1的元素对应的某一概率子概率质量函数，因此，在给定Z时X的条件概率质量函数为：

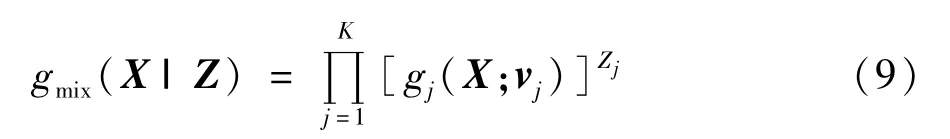
将式（8）乘上式（9）可得X和Z的联合概率质量函数如下式（10）：

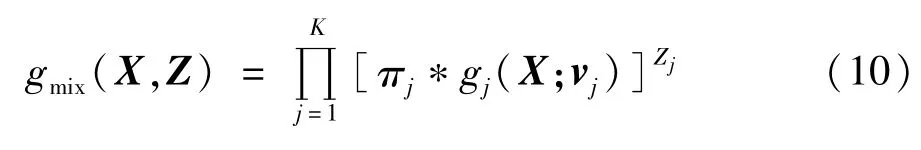
根据式（10）可求得X的边缘概率质量函数即混合概率值函数表的达式，如式（7）。

2.2 基于最小交叉熵原理的混合模型概率质量函数的更新

混合模型将gmix（X）作为描述系统状态的概率质量函数。在利用最小交叉熵原理对修正概率质量函数的参数进行更新时，基于单一概率质量函数交叉熵重要抽样的可靠性计算方法只对修正概率质量函数的参数向量进行更新，基于混合概率质量函数交叉熵重要抽样的可靠性计算方法同时对修正概率质量函数所包含的所有子概率质量函数的权值{π1，π2，…，πK}及其对应的参数向量{v1，v2，…，vK}进行更新。

将式（7）代入式（4），交叉熵最小化的问题转化为下式（11）：

式（11）中，Xi（i=1，2，……，N）是某一轮更新中根据概率质量函数gmix（X）抽样得到的样本，gimx（X）的参数 v1，v2，…，vK由上一轮更新得到，式（11）中，

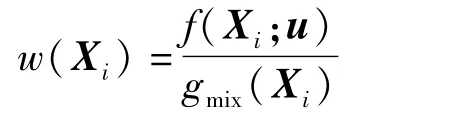
对于第j个子概率质量函数的参vj数的更新过程如下：

根据式（11）对 vj（j=1，2，…，K）求导可得：

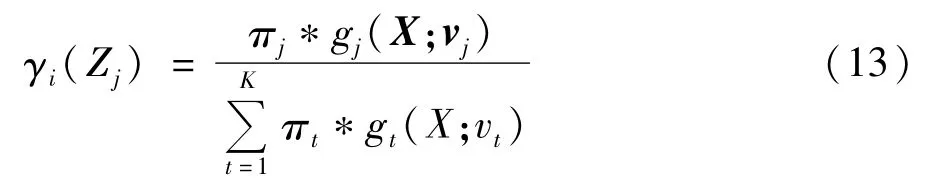
将式（13）代入式（12）可以得到vj更新的表达式如下：

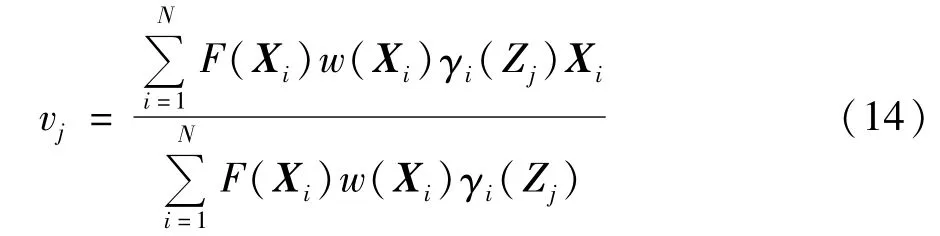
对于第 j（j=1，2，…，K）个子概率质量函数的权重πj的更新如下：

根据式（11）对πj求导可得πj的更新的表达式：

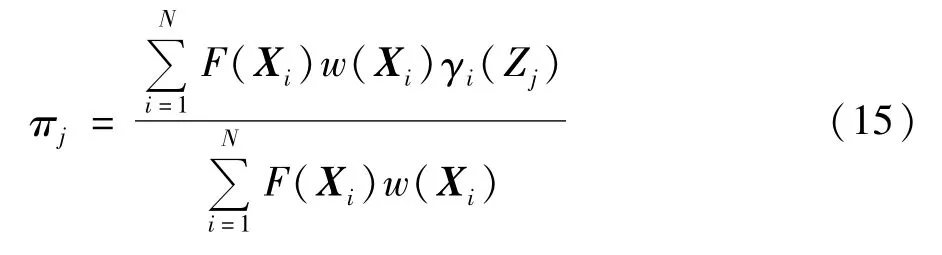
根据式（14）和式（15）即可完成对 vj和 πj迭代更新，直到式（11）中的最小化问题满足收敛条件时迭代停止，此时可得到最优的参数{vopt-1，vopt-2，…，vopt-K}和{πopt-1，πopt-2，…，πopt-K}，进而写出最后的最优概率质量函数gopt（X）如下：

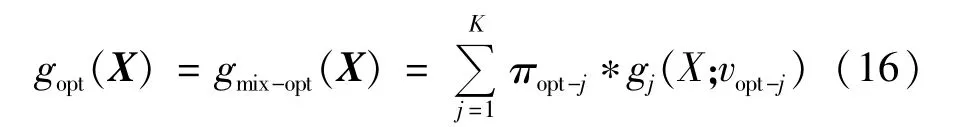
3 基于混合模型和交叉熵重要抽样的可靠性评估方法在发电系统中的应用

本文将CEIS-M方法应用于发电系统的可靠性计算中。设发电系统拥有C台独立运行的发电机，每台发电机只存在停运和正常两种状态，则各台发电机的状态可用伯努利变量表示，发电系统的状态可由向量X表示为 X=［x1，x2，…，xC］，其中 xj=1表示第j（1≤j≤C）台发电机处于正常状态，xj=0表示该发电机处于停运状态。系统负荷Ld取为其峰值负荷，故障标志为系统发电量S（X）小于Ld导致系统出现停电。基于本文CEIS-M法的发电系统可靠性指标计算共分两个阶段，具体过程如下：

阶段I：交叉熵预抽样求得最优混合概率质量函数。

该阶段包括8个步骤，步骤（1）和（2）为初始化过程，步骤（3）～（7）为基于交叉熵预抽样的混合概率质量函数参数更新过程，步骤（8）输出发电系统最优概率质量函数。

选用内置微处理器的低功耗网络继电器替换功耗较大的入侵报警主机。网络继电器具备开关量、干节点、继电器信号的输入/输出能力，可接入IP网络，具备自编程逻辑控制能力及远程操控能力，能够满足阀室的控制需求。网络继电器功耗在2 W左右，而报警主机的功耗在25 W左右，既满足了功能需求又降低了功耗。

（1）读入系统拓扑结构以及各发电机必要的数据信息，设定预抽样样本数为N，分位点ρ（一般在0.01～0.1之间取值），迭代次数以k表示：

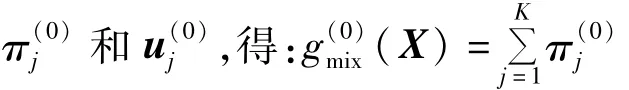
（4）记序列{S1，S2，…，SN}中的 S（1-ρ）N为 Lk，如果Lk≤Ld，令Lk=Ld。计算所有系统状态样本对应的失负荷概率指标（LOLP）的可靠性函数 FLOLP（X1），FLOLP（X2），…，FLOLP（XN）。对于 FLOLP（Xi），如果 S（Xi）＜Lk，令 FLOLP（X1）=1；反之，令 FLOLP（Xi）=0；

（5）计算所有系统状态样本的似然比函数，其中第i个系统状态样本的似然比函数 w（Xi；u，π，为，简记为 w（Xi）：

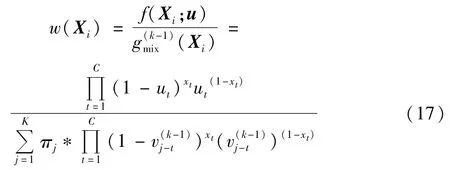
（6）利用第k次迭代抽取的系统状态样本X1，X2，…，XN，分别根据式（14）和式（15）更新第 j（j=1，2，…，K）个子概率质量函数对应的停运率向量及权重

（7）如果 Lk=Ld，迭代过程结束，转步骤（8）；否则 k=k+1，转步骤（3）；

阶段II：可靠性指标计算。该部分包括6个步骤，步骤（1）为初始化，步骤（2）～（5）为可靠性指标的计算，步骤（6）输出发电系统可靠性指标。

（1）设定发电系统可靠性指标的收敛标准为其方差系数β小于精度标准COV，COV一般取一个很小的正数，例如2%或1%；抽取NS（NS取1 000）个发电系统状态样本后在进行可靠性指标计算（避免在可靠性指标计算初期由于样本数量较少且样本对应可靠性函数相同（或相近）导致的可靠性指标出现过早的非正常收敛的情况）。样本数量初始值m=0；

（2）根据最优概率质量函数gopt（X）抽样得到发电系统状态，m++，Xm。若 m＜NS，转步骤（2），否则转步骤（3）；

（3）根据式（18）和式（19）更新计算可靠性指标及其对应的方差系数，并根据式（2）计算其对应的方差系数β。

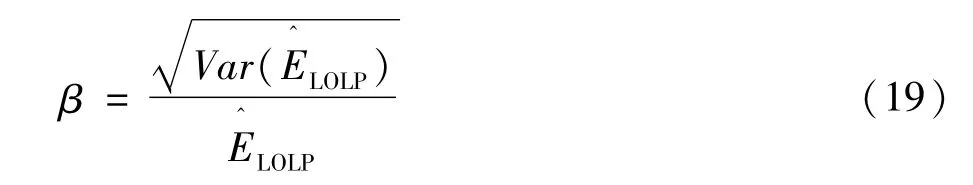
（4）若β＜COV，表示系统可靠性指标收敛，转步骤（6），否则，转步骤（5）；

（5）根据 gopt（X）抽样得到发电系统状态，m++，计算 FLOLP（Xm），以及 w（Xm），转步骤（3）；

（6）输出发电系统可靠性指标LOLP及其方差系数β。

在求解其他系统可靠性指标时只需要将系统可靠性函数F（X）相应值即可。例如求解系统缺供功率指标EPNS时，将系统可靠性函数F（X）取EPNS对应的值 FEPNS（X），若发电系统出现缺供则FEPNS（X）取相应的缺供功率的值，否则 FEPNS（X）=0。

基于CEIS-M法的发电系统可靠性分析流程如图1所示。

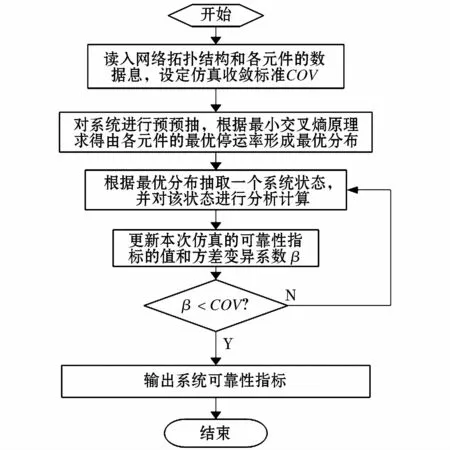
图1 基于CEIS-M的发电系统可靠性分析流程图Fig.1 Flow chart for generation system reliability evolution based on CEIS-M

3 算例分析

本文的算例对IEEE-RTS系统［17］的发电部分进行可靠性评估，该系统共32台发电机，装机容量3 405 MW，峰值负荷为2 850 MW，本算例的负荷水平按照峰值负荷考虑。分别利用基于CEIS-M法（本文方法）和文献［15］中基于CEIS-S法（方法1）以及原始蒙特卡洛法（方法2）分别对系统的发电部分进行可靠性评估，计算系统失负荷概率LOLP和电力不足期望值EPNS。

3.1 三种方法的收敛速度的比较

按照COV=2%的标准分别对三种方法进行单次仿真，然后比较三种方法对应的可靠性指标以及所需样本数和仿真时间。结果见表1。

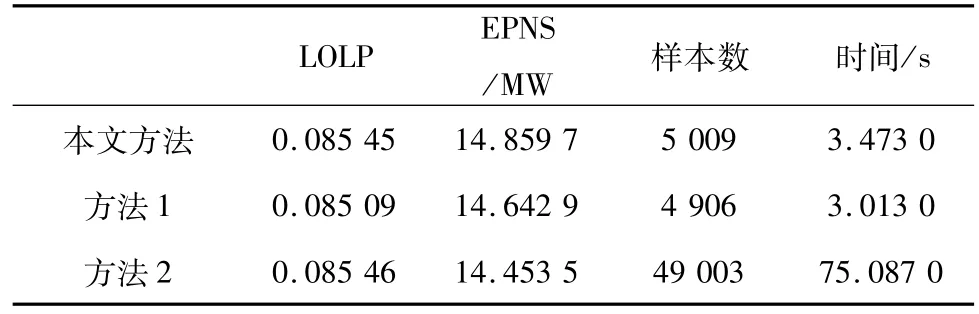
表1 三种方法的结果对比Tab.1 Results comparison of three kinds of methods

由表1可以看出，由于采用了基于交叉熵的重要性抽样方法，在相同的收敛标准下，本文方法和方法1的仿真速度和效率均远远高于基于原始蒙特卡洛法的方法2，并且三种方法得到的可靠性指标都满足准确性的要求。本文方法和方法1在仿真所需样本和耗费时间上并无明显差别。

3.2 处理高可靠性系统时本文方法和方法1的比较

在本算例中，将系统的负荷水平降低至20.5 MW的水平，得到修正的新系统。此时由于负荷水平降低，系统的可靠性必定会大幅提升，其可靠性指标LOLP和EPNS下降。算例对比了本文方法和方法1在处理修正系统时的预抽样阶段（阶段I）和最后的评估阶段（阶段II）中所需要的样本数以及仿真时间。其中，两种方法的收敛标准均为2%，本文方法中的子概率质量函数个数K取值20。表2和表3分别给出了两种方法每一轮预抽样中样本数不同时的相关仿真情况。

由表2和表3可以看出，两种方法在经过阶段I求得发电系统最优概率质量函数后，均能对发电系统可靠性指标进行有效的计算，两种方法的主要区别在于阶段I所需的样本数。方法1的阶段I每轮至少需要抽样130 000个样本才能对可靠性指标进行有效的评估，而本文方法的阶段I每轮只需要抽样50 000个样本即可对可靠性指标进行有效的评估。另外，对于两种方法而言，相应提高阶段I中每轮的样本数可以提高阶段2的可靠性指标评估效率，但是这也会大大增加阶段I所需的时间，使得整个评估过程效率降低。相比而言，本文方法在整个评估过程中所需的总样本数远远少于方法1在整个评估过程中的样本数，大大提高了其可靠性指标计算的速度。另外，考虑到对于发输电组合系统的可靠性进行评估时，每个系统状态样本都要利用最小切负荷策略进行负荷损失的计算，由于最小切负荷的优化问题非常耗时，本文中的评估方法由于所需样本较少其优势将会更加明显。

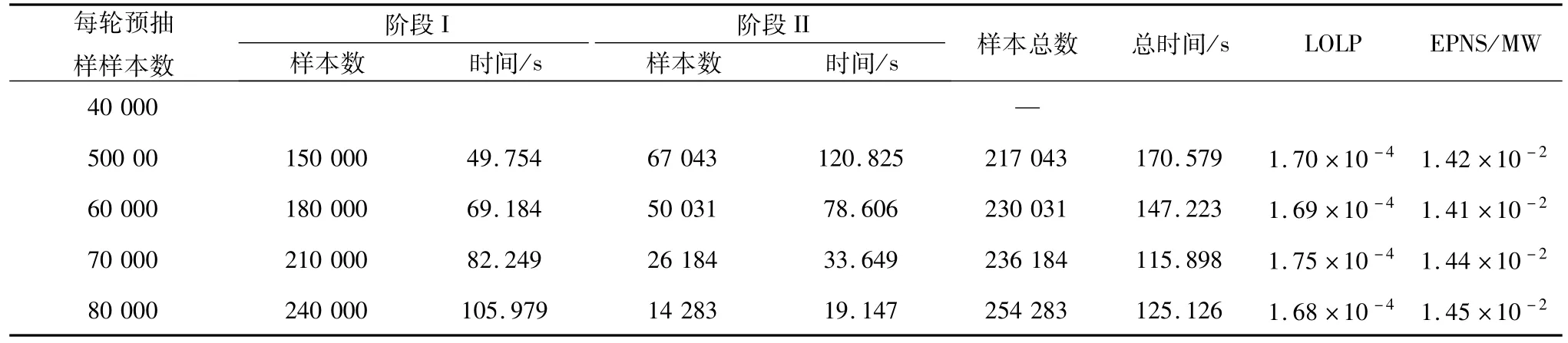
表2 本文方法的仿真结果Tab.2 Simulation results of the proposed method

表3 方法1的仿真结果Tab.3 Simulation results of the method 1

4 结束语

提出了一种基于混合模型和交叉熵重要性抽样相结合的发电系统可靠性评估新方法。该方法本利用多个子概率质量函数的加权来描述系统状态，克服了现有的基于单一概率质量函数交叉熵重要性抽样方法在处理高可靠性系统时其预抽样阶段需要抽样大量的样本从而导致可靠性指标总体计算效率降低的问题。算例结果表明本文方法在在处理高可靠性发电系统时，可在确保发电系统可靠性指标准确的同时使得预抽样阶段所需的样本数大幅度地减少，从而有效的加快整个可靠性评估过程，提高发电系统可靠性指标的整体计算效率。